空间目标的雷达定轨坐标转换问题
2020-08-25黄晓斌
黄晓斌, 张 燕, 肖 锐
(空军预警学院,武汉 430019)
0 引言
空间目标轨道确定是空间目标监视雷达的一项重要任务,主要的数据处理步骤(如图 1 所示)是:①坐标转换;②初轨确定;③轨道改进;④编目。在数据处理过程中,涉及到大量的天文学和数学知识。虽然国内外已有一些开源定轨软件可供借鉴,如 OrbFit[1]、ORSA[2]、NEOPROP[3]、Novas[4]、ODTBX[5]等,但这些软件都是针对天体轨道问题而研发的,且主要是处理光学观测数据,并不适合处理雷达观测数据。为此,本文开发了 1 套雷达定轨函数库(RadarOrbDet),能够有助于雷达技战指标的快速实现。RadarOrbDet 库按照上述4 个处理步骤开发,本文主要介绍其坐标转换模块。
本文通过讨论雷达定轨中涉及的基本坐标系、坐标转换的数学原理,给出程序设计思路,最后利用卫星工具包(satellite tool kit,STK)软件验证开发模块的有效性。

图1 雷达定轨数据处理流程
1 坐标系简介
雷达观测基于地球坐标系,空间目标轨道是基于天球坐标系,这就涉及到地球坐标系与天球坐标系之间的转换。
协议天球坐标系由国际天文学联合会(The International Astronomical Union, IAU)和国际地球自转和参考系服务组织(The International Earth Rotation and Reference Systems Service, IERS)发布,目前采用的是国际天球参考系(international celestial reference frame, ICRS)。依据坐标原点的不同,ICRS 可分为太阳系质心天球参考系(barycentric celestial reference system, BCRS)和地球质心天球参考系(geocentric celestial reference system, GCRS)。BCRS 用于计算行星的运动轨道及编制星表;GCRS用于计算卫星轨道及编制卫星星历。ICRS 由国际天球参考框架(international celestial reference frame,ICRF)来实现。在1997 年IAU 第23 届大会上,通过并决定自1998-01-01 起,在天文研究、空间探测、大地测量以及地球动力学等领域中采用ICRS[6]。
协议地球坐标系由国际地球参考系(international terrestrial reference system, ITRS)实现。GCRS 是1 个相当好的准惯性系,卫星的轨道计算一般都是在 GCRS 中进行。这就必须涉及到GCRS 与ITRS 间的坐标转换问题[7]。
2 坐标转换原理
在雷达定轨中,需要将在站心地平坐标系下的雷达观测数据转换到GCRS 坐标系中。
2.1 站心地平坐标系Xh与ITRS 坐标系XGO的转换
站心地平坐标系Xh与 ITRS 坐标系XGO的定义如表1 所示。

表1 站心地平坐标系与ITRS 坐标系的定义
站心地平坐标系与ITRS 坐标系之间的转换公式为

2.2 ITRS 与GCRS 坐标系的转换
ITRS 与GCRS 的转换早期是基于春分点的。目前,IERS 2010 年建议使用基于无旋转原点(nonrotating origin, NRO)的转换方法[9]。基于 IAU 2006/2000A-CIO 模型的转换流程[9]如图2 所示。
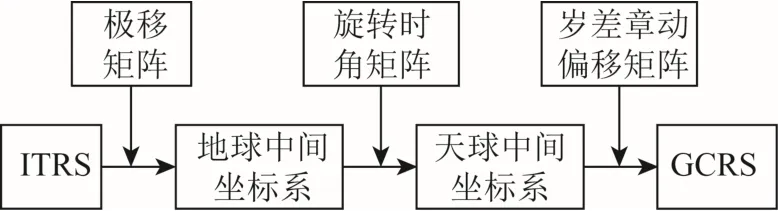
图2 “IAU 2006/2000A-CIO based”坐标转换流程
转换过程中涉及到2 个中间坐标系:地球中间坐标系(terrestrial intermediate reference system, TIRS)和天球中间坐标系(celestial intermediate reference system, TIRS)它们的定义见表2。

表2 TIRS 坐标系与CIRS 坐标系的定义
表 2 中:TIP(terrestrial intermediate pole)为地球瞬时自转轴;TIO(terrestrial intermediate origin)为地球中间零点;CIP(celestial intermediate pole)为天球瞬时自转轴;CIO(celestial intermediate origin)为天球中间零点。
在t时刻,ITRS 和 GCRS 的转换是 2 个 3 维直角坐标系间的转换,可以写成

式中:M(t)、RCIO(t)和W(t)分别是由于 CIP 在 GCRS中的运动(岁差章动)、地球的自转以及 CIP 在ITRS 中的运动(极移)引起的旋转矩阵。它们的具体表达式见文献[9]。
3 程序设计
图3 给出了坐标转换的程序设计流程图,其转换过程分为 3 个部分:①将目标在测站地平坐标系的极坐标转换为ITRS 坐标系下的直角坐标;②根据转换时刻以及地球定向参数(Earth orientation parameters,EOP)数据形成 ITRS 到 GCRS 的转换矩阵;③将转换矩阵与ITRS 下的直角坐标相乘得到GCRS 下的直角坐标。转换流程中涉及一些时间系统的转换可参见文献[7]。图3 中的“TT 时间”表示地球时(Terrestrial Time)。

图3 坐标转换程序设计流程
在转换过程中有如下几个问题应该注意:
1)按照式(1)的要求,应该输入站点的天文经纬度和地理经纬度。前者用来进行坐标旋转,后者用来计算站点的大地直角坐标。但通常只给出站点的地理经纬度,在进行坐标旋转时,用地理经纬度替代天文经纬度,2 者虽有细微的差别,但在绝大多数场合可忽略不计,如果需要极高坐标转换精度时应加以区分。
2)转换过程中需要地球定向参数(Earth orientation parameters, EOP)数据,它可从网站下载获得[10],要注意表中数据的有效时段和数据条目的时间间隔(通常为1 d)。因此,在给定转换时刻时,通常需要依据该表插值来获取更为精确的数据,而当转换时刻超出EOP 数据表有效时间范围时,一般可取最接近该转换时刻的数据来替代,但当超出时间范围间隔过大时,其误差应加以考虑。
3)当需要极高坐标转换精度时,在用EOP 数据表插值计算极移和世界协调时(coordinated universal time,UTC)与 1 类世界时(universal time,UT1)参数时,需要额外考虑海潮和固体潮的修正[7],但同时会导致转换速度的下降。
4 软件接口调用及有效性验证
4.1 接口调用示例
RadarOrbDet 库坐标转换功能的使用方法如下:
步骤①:打开VS2015,新建控制台应用程序,并命名为 radarorddet_Test,输出模式设为 64 位Debug,具体方法可参考文献[11]。
步骤②:从百度网盘下载RadarOrbDet 开发包[12],并拷贝到工程目录中,如图4 所示。
图4 测试工程目录结构
步骤③:在radarorbdet_Test.cpp 文件中输入如图5 所示的代码。

图5 函数接口调用示例
4.2 接口函数有效性验证
在 STK 11.2 版中仿真 1 颗卫星,其轨道参数设置如图 6 所示,测站位置参数设置如图 7所示。

图6 卫星轨道参数设置

图7 测站位置参数设置
仿真时间段设在2016-09-15 UTCG(格林尼治协调世界时) 04:00:00 至 2016-09-16 UTCG 04:00:00(STK 没有最新的EOP 数据,故设此时间段保证STK 自带的EOP 数据有效)。利用STK 的报表功能输出测站对卫星的观测时刻、观测距离、方位和俯仰数据,同时输出STK 内部计算所得的卫星GCRS 坐标,坐标数据的采样时间段为2016-09-15 UTCG04:00:00 至 2016-09-15UTCG 04:02:00,间隔1 s,总共121 点数据,图8(a)显示了距离测量数据,图8(b)显示了方位测量数据,图8(c)显示了俯仰测量数据。
利用 RadarOrbDet 软件包计算 GCRS 坐标(XROD,YROD,ZROD),采用式(3)描述的 GCRS 坐标相对误差与STK 的输出进行比较,图9 显示了相对误差曲线(实线)。从图9 中可以看出相对误差在 1×10-7水平,经分析表明,误差的主要原因是STK 报表以文本方式输出数据,导致数据产生精度截断误差,由此可知软件包算法是有效的。此外,在图9 中还绘制了俯仰角曲线(虚线),可以看出当俯仰角越小时,转换的误差越大,其原因是俯仰角越小时,截断误差对坐标转换误差的影响越大。
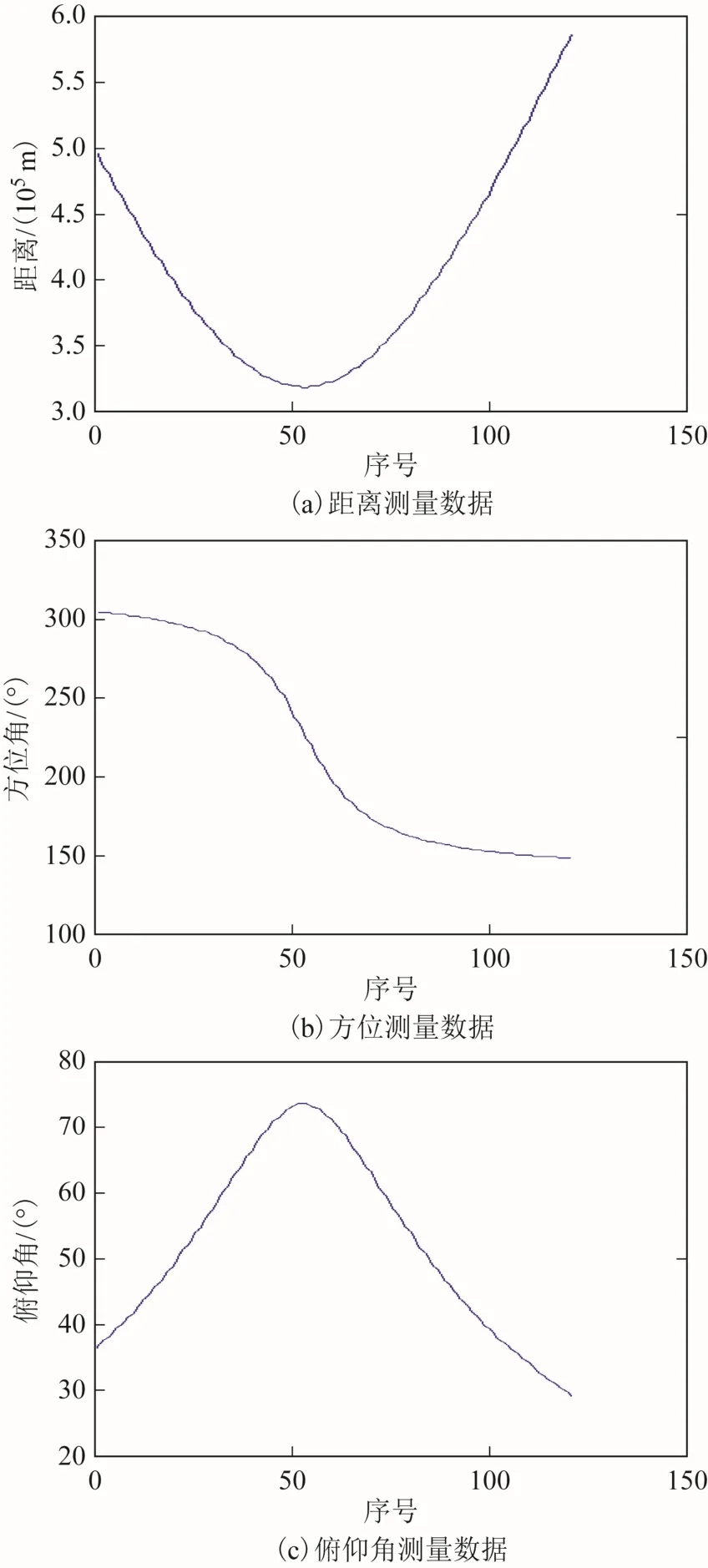
图8 测站观测的距离、方位和俯仰数据
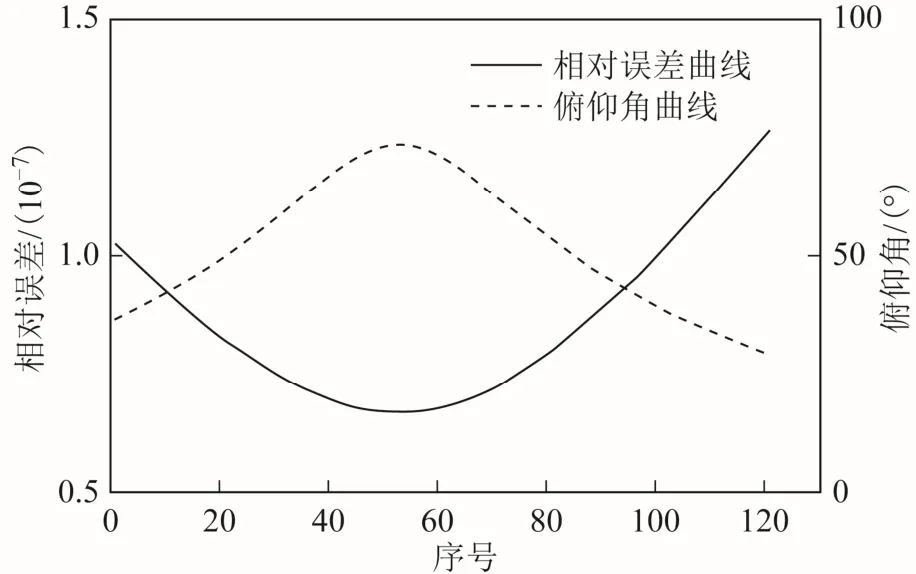
图9 GCRS 坐标转换相对误差

5 结束语
本文介绍了 RadarOrbDet 库中坐标转换模块的基本数学原理,给出了程序设计思路,描述了调用方法,最后用STK 验证了算法的有效性。下一步将继续介绍初轨确定模块的功能。
