线性正则化函数Logistic模型

孟银凤 梁吉业

1(山西大学数学科学学院 太原 030006)2(计算智能与中文信息处理教育部重点实验室(山西大学) 太原 030006)(mengyf@sxu.edu.cn)

在大数据时代，随着互联网、物联网、三网融合、云计算和其他高新通讯技术的发展，系统的运行过程被及时、快速、高频地记录下来[1-2].许多过程数据具有动态、连续的特征[3-4]，比如金融领域的股票数据、医疗领域的心电图数据、气象领域的气温数据等，这些都称为函数型数据.由于函数型数据广泛存在于各个领域，所以从这类数据当中发掘有用的知识具有重要的科学意义.

在函数型数据的挖掘任务当中，有许多有关函数型数据的分类问题.例如依据一个人的心电图曲线判断该人是否心律不齐；根据大理石的光谱曲线对其划分等级[5].本质上，每条函数曲线是函数空间的一个元素，应视为一个整体[6-7]，但在实践当中是离散采集的观测序列，因此，这个离散序列需要被转化为函数曲线，而这也成为函数型数据独特的数据预处理方式.基函数展开技术为将离散序列转化为函数提供了方法[8-9].受欢迎的基函数有Fourier基[5,10-11]和小波基[12-15].其他基函数有B样条[16-21]、Mercer核变换[22]和径向基[23-25]等.不同于前面提到的基函数，函数主成分基是一种数据驱动的正交基[26-32].

本文主要考虑函数型数据的二分类问题，基于函数主成分基建立线性正则化Logistic模型[28,33-35]，以实现更优的泛化性能.为此，借用精确度(Accuracy)、查准率(Precision)、查全率(Recall)、F1度量和Auc值5个指标刻画分类性能[36-37].

本文的主要贡献包括3个方面:

1) 提出了线性正则化函数Logistic模型，该模型在处理函数型数据的分类任务时既考虑了函数型数据的分类性能也考虑了模型的复杂度.

2) 给出的线性正则化Logistic模型限制了正则化子的取值范围，可依据交叉验证的方法在给定范围内选出一个经验最优正则化子.

3) 基于选出的正则化子，可以得到不同基个数下的正则化Logistic模型.

实验表明：当至少用10个主成分基函数去表示函数型数据时，其对应的线性正则化Logistic模型优于经典函数Logistic模型的分类性能，提升了函数型数据分类的泛化性能.

1 相关工作

本文面向函数型数据的分类问题，在对函数型数据进行主成分表示的基础上，给出了线性正则化函数Logistic模型，该模型限制了正则化子的取值范围，通过交叉验证便于选出较优的正则化子用于指导分类模型的选择，有利于选出泛化性能较好的模型.

2 函数主成分分析

函数主成分分析为将离散采集的数据序列转化为函数提供了一种数据驱动的方法.本节将介绍函数主成分基的获取方法.

2.1 函数主成分基

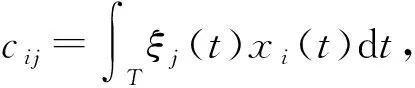
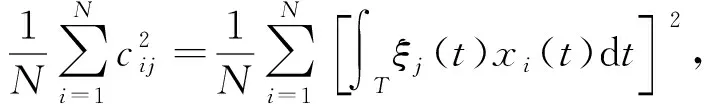
j=1,2,…,k.

(1)

由于ξj(t),j=1,2,…,k是标准正交基，考虑约束条件:

(2)

通过解约束优化问题，可得特征方程[6]:

(3)

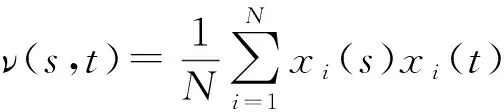
介绍一种求解特征方程式(3)的数值计算方法.首先通过其他基函数(如Fourier基、样条基等)将离散观测的数据序列转化为平滑函数，然后提取n个观测点s1,s2,…,sn处的函数值.令ω=|T|/n，这样，式(3)的左边可变为

(4)

记ξj(sm)=ξjm,m=1,2,…,n,j=1,2,…,k，由式(4)，式(3)可被数值表示为

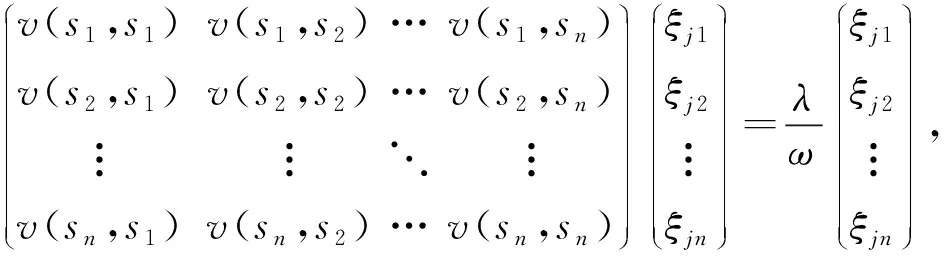
(5)

这样，通过解特征方程式(5)可得第j个主成分基ξj(t)的离散序列{ξj1,ξj2,…,ξjn}，然后通过平滑技术得到ξj(t).最后，根据

(6)

计算出第i个函数样例在前k个主成分的得分向量(ci1,ci2,…,cik)T，于是，该函数样例的主成分表示为

(7)

具体地，式(6)的计算可采用如下的数值计算法.基于xi(t)在n个观测点s1,s2,…,sn处的函数值xi(s1),xi(s2),…,xi(sn)和ξj(t)的离散序列{ξj1,ξj2,…,ξjn}，拟合得到：

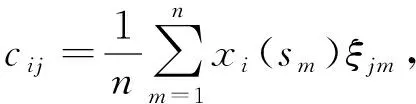
i=1,2,…,N,j=1,2,…,k.

(8)

2.2 主成分分析实例

以Tecator数据集(1)http: //lib.stat.cmu.edu /datasets /tecator为例展示函数主成分基的求解过程.该数据集由215条肉样本的近红外吸收谱曲线构成，其中有138块肉样的脂肪含量Fat低于20%.每条吸收谱曲线在波长850～1 050 nm的范围观测了100个通道.基于其二阶差分曲线如图1所示，进行函数主成分分析，其相应的协方差函数v(s,t)如图2所示.本文给出该数据集的前3个主成分基函数(principal component function, pcf)，如图3所示，其前3个主成分已提取超过85%的信息.

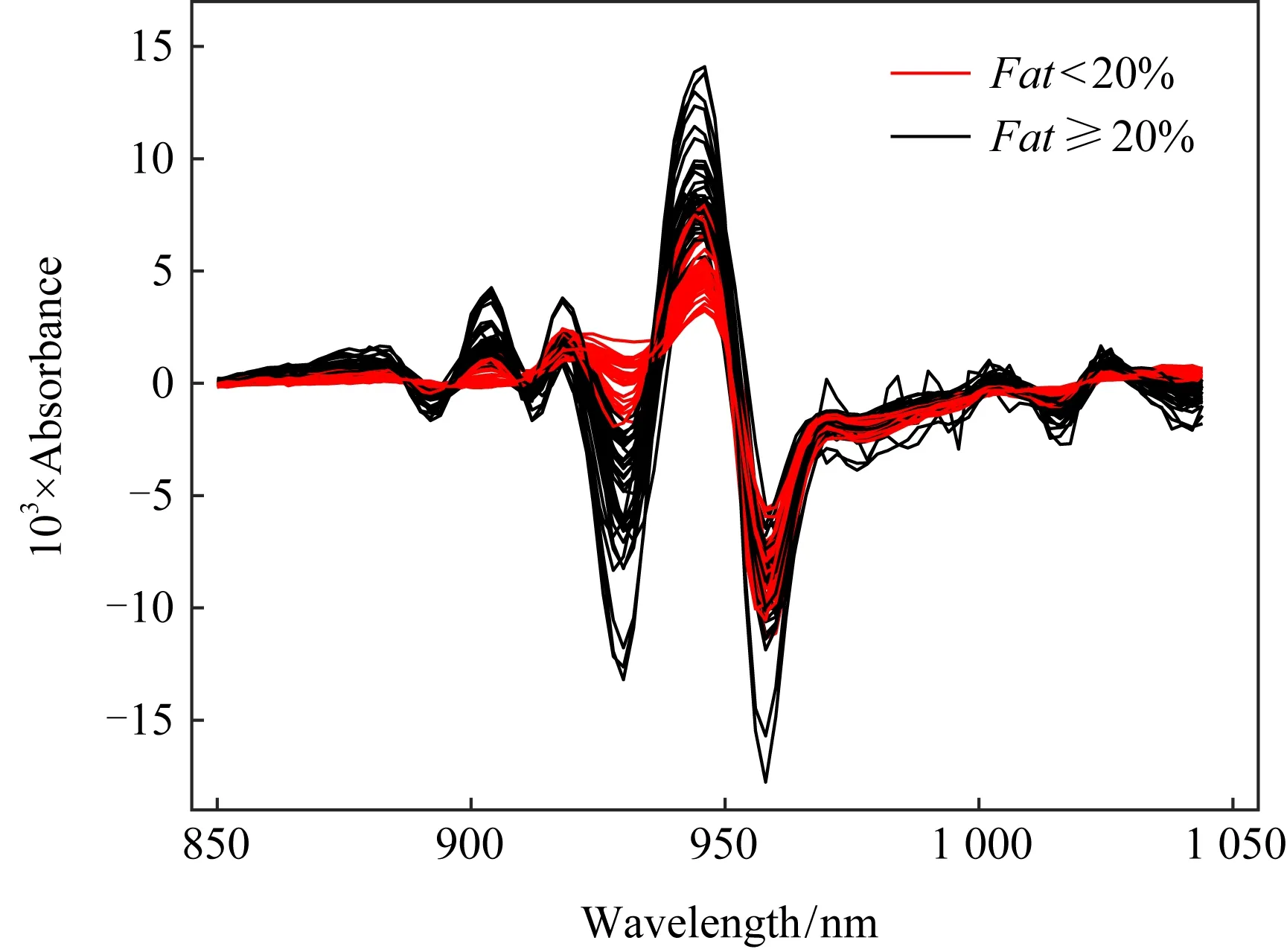
Fig. 1 The second differential curves of Tecator data图1 Tecator数据集的二阶差分曲线

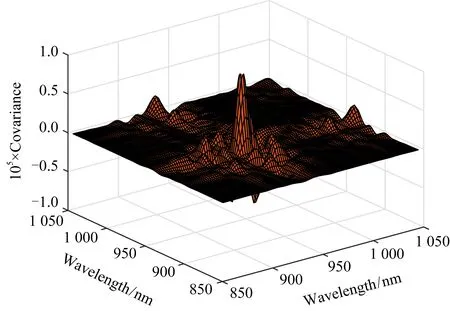
Fig. 2 The covariance function of Tecator data图2 Tecator数据集的协方差函数

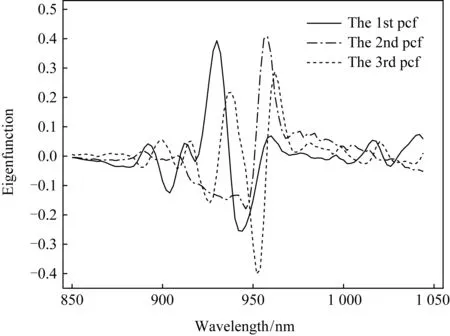
Fig. 3 The first three principal component functions of Tecator data图3 Tecator数据集的前3个主成分函数

图4给出了其前2个主成分的得分图.由图4可见，函数样例在第一主成分这一特征维上已具有很好的区分性.

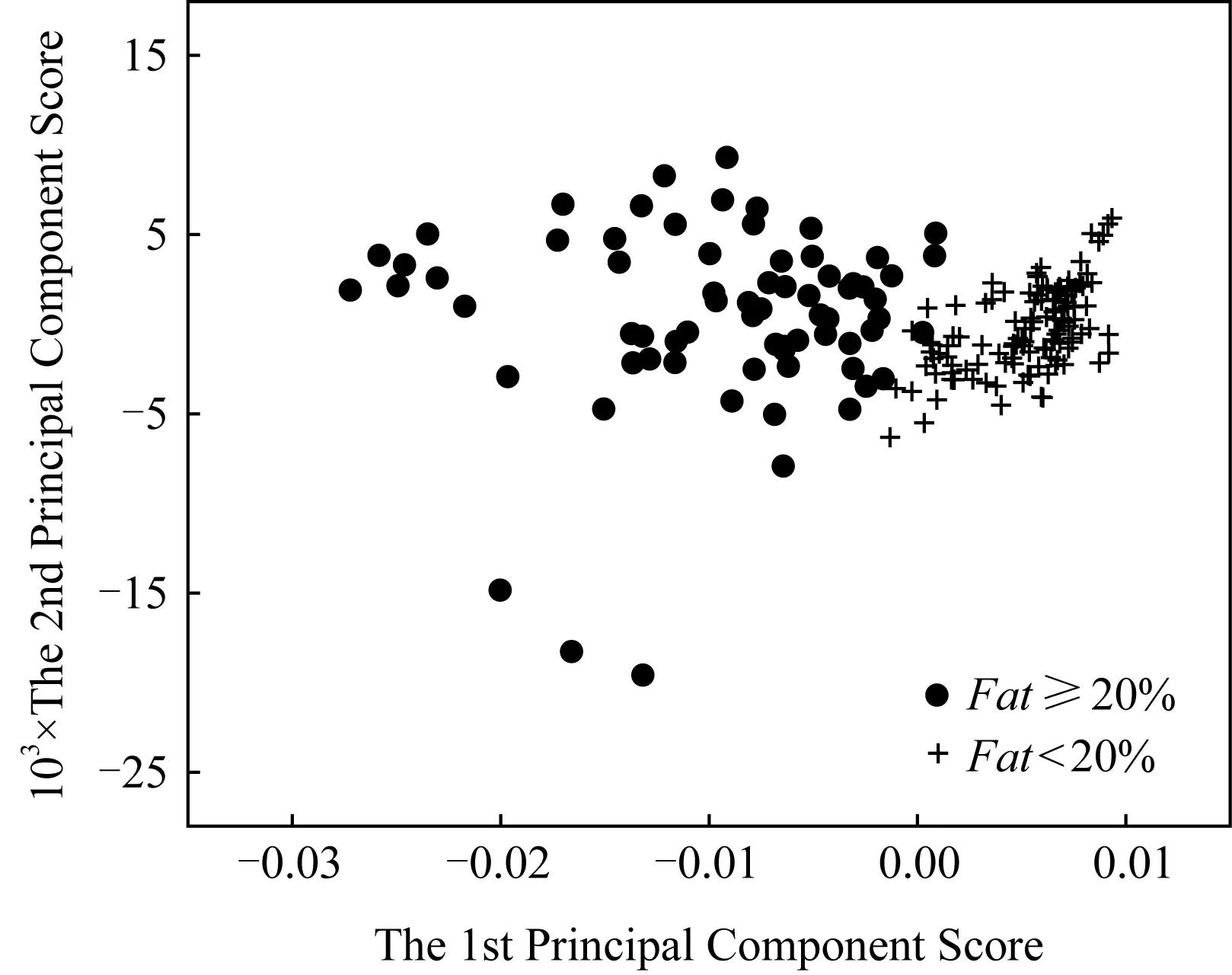
Fig. 4 The principal component scores of Tecator data图4 Tecator数据集的主成分得分图

3 函数Logistic模型

本节介绍经典函数Logistic模型及其求解方法.

3.1 函数二分类Logistic模型

(9)

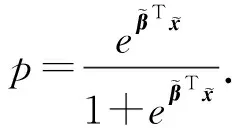
(10)

(11)

其中，α是参数，β(t)是参数函数.

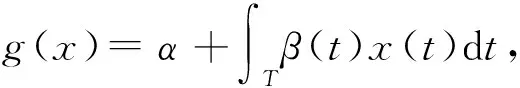
(12)

这里，式(11)或式(12)即为函数二分类Logistic模型.

3.2 函数Logistic模型的最大似然法

假定有N个函数样例x1(t),x2(t),…,xN(t)，其相应的类标签为y1,y2,…,yN.若这些函数样例相互独立，其联合分布即为边缘分布的乘积.因而，可得似然函数:

(13)

对x1(t),x2(t),…,xN(t)和β(t)进行主成分表示，其中x1(t),x2(t),…,xN(t)的表示结果见式(7)，β(t)的主成分表示为

(14)

由于主成分基ξ1(t),ξ2(t),…,ξk(t)是标准正交基函数，则

(15)

此时，式(13)取对数后变为

(16)

然后根据梯度下降法和拟牛顿迭代法得到参数的最大似然估计值.

4 线性正则化函数Logistic模型

本节在第3节的基础上给出线性正则化函数Logistic模型及其求解过程，并通过实例将其求解过程和经典Logistic模型比较.

4.1 模型提出及求解

为提高函数Logistic模型式(12)的泛化性能，在目标函数式(13)的基础上，我们构造出优化目标函数：

(17)

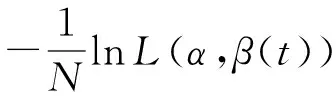
介绍优化函数式(17)的求解过程.同样，根据式(7)和式(14)，将函数样例和β(t)在函数主成分基生成的k维子空间进行低维表示，并记β=(β1,β2,…,βk)T，Xi=(ci1,ci2,…,cik)T.优化函数式(17)转化为

ln(1+eα+βTXi)]+(1-λ)βTβ},

(18)

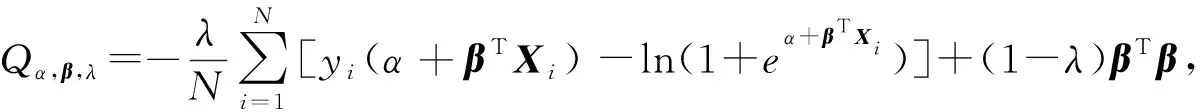
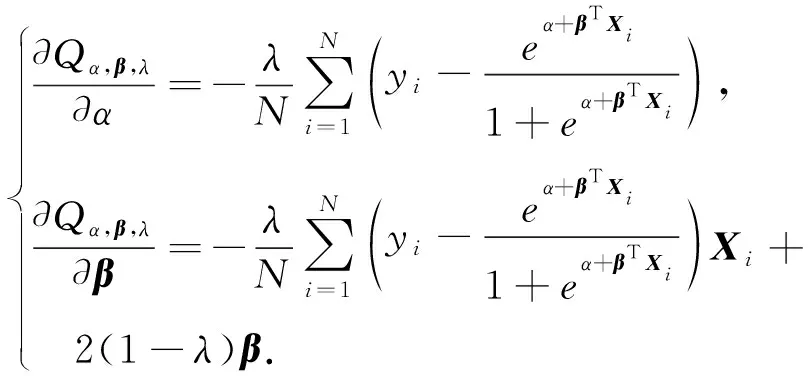
然后令导数为0，得非线性方程:

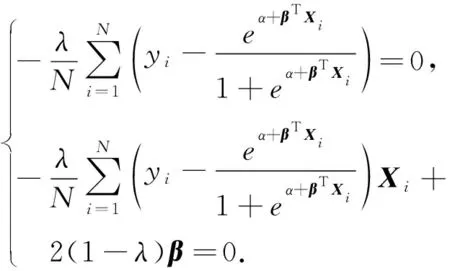
(19)

给出牛顿迭代法的求解过程.为此，计算：

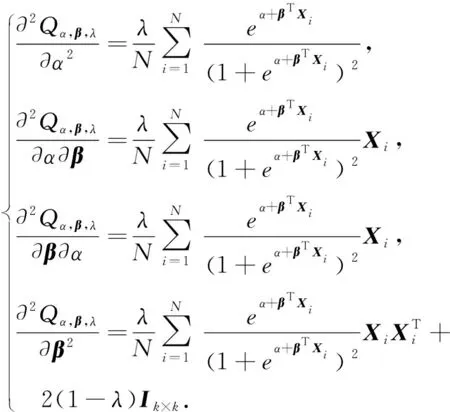
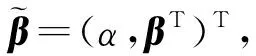
(20)

此时方程式(19)变为

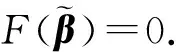
(21)

而

(22)

从而得到迭代公式:

(23)

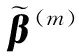
4.2 求解实例

本节仍以Tecator数据集为例探究线性正则化函数Logistic模型的求解过程，并将其与经典函数Logistic模型的优化过程对比，其对比结果见表1.在实验当中，我们采用前3个主成分基函数表示函数样例，因此，在2个Logistic模型中均涉及4个参数的求解，其中，λ=1对应经典函数Logistic模型，λ=0.9对应一个线性正则化函数Logistic模型.表1展示了2个模型的3轮迭代结果，通过表1，我们可以发现：1)正则化函数Logistic模型的迭代次数少于经典函数Logistic模型的迭代次数，因此，相较于后者，前者更能快速收敛；2)正则化函数Logistic模型的参数较小，而经典函数Logistic模型的参数较大，且相继的2次迭代间参数变化较大.对于参数λ取其他值时的线性正则化函数Logistic模型有类似于λ=0.9的结果，这里不再一一列出.因此，在增加正则化项的函数Logistic模型当中，由于其参数受到抑制使得模型更加稳健，从而限制了过拟合现象，为提升模型的泛化性能奠定了基础.

5 实验与结果

本节利用提出的线性正则化函数Logistic模型对函数型数据分类并测试该分类模型的泛化性能.为此，我们基于5个分类性能指标对包括Tecator数据集在内的6个函数型数据集进行了实验.

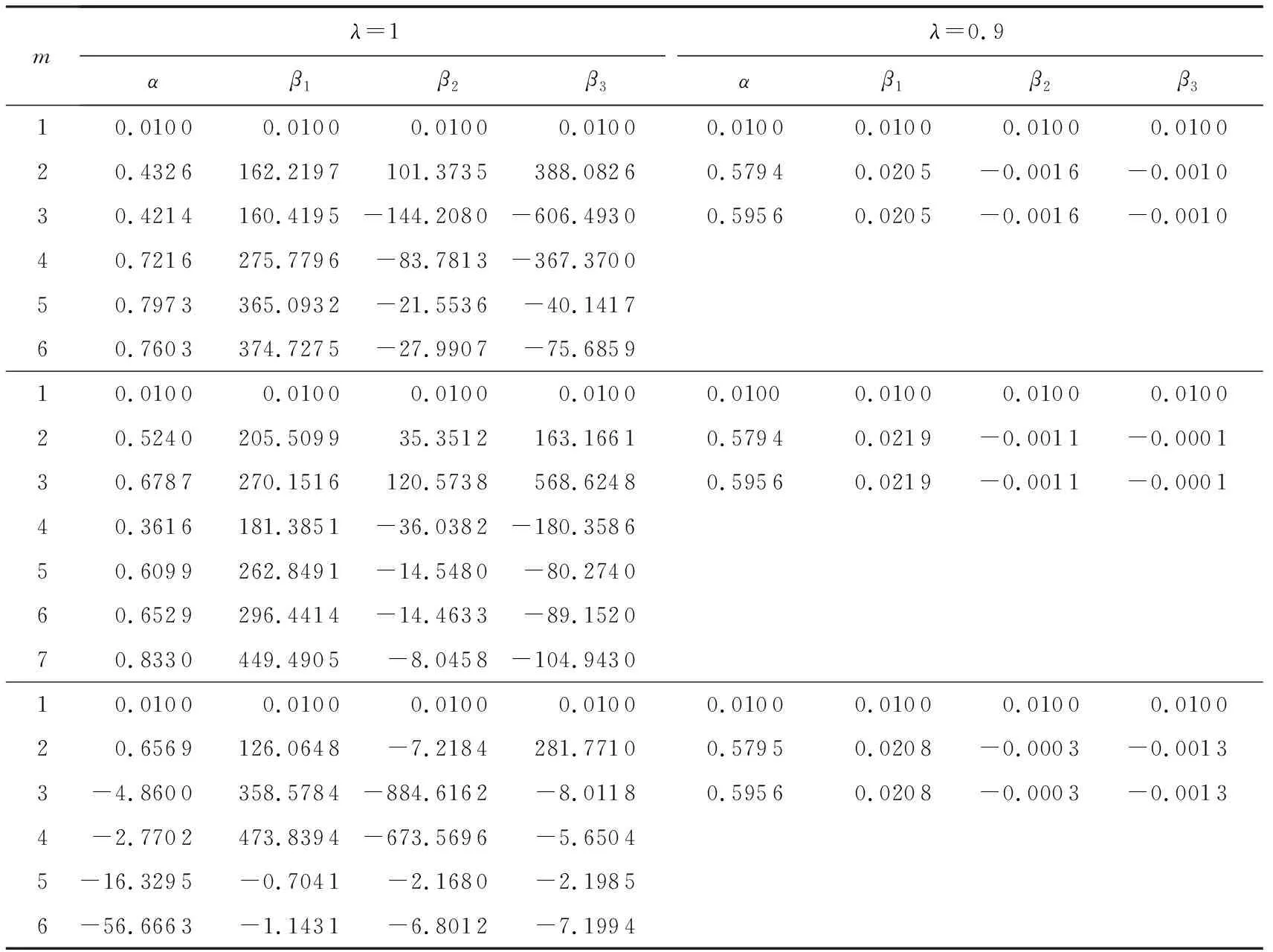
Table 1 The Iteration Process Comparison of Two Types of Logistic Models表1 两种Logistic模型的迭代过程比较

5.1 度量标准

对于二分类问题，根据测试集上样例的真实标签和分类器给出的预测标签可将样例分成4种状态[40]，这4种状态的样例数分别为TP(正类预测为正类的个数)、FN(正类预测为负类的个数)、FP(负类预测为正类的个数)、TN(负类预测为负类的个数).

根据上述样例数，可定义精度(Accuracy)、查准率(Precision)、查全率(Recall)、调和均值(F1)、灵敏度(Sensitivity)和特异度(Specificity)，具体定义为

(24)

(25)

(26)

(27)

(28)

(29)

另外，对于给定的阈值，可在二维平面上得到一个以灵敏度为纵坐标、特异度为横坐标的点.随着阈值的变化，会得到一系列点，这些点连成的曲线下的面积记为Auc值[47]，该值越大表明分类器的分类性能越好.

5.2 数据集

本文将在6个数据集上测试我们提出的方法.其中Tecator数据集在2.2节已介绍，下面介绍其他5个数据集的来源和构成.

Simudata数据集是一个人造数据集.该数据集如图5(a)所示，有2类，每类包含100个函数样例，每个样例等间隔地采集了101个观测点{t=1,1.2,1.4,…,21}[30].

第1类函数样例满足：

x(t)=Uh1(t)+(1-U)h2(t)+ε(t),

第2类函数样例满足：

x(t)=Uh1(t)+(1-U)h3(t)+ε(t),

其中，U是服从[0,1]上均匀分布的随机变量；ε(t)是白噪声过程，满足E[ε(t)]=0，Var[ε(t)]=1；h1(t)=max{6-|t-11|,0}，h2(t)=h1(t-4)和h3(t)=h1(t+4).

ECG数据集、Face数据集和CBF数据集均来自同一网址(2)http: //www.cs.ucr.edu /～eamonn /time_series_data/.ECG数据集如图5(b)所示，记录了2组患者的200条心电图数据，每条数据采集了96个观测点，一组有63个样例，另一组有137个样例.Face数据集如图5(c)所示，由56条曲线构成，每条曲线采集了350个观测点，该数据集包含2类：1)22个样例;2)34个样例.CBF数据集如图5(d)所示，包含620个函数样例，每个样例采集了128个观测点，每组各有310个函数样例.

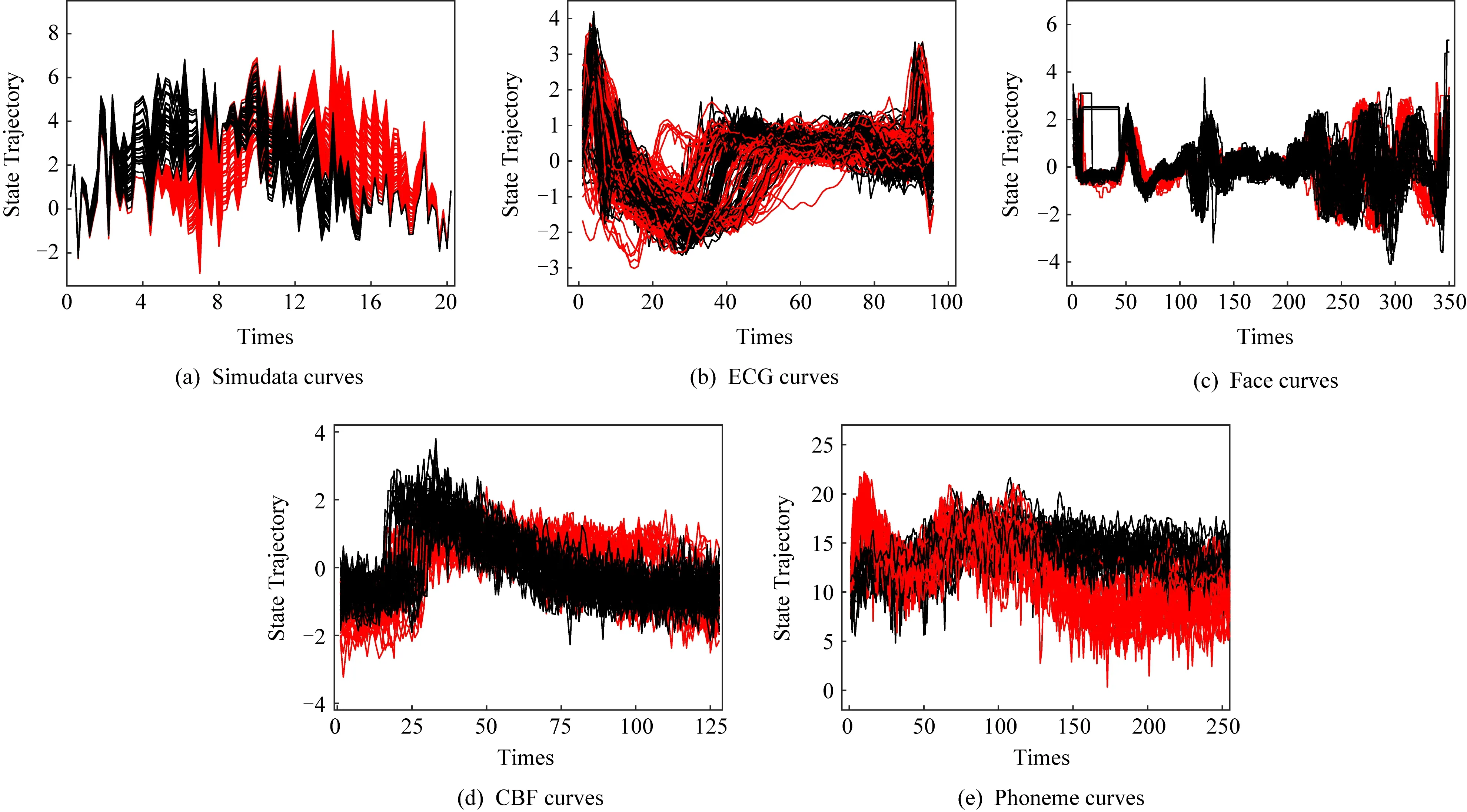
Fig. 5 Curve plots of various data sets图5 不同数据集的曲线图

Phoneme数据集来自TIMIT数据库[48]，该数据集如图5(e)所示，包含2 035个语音框架，其中有1 163个语音框架记录的是“she”中的元音的发音“iy”，872个语音框架记录的是“she”中“sh”的发音.每个语音框架采集了256个瞬时频率的对数周期图.

在图5(a)～(e)的各图中，红色曲线表示一类，黑色曲线表示另一类.

5.3 正则化子的选择

本节通过交叉验证的办法选择正则化子.由于本文给出的模型是线性正则化函数Logistic模型，而其中的正则化子λ∈[0,1]，因此，在给定范围内选择一个合适的正则化子相对应的模型是提高分类泛化性能的基础.

以CBF数据集为例给出正则化子参数的选择过程.分别选择函数主成分的贡献率达到85%,90%,95%,99%相对应的主成分个数，然后在基于这些个数的主成分表示下的线性正则化Logistic模型类中选出较优的λ对应的模型作为最终的分类模型.对每个贡献率要求下，参数λ在[0,1]等间隔地取100个点，每个参数取值下做了100次随机实验，得到分类性能指标Accuracy，Precision，Recall，F1和Auc的平均值.图6显示了随着参数λ的变化相应的线性正则化Logistic模型的分类精度，其中贡献率cum=85%时主成分个数k=19，当cum=90%时k=30，当cum=95%时k=47，当cum=99%时k=68.对于其他分类性能指标，有类似的曲线图.由图6可知，在不同贡献率下，选择不同个数的主成分基函数去表示模型，最终选出的最优参数λ是一致的，以下按照上述方法选出不同数据集对应的最优参数λ，其结果如表2所示：

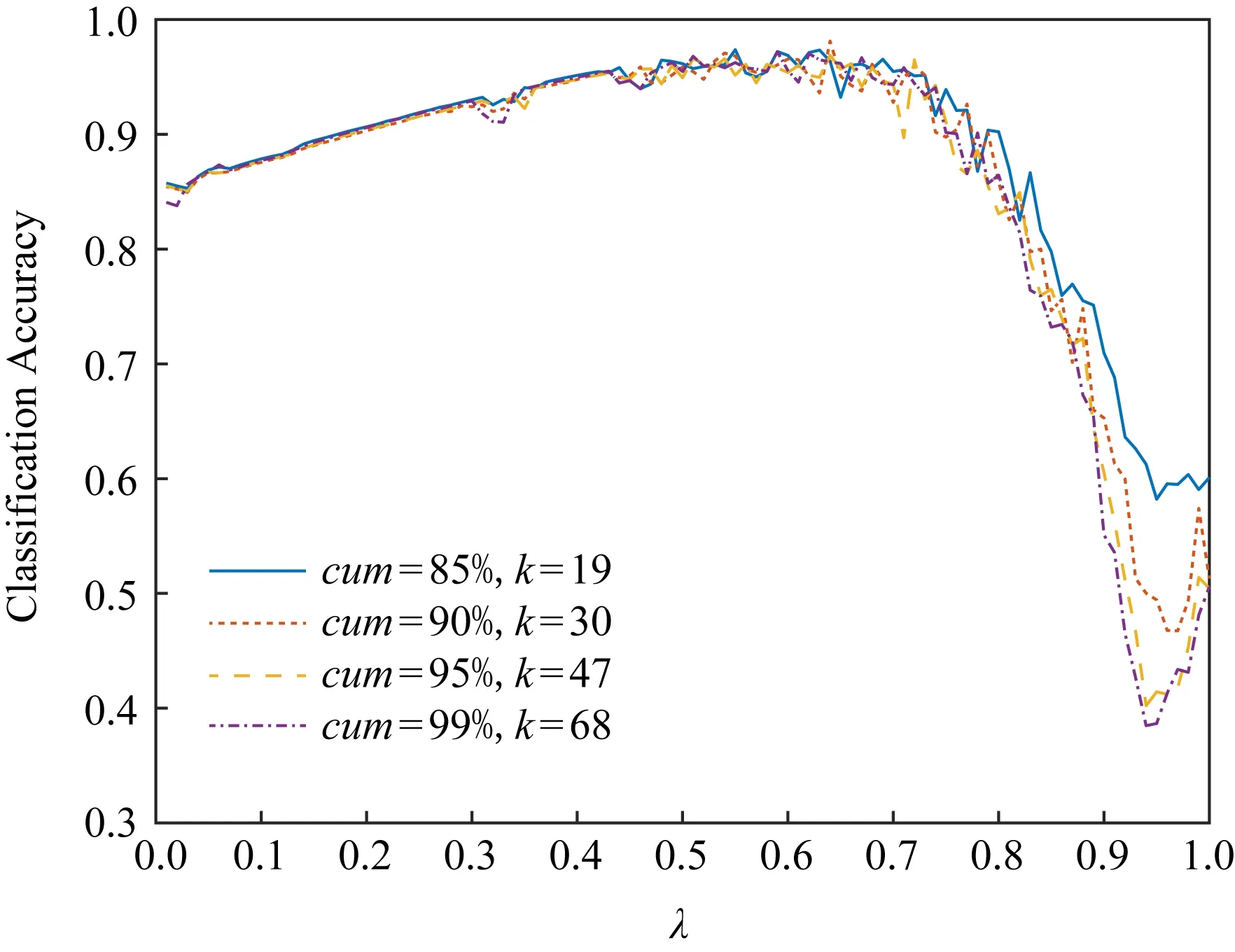
Fig. 6 Classification accuracy comparison for different number of basis functions图6 不同个数基函数的分类精度比较

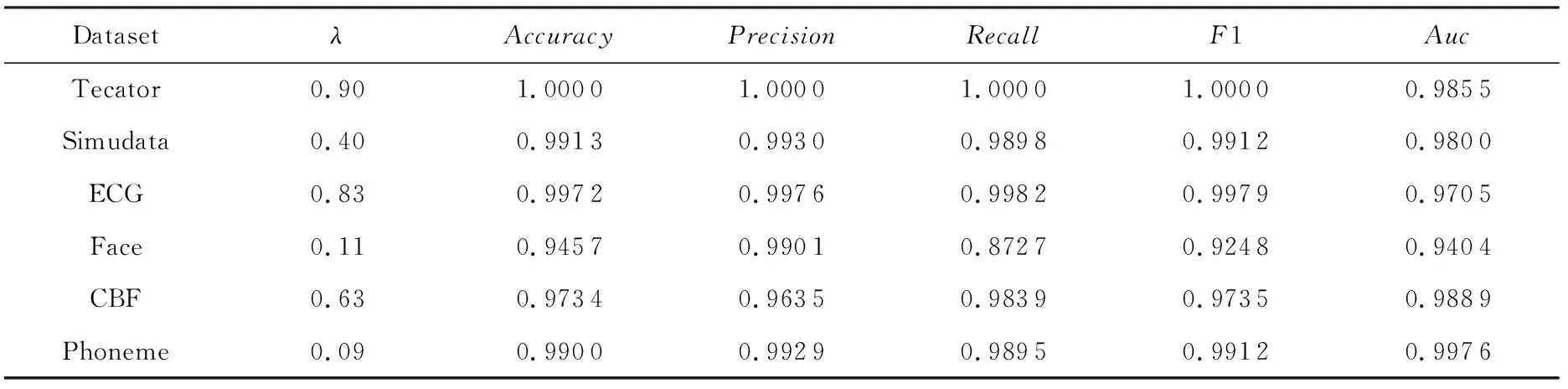
Table 2 Empirical Optimal λ and Classification Performance of Corresponding Linear Regularized Logistic Model表2 经验最优λ及相应线性正则化Logistic模型的分类性能

5.4 模型比较

对不同的数据集，我们将基于选出的最优经验正则化参数λ对应的不同主成分基个数下的线性正则化Logistic模型和经典函数Logistic模型进行比较，每个模型进行100次随机实验，经典函数Logistic模型的实验结果如图7(a)所示，本文给出的线性正则化Logistic模型的实验结果如图7(b)所示.

Fig. 7 Classification accuracy comparison of two types of logistic models图7 两种函数Logistic模型的分类精度比较

由图7(a)可以看到，在基个数较少时经典函数Logistic模型的分类性能较强，随着基函数数目的增加，相对应模型的分类性能在降低.由图7(b)可以发现，基个数较多时线性正则化函数Logistic模型的分类性能更强，随着基函数数目的增加，相应的分类模型的性能在提升.这是因为在样本容量固定的条件下，一般可以通过降维或正则化的方法提升模型的泛化性能.其中，经典函数Logistic模型是通过降维的办法来提升泛化性能，而这个低维子空间就是由前面少数几个主成分基函数生成的函数子空间；而线性正则化函数Logistic模型是通过正则化方法提升模型的泛化性能，也就是说通过减小模型的参数使模型更简单更稳健进而抑制过拟合.比较图7(a)和图7(b)，对于不同的数据集，当基个数取值大于10时对应的线性正则化函数Logistic模型的分类性能普遍优于经典函数Logistic模型的分类性能.

6 总 结

本文面向函数型数据的分类问题，提出了一种线性正则化函数Logistic模型.一方面，由于在该模型的构造中考虑了正则化项，所以能够提升模型的泛化性能；另一方面，由于采用了线性加权的方式构造了优化的目标函数，限制了参数λ的取值范围，方便找到一个经验最优参数值，可参考该经验最优值选出一个较优的Logistic模型，而这个模型通常优于经典的函数Logistic模型.