蒙德里安深度森林

贺一笑 庞 明 姜 远

(计算机软件新技术国家重点实验室(南京大学) 南京 210023)(软件新技术与产业化协同创新中心(南京大学) 南京 210023)(heyx@lamda.nju.edu.cn)

深度学习使得算法模型能够学得逐层抽象的数据表示[1].目前，大多数深度学习模型都是基于神经网络构建的，即可以通过反向传播训练的多层参数化可微模块[2].近年来，深度神经网络在与图像和语音相关的任务中取得了巨大的成功[3-5].

文献[2]认为，深度学习成功的关键在于逐层的处理、模型内的特征变换和足够的模型复杂度.由此提出了深度森林的一种具体实现gcForest[6]，它同时满足上述3个条件，而基于不可微的模块搭建，验证了深度学习不仅仅是深度神经网络.gcForest由决策树森林组成.和深度神经网络相比，它不依赖于反向传播进行训练，其模型复杂度可以根据训练数据自动确定，同时超参数少，而且对于不同超参数的设置和在不同的数据集上都有着稳健的性能表现.

考虑到在很多动态环境的实际应用中，会不断接收到新的训练样本，增量学习引起了广泛的关注[7-10].不过gcForest的训练过程要求所有训练数据预先给出，如果后续获得了新的训练数据，gcForest无法直接更新模型，而定期重新训练gcForest会带来昂贵的训练时间开销.因此我们希望设计可以增量训练的深度森林.

尽管蒙德里安森林有很多优点，但有2个问题阻碍了其性能的进一步提高.首先，蒙德里安森林始终基于原始特征进行学习，我们发现向森林中添加更多蒙德里安树并不是提高准确率的有效方法.其次，由于划分选择独立于样本标记，所以当无关特征较多时，蒙德里安森林会选择大量的无关特征用于划分，而导致其预测性能不理想.

本工作中，我们提出了蒙德里安深度森林(Mondrian deep forest，MDF)，它以一种级联的方式集成了蒙德里安森林，使其既有深度森林的预测准确性，又有蒙德里安森林增量学习的能力.本文的主要贡献有2个方面:

1) 使用蒙德里安森林的级联搭建蒙德里安深度森林，级联的每层接收原始特征和前一层输出的变换后特征作为输入.同时进一步提出了一种自适应机制，通过调整原始特征和变换后特征的权重进一步提升性能.蒙德里安深度森林不仅提升了多个数据集上的预测性能，同时也改善了蒙德里安森林无法处理大量无关特征的问题;

2) 首次将深度森林拓展到增量学习的设定中，有效降低了深度森林在每次接收到新样本后的训练时间.蒙德里安深度森林取得了和定期重新训练的gcForest有竞争力的预测准确率，同时训练速度提升了一个数量级.

1 相关工作

1.1 深度森林

深度森林是一种非神经网络的深度模型，其中gcForest[6]是第1个深度森林模型.gcForest有着级联森林结构，级联的每层由多个决策树森林组成，包括随机森林[15]和完全随机森林[16].其中的每个决策树森林输出它估计的类别分布，形成类概率向量.这些类概率向量作为增广特征，和原始输入特征拼接在一起，共同输入下一层.级联每增加新的一层，可通过交叉验证估计整个级联的性能.如果没有达到要求的性能提升，则终止训练过程.因此，深度森林可以自动确定级联层数，即根据数据自动确定模型复杂度.

在实际应用中，已将gcForest在一个工业分布式机器学习平台上实现，并用于某大型企业的现实世界非法套现检测，其性能表现超过了包括深度神经网络在内的其他方法[17].理论方面，文献[18]将深度森林重新形式化为加性模型的形式，并从间隔理论的角度为深度森林提供了一种新的理解方式.此外，文献[19]和文献[20]分别将深度森林拓展至多示例和多标记的学习问题并取得了好的效果.

1.2 蒙德里安森林

在蒙德里安树中，各节点的划分选择不依赖于数据标记，这使其区别于绝大多数的决策树森林.在蒙德里安树的每个节点，根据节点内数据在各维度上的范围随机采样得到划分维度和划分点.同时蒙德里安树的每个节点与一个分裂时间对应.这样的划分机制和分裂时间机制使得蒙德里安树能够高效地更新.当一个新的训练样本出现，根据其与节点内已有数据的相对位置，蒙德里安树可以在3种方式中选择：1) 在当前划分之上引入一个更高层次的划分；2) 更新当前划分的范围使其包含新出现的训练样本；3) 将当前叶节点划分为2个子节点.也就是说，蒙德里安树可以对整棵树的结构进行修改，而其他增量随机森林只能更新叶节点[11-12].对于一个测试样本，一棵蒙德里安树输出各标记上的预测分布.蒙德里安森林是多个独立训练的蒙德里安树的集成，它的输出是其中各棵树的预测值的平均.

此外，蒙德里安森林还被应用于大规模回归任务中[21].文献[22]中得到了关于蒙德里安森林的一致性的理论结果，在随机森林的理论方面有所推进.

2 蒙德里安深度森林

本节我们提出了蒙德里安深度森林，它将增量学习的能力融入了级联森林的结构中.

2.1 级联森林结构

蒙德里安深度森林具有级联森林的结构，级联的每一层含有多个蒙德里安森林，它们的输入是经过前面的级联层处理后的特征信息，并将经过该层处理后的特征信息输出给下一层.

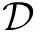
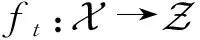
(1)

假设每层只有一个蒙德里安森林，那么第t层ht(·)的输出，也即ft(·)的输出，是一个类概率向量(p1,p2,…,pC).h1的输入是原始特征x，而后每一层ht的输入是原始特征x和前一层输出的变换后特征ft-1(x)拼接成的向量.我们称ft-1(x)为增广特征，如果每层含有多个蒙德里安森林，那么多个类概率向量会被拼接在一起共同作为增广特征.注意到与gcForest不同，这里我们引入自适应因子α来调整原始特征和增广特征的权重.

如图1所示，假设有3个类要预测，那么对于每个样本，每个蒙德里安森林将输出一个3维的类概率向量.假设级联的每一层含有6个蒙德里安森林，那么下一层在接收原始输入特征的同时还将接收3×6=18维增广特征.

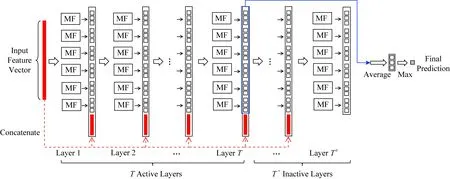
Fig. 1 Illustration of the model structure of Mondrian deep forest图1 蒙德里安深度森林结构

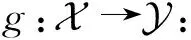
(2)

参考gcForest为了降低过拟合风险所采取的做法，我们使用交叉验证来生成类概率向量[2].与此同时，交叉验证的准确率可以用来估计级联增长至当前层的预测性能.如果新增长的层数没有带来一定的性能提升，那么训练过程将自动终止.这样蒙德里安深度森林自动确定了级联层数T，也即实现了自适应地根据训练数据调整模型复杂度.

在一棵决策树中，每个内部节点j对应于一个划分(δj,ξj)，其中δj∈{1,2,…,D}表示划分维度，ξj表示该维度上的划分点.令Rl(j)和Rr(j)表示2个子节点，一个划分的定义为

(Rl(j)={x|xδj≤ξj},
Rr(j)={x|xδj>ξj}.)

(3)

对于每个节点j，令jd和ujd分别表示节点j中训练数据沿维度d的最小值和最大值，并计算沿各维度d的数据范围rjd=ujd-jd.在蒙德里安树中，以正比于节点内数据在各维度上范围rjd的概率采样得到划分维度δj，即

(4)

其中，Pr表示概率.

换句话说，某维度上的数据范围越大，该维度就越有可能被选为划分维度.通过归一化数据集可使得各维度在初始时有相等的概率被选为划分特征.而后从[jδj,ujδj]中均匀采样得到划分点ξj.可以看出，划分选择是不依赖于样本标记的，当无关特征的比例很大时，每个划分选中有用特征的概率很低，这使得蒙德里安森林无法处理含有大量无关特征的数据集.

在蒙德里安深度森林中，每层接收前一层输出的类概率向量作为增广特征，通过级联结构逐层提升准确率.更进一步，我们在级联结构中引入了自适应机制来平衡原始特征和增广特征的权重，从而防止了增广特征被大量无关原始特征淹没，改善了蒙德里安森林在处理无关特征方面的不足.

我们提出了一种自适应机制，通过自适应因子α，在随机采样划分特征的过程中调整增广特征和原始输入特征的权重.假设增广特征的维数是D′，那么和原始特征拼接后的总维数为D+D′.则选中某个原始输入特征作为划分特征的概率为

(5)

选中某个增广特征的概率为

(6)

自适应因子α是一个可调参数，其设置方式有多种可能性.比如，可以逐层增大或者减小，或者每一层根据不同设置下的交叉验证准确率自适应地决定.本文采用一种简单的平衡策略，即对每个数据集，设置固定的自适应因子α=D/D′，则：

Pr(δj∈{1,2,…,D})=
Pr(δj∈{D+1,D+2,…,D+D′}).

(7)

也就是说，算法在随机采样划分特征时，选中原始特征和选中增广特征的概率相同，可以较为均衡地结合二者的信息.第3节中展示了这样简单的设置方式在不同数据集上有稳定的好的表现.

2.2 批量训练和增量训练

图1展示了蒙德里安深度森林的模型结构.级联森林结构共有T′层，但仅前T层在预测时被激活.这里的T根据2.1节中描述的方式在训练过程中自适应地确定.在批量训练的设定下，T′=T.

在增量训练的设定中，数据随时间分批到达，目标是用新获得的训练数据及时对模型进行更新，使模型充分利用已有的训练数据以期达到尽可能好的预测性能.深度森林gcForest[6]是一个批量学习模型.而对于蒙德里安深度森林，通过逐层更新其中的蒙德里安森林，可以更新整个级联结构.加上动态的对于有效层数的调整，我们得到了一个增量版本的蒙德里安深度森林.它可以从相对简单的模型开始，随着获得更多的训练数据逐步增加模型复杂度以提升性能.

(8)

算法1描述了蒙德里安深度森林的增量训练过程.当接收到第1批训练数据S1时，从零开始训练一个蒙德里安深度森林.设估计的最优层数是T，考虑到随着训练数据的增加可能需要更高的模型复杂度，我们在T层之后训练额外的T+层，它们暂时不参与预测，属于未激活的级联层，则级联的总层数为T′=T+T+，如图1所示.当获得新的训练数据Sk(k>1)时，我们逐层更新蒙德里安森林.在更新过程中，全部T′层都被更新.同时，当前批训练样本的交叉验证准确率随层数的变化趋势可用于决定是否激活更多的级联层用于预测.

在批量训练的设定下，算法1中的第1批训练数据S1即包含了全部训练数据，模型不需要进行更新，将预训练备用层数T+设为0，即得到了蒙德里安深度森林的批量版本.

算法1.蒙德里安深度森林.

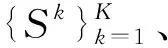
输出：蒙德里安深度森林模型gk.

① 初始化：val0=0,T′=；

② fork∈{1,2,…,K} do

③ 接收新到来的一批样本Sk；

④t=1;

⑤ whilet≤min(Tmax,T′) do

⑧ 计算交叉验证的准确率valt；

⑨ ifk=1∧T′=∧valt≤valt-1then

⑩T=t-1；T′=T+T+; /*用第1批训练数据确定层数*/

3 实 验

我们提出的蒙德里安深度森林(MDF)是一种可以进行增量学习的深度森林，本节我们将MDF与蒙德里安森林(MF)和gcForest进行比较.根据文献[13]，在线随机森林方法ORF-Denil[11]和ORF-Saffari[12]性能接近，而MF和ORF-Saffari相比，训练时间短并且准确率更高，因此我们将MF作为基线方法.而gcForest是一种批量训练的深度森林，它能够在多种任务上达到非常优秀的性能表现[2,6]，我们将使用它的准确率和训练时间作为参考.实验中，我们首先验证了MDF的分类准确率显著优于MF，并且和gcForest很接近，接着展示了MDF增量训练的过程，对不同的方法在增量学习过程中的测试准确率和训练时间进行了比较.

3.1 实验设置和数据集

对所有数据集，MDF使用相同的级联结构，具体来说，每层含有6个蒙德里安森林，每个森林含有20棵蒙德里安树.每个森林输出的类概率向量由3折交叉验证生成，交叉验证的准确率被用于估计级联增长至各层数时的预测性能.如果某层后续3层的性能估计没有提升则训练过程终止，取该层作为输出层.在MDF的增量设定中，我们令T+=3，也就是说，随着训练数据的增加，MDF预测时的激活层数可以自适应地增加至多3层.作为对比的MF采用了120棵树和2 000棵树的配置，后文分别用MF120和MF2000表示.作为对比的gcForest采用和MDF同等的实验配置，即每层由3个随机森林和3个完全随机森林组成，每个森林含有20棵树，级联层数的确定方式也和MDF相同.在增量训练的实验中，考虑到MDF是基于文献[13]的Python版本的MF搭建的，我们自己实现了Python版本的随机森林和完全随机森林，基于它们搭建了gcForest以便于比较训练时间.

MF含有2个超参数.考虑到实验的可比性，我们使用和文献[13]相同的设置.具体来说，一个是生长期限λ，我们令λ=使得该参数不会限制蒙德里安树的深度.另一个是层次规范化稳定过程[23]中的参数γ，令γ=10D，其中D表示特征维数.MDF中作为基本单元的MF和作为对比方法的MF120和MF2000都使用上述的参数设置.此外，MDF还含有额外的参数α，参考2.1节，我们令α=DD′，其中D′表示增广特征的维数.

实验使用和文献[13]相同的数据集，即USPS，SATIMAGE，LETTER和DNA[24].并参照文献[13]的做法，抽取DNA数据集中的第61～120维特征生成DNA60数据集，这是因为MF无法处理大量的无关特征，所以需要选取最相关的60维特征.但我们同时保留了原本的DNA数据集，以展示MDF可以处理含有无关特征的数据集.我们使用和文献[13]相同的训练集测试集划分，具体信息如表1所示:

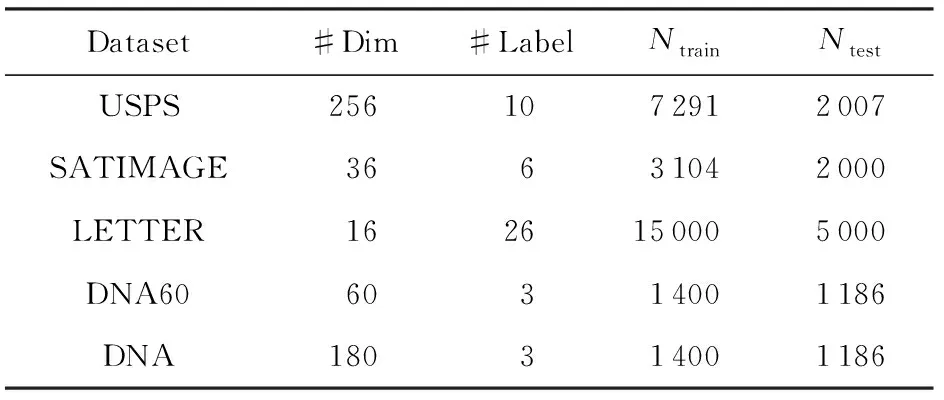
Table 1 Dataset Information表1 数据集信息

3.2 批量设定下的实验结果

我们比较了MDF和MF120,MF2000,gcForest的性能，表2中展示了在每个数据集上进行10次实验得到的测试准确率的均值和标准差，括号中是级联结构的平均层数.注意到MF120等价于我们实验设置下的一层MDF，而MF2000含有比MDF更多的树，即有更高的模型复杂度.表格中用加粗字体标注了每个数据集上平均准确率最高的结果.

比较表2中MF120和MF2000的性能，我们发现增加树的棵数难以提升准确率.而MDF的测试准确率在5个数据集上均显著优于MF120和MF2000，这说明搭建深度模型是有效的提升性能的方式.与此同时，根据MDF在5个数据集上的平均层数，算得分别平均用了792，420，528，456，1 248棵树.也就是说，MDF使用比MF2000更少的树达到了更好的预测性能.如果把蒙德里安树看作基本的结构单元，则实验结果验证了搭建深度模型是比搭建更宽的模型更为有效的提升性能的方式.

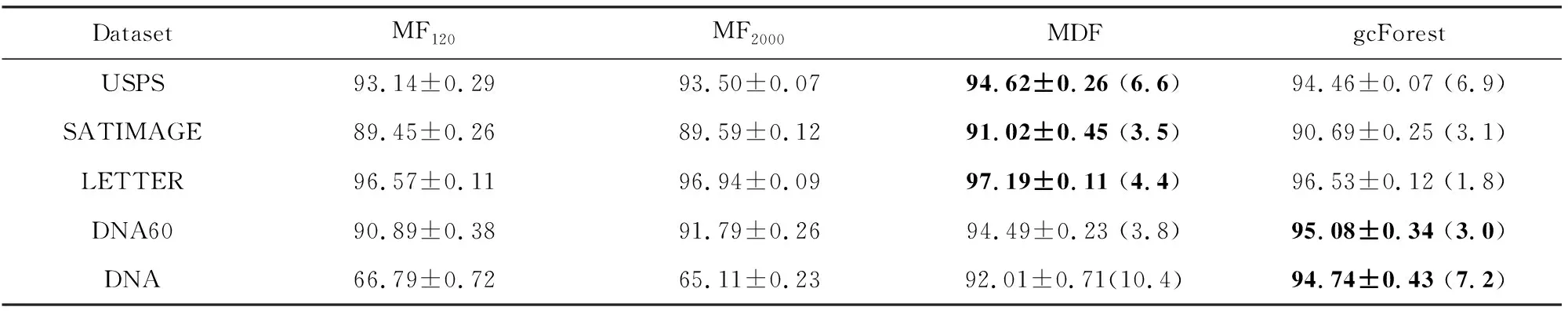
Table 2 Mean Test Accuracy (%) and Standard Deviation表2 批量设定下的测试准确率(%)均值和标准差

MDF训练过程中交叉验证准确率和测试准确率随层数的变化如图2所示.虚线表示训练时交叉验证的准确率随层数的变化情况，横坐标显示至根据交叉验证准确率估计的最优级联层数，可以看到在有效层数内交叉验证准确率逐层上升，不同数据集最终确定的级联层数不同.实线展示了测试集上的准确率，其变化趋势与交叉验证准确率大致相同，因此，根据数据自动确定模型复杂度是有效的.

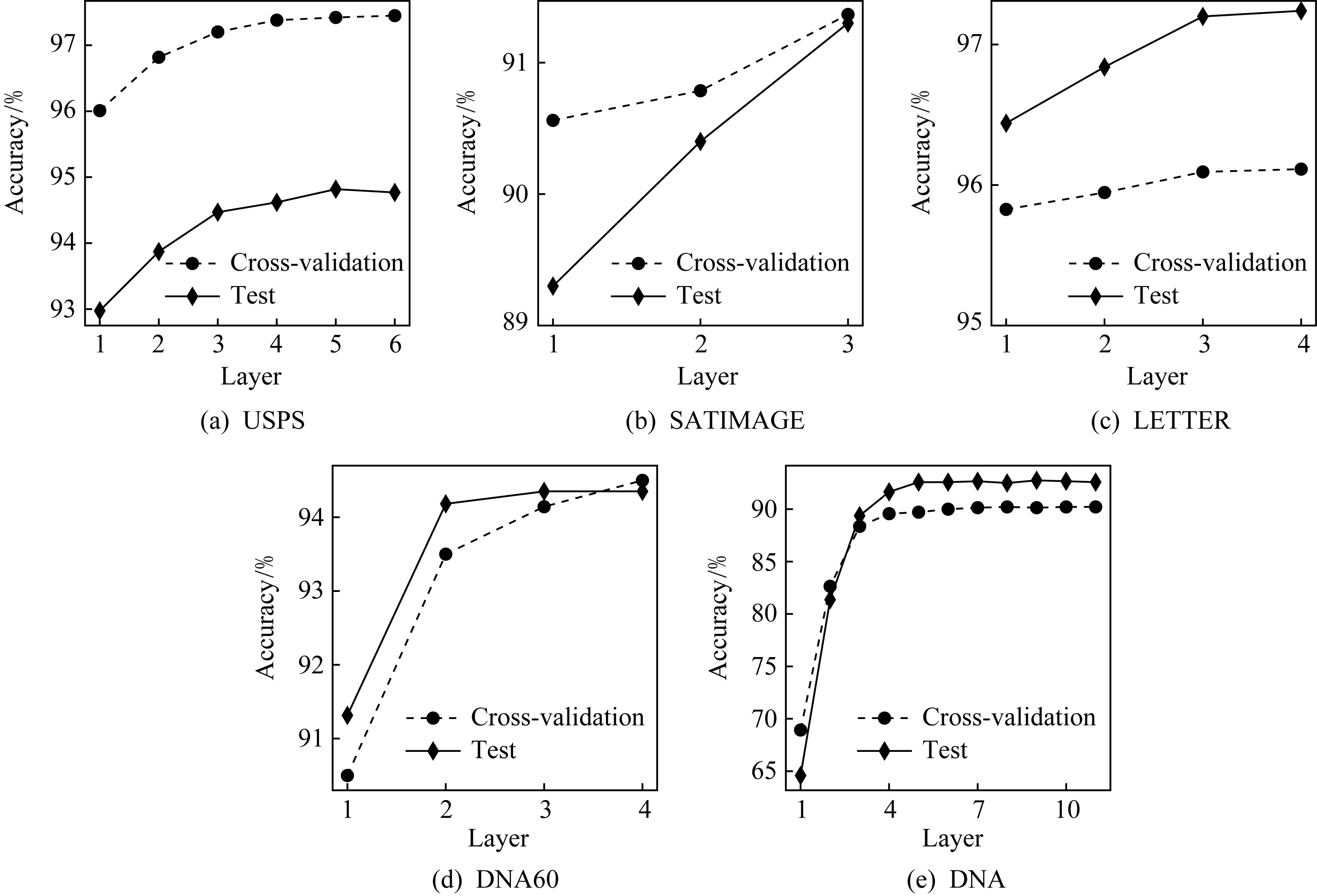
Fig. 2 Cross-validation and test accuracy at each layer of MDF图2 MDF交叉验证和测试准确率随层数的变化

从表2中我们还可以看出，在同等配置下，MDF有着和gcForest接近的预测性能，其中在USPS，SATIMAGE，LETTER这3个数据集上MDF准确率超过了gcForest.文献[6]中指出，易于调参是gcForest相对于深度神经网络的重要优势，gcForest可以使用同样的级联结构在多种任务中达到好的性能表现.而MDF和gcForest同为深度森林，尽管MDF增加了自适应机制，也可以使用固定的设置策略，在不同数据集上都达到好的结果.

3.2.1 自适应因子的影响

表3中将α=DD′的MDF与α=1的MDF进行了10次测试准确率的对比，这里α=1时等价于令MDF的自适应机制不起作用.可以看到，在4个数据集上，设置α=DD′的MDF平均测试准确率高于α=1的MDF.而在DNA60数据集上，尽管不使用自适应机制的MDF平均测试准确率更高，但它们并没有显著的区别.因此，将自适应因子设置为DD′的方式虽然简单，但在实验中是比较有效的.

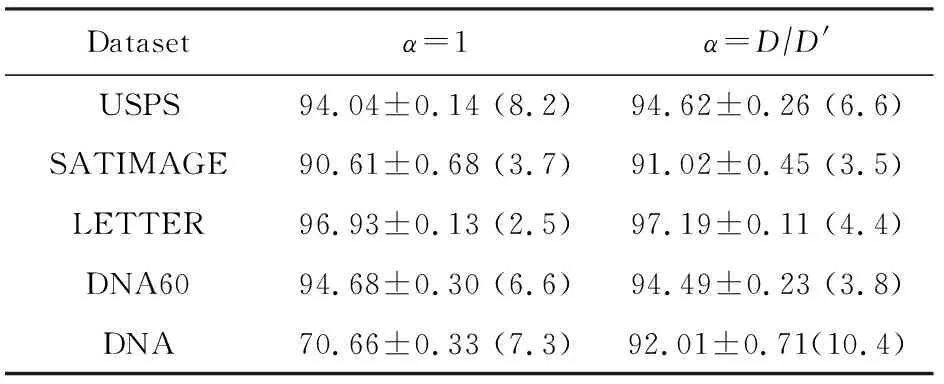
Table 3 Test Accuracy of MDF with Different Adaptive Factors表3 使用不同自适应因子的MDF测试准确率对比 %

图3中以DNA数据集为例，对比了不同自适应因子设置下训练时交叉验证准确率和测试准确率随层数的变化情况，为便于比较，统一了横纵坐标轴的范围.在α=1,α=5和α=20这3种设置中，α=1时算法主要依赖原始特征，无法得到有效的性能提升，一直在较低的准确率徘徊.α=20时算法最为依赖增广特征，可以看到前2层的性能提升非常明显，但很快准确率便停止增长.α=5时算法能够在前5层都维持较为稳定的增长幅度，最终达到较高的准确率.因此，自适应因子α的设置比较关键，过大或过小都不利于最终达到很好的性能.我们注意到，对于实验设定下的DNA数据集，DD′=10，但α=5时的MDF性能最好，其10次平均测试准确率为92.53%.因此，虽然设置α=DD′常常可以得到很好的性能，但最优的α取值和具体的数据有关，若进行调参可能可以达到更好的性能.

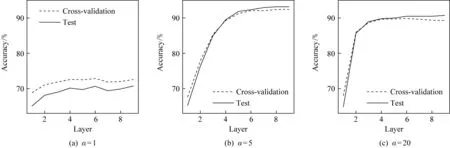
Fig. 3 Cross-validation and test accuracy of MDF on DNA using different adaptive factors图3 在DNA数据集上使用不同自适应因子时MDF交叉验证和测试准确率随层数的变化情况

3.2.2 处理无关特征

文献[13]指出，MF几乎无法处理DNA数据集，因为其含有大量无关特征.而MDF因为其逐层处理和自适应机制，有效地提升了性能.

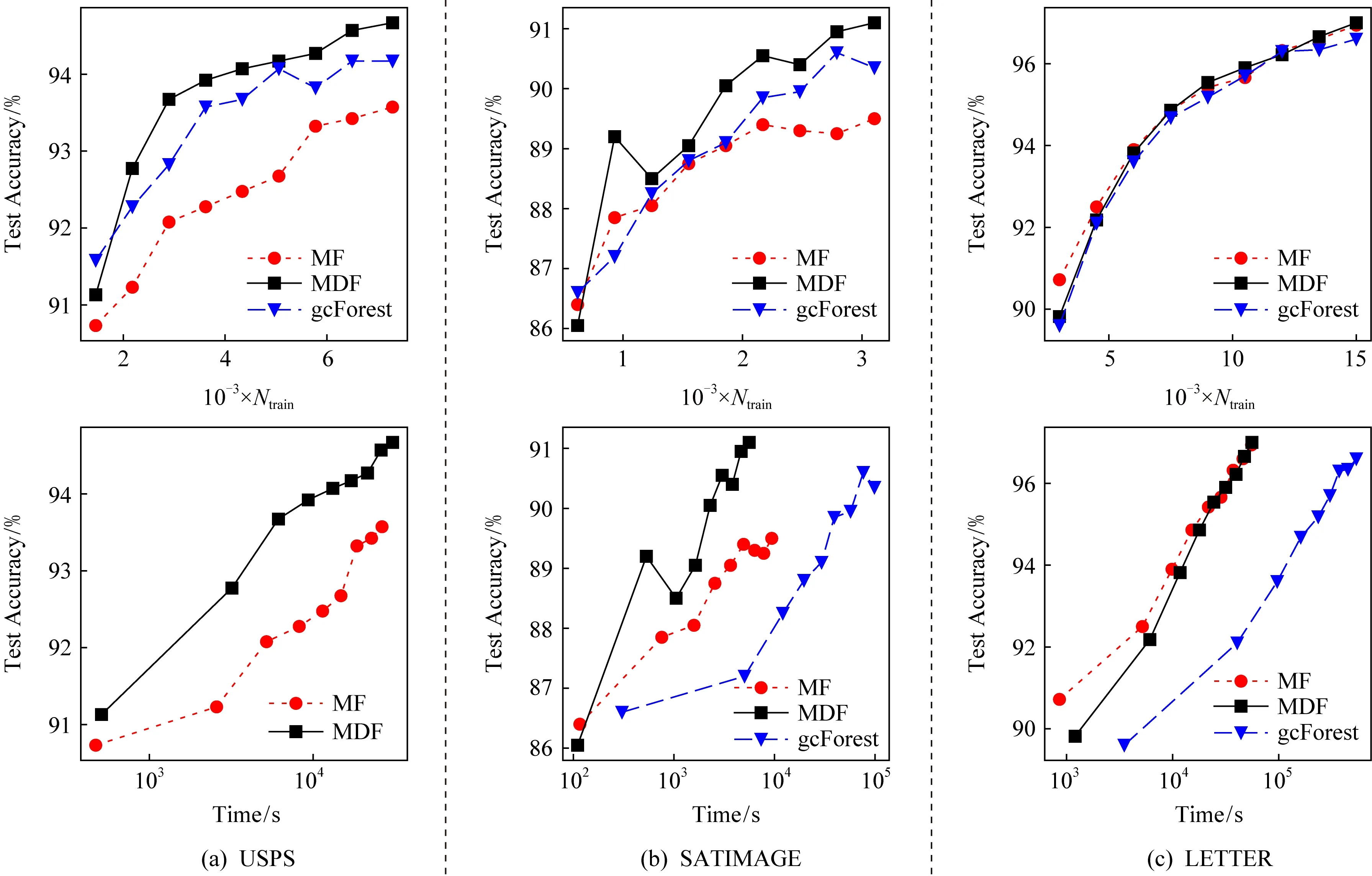
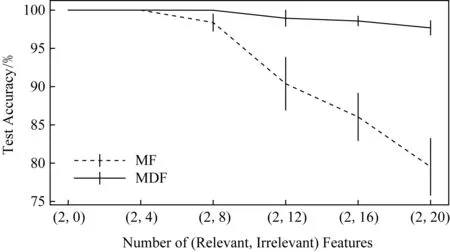
Fig. 4 The influence of increasing irrelevant features on the predictive performance of MF and MDF图4 无关特征的增加对于MF和MDF预测性能的影响

3.3 增量设定下的实验结果

考虑到MF2000中树的棵数超过MDF，我们将MF2000作为基线方法来和MDF比较.同时，为了比较增量训练的MDF和批量训练的gcForest的性能，我们在gcForest的实验中存储当前获得的全部训练数据，每当有新的训练数据到来，把已有的训练数据和新的训练数据合并，重新训练一个gcForest.训练数据被分为81小批，其中第1批包含20%的训练数据，剩余训练数据被等分至后续80批中，每一批训练数据到来时MDF和MF都会进行更新，gcForest进行重新训练，分别记录累计的更新或重新训练的时间.

图5展示了测试准确率的变化情况，每10个小批记录一次.图5(a)～(e)的上层图展示了测试准确率随训练样本数的变化情况，可以看出，在USPS,SATIMAGE,DNA60和DNA数据集上，给定相同的训练样本数，MDF的测试准确率都明显好于MF2000.图5(a)～(e)的下层图展示了测试准确率随训练时间的变化情况.在USPS数据集上，gcForest没有在106s内完成训练，因此未在图中展示.可以看出，在训练时间上MDF与MF2000接近，比定期重新训练的gcForest快一个数量级.值得注意的是，增量训练的MDF有着与定期重新训练的gcForest接近的测试准确率，甚至在USPS,SATIMAGE,LETTER数据集上还略好于gcForest.

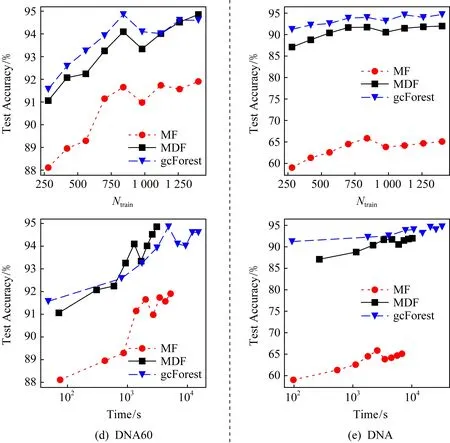
Fig. 5 Results on various datasets in the incremental setting图5 增量设定下在多个数据集上的实验结果

图6对比了自适应增加有效层数与固定有效层数的MDF测试准确率随训练样本数的变化情况.可以看出，在USPS,SATIMAGE,LETTER和DNA60数据集上，激活更多的级联层可以明显提升性能，由此说明了动态调整有效层数的作用.

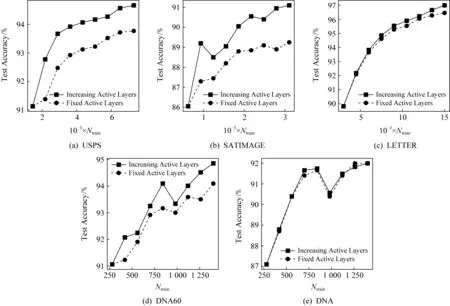
Fig. 6 The effect of adaptively increasing the number of active layers图6 自适应增加有效层数的作用

4 讨 论

深度森林gcForest在级联结构中同时使用了随机森林和完全随机森林2种基本模块以提升多样性，因为在集成学习中，要得到一个好的集成，基学习器应当尽可能准确，同时有尽量高的多样性[25].然而，蒙德里安深度森林仅使用蒙德里安森林作为基学习器，仍然达到了和gcForest接近的准确率.从蒙德里安树的训练过程可以看出，蒙德里安森林有着和完全随机森林接近的随机性，又有着接近随机森林的准确率，这使得蒙德里安森林可以用于搭建同质深度森林.

在批量训练和增量训练下得到的蒙德里安森林的预测精度是相同的[13].而增量训练的蒙德里安深度森林的预测精度要略低于其批量训练版本.这是因为早先到达的训练样本对应的类概率向量已经被用于训练后续的级联层，随着新的训练数据的到达，每一层蒙德里安森林都被更新，但是与先前样本对应的旧的类概率向量已经造成的影响不会被更正.不过，蒙德里安深度森林的性能仍然比蒙德里安森林好许多.

注意到gcForest较高的内存和时间开销约束了大模型的训练，文献[26]提出了置信度筛选的方法，将高置信度的样本直接传递到最后一级，而不是遍历所有层级，同时每层的模型复杂度逐渐增加，由此将gcForest的时间和空间开销降低了一个数量级.蒙德里安深度森林未来也有可能借鉴类似的方法以降低训练的时间和空间开销，从而可以搭建更大规模的模型以进一步提升预测性能.

5 总 结

本文提出了蒙德里安深度森林.它是可以增量学习的深度森林模型，每当获得新的训练数据，它可以基于当前模型进行更新，以提升性能，而不需要重新训练.与此同时，它以蒙德里安森林为基本单元，但能够通过级联森林结构和自适应机制逐层提升预测性能，并且克服了蒙德里安森林易被无关特征干扰的问题，达到了和gcForest接近的准确率.蒙德里安深度森林保持了深度森林超参数少且性能鲁棒的优点，并且模型复杂度可以在训练过程中根据数据自动确定.增量设定下的实验表明，蒙德里安深度森林比定期重新训练的gcForest快一个数量级，并且达到了与之接近的预测准确率.