一种预设转角转速的曲线S实时控制算法

张嘉易，李荣辉，郝永平

(沈阳理工大学 机械工程学院，沈阳 110159)

0 引 言

直驱永磁电机作为机构动力源，具有极大的应用潜力，也成为了近年来研究的热点[1]。直驱电机去掉齿轮减速机构，系统具有惯量小、器件少、功率密度高等优点[2]。直驱电机加速过程通常存在转速和转角位置控制问题[3-4]，不仅要求结构简单实用，更要有具有转速、角位置的实时控制特性[5]。

常用步进电机与伺服电机加减速控制曲线有梯形(线性)、曲线S、指数曲线和正弦曲线等。曲线S加减速一阶连续；正弦曲线可任意次微分。S速度曲线容易数字拟合，计算量小，电机速度的跟随性能好，因此应用最广泛[6-7]。目前，曲线S最大加速度设定为固定值，加速位移大、时间长，一般事先规划好位移加速曲线，不适合直驱永磁电机的快速响应控制。本文阐述一种适合于永磁电机直接驱动控制的实时曲线S加速控制算法。重点研究给定目标转速与转角条件下的实时控制方法，即由电机当前瞬时状态(转速n0，角位置α)实时曲线S加速到目标状态(转速n1，角位置αP)，且时间较短，不失步。

1 算法目标与不失步转矩约束条件

如图1所示，S1，S2两条曲线加速都可以实现速度从n0加速到n1。S1以最大角加速度加速，转角最小为θmin，加速时间TSmin最少。S2为一段加速段和一段减速段曲线构成，其中nQ为S2的最高速度；令加减速度段以相同的较大加速度进行加减速，加减速段时间为T0与T1(总加速时间TS=T0+T1)，加速转角为θ。

图1 曲线S加速示意图

1.1 算法目标

算法目标分为最小转角加速和预设转角、转速情况下加速的控制参数计算。

1) 最小转角加速：计算从当前转速n0加速到目标转速n1的最小转角θmin，最少加速时间TSmin，最大加速度及加加速度等控制参数。

2) 预设转角、转速加速：假定电机当前转速n0，角位置α瞬时加速到目标转速n1，角位置αP。估算以转角θ=αP-α，从当前转速n0加速到目标转速n1的最少加速时间TSmin，最大加速度及加加速度等控制参数。

1.2 不失步的转矩约束

永磁电机加速过程中在不同转速能够输出的最大转矩Mc(n)必须大于等于额定负载转矩Mp(n)与电机加速产生的附加转矩Ma(n)之和，即：Mc(n)-Mp(n)-Ma(n)≥0。

令剩余输出转矩为M(n)=Mc(n)-Mp(n)，则不失步的转矩约束函数F[M(n)]可表示如下：

F[M(n)]=M(n)-Ma(n)≥0

(1)

令ML(n)为线性加速时附加转矩，MS(n)为曲线S加速时附加转矩，则线性加速时Ma(n)=ML(n)，曲线S加速时Ma(n)=MS(n)。

2 曲线S加速控制算法

本文在讨论线性加速与曲线S加速相关参数对应关系的基础上，分析曲线S加速的实时响应参数的估算方法。

2.1 线性与S曲线加速的等效对应关系

如图2所示，同样从n0=0加速到n1可以有两条曲线加速，一条是直线L，一条是曲线S。直线L的角加速度等于斜率KL，曲线S的最大角加速度等于斜率KS。

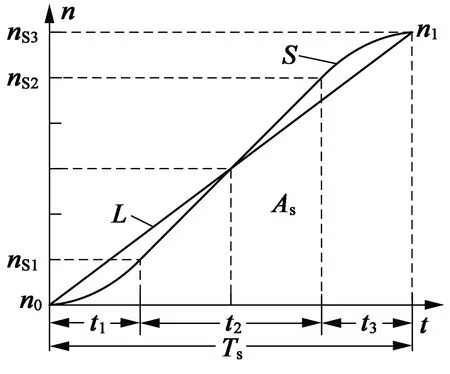
图2 S形与线性曲线加速

t1段:

(2)

t2段:

(3)

t3段:

(4)

KS=4KL/3

(5)

对于复杂的曲线S加速参数计算，可以先通过线性加速方程求得KL参数值，然后由其对应关系转化为曲线S加速参数KS。

2.2 曲线S加速参数计算原理

如图2所示，各时间段的最高转速分别为nS1、nS2、nS3。由式(2)～式(4)的各时间段速度公式可推得当n0≠0时有：(nS1-n0)∶(nS2-n0)∶(nS3-n0)=1∶5∶6，因此可以计算出各段加速后的最高转速nS1=n0+(n1-n0)/6，nS2=n0+5(n1-n0)/6，nS3=n1。

针对图2的曲线加速，其附加转矩曲线如图3所示，其中线性加速时的附加转矩曲线为ML(n)，

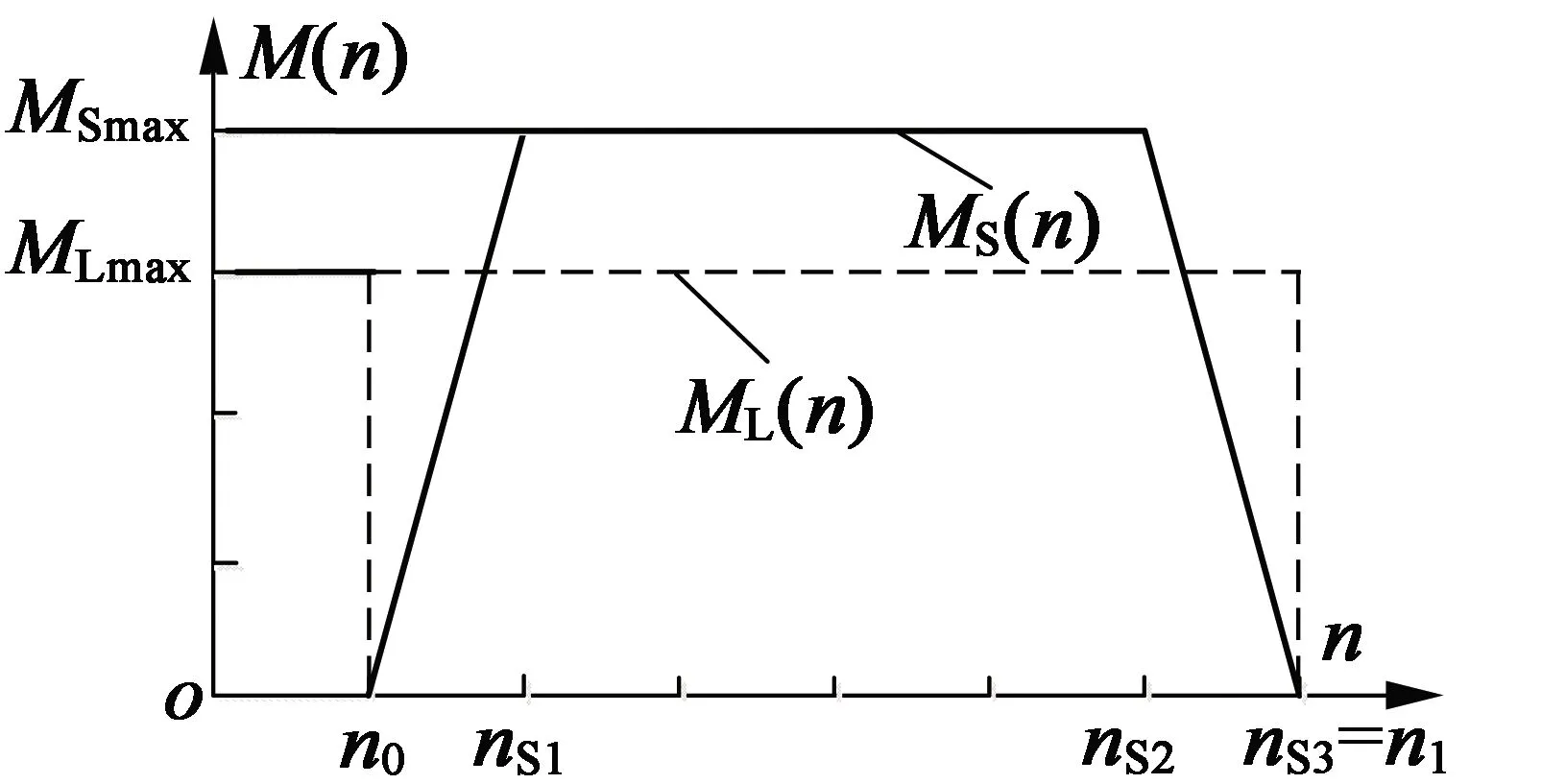
图3 加速附加转矩曲线图

曲线S加速时的附加转矩曲线为MS(n)。ML(n)可表述如下：

ML(n)=MLmaxn0≤n≤n1

(6)

式中：MLmax是定值为线性加速时的附加转矩。由动力学可知，MLmax=2πJKL，其中J为负载机构与电机转子转动惯量的和。由此推得角加速度KL=MLmax/2πJ。再由图2可知，直线L的斜率(即角加速度)KL=(n1-n0)/TS，从而有线性加速总时间计算式TS=2πJ(n1-n0)/MLmax。

参见图3，MS(n)为一分段直线方程可表示如下：

(7)

式中:MSmax为曲线S加速时的最大转矩。由动力学可知：在t2段的最大附加转矩MSmax=2πJKS，得KS=MSmax/(2πJ)。综上是假定MSmax为已知定值的情况下求得的曲线S加速参数，实际上MSmax的大小是由M(n)决定的，因此本文算法最关键的是如何由M(n)函数计算出加速度KS值。为便于计算，将其余参数的计算式表达成已知参数和KS的表达式，如表1所示。

表1 最小转角加速参数表达式

3 最小转角曲线S加速参数KS计算

考虑只有目标转速要求情况下，以最大加速度转过最小转角达到目标转速的S曲线加速参数的计算方法。

如采用线性加速时有Ma(n)=ML(n)=2πJKL，代入式(1)得：

F[M(n)]=M(n)-2πJKL≥0n0≤n≤n1

(8)

式(8)为线性加速时不失步的动力学方程。由式(8)可推导出满足线性加速时的加速度KL≤M(n)/2πJ。由于线性加速时KL值不变，而剩余输出转矩M(n)是随转速n变化的，因此线性加速时的最大加速度KL=min{M(n)/2πJ:n∈(n0,n1)}。

同理，如采用曲线S加速有：

(9)

由式(9)可求出满足曲线S加速的附加转矩最大值MSmax，即分段函数中MSmax最小的上限值，从而可计算KS=MSmax/2πJ。由于M(n)为数值曲线，拟合后形式复杂，难以求取公式解，如图4所示。

图4 Ml(n)拟合曲线原理图

为便于计算，对λ[M(n)]采用分段直线拟合为Ml(n)。为确保Ml(n)≤M(n)，引入参数λ<1，由分段拟合误差确定。Ml(n)函数可表示如下：

(10)

式中：nPi为各直线段端点的转速值，且nP0=0，nPk=nmax为电机最高转速。

将关系式MSmax=2πJKS与Ml(n)代入式(9)，推得曲线S加速时KS上限值如下：

(11)

式(11)为KS的最小上限值不等式函数，其中KS1、KS2及KS3表示曲线S加速各段加速度上限。由此得KS最小上限值：

KS=min{KS1,KS1,KS1}

(12)

为便于计算求解，可将Ml(n)表达成由Pi[nPi，Ml(nPi)]组成的二维数组形式，KS求解过程可简化为在n0到n1的定义域内求一不相交于任何拟合直线段Mi(n)[nPi-1，Pi-1[Ml(nPi-1)]，Pi[nPi，Ml(nPi)]的最大MS(n)梯形区域(见图4)。可利用式(10)中n0到n1定义域内的各直线段方程代入式(11)，再用式(12)求得加速度最小上限值KS，进而求得其他加速参数如表1所示。

4 预设转角转速曲线S参数估算

如图5所示，由于曲线S由加减速段构成，且最高速度nQ未知，无法直接利用式(11)、式(12)求得KS。这时，可先采用数值迭代方法解算nQ的最优解，然后计算加减速段的KS值与其他参数。但由于数值迭代方法计算量过大，不利于实时控制，因此本文根据曲线S与直线L线性加速参数的对应关系式(5)，提出一种快速计算nQ近似值的估算方法。

图5 预设转速与转角曲线S加速

如图5所示，曲线S是由加速段曲线S0和减速段曲线S1构成的。根据曲线S和直线L的对应关系，考虑直线L线性加速时nQ邻域的加速度相同，因此有L0的斜率KL0等于L1的斜率的负值-KL1，即KL=|KL0| = |KL1|；且KL0=(nQ-n0)/T0，-KL1=(nQ-n1)/T1；由此得：

T0=T1(nQ-n0)/(nQ-n1)

(13)

由dα=2πndt，可得已知转角θ计算关系式：

θ=π[(nQ+n0)T0+(nQ+n1)T1]

(14)

由式(13)、式(14)可推得：

(15)

再根据KS与KL的对应关系(KS=4/3KL)，及线性曲线加速力矩Ma(n)=2πJ(nQ-n1)/T1，代入式(1)得：

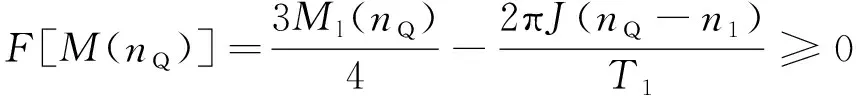
n1≤nQ≤nPk

将Ml(nQ)的分段函数Mi(nQ)=ain+bi与式(15)T1表达式代入上式，整理后得如下条件函数：

(16)

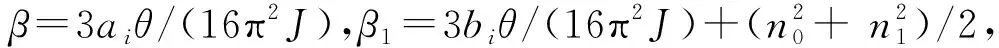
输出：nQ最大值；

Step1：搜索满足直线段端点转速nPi≥n1的直线段Mi(nQ)=ainQ+bi；

Step2：由ai，bi求得β，β1；

Step3：根据式(16)计算F[M′(nPi-1)]与F[M′(nPi)]；

Step4：如果F[M′(nPi-1)]≤0且F[M′(nPi)]≤0，则i=i+1，转到Step2；

(17)

式(17)表示在转速与角位置约束下，加速过程中满足以较大角加速度所能达到的最高转速nQ。将nQ代入式(13)和式(15)求得加速段时间T0，减速段时间T1，求得KL=(nQ-n1)/Tl，求得对应的曲线S加速度KS=(4/3)KL，进而求得全部曲线S加速控制参数,如表2所示。

表2 预设转速、转角加速参数表达式

利用以上计算过程，可以计算出直驱电机从瞬时状态(转速n0，角位置α)到目标状态(转速n1，角位置αP)的曲线S加速控制参数。

5 测试分析

本文编写了曲线S加速参数估算的DSP例程，并以某一直驱同步伺服电机相关参数为例,进行曲线S加速参数实时估算。已知电机负载机构+转子转动惯量J= 1.67 kg·cm2；额定工况下各转速剩余输出转矩M(n)曲线及分段直线拟合曲线Ml(n)如图6所示。

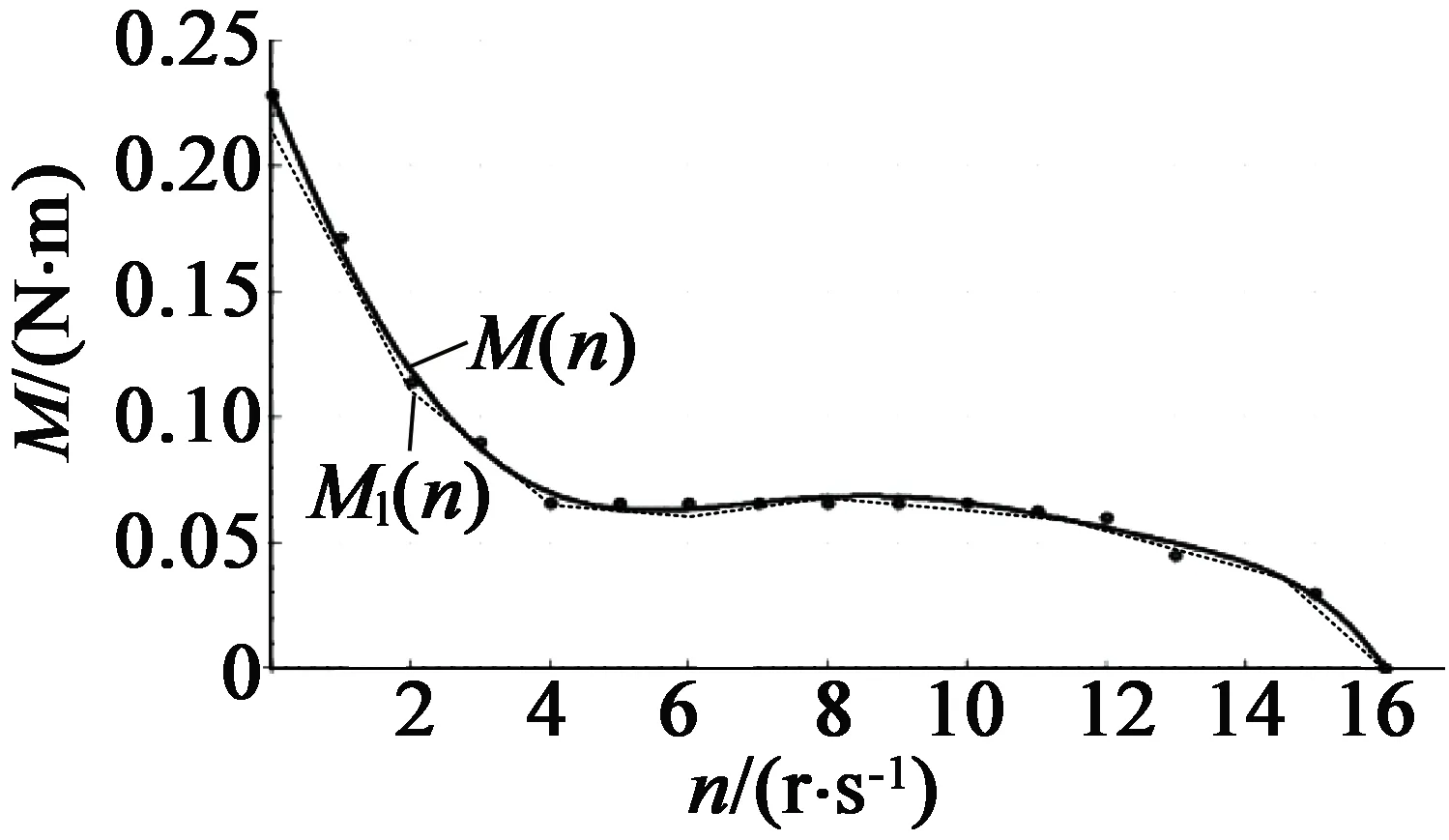
图6 M(n)和Ml(n)曲线

本文曲线S加速参数估算例程的输入参数为电机当前瞬时角位置α、转速n0=0，加速后目标角位置αP(或加速转角θ=αP-α)及加速后目标转速n1。本文为增加测试结果的直观性，设定当前角位置α=0°。应用本文算例估算以转角θ=αP-α，从当前转速n0加速到目标转速n1的曲线S加速控制参数有：加速过程最高转速nQ、最高角加速度KS、加加角速度h、最少加速段时间T0和减速段时间T1。本例程在缺省输入参数αP的情况下，默认计算最小加速转角θmin值并以最小转角加速。

图7为本文方法计算的部分曲线S图。图7(a)为由n0=0经最小转角θmin加速到n1= 5 r/s的曲线S,图7(b)为由n0=0经转角θ=540°加速到n1=5 r/s的曲线S,图7(c)为由n0=5 r/s经转角θ=540°加速到n1= 5 r/s的曲线S,图7(d)为由n0=5 r/s经转角θ=540°减速到n1=0的曲线S。

(a) 95.4°最小转角0～5 r/s曲线

(b) 540°转角0～5 r/s曲线

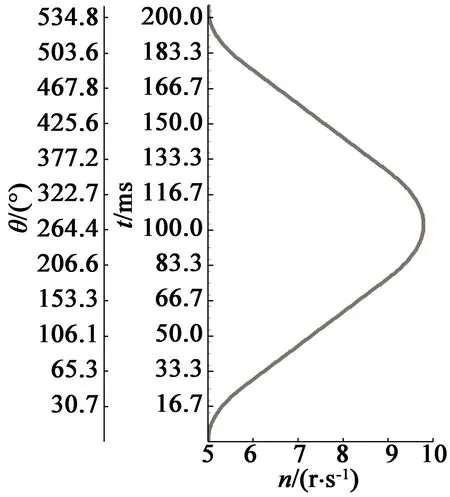
(c) 540°转角5～5 r/s曲线

(d) 540°转角5 r/s～0曲线图7 曲线S算例

表3中列出了各种预设转速转角情况下的计算参数，包括：已知参数θ、n0及n1；计算参数为nQ、KS、h、T0和T1。在采用DSP28335主控芯片、主频150 MHz条件下，利用本文算法编写的实时加速参数计算模块，测试计算过程时间消耗小于25 μs。

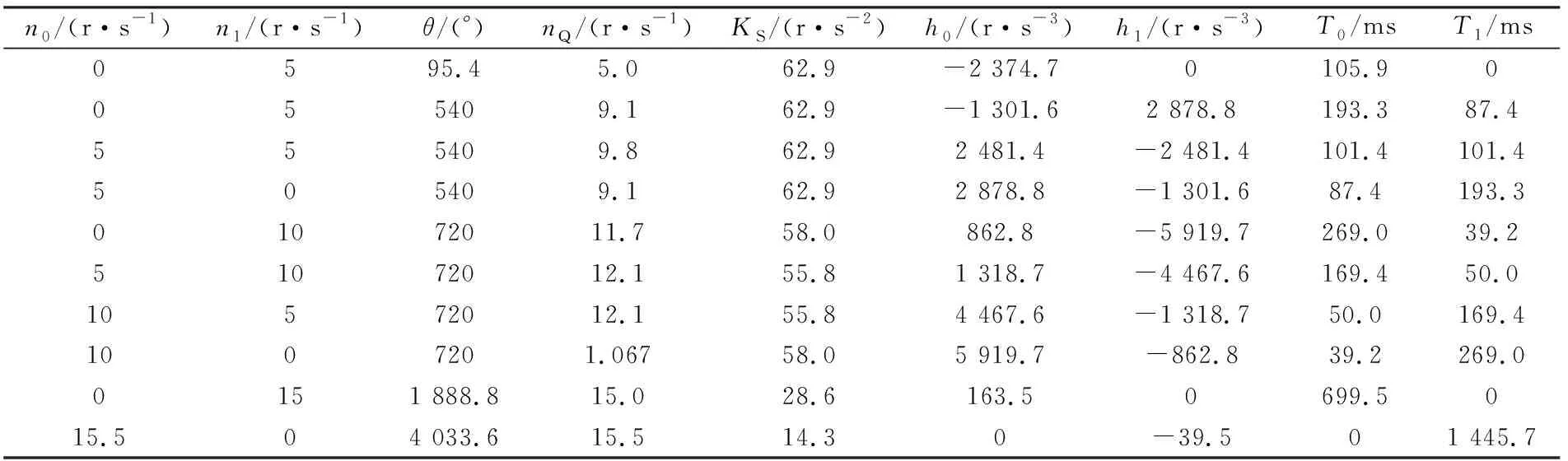
表3 曲线S加速测试数据

以下结果表明，本文算法能够实现直驱电机在预设目标转角和转速条件下的曲线S参数估算，且运算速度在25 μs以内，能够满足电机快速实时响应控制的算法性能要求。

6 结 语

本文重点阐述了一种不失步条件下的转速与角位置实时快速响应曲线S加速控制算法。论述了基于额定负载下剩余输出转矩的最小转角曲线S加速的最大加速度计算方法。阐述了曲线S加速与线性曲线加速的对应关系，推导出一种预设转速与转角条件下的快速响应变速控制参数估算方法。按本文算法编写了例程，并且针对DSP28335控制芯片的实时运算时间消耗小于25μs。该算法测试实例数据表明，应用该方法能够快速估算出预设转速、转角的曲线S加速控制参数，包括最大加速度、加加速度、曲线加速最大速度及最少加速时间参数。该方法对于直驱永磁电机的实时响应加速控制具有借鉴意义。