永磁同步电机伺服系统的变增益自抗扰控制器设计

张 磊，鲁 凯，田 伟，丁 浩

(中国石油大学(华东) 新能源学院，青岛 266580)

0 引 言

永磁同步电机(以下简称PMSM)无需额外励磁电流且能量密度大，特别适用于工业控制领域[1]。PMSM具有参数时变、强耦合、非线性的特点[2]，传统的PID控制器无法满足对负载的突加扰动作出迅速、准确、微超调的动态响应[3]。由韩京清提出的自抗扰控制(以下简称ADRC)方法，使用系统输入输出数据对被控对象的不确定因素进行估计和补偿[4-6]。该技术已在工业机器人、航空航天、电机控制等领域得到了广泛应用[7-10]。ADRC的核心是扩张状态观测器(以下简称ESO)，ESO分为两种形式：非线性ESO和线性ESO,非线性ESO的结构复杂，其严格稳定性很难推导证明。此外，为了获得良好的性能，线性ESO需要更大的观测器增益[11]。基于上述分析，设计一种变增益ADRC。

本文将变增益ADRC应用到PMSM伺服方案设计中，采用变增益ADRC解决传统方法的初始峰值问题，既保留了非线性ADRC的优良特性，又具备线性ADRC的参数调节方便和利于理论分析的优点。在建立PMSM伺服系统数学模型的基础上，结合变增益ADRC设计转速和电流控制器，并进行相应的仿真研究与实验验证。

1 PMSM数学模型

PMSM在d,q旋转坐标系下的电压和磁链方程可以表示：

(1)

(2)

电磁转矩和运动方程：

Te=1.5p[ψf+(Ld-Lq)id]iq

(3)

(4)

式中：ud，uq分别是定子电压的d，q轴分量；id，iq分别是定子电流的d，q轴分量；Rs是定子电阻；ψd，ψq为定子磁链的d，q轴分量；ω是电角度；Ld，Lq分别是d，q轴电感分量；ψf代表永磁体磁链；B为摩擦系数，p为电机极对数。

对于表贴式PMSM，有Ld=Lq，式(3)简化:

Te=1.5pψfiq

(5)

2 基于变增益ADRC的PMSM伺服系统的模型建立

ADRC由跟踪微分器(以下简称TD)，非线性状态误差反馈律(以下简称NLSEF)和ESO组成[4-6]。本节讨论变增益ADRC的设计以及转速环和电流环的变增益ADRC的设计方法。

2.1 变增益ADRC设计

针对一个一阶系统可以写成如下的形式：

(6)

式中：x1，x2为系统状态变量；y为系统输出；u为控制量；f1为系统总扰动；b0为控制增益。建立与该系统对应的ESO:

(7)

式中：e为ESO的观测误差；z1，z2为ESO观测值；l1(t)，l2(t)为ESO的增益。根据式(6)、式(7)得出系统的误差模型如下:

(8)

根据对偶性可以将式(8)转化为标准形式的可控系统，将式(8)写成矩阵的形式如下：

(9)

可以求取误差的解：

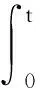
(10)

系统eAt在初始时刻因为高增益很大，且系统的初始误差较大，采用常数高增益观测器会出现初始峰值振动现象。因此，设计了变增益自抗扰控制器。

与式(9)对应的标准系统如下：

(11)

式中：a1(t)，a2(t)为变增益的参数。定义式(9)的可控矩阵为M，式(11)的可控矩阵为Mc。

(12)

式中：p1，p2为M的列向量。根据式(12)可以求出：

(13)

式(9)和式(11)是可控的，定义z=T(t)e，其中变换矩阵T(t)：

T(t)=Mc(t)M-1(t)

(14)

假定a1(t)，a2(t)光滑且有界，通过式(13)、式(14)很容易证出T(t)是一个李雅普诺夫变换矩阵。由李雅普诺夫变换可得：

(15)

为了得到观测器增益l1(t)，定义：

L(t)=[-l1(t),-l2(t)]T

(16)

将T(t)分解为n+1列向量的形式：

T(t)=[T1(t),T2(t)]

(17)

根据式(15)可以得到:

(18)

通过将状态误差矩阵式(9)转化为标准型式(11)，得到了观测器增益表达式:

(19)

对于二阶ESO，可以选取[12]：

(20)

根据式(19)、式(20)可以得到：

(21)

式中：ωn(t)=ω0ω(t)，ω(t)=1.8[(1+e-0.05t)-1-0.5]+0.1。

2.2 转速环变增益ADRC设计

速度控制器的TD主要根据指令安排过渡过程。速度控制器的TD设计：

(22)

式中：ωt为期望速度；ω1的为期望速度安排的过渡过程；ω2为ω1的微分信号；h为步长；参数h0的作用是于消除超调现象；参数r的作用是决定跟踪期望信号的速度。

根据速度环的运动方程,结合提出的变增益ADRC设计方法，选取输入量u=iq,输出量y=ω,状态变量x1=ω和x2=f1=-Tl/J-Bωm/J，设计速度控制器的状态观测器:

(23)

设计速度控制器的控制规律：

(24)

速度控制器如图1所示，其中，z1是ω的观测值，z2是f1的观测值。

图1 速度自抗扰控制器结构图

2.3 电流环变增益ADRC设计

电流环的变增益ADRC设计与速度环的变增益ADRC设计类似。同样地，可以采取一阶ADRC结构设计电流环控制器，不同的是电流环和速度环选取的输入输出量和扩张状态观测器的状态变量不同。将d,q轴电压方程改写：

(25)

电流环选取输入量u=ud，输出量y=iq，状态变量x1=iq，x2=f1=(-Riq+ωeLqiq-ωeψf)。电流环和速度环的结构相同，不同的是二者控制器的参数需要独立调节。电流环控制器结构如图2所示。其中，z1是iq的观测值，z2是fiq的观测值。

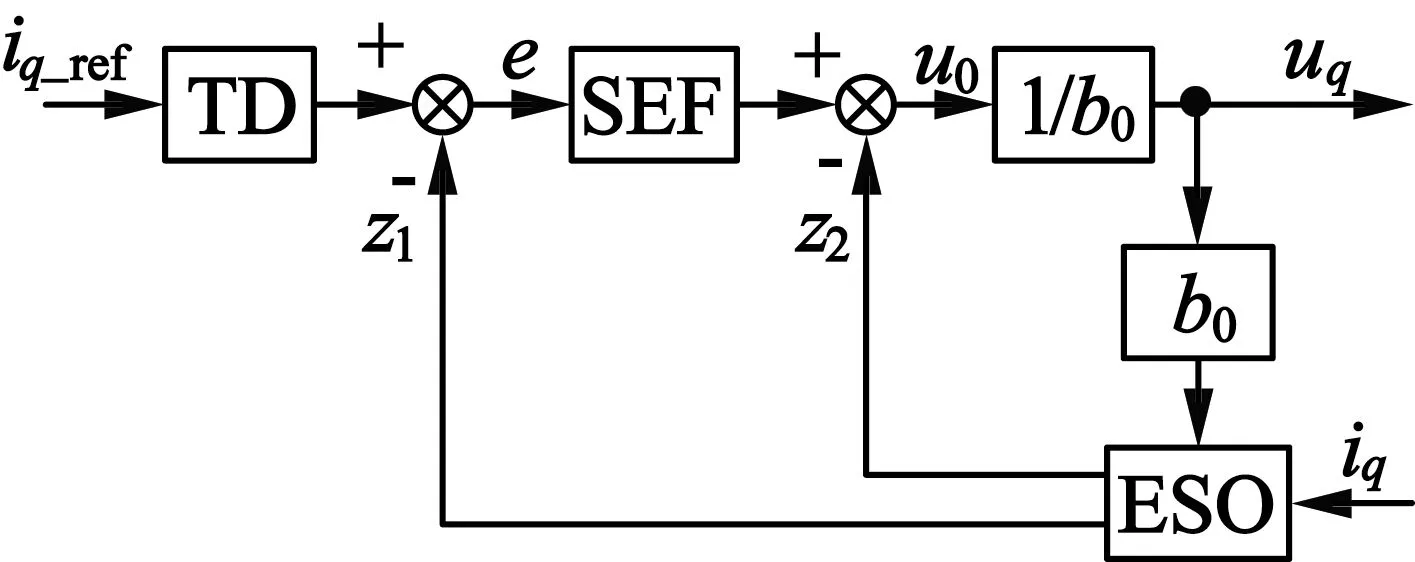
图2 电流自抗扰控制器结构图

3 仿真分析

使用MATLAB/Simulink平台，验证提出的基于变增益ADRC的PMSM控制方案的性能。电机参数如表1所示。其中，速度控制器PI参数：kp=8,ki=2；速度ADRC参数：r=10,h=0.000 3,h0=0.000 5,ωc=40,ω0=80,b0=350。电流控制器PI参数：kp=100,ki=10；电流ADRC参数：r=5,h=0.000 3,h0=0.000 5,ωc=25,ω0=50,b0=200。

表1 电机参数

本文主要进行了起动和抗负载扰动的仿真分析。起动仿真中速度的给定值为150r/min，q轴电流的给定值为1A。在速度环的抗负载扰动仿真中，t=0.4s突加负载转矩5N·m，t=0.8s突加负载转矩10N·m。在电流环的抗负载扰动仿真中，t=0.2s突加负载转矩5N·m，t=0.4s突加负载转矩10N·m。仿真结果如图3和图4所示。

(a) 速度波形

(b) 电流波形图3 起动仿真波形

(a) 速度波形

(b) 电流波形图4 抗负载扰动仿真波形

图3(a)和图3(b)分别为变增益ADRC和传统ADRC速度和电流起动的仿真结果。在图3(a)中，线性ESO为传统ADRC，自适应ESO为变增益ADRC，可以看出，二者都有较好的起动性能。但是，线性ADRC为了追求较好的动态响应，而选取较大的观测器增益，相比变增益ADRC，其速度环和电流环都有起动峰值问题。变增益ADRC就可以解决观测器初始峰值。

图4(a)为ADRC控制器和PI控制器速度抗负载扰动的仿真波形，图4(b)为ADRC控制器和PI控制器电流抗负载扰动的仿真波形。针对同一种负载扰动，速度环和电流环中ADRC控制器的超调相比PI控制器的超调量分别大约降低20%和28%，ADRC控制器没有PI控制器的振荡过程，可以直接恢复稳态；且可以看出，二者的调节时间基本相同，但是ADRC控制器的超调量小于PI控制器，而且负载转矩越大，超调量对比效果越明显。

4 实验结果及误差分析

为了验证提出的基于变增益ADRC的PMSM控制方案的控制效果，搭建如图5所示的实验平台，PMSM具体参数如表1所示。

图5 实验装置图

对速度环进行起动和抗负载扰动实验，起动实验结果如图6所示；抗负载扰动实验结果如图7所示。其中，给定转速为150r/min，系统稳定时突加5N·m负载转矩。

图6(a)为线性ADRC的速度曲线，图6(b)为变增益ADRC的速度曲线，可以看出采用变增益ADRC可以较好地解决传统ADRC的初始峰值现象。图7(a)为PID控制器的速度曲线，图7(b)为ADRC的速度曲线，可以看出，采用变增益ADRC有着较好的动态性能。

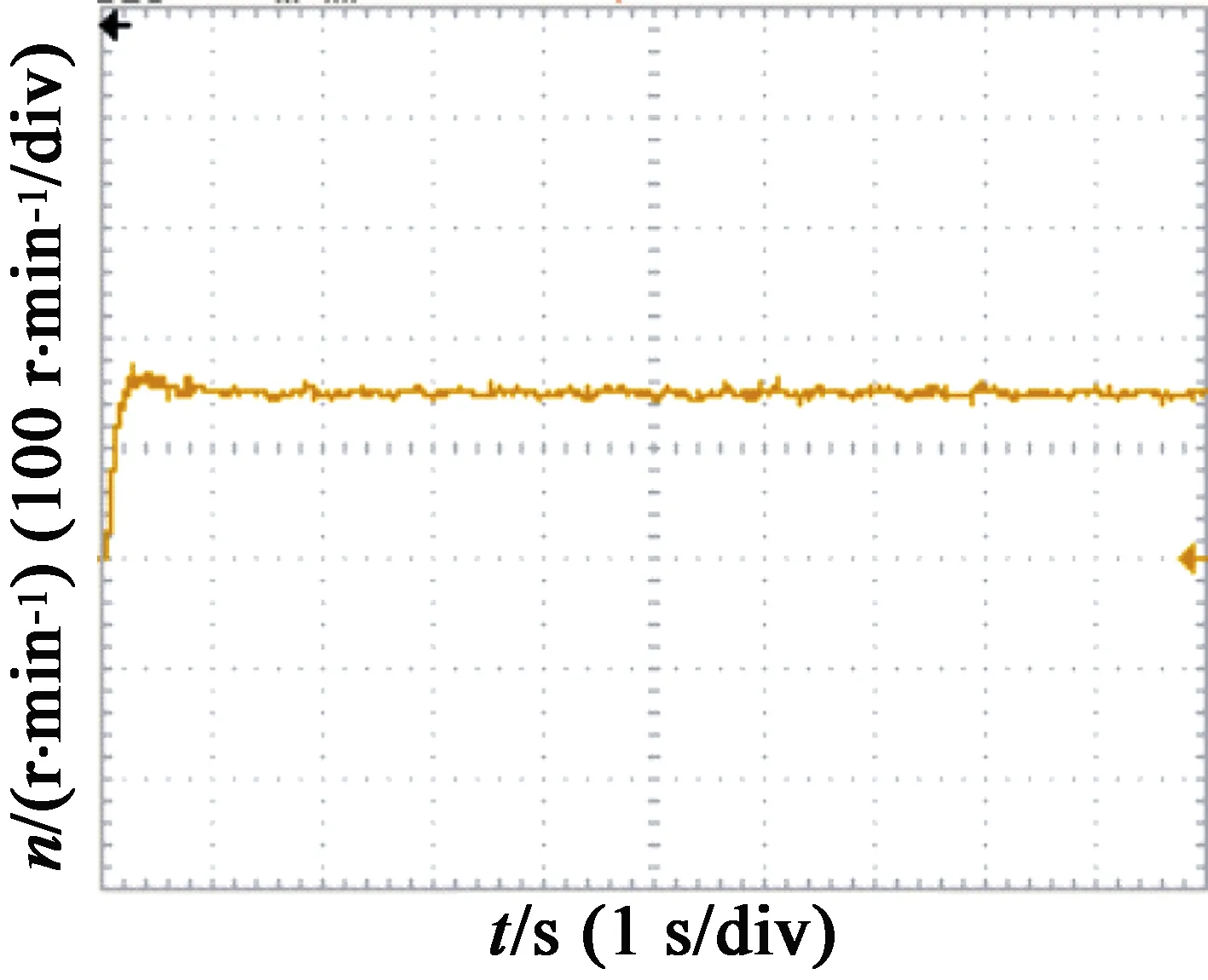
(a) 线性ADRC速度曲线

(b) 变增益ADRC速度曲线图6 起动实验波形

(a) PID速度曲线

(b) 变增益ADRC速度曲线图7 抗负载扰动实验波形

5 结 语

本文分析了线性ADRC应用到PMSM中存在的初始峰值现象，提出一种基于变增益ADRC的PMSM转速和电流控制器，采用变增益ADRC可以解决传统方法存在的初始峰值问题，既保留了非线性ADRC的优良特性，又具备线性ADRC的参数调节方便和利于理论分析的优点。与传统的PID控制相比，在应对突加的系统扰动方面，变增益ADRC伺服系统的收敛速度更快，静态误差更小，系统的性能得到较大程度的提升。由仿真和实验结果可知，起动和动态时的系统运行都符合理论分析。