基于SPA-SVDD方法对间歇过程的故障检测
2020-08-24谢彦红薛志强
谢彦红, 薛志强, 李 元
(沈阳化工大学 技术过程故障诊断与安全性研究中心, 辽宁 沈阳 110142)
间歇过程是工业中比较常见的一种生产过程.相比于其他的工业生产过程,间歇过程具有高效、灵活、柔性生产等特点,但产品质量易受原材料、设备状况、环境条件等不确定性因素的影响.为了保障间歇生产过程的安全平稳,同时提高产品质量和生产效率,针对间歇过程的故障检测和诊断方法日益受到重视[1].
基于数据驱动的统计过程监控从历史生产数据出发,通过对过程测量数据的统计建模和分析,判断过程所处的运行状态,在线检测和识别过程中出现的异常工况,实现过程的安全、稳定运行,最终达到提高产品质量和提升企业经济效益的目的.传统多向主元分析(multi-way principal component analysis,MPCA)方法[2-3]是一种典型的基于数据驱动技术的过程故障检测方法,针对间歇过程具有非线性、非高斯分布、多阶段性等复杂的数据特性,MPCA作为传统的线性检测方法并不能有效地进行故障检测.此外,应用MPCA模型过程监测时,需要所有间歇数据等长,在线监测时需要调整数据结构,这些问题都会影响过程监测结果的准确性.
针对间歇过程数据的非线性和不等长特征,He[4-5]等、李元[6-8]等提出一种基于统计模量故障检测方法,并将其应用在间歇和连续生产过程中.在统计模量框架下依托K近邻(Knearest neighbor,KNN)方法[9-14]进行检测,繁重的数据计算严重影响检测的效率.间歇过程数据具有多模态的特性,各模态数据结构离散程度差异较大时,检测效果也会不理想.Xu[15]提出了一种基于统计局部性保留投影(SLPP)的局部和非高斯特征提取方法.首先,利用统计模式分析(SPA)构造过程统计量,利用高阶统计量掌握非高斯统计量的性质.然后,利用局部保持投影(LPP)方法发现统计量的局部流形结构.利用SLPP模型的T2 和SPE来检测过程故障.Zhang[16]提出了一种局部和全局统计模式分析(LGSPA)方法,该方法将SPA框架和局部投影集成到主成分分析中,利用各种统计信息,同时保留观测数据的局部和全局信息实现故障检测.但该方法并没有解决间歇过程数据的多模态问题.
20世纪90年代末,Tax[17-18]等提出支持向量数据描述(support vector data description,SVDD) 方法,该方法通过映射将低维空间数据投影到高维特征空间并建立模型.SVDD方法可以检测非线性、多模态数据,因此其广泛应用于工业生产过程.谢彦红[19]等针对间歇过程数据存在动态变化特征,传统的支持向量数据描述方法很难实现实时在线状态监测的问题,提出一种基于滑动窗口的SVDD在线实时故障监测方法.李冠男等[20]将SVDD方法应用在冷水机组传感器故障检测中,结果表明SVDD对冷水机组传感器故障检测效果明显,但对于不同传感器的不同幅值偏差故障,故障识别程度并不一致.谢彦红等[21]提出一种PCA-SVDD的故障检测方法.利用PCA方法进行数据维数约减,降低建模过程的计算量,缩减建模时间.
综上所述,针对间歇过程提出一种SPA-SVDD故障诊断方法.通过统计模量分析方法对间歇过程数据进行处理,得到二维的过程统计模量数据;建立SVDD模型,计算模型的超球半径R,将其作为新样本是否偏离正常样本的指标.
1 基于统计模量分析
1.1 多向展开分析
间歇过程采集的数据以三维矩阵形式储存,如图1所示,由于每一批次数据都是矩阵,在检测之前需要预处理为向量形式,通常预处理方法为多向方法.把第i个批次的数据记为
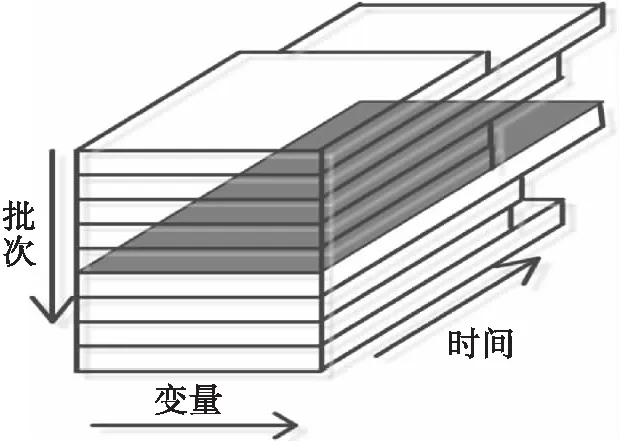
图1 三维数据结构
(1)
多向方法将数据按时间方向展开为
Xi={x11,x12,…,x1j;x21,x22,…,x2j;…;xi1,xi2,…,xij}.
Xi表示第i批次按时间方向展开的向量.使用多向展开方法后数据大小会变成(I×JK).随着时间增加样本数也会增加,为后续建模检测增加负担.除此之外各批次采样数据不等长时需要进行数据截取,以获得等长数据,此方法会导致部分数据信息缺失,影响模型检测的有效性.因此,提出一种新的数据展开方法.
1.2 统计模量分析
统计模量分析是一种数据处理方法,可克服传统多向展开方法在间歇过程中的缺点.统计模量方法就是利用变量的数据特征代替变量数据,常用到均值μij、方差σij、偏度γij、峭度κij等.
(2)
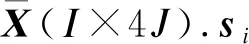
2 支持向量数据域描述
2.1 SVDD原理介绍
SVDD方法目标是构建一个超球面来描述数据的边界.构建的超球需要满足其体积最小,同时保证包含全部(大多数)数据.构建超球的目标函数为
F(R,a)=R2.
(3)
其中:R表示超球面的半径;a表示球心.
当数据中出现偏离的数据时,会导致构建的超球面不能有效地描述数据边界,此时构建的目标函数需要引入松弛向量ξi来调节离散数据对超球面的影响.
(4)
C是惩罚系数,其权衡超球包含数据个数和超球体积的比率关系,通常利用公式
(5)
计算得到.d与置信度相对应,选取99 %置信度则d=0.01.
为保证超球体体积最小,建立约束条件:
(xi-a)T(xi-a)≤R2+ξi.
(6)
从而转化为求解最优化问题:
(7)
利用拉格朗日乘子法求解最优化问题:
(8)
求解(8)得到
(9)
由公式(9)可知:球心是所有数据点的线性组合;数据xi都会被分配系数αi,其中非零系数αi对应的数据xα被称为支持向量,超球体的大小、轮廓正是由支持向量决定的.将式(9)带入式(8),拉格朗日函数问题转化为
(10)
通常原始空间数据不会呈现球状分布,无法利用一个准确的球面边界来描述数据.因此考虑通过映射将数据投影到高维空间,使高维空间数据呈球型分布.通过构建包含高维空间数据的超球面进行数据描述.引入核函数代替高维数据间的内积运算.由于Gaussian核具有更加稳定的数据描述能力,因此通常选取高斯核函数[22-24]作为映射对应的函数:
KG(xi,xj)=exp[-(xi-xj)2/s2].
(11)
其中s为核参数.将式(11)带入式(10)得到

(12)
通过式(12)计算支持向量xα到球心a的距离Rα.
(13)
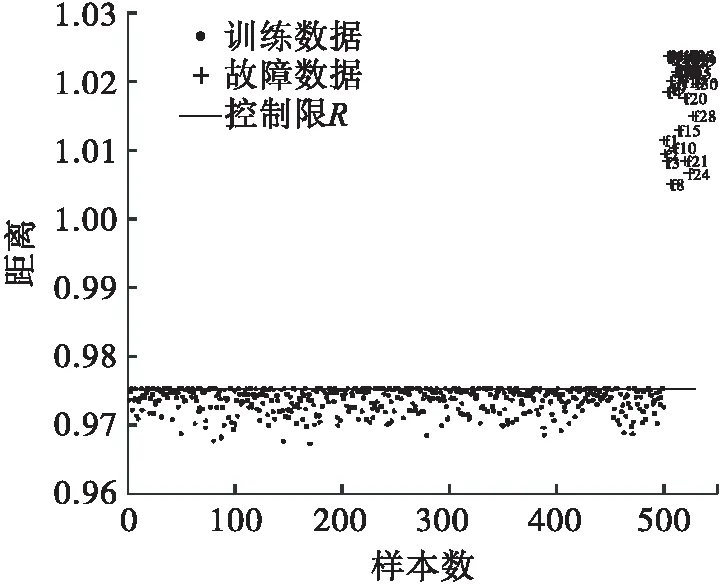
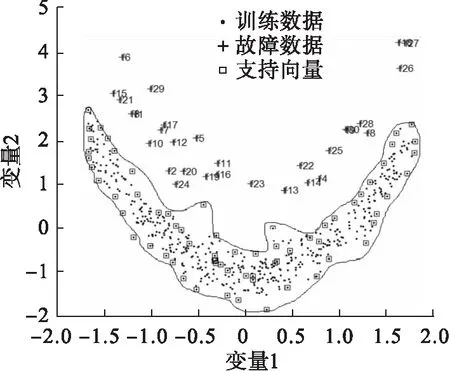
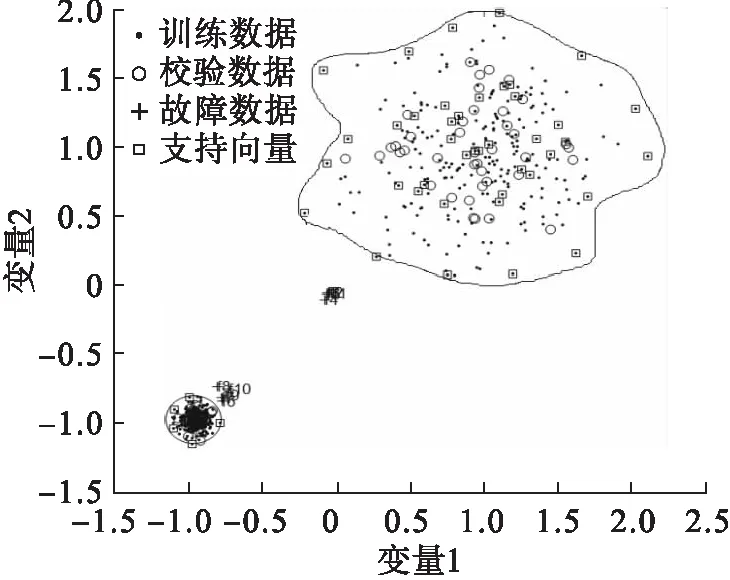
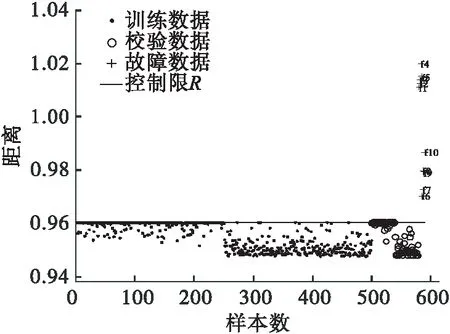
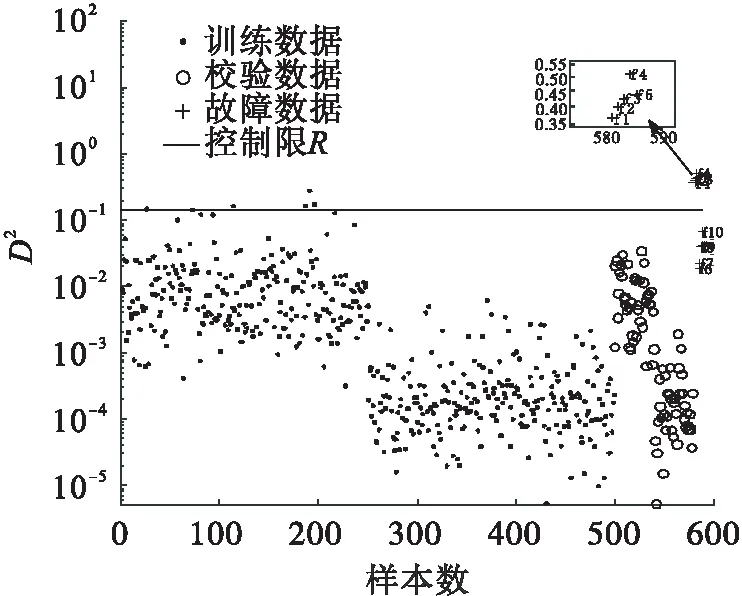
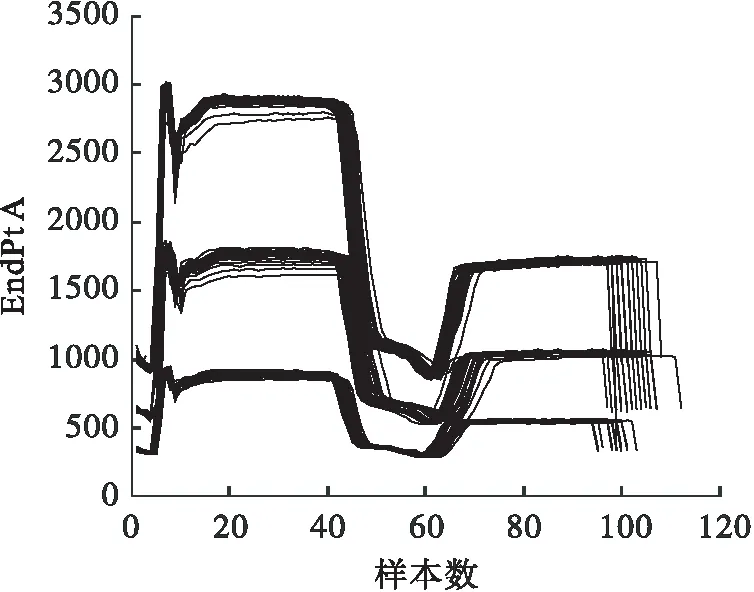
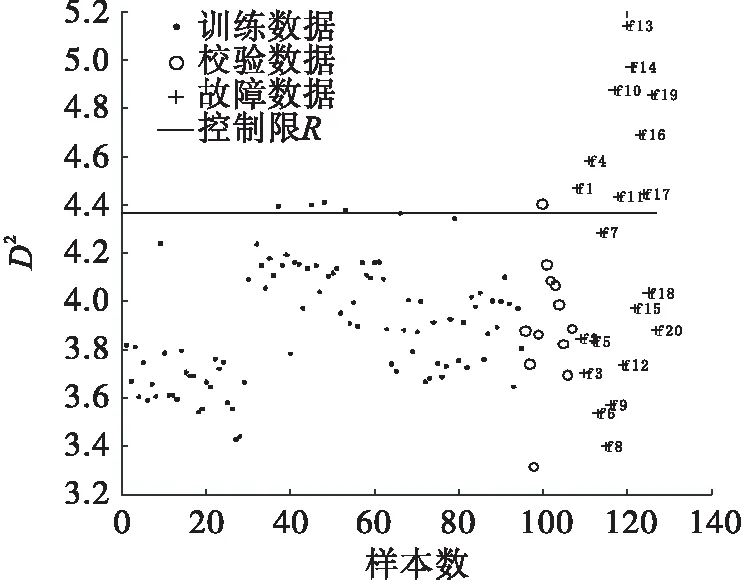
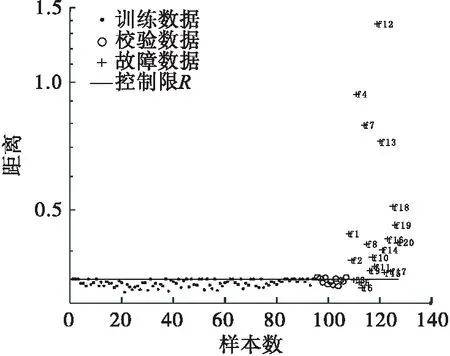
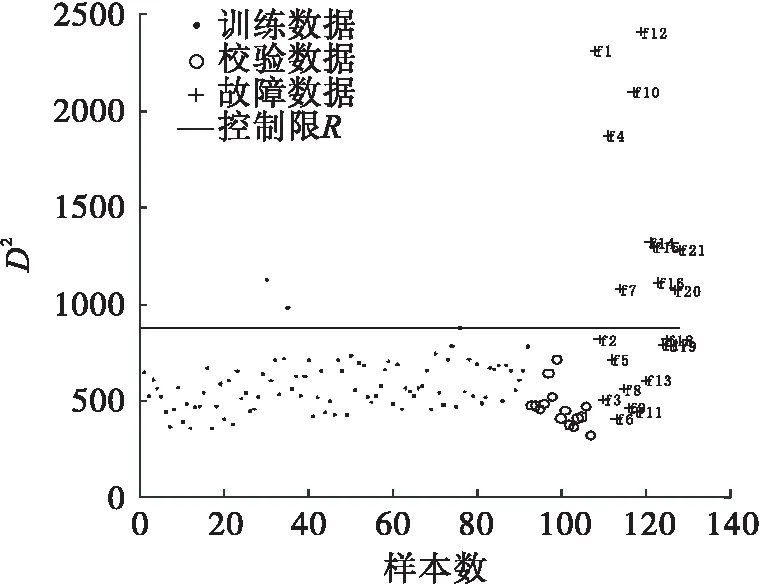
将Rα设定为控制限,当新的样本到球心的距离D 针对非线性数据和多模态数据进行2次实验.通过式(14)得到500个数据作为训练数据X,并通过加入0.65的阶跃信号产生30个故障数据F. (14) e为高斯随机噪声.数据满足非线性特征. 用SVDD对训练数据X进行建模,其中主要参数C可由式(5)确定为0.2,s通过交叉验证法确定为0.4.得到控制限Rα.检测结果如图2所示. 图2 非线性数据SVDD检测图 从图3 可以看出数据的非线性结构,支持向量分布在数据边界上.连接支持向量的曲线为等高线,代表等高线上的数据在高维空间中到球心的距离等于支持向量到球心的距离. 图3 非线性数据轮廓 通过式(15)得到稀疏差异较大的两个模态数据X1和X2,每个模态拥有250个训练样本,40个校验样本.同时生成5个位于模态间的5个故障数据F1和靠近密集模态的故障数据F2. (15) 用SVDD 对训练数据X1和X2进行建模,其中主要参数C可由式(5)确定为0.2,s通过交叉验证法确定为0.6.得到控制限Rα. 图3和图4展示了SVDD描述的训练数据边界(轮廓). 此边界上的点在高维空间中与支持向量到球心距离等高.SVDD方法对边界数据有着严格的界定,当新来数据到球心的距离大于半径时,就会被认定为故障数据.图5和图6分别为多模态数据SVDD检测图和多模态数据KNN检测图. 图4 多模态数据轮廓 图5 SVDD多模态数据检测图 图6 多模态数据KNN检测图 针对多模态数据中各模态稀疏差异较大时SVDD的检测不会受到影响,而KNN方法则会发生检测错误.因为密集模态数据样本近邻之间距离尺度远小于稀疏模态中样本近邻距离.这就会导致靠近密集模态的故障样本计算统计量D2时,距离会被稀疏模态距离尺度覆盖,导致此类故障无法被检测. SVDD方法对于线性、非线性、多模态数据均可以有效地进行数据边界描述,并且对异常值进行准确判定. 半导体数据来源于美国德州仪器公司的半导体生产过程实际数据.半导体工艺过程[25-27]是典型的间歇过程,数据类型是典型的三维数据结构,数据集由3个不同实验共129个生产批次组成,每一生产批次对应不等长的采样时间和相同的21个变量.由于数据缺失,第2个实验的第22正常批次数据(整体数据的第56批次数据)只有3个采样时刻.本文针对数据包里的107个批次和21个故障批次进行数据预处理. 图7为变量EndPt A的变量轨迹,可以看出半导体数据为3个模态数据. 图7 变量EndPt A轨迹 图8 多向展开半导体KNN检测图 图9 多向展开半导体数据SVDD检测图 多向展开方法会增加数据维数从而增加SVDD、KNN计算量和建模时间,同时由于数据采样不等长,需要对数据进行截取,此操作会将有用信息抛弃并且增加多余的信息,从而影响检测结果. 图10 SPA-KNN半导体检测图 图11 SPA-SVDD半导体检测图 文章提出一种SPA-SVDD的故障检测方法,并应用于半导体过程监控和故障检测.实验结果验证了该方法对间歇过程故障检测的优越性,在实际生产中具有较强的指导意义.统计模量分析方法可有效将间歇过程数据的三维数据结构转化成二维数据结构,避免采样不等长带来的问题,同时保留了原始数据特征.SVDD方法对非线性数据、多模态数据可以准确地检测故障.下一步工作方向将会针对SVDD方法中参数的确定、故障的定位及分类.2.2 数值实验
3 仿真实验
3.1 半导体工艺过程介绍及数据处理
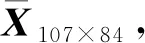
3.2 实例仿真

4 结 论
