环境规制、本地市场效应与产业空间多重均衡
2020-08-22王沛霖庞临然
乔 彬,王沛霖,雷 春,庞临然
(1.太原科技大学 经济与管理学院, 山西 太原 030024;2.澳大利亚纽卡斯尔大学,澳大利亚 纽卡斯尔 2300)
一、引言
产业集聚在带来正向溢出效应的同时,也带来了环境污染等负向效应。环境规制优于其他政策的关键点在于其不是通过中央—地方—企业的强制性被动传导机制,而是通过对企业的生产和管理施加新的约束条件,使得企业必须调整行为(孙学敏,王杰,2014)[1]。但由于区域、产业、企业异质性的存在,以及应对环境规制的能力及策略的差异,必然导致区域、产业及企业竞争力变化,从而改变经济要素空间作用力的均衡机制,引发生产要素的空间流动,进而影响产业空间分布。
二、文献综述
学界对于环境规制的研究多见于对企业(产业)生产率及创新补偿效应的分析(Gray,et al.;Porter,et al.;王兵等,2010;李树等,2013)[2-5];还有一类研究重点从环境与贸易的视角出发,主要关注环境规制对企业出口的影响或是否存在环境避难所等效应的研究(Tobey,1990;Craciela,1995;Busse,2004;傅京燕等,2010)[6-9];也有一些学者对环境规制与产业集聚的关系进行了实证检验(徐敏燕、左和平,2013;闫逢柱、苏李、乔娟,2011;刘习平、宋德勇,2013)[10-12]。学者对于环境规制的研究多集中在对企业(产业)竞争力或产业集聚的理论探究与经验研究,并以新古典经济或者新增长基本理论为框架,尽管在此框架下可以实现生产要素最优配置的一般均衡,却遗漏了空间因素。Krugman[13]开创的新经济地理学把主流经济学长期忽视的空间要素重新纳入到一般均衡分析框架,通过空间作用力分析经济活动的空间分布。此外,近年来“新”新经济地理学(以下简称为NNEG)将企业异质性纳入新经济地理学框架,由于该理论更趋近于现实而得到学界的广泛认同,这为研究环境规制对于产业空间分布影响提供了较好的基础研究框架。
本文将环境规制融入“新”新经济地理学(NNEG)框架,深入研究环境规制对市场效应的影响,理解产业空间分布的变化规律,为推进差别化的区域环境规制由管制向治理转型以及促进区域协调发展提供参考。
三、短期均衡及市场效应分析
(一)环境规制下的短期均衡分析
通过参考新经济地理学FE模型,设定本文的基本假设。假定一个经济系统由南(不发达地区)北地区(发达地区)构成,两个地区的偏好、技术、交易水平、禀赋相同;地区中只存在农业生产部门(A)和工业生产部门(M),其中农业部门生产同质化的农产品,工业部门生产差异化的工业品;企业在生产过程中需要投入两种生产要素即人力资本(企业家H)和一般劳动力(工人L),其中假定人力资本可跨区域流动,一般劳动力只可以在同一区域流动,用*来区分南部地区的变量。
每个地区的消费者都有两个层面的效用函数:使用柯布-道格拉斯型效用函数来表示的总效用函数;使用不变替代弹性(CES)函数来表示的子效用函数。具体如下:
(1)
(2)
其中,工业品种类用i来表示,C代表工业品消费数量,*代表产地在南部地区,μ是消费者的工业品支出比例,1-μ是消费者的农产品支出比例;σ为工业品替代弹性,这里假设为常数。
如果用Y来表示总收入,pi表示消费者消费一单位第i类工业品所需要支付的价格,消费者的消费预算约束为:
(3)
间接效用函数如下:
(4)
其中wH表示企业家的名义收入,wL表示工人的名义收入,P表示消费者生活成本指数,PM表示工业品价格指数。
产业集聚可以使得当地的环境产生污染,区域政府为了约束企业的污染行为从而进行环境规制(宋马林、王舒鸿,2013)[14]。由于在现实中环境规制一般采取征税方式,因此本文使用t和t*来区分两地环境规制行为,这里假定税率不发生变化,用外生常数t(南部为t*)表示。假设企业人力资本为固定投入(即F=1),劳动力和污染成本为可变投入,企业成本函数为:
TC=wH+(wLaM+tγ)x
(5)
其中当产出为x时,需要投入aMx单位的劳动力;当产出工业品x=1时,会造成γ单位的污染。
在该模型中,农业部门为完全竞争的市场结构,不存在环境污染行为,生产者按边际成本定价,因此:
(6)
由消费者预算约束可以得到消费者对农工产品组合的需求函数为:
CM=μY/PM,CA=(1-μ)Y/pA
(7)
通过将式(1)改写成CMPM=μY,假设在没有储蓄条件下,收入水平为Y,支出水平为E,其中,E=wHH+wLL,收入和支出相等,得到消费者对工业产品的支出为μE。在消费者对工业品的支出的约束下,考虑消费者在面对差异化工业品时的效用最大化一阶条件,得到某一工业品j的消费量cj:
(8)
北部区域消费者总收入为E;H和L分别表示北部人力资本和工人的数量。北部企业的j产品在两个地区销售,即会有一部分产品运输至南部地区。根据新经济地理理论,企业产品在本地区销售不存在交易成本,但若在其他区域销售每一单位产品,会有τ-1单位产品在运输过程中被消耗掉。因此,北部企业的产出量为:
根据DS垄断竞争模型均衡时企业的净利润为零,因而产品价格为:
(9)
由于冰山运输成本pS=τpN,得到下式:
(10)
x=c+τc*为北部企业总产出,销售收入pNc+pSc*=pN(c+τc*)=pNx。当垄断竞争企业均衡时,其产品所得到的利润为零,此时可以得到公式:
pNx=TC=wH+(wLaM+tγ)xp=(wLaM+tγ)/(1-1/σ)
代入可得wH=pNx/σ。由于人力资本充当了资本的角色,此时所产生的经营利润实际为人力资本的报酬wH,由销售函数和工业品价格指数可得人力资本报酬函数:
(11)
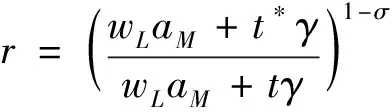
令θ=sn+φ(1-sn)r,θ*=φsn+(1-sn)r,b=μ/σ,则北部企业的利润函数为:
(12)
同样,南部企业的利润函数可以写成:
(13)
r为区域环境规制差异,由上式可知该参数为不定成本比例的线性变换。环境规制通过作用于r来影响人力资本报酬。这里假设北部地区环境规制强度更高,则r≥1。另一个需要注意的重要参数是贸易自由度φ,当φ=1时,表示贸易成本为0;当φ=0时,代表贸易成本为∞。Ew表示两地区的总支出即Ew=E+E*,sE代表北部地区支出份额,b是消费者消费工业品的份额μ和消费者偏好度σ的比值,人力资本报酬是随着b的增加而增加的。
工业部门的空间分布可以由人力资本的分布来表示,通过总支出等于总收入,可知给定人力资本的分布模式sH,进而得到市场份额的分布模式。由于总收入为Ew,即wLLw与企业家全体收入之和,总收入又等于总经营收入,即式(12)和(13)表示的企业经营利润的总和:
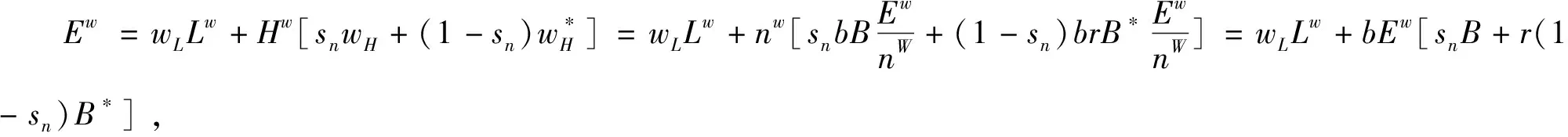
(14)
北部的支出可表示为:
E=SLwLLw+snnwwH=SLwLLw+bBEwsn
同时Sn=SH,所以:
(15)
而南部支出为:
(1-SE)=(1-b)(1-SL)+brB(1-SH)
(16)
由上面两式可见,市场份额与人力资本及劳动力的分布状态密切相关。
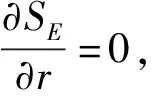
可见,在短期均衡条件下,如果人力资本分布保持不变,区域环境规制差异r的增加会使北部地区的市场份额减少。图1展示了不同环境规制差异下人力资本份额SH与市场份额SE之间的关系。
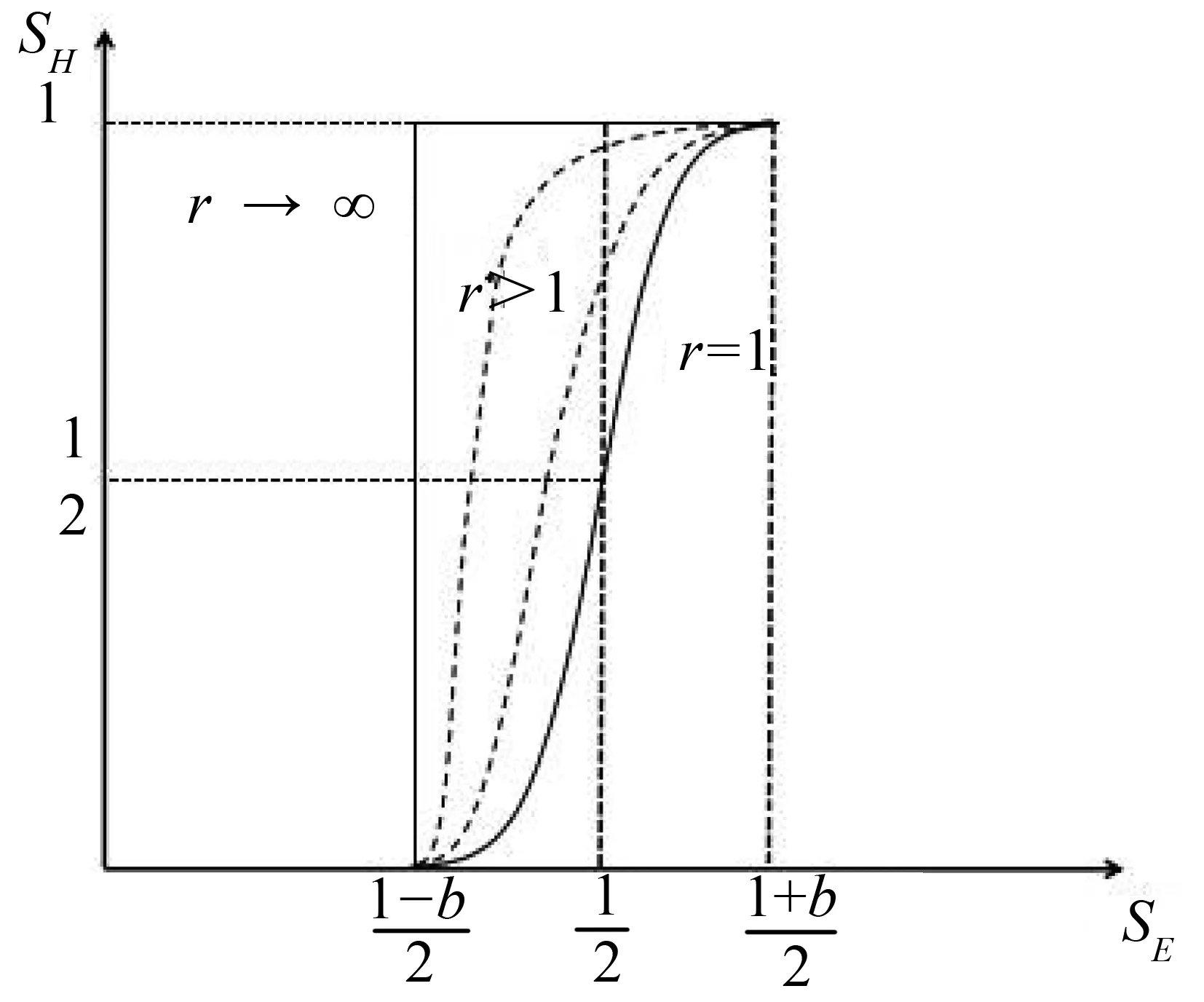
图1 不同环境规制差异下市场份额与人力资本份额的关系
(二)环境规制与产业集散效应
环境规制作为政府部门保护环境的管制手段,通过税收作用于企业,构成了企业可变成本的一部分,影响企业的收益和人力资本的收入水平,显然也会对产业集散效应产生不同程度的影响,进而影响产业空间分布。
1.本地市场效应
假设企业家选择企业所在地进行消费。当产业空间分布处于对称状态时(n=n*),人力资本从南部地区向北部地区转移。人力资源的转移会带动地区的消费支出,使得支出份额SE(北部地区)变大,假设唯一变量为贸易自由度,其取值范围为(0≤φ<1),市场规模的扩大使企业收入增加,从而带动人力资本报酬增加,促进地区的支出与规模的扩大。这一过程是自我强化的,被称为与需求关联的循环累积因果效应。
对市场份额(SE)求导得:
(17)
可见,随着市场规模的扩大,人力资本报酬也相应增加,存在本地市场效应。区域环境规制差异对本地市场效应的影响为:
(18)
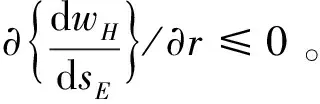
2.价格指数效应
生活成本效应又称为价格指数效应。当产业空间分布南北对称时,人力资本由南部地区向北部地区迁移,北部地区的人力资本数量及工业品种类的数目(sn)会增加。产品数量的增多将降低北部地区的生活成本指数,南部地区生活成本指数相对提高。人力资本不断向北部地区转移,这种机制不断强化,即为成本关联的循环累积因果效应(陶长琪,周璇,2015)[15]。
在两地区产业空间分布对称情况下,若不考虑本地市场效应和市场竞争效应,对北部地区实际工资取对数并进行微分:
(19)
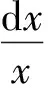
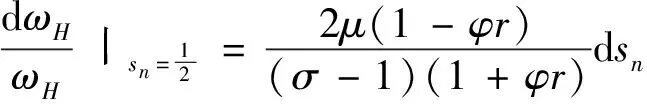
(20)
上式表明存在价格指数效应,且受到环境规制贸易自由度共同影响。令:
(21)
对区域环境规制差异变量(r)求导得到下式:
(22)
由式(21)可知,当φr<1时,价格指数效应为正,它强化了人力资本转移导致的实际工资的差异。同时随着r的增大,即区域环境规制差异增大,价格指数效应逐渐减弱。
3.市场竞争效应
为了区分生产转移与支出转移,FE模型假设人力资本的转移主要是由名义工资差异所致,且转移出去的人力资本收入返回原居住地的条件下,这时人力资本转移只改变sn,而不改变sE。从产业空间分布对称状态开始,当一部分人力资本由南向北转移,产业空间分布的均衡被打破,此时北部企业数目n增多,南部企业数目n*减少。这种趋势使得北部的市场显得更加拥挤,企业的消费者会减少,竞争也变得更加剧烈,北部企业经营利润下滑。为了保持收支平衡,企业将不得不支付较低的名义工资。同时,随着区域环境规制差异变量r的增大,北部企业的成本进一步提高,于是北部企业所能支付的名义工资又再一步降低,北部地区的吸引力下降,南部地区的人力资本不会再向北部地区转移。可见,这种扰动具有自我消除初始扰动之影响的能力。
人力资本报酬表达式(11)对人力资本份额sn求导可得:
(23)
由于通过数理公式的推导我们无法分析考察环境规制差异变量r的增加对式(23)的影响,因此,这里运用图解法即选取适当的数值代入其中,进行数值模拟分析。根据前述假设可以进行模拟参数的选择:μ=0.4,σ=5,SE=0.5,EW=nW=1,贸易自由度φ分别取:0.3、0.5、0.8,环境规制差异变量r分别取:1、1.3、2,通过Python可以作图如下(图2):
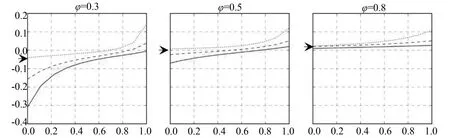
图2 不同贸易自由度与不同环境规制下dwH/dsn的图像
图2中实线、虚线和点线分别代表环境规制差异变量为r=1、r=1.3、r=2时dwH/dsn的图像。市场拥挤效应是由于人力资本集聚导致名义收入降低的过程,即dwH/dsn<0,在任一贸易自由度下,随着环境规制差异的增大,使dwH/dsn<0的人力资本份额范围越来越小,即市场竞争效应越来越弱。当其增大到某一程度后会发生dwH/dsn>0的情况,此时市场竞争效应消失。此外,由图可知,市场竞争效应的临界值与贸易自由度有关,即随着贸易自由度的增加,市场竞争效应消失时的环境规制差异变量临界值会越来越小。随着北部地区环境规制强度的增加,使得企业更倾向于转移至南部地区,此时北部地区企业份额的增加反而会提高当地的人力资本报酬,即区域环境规制差异增加会削弱市场竞争效应,直至市场竞争效应消失。
四、长期均衡及其稳定性分析
在对称FE模型中,两个区域的工人数量相等,即L=Lw/2,且人力资本具有空间流动性,其流动性是由人力资本的实际收入的空间差异所决定,人力资本H的流动方程为:
(24)
sH表示北部区域的人力资本份额,由于每个企业都只使用1单位的人力资本,因此人力资本份额也就是工业生产份额,即sn=sH。
当不存在人力资本流动时,经济系统实现长期均衡。由式(24)可见,有两种类型的均衡,第一种是内部长期均衡,这种均衡的条件是两地区的实际工资相同,且人力资本或企业没有完全集中在一个区域;第二种是核心边缘(CP)均衡,这种均衡是人力资本或企业完全集中在其中一个区域,其中又分为以北部地区为核心的核心边缘均衡(CPN)和以南部地区为核心的核心边缘均衡(CPS)。不同类型长期均衡的条件可写成:
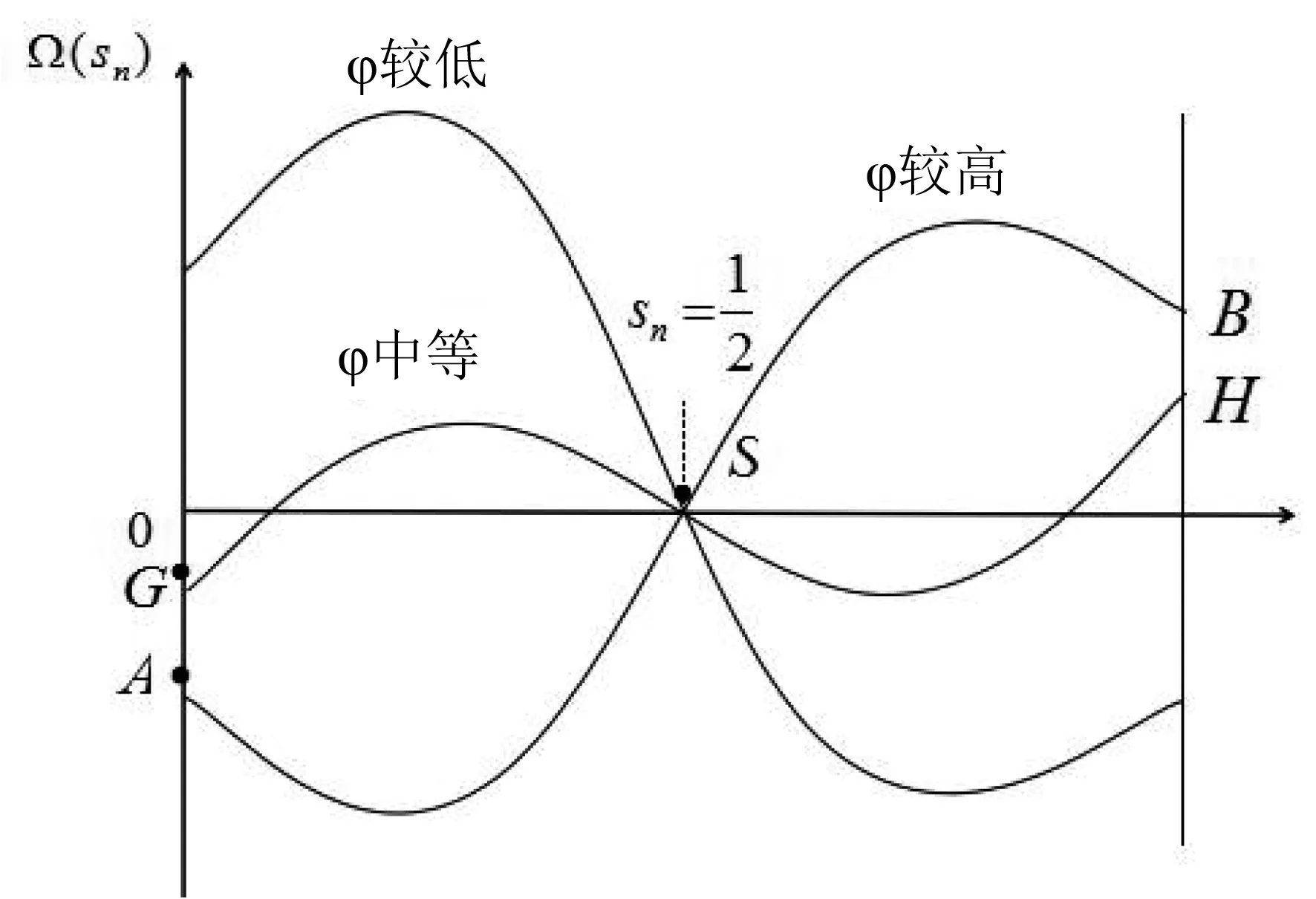
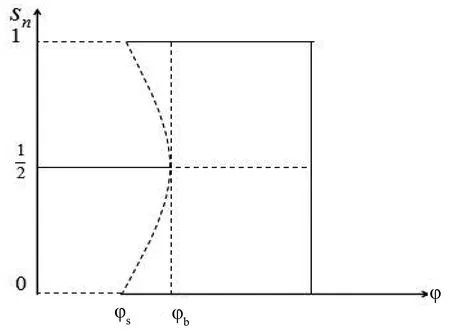
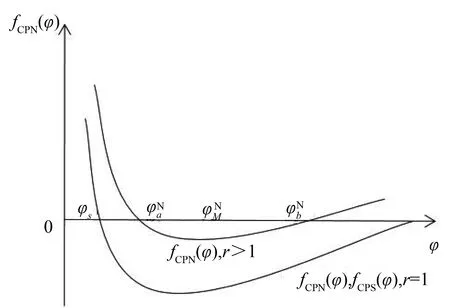
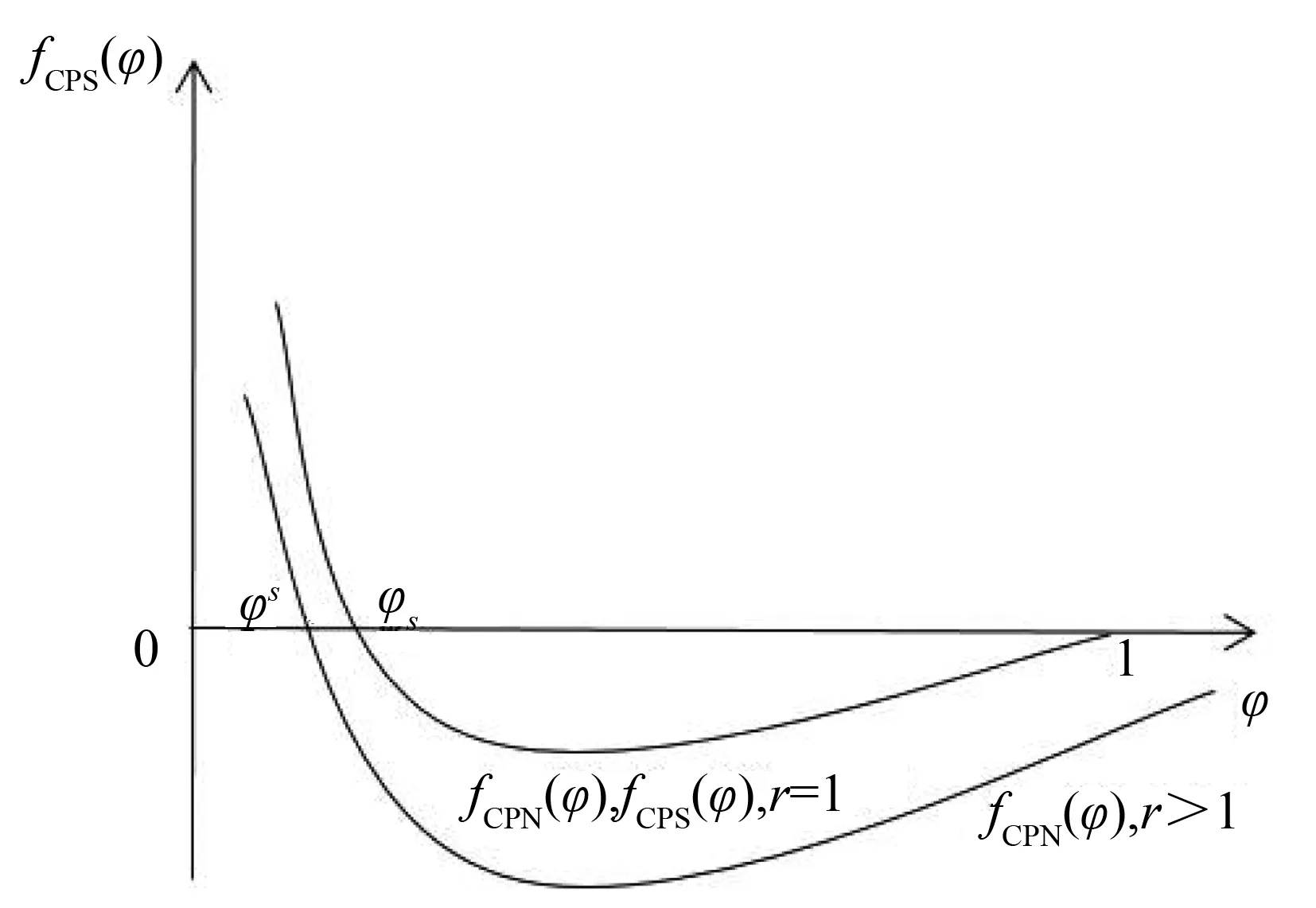
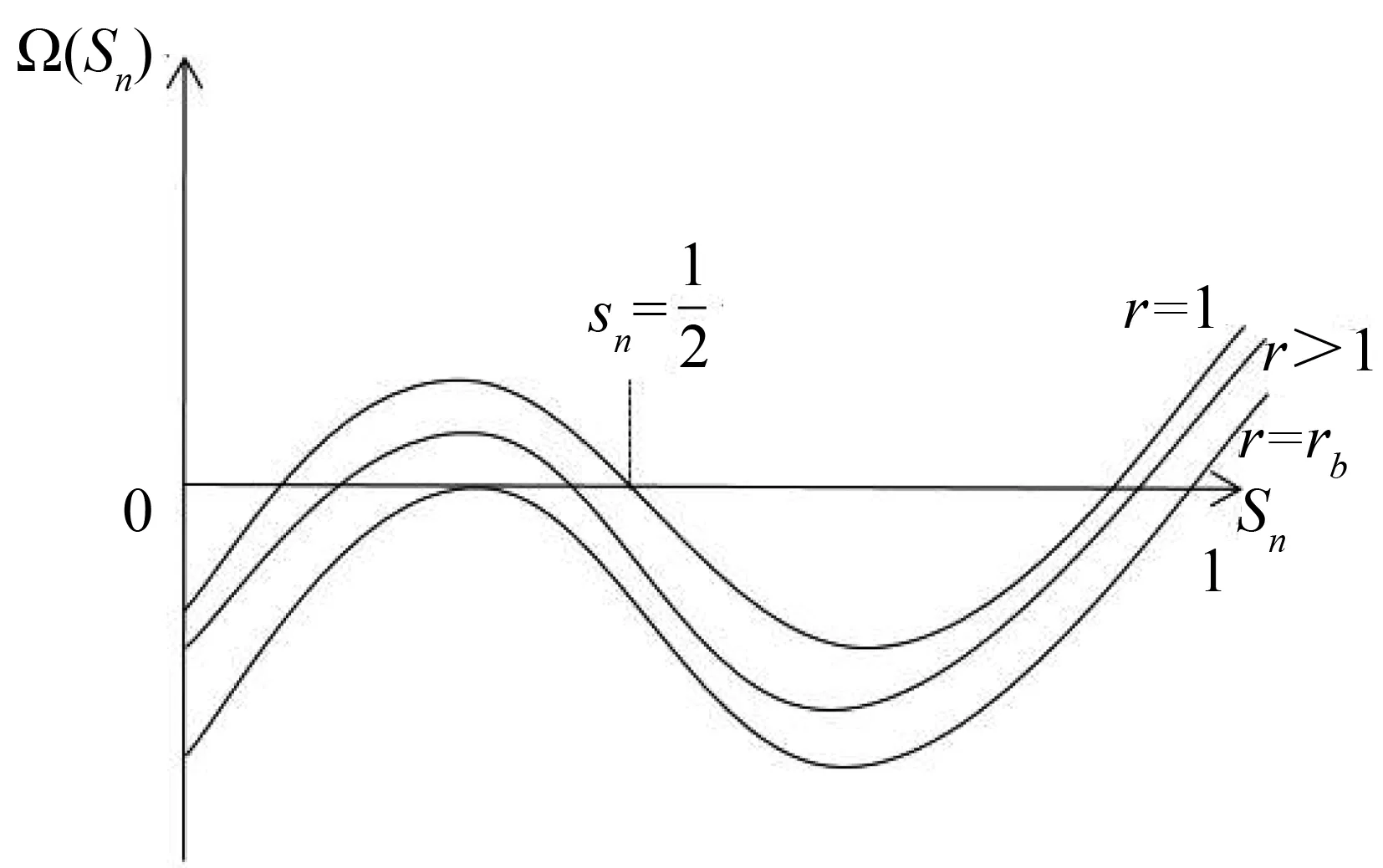
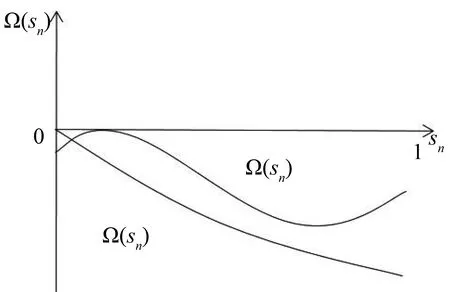
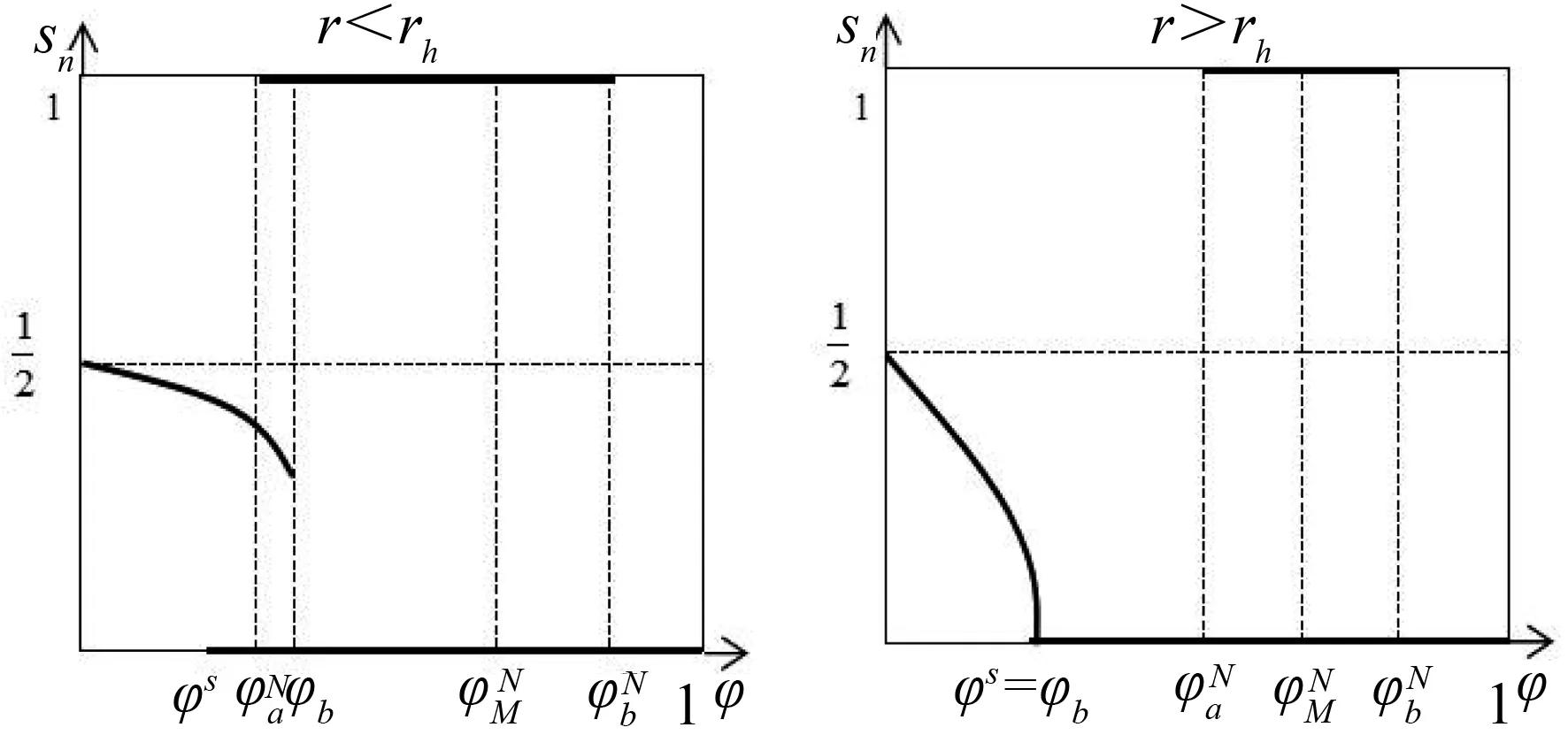
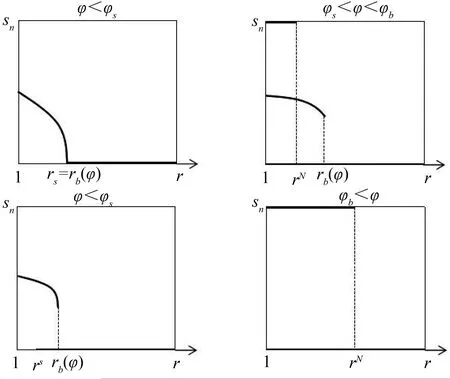
ω=ω*,Ω′(sn)<0当0 ω>ω*,当sn=1 (25) ω<ω*,当sn=0(我们用sn代替sH) 上式中的ω是实际收入,由于人力资本的实际收入涉及区域的生活成本指数,而生活成本指数中具有指数项,对实际收入比值取对数令其为Ω,则: (26) 当Ω>0(Ω<0)时,说明北方(南方)地区的实际工资更高。考虑到区域实施环境规制,需要结合均衡条件,进一步分析区域环境规制对均衡稳定性的影响。 图3 无环境规制情况下的摇摆线 南北两地区均未实施环境规制来约束企业的情况下,即t=t*=0,文中模型变为最基本的FE模型,实际收入比例的对数Ω变为: (27) 第一,对称结构均衡(sn=1/2)是唯一的内部长期稳定均衡。 第二,贸易自由度由φ=1减少时,均衡稳定存在三种情况:当贸易自由度高时,只有A、B两点的CP均衡是稳定的;当贸易自由度适中时,存在对称结构、以北部地区为核心和以南部地区为核心结构三种均衡稳定情况;当贸易自由度较小时,对称结构是唯一的长期均衡。 图4为FE模型的战斧图解。实线和虚线分别表示稳定和不稳定的长期均衡。长期均衡稳定性分析有两个关键的贸易自由度,一是突破点φb,即打破南北地区对称产业空间结构的临界点: 图4 FE模型的战斧图解 (28) 二是持续点φs,即CP模型保持稳定的临界点: (29) 当φ<φs时,对称结构是唯一的长期稳定均衡;当φ>φb时,核心-边缘结构是稳定的长期均衡;当φs<φ<φb时,对称结构、以北部地区为核心的核心-边缘结构和以南部地区为核心的核心-边缘结构分别为三个稳定的长期均衡。 当两地区实施有差异的环境规制条件下,区域环境规制对均衡稳定性影响不尽相同。不失一般性,本文假设t>t*≥0,也即环境规制差异变量r>1。 1.CPN均衡 以北部地区为核心的核心边缘结构均衡可以表示为Ω|sn=1,它的稳定条件由Ω>0来决定,变形后表示如下: (30) (31) 满足fCPN(φ)=0的贸易自由度φ是CPN均衡从稳定转变为不稳定的分界点。 考虑fCPN(φ)在r=1和r>1条件下的性质,作图如下(图5): 图5 r>1和r=1时fCPN(φ)的图像 (32) (33) 2.CPS均衡 以南部地区为核心的核心边缘结构均衡可以表示为Ω|sn=0,它的稳定条件是Ω<0,可以表示如下: (34) (35) 令fCPS(φ)=0的贸易自由度φ即CPS均衡由稳定变为不稳定的临界点。分析fCPS(φ)的性质,然后可以作出它的曲线图(图6)。 图6 r>1和r=1时fCPS(φ)的图像 当r>1时,fCPS(φ)=0在区间[0,1]上只有一个解,这说明与CPN均衡不同,CPS均衡由稳定变为不稳定的临界点只有一个。 对任意r水平,令fCPS(φ)=0的贸易自由度为φS,是CPS均衡的持续点,当φ<φS时,CPS均衡不稳定,当φS<φ≤1时,CPS均衡稳定。由图可见,当r增加时,CPS稳定均衡区间会包含更小φ值。 当r→,持续点φS→0,说明对于任何程度的环境规制差异(无论是由多大)一定存在φ使CPS均衡不稳定。若对于某贸易自由度φ下的CPS均衡不稳定,进一步可以求出,使CPS均衡稳定的最小环境规制差异rS为: (36) 3.内部长期均衡 首先,通过上述分析可知,函数Ω(sn)会随着环境规制差异变量r的增加而减少: 表明在短期内给定企业份额sn的情况下,不论是内部长期均衡状态还是CP均衡,实际收入的比率Ω(sn)是随着区域环境规制差异变量r的增加而减少的。根据FE模型,Ω(sn)函数的凹凸性最多改变一次,那么在非对称环境规制情况下Ω(sn)同样保持这个特性,如图7。 图7 不同环境规制差异下的Ω(sn)图像 可见,环境规制差异变量r的增加使函数Ω(sn)下降,但是这种下降并不是均匀的,环境规制差异会影响Ω(sn)取得极值时的sn。据此,可以总结内部长期均衡稳定状态的相关特性: 第一,当环境规制差异变量r增加至某一值时,对于任何贸易自由度φ>0,r再增加就会使Ω(sn)继续下移,长期均衡不会稳定,rb没有显性解。 第二,当内部长期均衡稳定时,由于环境规制差异变量r>1,两地区的企业份额变得不相等。当核心边缘均衡时,区域环境规制差异微弱的变化不会引起企业转移;而内部长期均衡状态时,任何环境规制差异的变化都会引起企业转移。 第三,当内部长期均衡处于稳定时,区域环境规制差异变量r增大超过rb时,形成产业集聚,内部长期均衡不再稳定,表现为突发式与渐进式两种形式。 进一步考虑贸易自由度对均衡的影响,存在贸易自由度φb作为突破点。当φ>φb时,内部长期均衡不再稳定。然而在区域环境规制差异变量r>1的情况下,突破点成为环境规制差异变量r的函数,即φb(r)。也就是说,当贸易自由度φ在0和φb(r)之间时,内部均衡稳定,其中北部地区企业份额sn∈(0,1/2),如果φ>φb(r),内部均衡不再稳定。 考虑环境规制差异变量为r1,此时贸易自由度刚好为突破点φb(r1),处于内部长期均衡稳定状态,当环境规制差异略微增大至r2(r2>r1),使Ω(sn)在贸易自由度仍为φb(r1)情况下,此时φb(r1)>φb(r2)。可见,φb(r)随着r的增大而减小。 考虑贸易自由度处于内部长期均衡突破点的情况φ=φb(r),此时Ω(sn)函数的极大值点分为两种情况:第一,极大值点sn>0,Ω′(0)>0;第二,极大值点sn=0,Ω′(0)≤0,即代表产业集聚的两种情况,突发式和渐进式。如图8所示,这两种情况下的环境规制差异变量分别为ra和rb。 图8 当贸易自由度φ=φb(r)时突发式和渐进式转移的摇摆线 进一步分析区分突发性产业集聚和渐进性产业集聚的区域环境规制差异变量r的临界值。具体来说,是由在某个环境规制差异变量r下,Ω′(0)|φ=φS的符号决定的,φS是CPS均衡稳定的持续点。考虑贸易自由度由0变为1的过程,当Ω′(0)|φ=φS>0时,此时区域环境规制差异下的内部均衡突破点φb(r)是大于持续点φS的,此时产业集聚由内部均衡向CP均衡的转变是突变式的;当Ω′(0)|φ=φS≤0时,区域环境规制差异下的内部均衡突破点φb(r)是等于φS的,产业集聚由内部均衡向CP均衡的转变是渐进的。将Ω′(0)|φ=φS=0时的环境规制差异变量标记为rh。下面两图即为环境规制差异变量r和贸易自由度φ对均衡稳定性的影响。 图9 环境规制差异r>1情况下的战斧图解 图10说明了四种贸易自由度下环境规制差异对产业集聚的影响。左侧两图描述了在贸易自由度小于无环境规制情况下r对均衡稳定性的影响。此时内部均衡向CPS均衡过渡的形式有两种,上图表示的是内部长期均衡平缓过渡到CPS均衡的情况,下图表示的是突变式的企业转移。右上图是贸易自由度在φs<φ<φb区间时,内部均衡向CPS均衡过渡是突变式。当环境规制差异r=1时,内部长期均衡和CP均衡都是稳定的,而随着r的增大,CPN均衡不再稳定,内部长期均衡在逐渐变得不稳定。右下图贸易自由度φ>φb,此时在r=1时,只有CP均衡才是稳定的,随着r的增大,CPN均衡逐渐变得不稳定。 图10 不同贸易自由度下均衡稳定性与环境规制差异变量r间的关系 短期中,当北部地区的环境规制强度低于南部地区时,北部地区的本地市场效应的强化机制并不会减缩;当北部地区环境规制强度高于南部地区时,由于北部是个大市场,在短期内环境规制强度增强引起的分散力并不会超过本地市场效应引致的聚集力。因此,尽管环境规制差异会弱化本地市场效应和价格指数效应,不利于人力资本的进一步转移(李胜兰等,2014)[16],但还足以导致北部地区产业向外转移。长期中,以北部地区为核心的长期均衡(CPN)稳定的范围在缩减,环境规制强度较弱的欠发达地区更倾向于形成产业集聚。 综上所述,环境规制和产业集聚之间呈现倒U形特征,说明在短期内环境规制的实施并不会引起北部产业转移,此时的聚集力大于分散力;随着环境规制强度进一步增强,企业生产成本上升,北部地区拥挤效应所形成的分散力要大于本地市场效应所引致的聚集力,北部地区的企业会逐渐向南部地区转移。 近年来,随着我国经济的发展,环境污染的问题逐渐严重,随之而来的治理问题也使得我国各地的环境规制不断增强。本文在“新”新经济地理学模型框架下,通过从分税制下区域环境规制异质性出发,研究了环境规制影响产业空间分布均衡的内在机制。在短期中,区域环境规则异质性会减弱本地市场效应和价格指数效应,不利于人力资本流动。环境规制强度高的地区名义收入会降低,市场竞争效应引起的产业分散力会增强。由于北部地区拥有较大市场,环境规制强度增强引起的分散力在短期并不会超过本地市场效应引发的聚集力,因此,尽管环境规制差异会弱化本地市场效应和价格指数效应,不利于人力资本流动,但是北部地区环境规制的变化强度还没有使得北部地区的企业向外转移。长期中,在区域环境规制差异一定的情况下,贸易成本处于高水平和低水平时,产业集聚更倾向于发生在环境规制强度较弱区域。以北部地区为核心的长期均衡(CPN)稳定范围在缩减,区域环境规制异质性与产业集聚存在倒U形关系,这使得随着区域环境规制异质性的增强,将对区域产业空间分布产生广泛的影响。此外,环境规制与贸易自由度综合作用可以引致产业空间稳态的变动。 本文研究的政策启示在于:第一,长期来看,区域间环境规制异质有利于促进产业集聚,实现区域经济一体化。欠发达地区通过环境规制保护区域生态环境的同时,还可以为产业聚集形成和发展创造良好的外部条件,实现“绿水青山就是金山银山”。第二,在现有的环境规制强度下,应该以发展绿色经济为出发点,使得产业分工与绿色发展相协调,实现环境规制对地区产业集聚抑制最小化。第三,制定适度的环境规制不会影响地区产业集聚,环境规制强度需要根据经济发展与区域环境状态进行灵活调整,从而提高产业集聚效应。 诚然,本文使用的“新”新地理学框架的两地区两部门假设,忽略了多地区情形下厂商及地区之间错综复杂的竞争及共谋行为,这会影响对于国外国内环境规制下对正负外部性影响的内在差异,进一步放松假定条件来深刻理解现实中制度对区域发展的影响,这是本文未来的研究方向。(一)无环境规制下的稳定性分析(图3)
(二)区域环境规制差异下的稳定性分析
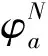
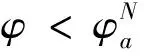
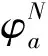
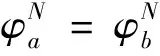
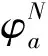
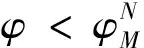
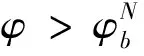
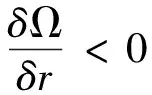
五、简要结论
六、结论和政策建议
