清代前期的交通成本与粮食市场整合的再估计——基于第二次金川之役自然实验的量化考察

何石军 蔡 杨 高 明

（1.武汉大学经济与管理学院 湖北武汉 430072）

（2.西南财经大学经济学院 四川成都 611130）

（3.西南财经大学经济与管理研究院 四川成都 611130）

一、引言

自从亚当·斯密揭示专业化分工和贸易会促进财富增长以来，从市场发育的程度来解释国家或地区经济增长的表现差异就成为一种重要视角（Chilosi等，2013）。这种专业习惯在研究中西大分流的问题上表现得尤为明显：如彭慕兰（2010）利用各种史料和前人的研究定性地比较了中西方在工业革命前夕的市场表现，发现两者并无太大差异；Shiue和Keller（2007）则利用粮价数据，利用协整等方法对比工业革命前夕东西方的市场整合情况，发现两者的粮食市场发育程度相近。然而更深层次的问题是，决定市场发育和整合的基础因素是什么？正如Evans（1984）所说，决定市场整合的深层次原因是交通成本。

显然，在基本的制度给定之后，交通成本对决定两地之间是否贸易具有至关重要的作用（Glaeser和Kohlhase，2003）。因交通成本的下降而产生的套利空间使原本处于自给自足的两地出现商品和货物流通，促使市场发育和整合，进而推动经济增长（O’Rourke和Williamson，1999）。这促使众多学者试图从交通成本的角度去理解前现代社会的市场发育和整合情况，进而去理解中西方的经济发展差异和大分流问题。这比单单讨论市场整合能给我们提供更多洞见（Evans，1984）。大量研究对交通成本进行了估计，这些估计方法大致可以分为三种：间接法、直接法和价差法。

间接法是通过对比交通技术、市场整合程度来间接推断交通状况及其成本差异。彭慕兰（2010）比较了工业革命之前中国和欧洲的役畜使用情况，认为较多的役畜给欧洲带来了陆路运输方面的优势。Shiue（2002）利用粮价数据，从两地粮价相关系数大小估计出内陆地区的贸易联系只限于800公里以内，水运较发达地区的贸易联系可达1 100公里，沿海地区的贸易范围可达1 500公里，并认为这种差异是由于水路和陆运交通成本的差异导致的。这与颜色和刘丛（2011）的发现一致，即在 18世纪的中国，水运更发达的南方市场整合优于北方。这些研究都指出交通成本的大小与市场整合程度密切相关，并指出了受交通成本影响的市场整合的范围。两个市场间的交通成本随着距离的增加而增大，并导致了较低的市场整合程度。然而这类研究无法直接估计交通成本。因此，为了更精确和直接的比较，我们需要对交通成本进行更具体的估计。

估计交通成本的直接法是指使用史料直接去估计人力、畜力和交通工具等与交通相关的各方面成本，进而加总得出一个总成本。一些学者基于私人运输数据计算交通成本：Buck（1937）发现在20世纪上半叶的中国，担70至80磅的搬运工长距离的成本是1.62元每吨每英里，帆船则是0.39元。另一些学者基于官方规定的标准人力、畜力和交通工具消耗计算出相应的成本：Evans（1984）估计沿北京的陆路运输25英里的成本是每石0.125盎司白银，而从重庆到苏州1 400英里的距离每石只需0.65盎司成本，以此估计陆路成本是水路成本的11倍。①0.65盎司陆路能够把一石粮食运送125英里，而长江的水路可以运送1 400英里，因此陆路成本与水路成本之比为1 400∶125，约为11倍。但是这种直接以货币度量的交通成本估计方法忽略了两地贸易间的制度成本、时间成本以及风险因素等，也没有考虑到交通成本跟商品价格的关系。正如Evans（1984）指出的，如果以金钱成本度量，北京附近的陆路交通成本是长江水路成本的11倍，然而考虑运费占粮价的比例，实际的比例是1.5—5.5倍。

另一些学者则用价格差方法，比如通过估计两地粮价差来推断交通成本。②假设起始地的价格为p，目的地的价格为p*，单位交通成本是f，如果两地因贸易得到均衡，那么p*=p+f，由交通成本导致的价格加成百分比是p*/p-1=f/p,参见Hummels（2007）。Chuan和Kraus（1975）认为在1723—1735年社会相对稳定的条件下，相对价格差异是可以比较好地反映交通成本的，他们估计在长三角地区价差以每英里0.03%的速率变化。也有一些学者同样基于粮价差并使用了更复杂的计量模型来估算两地之间的交易费用（彭凯翔，2015）。这种估计都是基于市场整合定义或者一价定律：若存在甲、乙两个市场，若甲地价格上涨，并且两地间价格差超过了乙地至甲地的交通成本，就会产生跨区域的套利行为，即乙地的商品流向甲地，直到两地的价差等于交通成本为止。这一估计方法的好处是可以充分考虑到两地贸易的制度成本、时间成本以及风险因素等，给了我们一种很好的思路。

因此，本文也利用价格差来估计交通成本，但与已有研究不同的是，本文利用自然实验带来的价格差来估算交通成本。我们基于市场整合的定义推断：如果一个外生冲击使得中心市场价格上升，若一定区域内存在市场整合，那么我们就可以观察到各地区到中心市场的距离与价格成反比的现象。通过估算单位距离内的商品价格差，便能得知单位距离内交通成本的大小，进而估计市场整合范围。

1771年至1776年，川西高原爆发了第二次金川之役，交战的双方分别是清军与大、小金川土司。清军在前线对粮食的巨大需求造成了四川省粮食价格的大幅上涨（上涨的情况见图1）。这场冲击以成都为中心市场，并带动整个四川盆地粮价上涨。第二次金川之役的冲击，是一次很好的利用价格差来估计交通成本的自然实验。本文利用自然实验估计交通成本具有多方面的优势：第一，能够克服只用两地价差估计交通成本的时间点选择问题；第二，能够控制其他冲击导致的价格差；第三，能够避免向量自回归模型带来的两地价格此消彼长的问题。

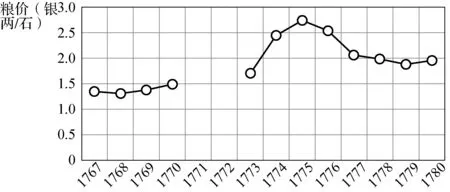
图1 四川省中米年平均价格，1767—1780年

基于此次自然实验，我们利用双重差分方法估计了单位距离上的交通成本，发现每百公里陆路交通成本大致是粮价的2.61%，每百公里水路交通成本大致是粮价的1.47%。我们进一步估计了旱涝灾害引起的市场整合的范围，发现陆路运输和水路运输可分别将旱涝灾害的影响扩散至距离冲击中心大约380公里和680公里的范围。也就是说，旱涝灾害的影响通常不会超过一个区域市场的范围，这一发现与施坚雅（2000）的观点比较吻合。

文章结构如下：第二部分提出一个简单模型，并对第二次金川之役作简要介绍；第三部分是数据介绍和描述性证据；第四部分基于前文提出的模型，使用双重差分方法对交通成本进行估计；第五部分基于估计的水路和陆路交通成本，对旱涝灾害引起的市场整合的范围进行了讨论；最后是总结。

二、假说与历史背景

（一）假说

我们假设一个局域有n个地区，每个地区都有一个粮食市场，市场i在时期t的粮食价格为Pit，并且存在一个中心市场c。初始状态下，各地市场处于均衡状态，价格Pit=αi+θt，其中αi和θt分别表示由个体和时期特征决定的价格。中心市场的价格为Pct=αc+θt。

如果在t+k时刻，中心市场的价格突然上涨H，此时c的价格为Pct+k=αc+θt+k+Ht+k。①Ht+k 可以被时间固定效应θt+k 吸收，但是这里为了示意冲击的大小便单独列出。由于各地的粮食市场是整合的，根据一价定律，其他市场的粮食就会流向中心市场，或者流向更靠近中心市场的市场，直到价差等于两个市场间的交通成本为止。也就是说，其他地方的价格应为Pit+k=αi+θt+k+Ht+k-β×distancei，其中distancei表示i市场到中心市场的距离。如果我们定义一个变量D，如果在t+k时刻D=1，其他时候D=0，那么就可以用下式表示任一市场、任一时期的价格：②DHt 可以被时间固定效应θt 吸收。

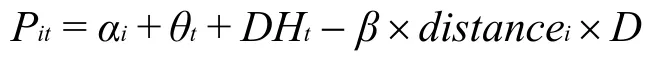
我们可以看到，各市场的价格要呈现上式的模式，需要有一个中心市场的价格上涨，并且各地存在市场整合。其中β表示受到外生冲击时，单位距离所产生的价格差，即交通成本。因此，如果我们能够找到一个存在一个中心市场价格外生上涨的自然实验，就能通过上式来估计交通成本的大小，进而说明市场整合的范围。

（二）历史背景

基于假说的描述，历史背景的阐释分两部分展开。首先是阐述第二次金川之役爆发的原因，在这一部分我们可以看到战争是基于政治和军事原因而爆发的；其次是阐述军需的运输，在这一部分我们可以看到粮食补给主要是基于市场行为，并且粮食是从四川各地汇集到中心市场成都然后运往前线。两方面的结合为我们提供了估计交通成本的历史契机。

大小金川是清代嘉绒藏族十四土司之二（促侵和儹拉）。1770年大金川土司朗卡去世，土司职由其第四子索诺木承袭。1771年，索诺木夜袭革布什咱，杀害了革布什咱的土司并占领了官寨。大金川的行为鼓舞了小金川土司僧格桑，后者相继攻袭沃日、明正和革布什咱土司。这激怒了乾隆皇帝，他认为“不加惩创，伊等将视内地大臣专务调停和事，不复知所畏惧”。①《平定两金川方略》第5卷，第18页。8月，乾隆宣布派五千名士兵前往镇压，第二次平定金川之役打响了。

1771年11月，清军分西、南两路进攻小金川。西路由成都出发，南路由雅州出发。1773年1月清军攻破小金川，僧格桑逃亡大金川投靠索诺木。接着，清军分为三路进攻大金川。1773年7月清军被大金川击败，阵亡将士4 000多人，小金川得而复失（彭陟焱，2010）。清军重新整顿后，于同年12月仅用十天就复克小金川。乾隆帝继续增派兵员，此时共计调兵8万余人（彭陟焱，2010）。1774年2月清军分三路征剿大金川，于1776年3月全境荡平大金川。第二次金川之役历时四年零七个月，乾隆先后调兵129 500余人。②《平定两金川军需例案》，第5页。

“兵马未动，粮草先行”，后勤补给是事关战争成败的最为重要的因素之一。在第二次金川之役中，补给线由西路和南路构成。两条补给线基本与清军的进军路线重合。1773年西路又开辟了一条新的运输路线，由于这条线路更加便捷，因此后期大部分补给都是通过这条路线实现。西路由成都出发，成都位于盆地西缘，毗邻川西高原。它在战时成为后勤供给路线的枢纽，来自四川盆地的粮食、衣物、武器汇集至此，进入高原。

清政府组建了临时的后勤网络，由设在成都的“军需局”统一管理，每条路上设一个主要管理人员。在这两条运输道路上，每30里至50里设置一些粮站，一些叫作“里夫”或“背夫”的劳力，负责在不同的站之间运输物资。清政府总共动员约462 000名劳动力③同上。，主要用于后勤保障和运输物资等工作，其中运送粮食需要大量人力。来自四川本地的劳动力大约有150 000多名（Dai，2001），由于这些劳力不能满足运输需求，因此政府还大量招聘外省劳动力——“客夫”。客夫占了三分之二以上的人数，而且由于本地人可以出钱雇用外地人顶替自己，实际外地人所占比例更高（Dai，2001）。这套运输系统叫作“正运”。他们由政府雇用来运输物资，能获得很高的报酬，正如乾隆所说的“宽裕优渥”④见《清高宗实录》第321卷，第45页。。

然而由于清朝行政系统规模较小，要依靠“正运”系统进行物资运输十分困难，因此他们借助市场，委托商人采购粮食并运送至指定地点。⑤由商人运至前线指定目的地的米，被收购的价格一般在8.5—15两每石，高的时候可以达到20—23两每石。因此，商人有很大的激励把米运送至前线，参见Dai（2001）。这一运输方式叫作“商运”。相对于正运，商运有多方面的优点：首先，免除了政府征召劳动力的麻烦，这通常是吃力不讨好的事情，特别是在乾隆帝三令五申不得强抓“壮丁”的情况下①比如，乾隆帝要求“不得官为勉强，不得稍涉张皇，并严禁胥役借端勒索。总期于事有益，而于民无忧”，参见王纲（1992），第1503页。；其次，商运减少了运送至前线粮食的损耗，正运因为要给劳动力口粮，以至于运送至前线的粮食通常会消耗一半以上。由于这些优势，商运逐渐地替代了正运。当时总督富勒浑甚至认为“官雇人夫完全无用”，主张放弃。②《金川档》，第三十九年，第1卷，第229页。清军的粮食主要靠商运保障，整个第二次金川之役运送粮食296万石，其中264万石是通过商运完成的。③《平定两金川军需例案》，第5页。这场战争总共花费户部银6 160万两④同上。，商运耗银3 228万两⑤《平定两金川军需例案》，第168页。，超过总数的50%。⑥军队后勤市场化的运作方式还体现在政府没有实行价格管制上。Dai（2001）发现商人从四川盆地运往前线的米上涨了5—10倍，但政府并未对此干预；又如1774年四川总督富勒浑等曾向乾隆帝汇报了买米的计划，认为“如果将现在急需的六万石米迅速买齐，会造成运输工人工资和米价飞涨，不如像之前那样买米，保证工资和米价相对稳定”（原文见参见王纲，1992，第1685页）。这句话从侧面反映了政府没有直接干预工资和粮价。政府像一个典型的微观经济主体那样，面对工资和价格变化，也只能调整自己的购买计划以节省支出。此外，政府接受的捐纳也不破坏市场机制的运行。原因在于，如果捐纳的是粮食，那么这些粮食肯定不是民间富人通过行政手段获得的；如果捐纳的是钱，那么政府获得这些收入后也是采用市场化的运作方式采购物资的。

在第二次金川之役中，清朝采取了高度市场化的军队后勤运作方式。这既表明当时整个经济高度商业化，也表明了政府利用国民资源的理性化。这种市场化的运作方式使得交通成本被理性和前瞻性地考虑进来。因此，第二次金川之役是一次良好的自然实验，提供了一次很好的估计交通成本以及受此约束的市场整合范围的机会。

三、数据介绍与描述统计

（一）数据介绍

根据前文的假说，我们会对外生冲击发生时，区域内中心市场和其他市场的价格差进行估计。因此，在回归中涉及的变量主要是粮食价格和到冲击中心的距离。

首先，粮价数据来自台湾“中研院”的《清代粮价资料库》，该数据库摘抄自粮价单。⑦《清代粮价资料库》，http://mhdb.mh.sinica.edu.tw/foodprice/。此数据库提供了四川省23个府的中米月度价格。由于一些地区可能会受到战争的直接冲击，政府也可能不会在一些偏僻地区采购粮食，故本文在回归中将川西北的松潘、茂州、龙安、宁远和川东南的酉阳、石砫剔除。本文回归中府的数量保持在17个。⑧虽然雅州府大部分辖区位于川西高原，但其府城海拔仅581米，故予以保留。本文提到的四川省平均价格均是指四川省23个府的均价，但本文的实证研究只关注其中17个府。本文对这17个府同一年中12个月的数据进行算术平均得到中米年平均价格。

本文涉及的距离包括陆路距离和水路距离。其中陆路距离来自杨正泰（2006），该书附有《一统路程图记》。《一统路程图记》提供了从成都出发的两条主干道的里程数据。对于少数不在主干道上的府，本文采用杨正泰（2006）提供的《四川驿路分布图》作为补充。①《一统路程图记》，第195—292页；《四川驿路分布图》，第123页。《四川驿路分布图》提供了成都至各府的驿站数量。以每站30公里计，本文计算出成都到其余府的距离。各府到成都的水路距离来自CHGIS（2007），该系统提供了1820年各府城的经纬度数据和河流里程数据。本文在此基础上计算出四川省其他地区到成都的水运距离。回归中距离的单位是100千米。

在稳健性检验中，我们还考虑了天气的影响。短期内天气无疑能造成粮价的剧烈波动，本文的天气数据来自《中国近五百年旱涝分布图集》（中央气象局气象科学研究院，1985），该图集将旱涝情况分为五级，对应的数字编码为1、2、3、4、5。数值越大，表示降雨量越小。“天气”变量的设置方法为：若旱涝等级为1、2、4或5级，则该变量取值为1；反之，该变量数值为0。本文将距离每个府最近的观测点的旱涝等级作为该府天气的代理变量。此外，我们还考虑了人口和海拔等因素。本文的人口数据来自曹树基（2001）提供的四川省各府1776年人口数据。府城的海拔高度来自Google Earth Pro。

（二）描述性统计

根据前文的假说以及对历史背景的描述，我们定义1773—1776年为战争年份，并取1767—1771年（战前四年）和1777—1780年（战后四年）作为非战争年份。②因为1771年和1772年粮价数据缺失严重，故回归中不包括这两年。表1的Panel A是本文所使用变量的描述性统计。Panel B将全部17个府按照陆路距离和水路距离分别从小到大排序，并分成两类：陆路（或水路）距离前50%的府（8个）和陆路（或水路）距离后50%的府（9个），并汇报了各地区在各时间段的均值。总体而言，战时的粮价均大于战前战后的粮价，并且战时粮价最高的地区是陆路距离和水路距离都比较小的地区。

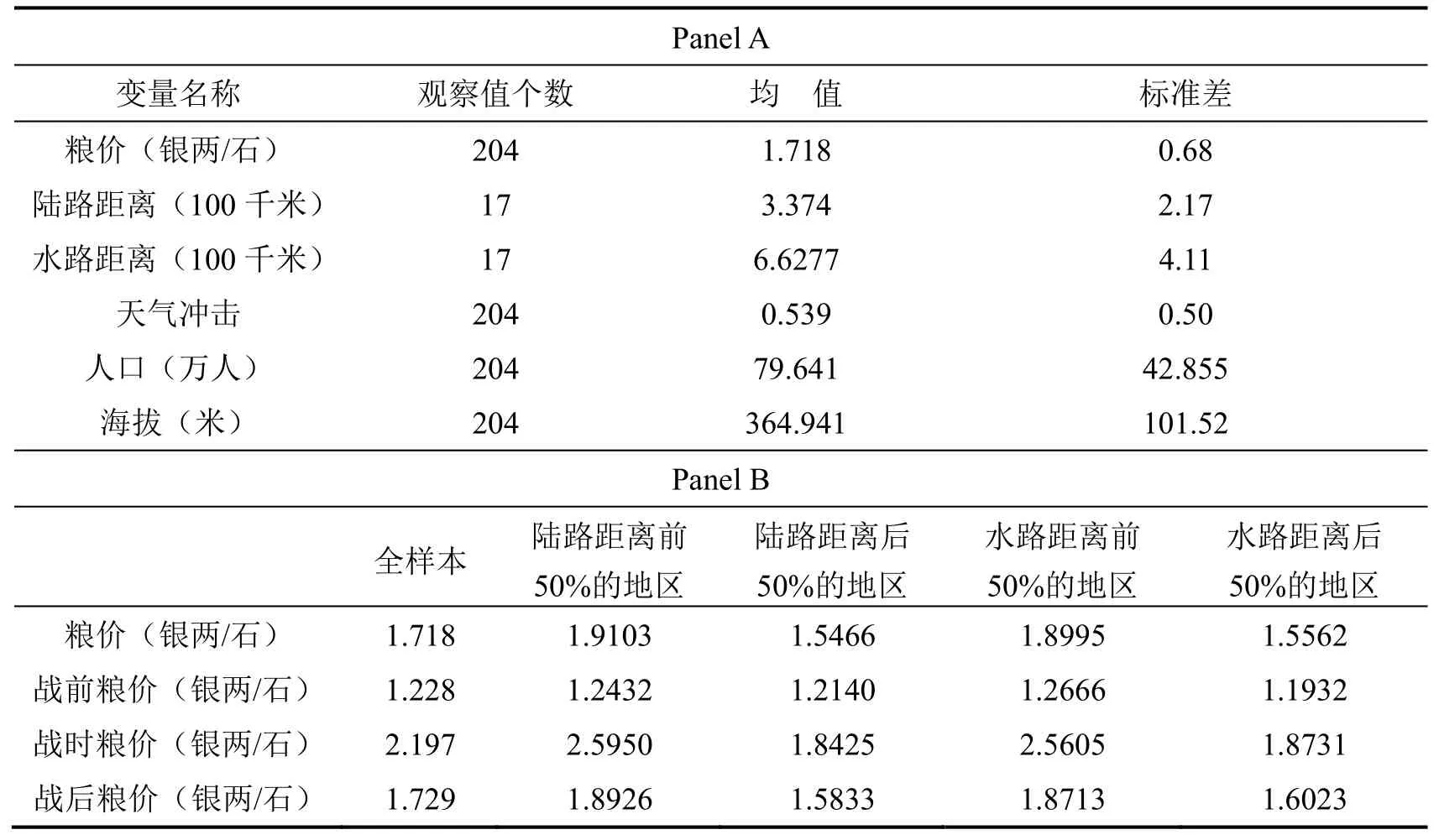
表1 描述性统计

四、回归结果

（一）基本回归结果

根据前面的假说，我们采用双重差分模型估计交通成本。基本回归方程设定如下：

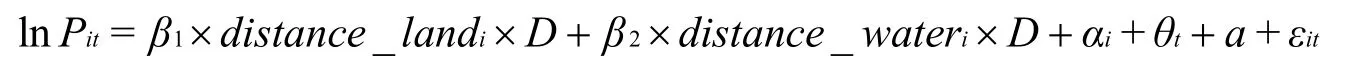
其中，被解释变量lnPit是第i个府在t年的粮食价格（中米年平均价格）的自然对数。粮价取对数的原因是，战争期间付给运输工人的工资必然会受粮价影响，因此通过取对数，我们可以得到一个类似交通费用占粮价百分比的度量。distance_landi和distance_wateri分别为i府至成都陆路距离和水路距离。D是表示战争是否发生的虚拟变量，该变量的定义为：若某年是战争年份（1773—1776年），则D=1；若某年是正常年份，则D=0，包括战前四年（1767—1770年）和战后四年（1777—1780年）。因此，β1和β2的绝对值就是本文所关注的陆路和水路交通成本的大小。αi为个体固定效应，θt为年度固定效应，a是常数项，εit是随机扰动项。表2汇报了基本回归方程的估计结果。

表2中第一、二列分别将陆运距离与D的交互项和水运距离与D的交互项作为解释变量，第三列将两者同时纳入回归方程。从表2中可以看到，回归结果与我们的假说一致：交互项的系数都是显著的负数。这反映了价格差或交通成本与距离成比例的现象。具体来说，第一列回归结果显示，在战争年份到成都府的陆运距离每增加100千米，粮食价格平均下降4.37%；第二列回归结果显示，在战争年份到成都府的水运距离每增加100千米，粮食价格平均下降2.31%。由于同时存在陆路和水路运输，第一、二列回归系数的绝对值可能被高估。因此，将两个交互项同时纳入回归方程后（第三列），两者的系数的绝对值都有下降，陆路每百公里交通成本为粮价的2.61%，水路每百公里交通成本为粮价的1.47%，陆运交通成本是水运交通成本的1.78倍。

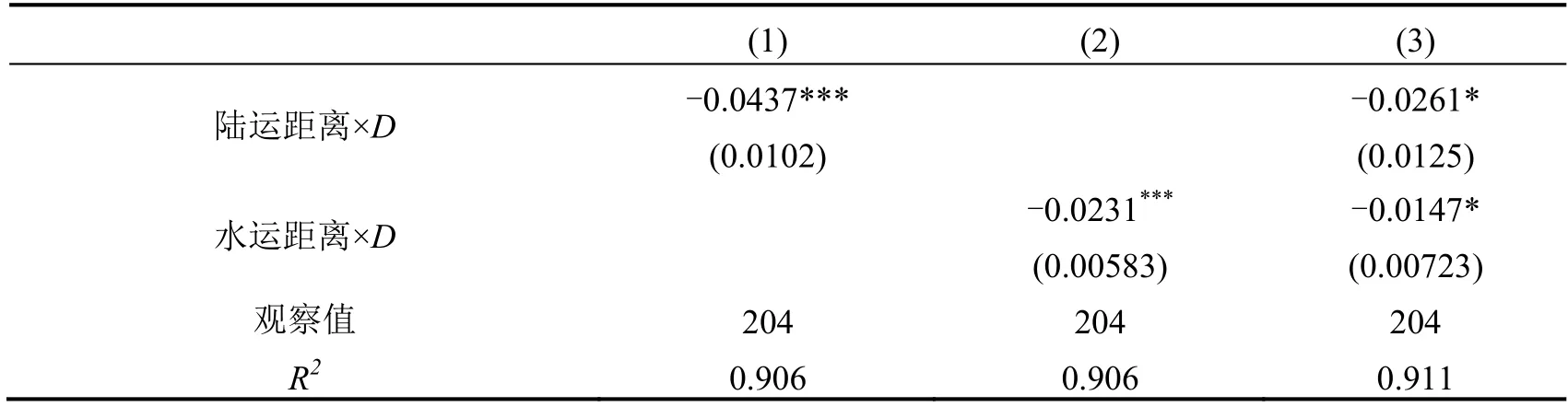
表2 基本回归结果

（二）共同趋势检验

虽然表2中第三列的回归结果已经不是标准的双重差分模型了，但我们仍有必要进行共同趋势检验。具体而言，共同趋势存在是指在没有战争冲击时（即战前和战后），距离与粮价的关系与基年基本相同或没有显著差异。共同趋势检验的回归方程如下：

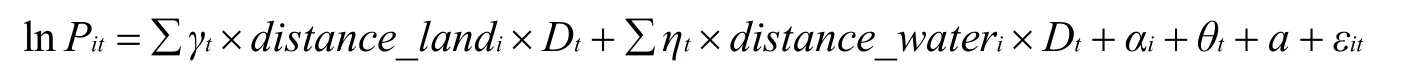
此时Dt表示以1767年为基年的各个年份的虚拟变量。因此，γt和ηt表示与基年相比，各年份中陆路距离和水路距离与粮价的关系是否存在差异。图2汇报了共同趋势检验的结果，γt和ηt在战前（1768、1769和1770年）都基本不显著，但是在战争发生后，系数由不显著变为显著为负。图2的检验结果较好地满足了共同趋势假定。

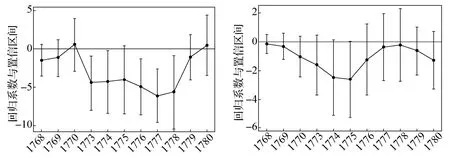
图2 共同趋势检验

（三）稳健性检验

1.增加变量的回归

根据前文的假说，外生冲击发生时到成都的距离决定各府的粮价。但是，也必须考虑天气以及各府其他可能影响粮价的特征。本文加入天气及人口、海拔与时间趋势的交互项以增强回归结果的说服力。回归结果如表3所示。表3的结果表明上述变量不影响基本回归结果：陆运距离×D和水运距离×D的系数均是显著的负数，其数值与基本回归非常接近。

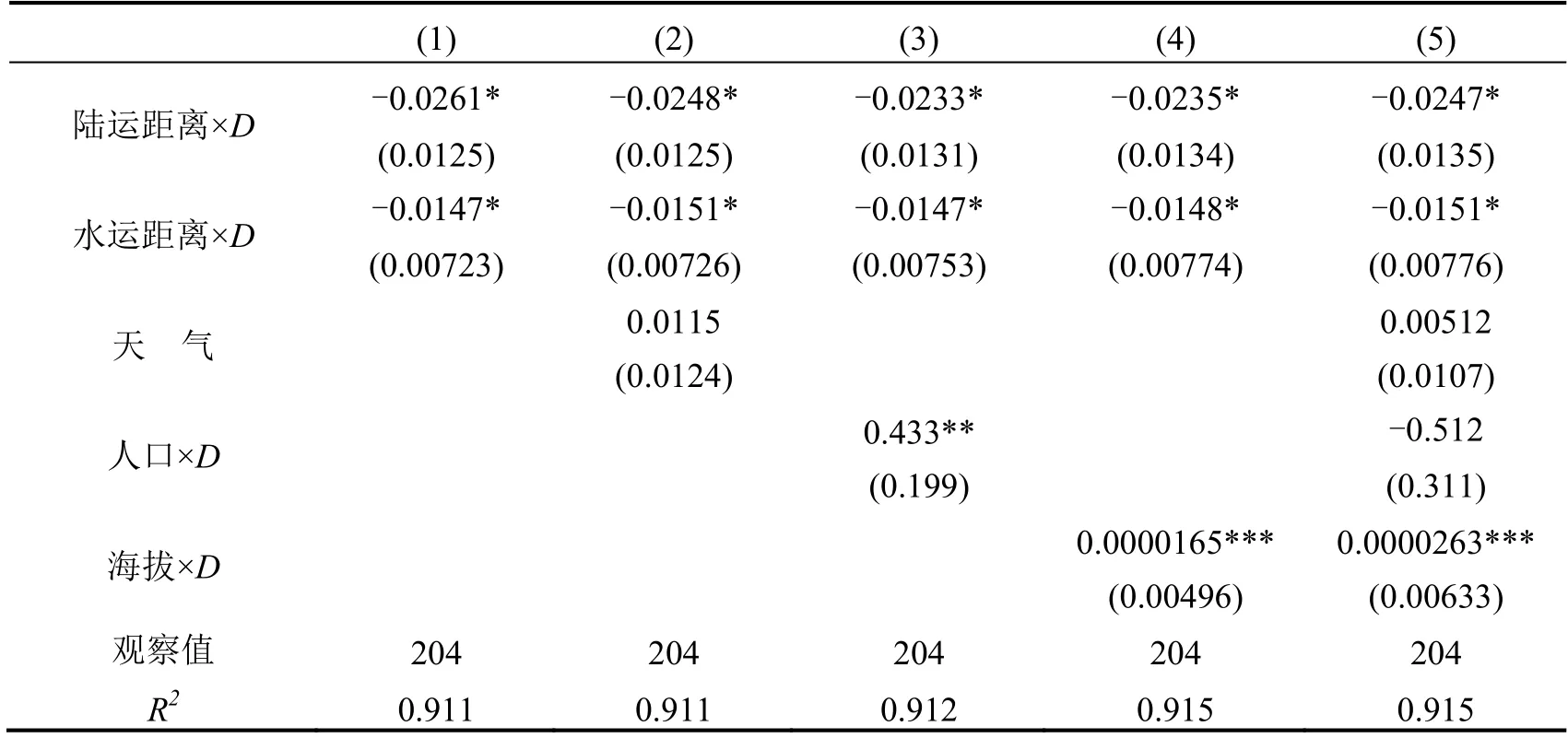
表3 增加变量的回归

2.年平均低价、高价回归

由于粮价数据中还包括每月各府的最高价和最低价，而这些最高价和最低价是来自府内各个县。因此，如果一府的高价来自与成都有较好市场联系的县，而低价则来自市场联系较差的县，那么在使用年度平均价格估计单位距离上的价格变化时，可能不能很好地反映这场外生冲击带来的影响。因此，我们分别对各府每年12个月的低价和高价作算术平均，以年平均低价和年平均高价作为被解释变量进行回归，结果如表4第一、二列所示。

第一、二列中陆运距离×D和水运距离×D的系数基本都是显著的负数，但其中第一列水运距离×D的系数不显著，这反映了商人的套利行为对低价并不是非常敏感。值得注意的是，低价的回归所得系数绝对值总体上比高价的回归所得系数值要小。这意味着与最高粮价相比，最低粮价随着各府至成都的距离增加其价格变化相对较小。这或许是由于每个府出现最低价的县相对于成都的距离较远，而出现最高价的县至成都的距离较近，并且我们采用的是府治至成都的距离，所以这是符合预期的。这进一步增强了本文结果的稳健性。

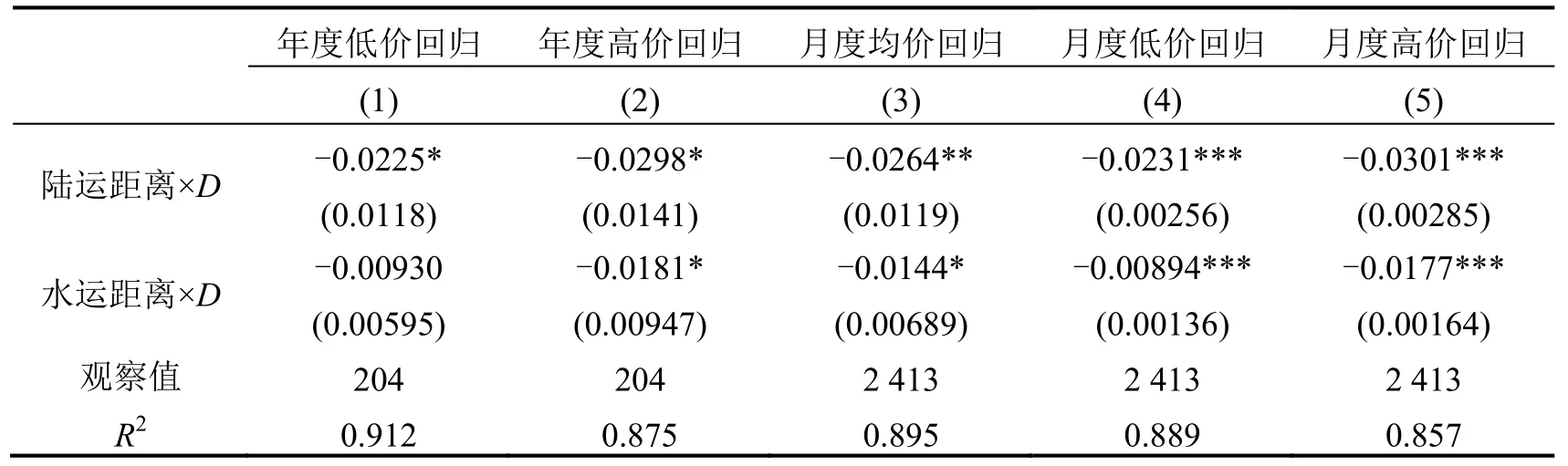
表4月度数据回归

3.月度价格回归

由于本文基本回归采用年度数据，观察值数量可能相对较少，而清代的粮价奏报制度提供了丰富的月度粮价数据，故本文也使用月度价格作为因变量进行回归。此外，为进一步消除最高价与最低价回归结果带来的偏差，本文分别作了月度均价数据、月度低价数据与月度高价数据的回归，其结果如表4第三至第五列所示，也与基本回归一致，其回归系数大小和显著性与表2估计结果没有太大差异。①除了这些稳健性检验外，本文还考察了四川省之外的情况。我们发现与四川相邻的地区几乎没有受到第二次金川之役的影响。这表明只选择四川省作为样本是合理的。这部分内容因篇幅限制未列出。

五、粮食市场整合的再讨论

前文估计的结果表明，在四川地区，陆路每百公里交通成本占粮价的2.61%左右，每百公里水运的交通成本占粮价的1.47%，陆路成本与水路成本之比为1.78。我们通过多种检验表明该估计结果的稳健性。然而，我们这里的估计毕竟是基于四川的地形和水势，这一结果是否在全国具有代表性因而可用于讨论全国各地的市场整合呢？

首先，就陆路和水路成本各自占粮价的比例而言，两者的比例可能会偏低。这有以下几方面的原因：第一，四川盆地内部平坦的地形既有利于陆路运输又有利于水路运输；二是四川盆地内部河流相对密集，特别是盆地西部的都江堰使其下游地区变得相对容易通航；三是由于粮食运输存在规模经济（彭凯翔，2015），即随着运量增加平均成本下降，而第二次金川之役恰好使当地的粮食运量较正常时期更大。②此处感谢匿名审稿人的建议。

其次，本文得到的陆路与水路成本之比与使用史料估计的结果也存在一定差异。如Evans（1984）基于史料认为该比例约为11∶1，彭凯翔（2006）也有类似的发现。我们认为这种差异来自于两种估计方法的细微差别。上述研究者使用史料进行估计，所得到的成本是与交通运输直接相关的一些成本，如付给运输工人的工资、不同交通工具（船只、马、牛等）的租金。本文采用粮价差来间接推断市场整合情况，得到的交通成本不仅包含了上述成本，还囊括了制度成本、时间成本和风险因素等。因此上述两类估计方法得到的交通成本实际上是存在一定区别的。一般来说，由于直接估计没有考虑物价因素，基于史料的估计会偏高（Evans，1984），因此这种差异是符合预期的。

如此看来，本文估算的陆路成本与水路成本之比（1.78）是比较合理的，与已有的1.5—5倍（Evans，1984）相一致。但鉴于两种成本占粮价的比例存在偏低的可能，接下来我们谨慎地将上述结论用于讨论与陆路和水路成本相联系的市场整合范围。

不同于长期的稳定的粮食贸易（如沿长江的贸易），旱涝灾害与本文所利用的自然实验类似，都是难以预测的外生冲击。因此，我们可以将前文的估计结果用于估计旱涝灾害发生时，市场整合或者粮食流动的范围。据Jia（2014）的研究，旱涝灾害会引起粮价上涨大约3%—10%。①Jia（2014）使用了与本文相同的旱涝数据和粮价数据，发现5级天气使每年8月的月度最高价上升10%左右。本文选择Jia（2014）的结论是基于以下原因：首先，《中国近五百年旱涝分布图集》提供的旱涝数据以春、夏、秋三季的情况为主，特别是夏季（陆用森，1986），并且Jia（2014）使用的粮价是每年8月的价格而非年度价格，这使得灾害发生时间与粮价变化时间比较一致，这种一致较好地避免了外地粮食输入的影响。其次，10%的结论是Jia（2014）使用月度最高价进行估计的结果。而月度中最高价能够较好地反映在没有外来粮食输入情况下的价格。总的来说，Jia（2014）的估计可以较好地反映没有外地粮食输入时的灾害冲击。以本文估计的陆路每百公里交通成本占粮价的2.61%计，在水运不发达的平原地区，比如华北，旱涝灾害最多可以导致距离冲击中心380多公里的区域内出现粮食流动。每百公里水运的交通成本大致为粮价的1.47%，在水运发达的平原地区，比如长江中下游，旱涝灾害的影响最多可以扩散至距离冲击中心大约680公里的区域。也就是说，旱涝灾害引起的市场整合的范围，是沿陆路距离冲击中心380公里和沿水路距离冲击中心680公里以内的地区。此外，由于本文对水路和陆路成本的估计可能相对偏低，这里对灾害冲击影响范围的估计，可能更适用于地形相对平坦的地区，如长江中下游和华北。对于一些山区，如云贵等地，其水路和陆路成本应该高于本文的估计，因而这些地区灾害的影响范围应当低于本文的估计。或者说，本文对灾害影响范围的估计接近实际范围的上限。

我们的估计结果均小于Shiue（2002）的估计：她发现水运不发达地区的贸易联系只限于800公里以内，水运较发达地区的贸易联系可达1 100公里。其估计结果受到了一些共同冲击的干扰，贸易联系不是唯一的影响价格的因素，也可能是两个贸易联系不太紧密的区域因与第三方区域在价格序列上表现得高度相关，从而造成市场整合程度的高估。本文的估计结果支持了施坚雅（2000）的区域市场理论，他将中国分为八个大区（除东北外）：华北、长江上游、长江中游、长江下游、东南沿海、岭南、云贵与西北，并认为区域内贸易联系比较紧密，区域之间贸易联系松散，各区之间仅中心城市存在贸易联系。本文认为，旱涝灾害的影响大致在冲击中心380公里的陆路范围和680公里的水路范围内，两个冲击范围基本上都属于施坚雅所划分的区域市场的范畴。该结果印证了Evans（1984）的观点，交通成本的限制使得前现代社会跨越几百公里运输食物至面临饥荒的邻省都是不可能的，尤其是在内陆地区。

六、结论

第二次金川之役的冲击导致成都成为粮价上涨的中心，并由此带动了整个四川省各府粮价上涨，出现了各府到成都的距离与价格差成比例的现象。本文借助此次自然实验，采用双重差分法估计了陆路和水路的交通成本。我们发现，在四川地区，每百公里陆路交通成本占粮价的2.61%左右，每百公里水运的交通成本大致为粮价的1.47%。我们通过多种检验证实了该估计结果具有稳健性。陆路成本与水路成本之比为1.78∶1，与已有的1.5—5倍之间（Evans，1984）相一致。我们进一步利用从这次自然实验中得到的交通成本，估计旱涝灾害发生时市场整合的范围。我们发现，旱涝灾害通常会导致距离冲击中心380公里的陆路范围和680公里的水路范围内的粮食流动。这个估计结果支持了施坚雅（2000）的区域市场理论。粮食市场面临外生冲击时，其影响范围通常局限在这个区域市场之内。

本文对清代交通成本的尝试性估计，为我们对清代的市场整合的理解提供了另一种视角。从研究结果我们可以发现，在交通组织和技术没有改进的情况下，清代的市场范围始终受到高额交通成本的限制。虽然清代前期的交通成本与西方相近，但是随着西方交通组织的改进和交通技术的革命，西方的市场整合程度在不断提高（Chilosi等，2013)。这种变化在一定程度上能够解释中西差距进一步扩大的原因，也在一定程度上说明了为什么在东方实现了（或近似实现了）工业化的两个国家是日本和印度（Evans，1984）。这表明关于交通以及交通成本历史的研究对于理解经济发展具有重要的意义。