基于概率语义信息公理的顾客满意度测评

耿秀丽，薄振一，张永政

(上海理工大学 管理学院，上海 200093)

0 引言

在经济快速增长的时代，为积极应对市场竞争，制造型企业更加注重顾客需求，并开始向服务型制造业转型。提高顾客满意度是现代制造型企业生存和发展的关键,企业进行合理的顾客满意度测评，有利于科学全面地了解顾客对企业的满意程度，找到满意度较低的顾客需求并有针对性地进行改进。

国外顾客满意度的研究主要集中在顾客满意度的定义、影响因素、指标体系建立和模型构建等方面。国内顾客满意度的研究最初偏重于顾客满意度与相关概念之间的关系、顾客满意度对企业的意义等理论研究。随后，更多学者将顾客满意度的理论与相关企业实证结合起来，开始转向多种类型企业的顾客满意度测评研究。文献[1]将层次分析法与模糊综合评价法结合，对申通快递的服务进行了顾客满意度测评；文献[2]应用层次分析法对第三方物流服务顾客满意度进行评价；文献[3]基于模糊网络分析法对航空公司顾客满意度进行了量化评价。以上研究通常使用网络分析法、层次分析法和德尔菲法等方法来测评顾客满意度，这些方法的优点是操作简便，但评价信息大多都是决策者主观给出，评价结果主观性强且难以保证评判信息的一致性。信息公理是公理设计中的一个重要公理，认为所有方案中，信息量最小的方案为最优方案。本文将信息公理应用于顾客满意度测评，认为所有测评指标中，信息量最小的指标顾客满意度最高。该方法利用指标的实际表现值作为评价信息，可以较为客观地评估顾客满意度，避免了人为主观因素的影响。

在信息公理中，信息量通过指标的系统范围满足设计范围的概率来表示，其中指标的设计范围是指标满足顾客期望值的分布范围，系统范围是指标实际表现的分布范围。服务型制造企业进行顾客满意度测评时，其测评指标通常包含定量指标和定性指标;针对定量指标，可以根据传统信息公理计算其信息量，通过比较信息量大小得到顾客满意度的排序[4]。针对定性指标，往往采用“差”、“中等”、“好”等模糊语言进行评估，如文献[5-6]在信息公理基础上引入了模糊集合理论，构建了定性指标模糊语言评价下信息量的计算方法。

为将信息公理应用于模糊环境中，文献[7]和文献[8]分别使用三角模糊数和直觉模糊数来处理定性指标的评价信息，这些处理方式虽然可以体现信息的模糊性，但实际情况是决策者难以用一个语义术语来表达自己的偏好，可能会在多个语义术语间犹豫不决。考虑到这一点，文献[9]基于犹豫模糊集和语义术语集提出了犹豫模糊语义术语集(Hesitant Fuzzy Linguistic Term Set, HFLTS)，它允许决策者给出多个语义术语，但是没有考虑专家对语义术语的不同偏好。针对犹豫模糊语义术语集使用中存在的问题，学者们已经开展了许多研究。Wu等[10]提出了可能性分布—犹豫模糊语义集(Possibility Distribution-HFLTS, PD-HFLTS),包含了专家对多个语义术语的犹豫信息与偏好信息，其中语义的可能性分布是均匀分布，在此基础上提出了相关的集成算子;Chen等[11]基于语义术语的相似性度量，考虑专家的态度提出了一种新的计算犹豫模糊语义可能性分布的方法;Chen等[12]提出一种评估语义分布情况的特殊方法——比例犹豫模糊语言术语集(Proportional HFLTS, PHFLTS),它是犹豫模糊语言术语集的一种拓展，其中包括每个语义术语的比例信息;Pang等[13]在犹豫模糊语言术语集的基础上提出了概率语义术语集的概念，能够表达语义的不完全概率分布信息。本文采用文献[13]中的概率语义术语集作为信息输入的表达方式，在这种输入方式下决策者针对指标的表现情况给出偏好的语义术语及其概率。概率语义术语集已经被广泛应用于多领域的评价方法中，文献[14]应用概率语义术语集开发了一种改进的质量功能展开(Quality Function Depolyment, QFD)方法，来解决创新产品设计选择问题；文献[15]将概率语义术语集应用到医院评价的多属性决策问题中；文献[16]将概率语义术语集与多准则妥协解排序(Vlsekfriterijumska Optimizacija I Kompromisno Resenje, VIKOR)方法结合，对城市的智能交通系统进行评估。本文将概率语义术语集应用于处理定性指标的评价信息，设计范围采用犹豫模糊语义术语集获取；系统范围采用犹豫模糊语义术语集和概率语义术语集获取。

本文以市场调研得到的顾客需求项作为顾客满意度测评指标，提出了基于概率语义信息公理的顾客满意度测评方法。针对定量测评指标，采用传统信息公理计算其信息量；针对定性测评指标，采用概率语义术语集和犹豫模糊语义术语集获取指标的系统范围与设计范围。考虑到两种语义信息无法直接利用信息公理公式计算，采用粗糙数方法将概率语义信息和犹豫模糊语义信息转化为区间数，然后利用信息公理计算其信息量。最后以测评指标的信息量大小为依据，对顾客满意度测评指标进行排序。以某企业客梯的顾客满意度测评为例，验证了所提方法的有效性。

1 研究框架

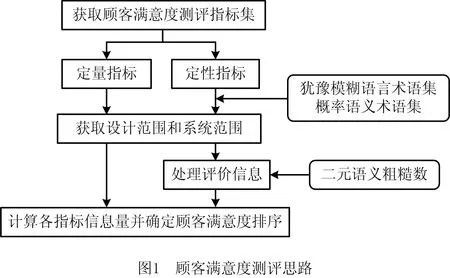
本文将概率语义术语集引入信息公理，以顾客需求作为顾客满意度测评指标，计算各指标的信息量。指标信息量越小则顾客满意度越高，从而得到测评指标的顾客满意度排序。本文所提基于概率语义术语集信息公理的顾客满意度测评思路如图1所示，具体步骤如下：

(1)通过市场调研获取相关专家和顾客的意见，确定顾客满意度测评指标。

(2)获取定性、定量指标的设计范围和系统范围。其中，定量指标的信息以区间数的形式给出;定性指标的信息以概率语义术语集和犹豫模糊语义术语集的形式给出。

(3)处理定性测评指标的模糊信息。首先，采用二元语义对概率语义信息和犹豫模糊语义信息进行预处理；然后，采用粗糙数方法将预处理后的信息转化成区间数形式。

(4)计算测评指标的信息量并排序。根据上述步骤中得到的区间数形式评价信息，采用信息量公式计算不同类型指标的信息量大小，信息量越小的指标顾客满意度最高，从而得出测评指标的顾客满意度排序。

2 相关定义

2.1 犹豫模糊语义术语集

设S={s1,s2,…,s2t+1}是一个由奇数个语义术语组成的集合，每个si代表一个不同的语义术语，如果集合S满足下列特征[17]：

(1)有序性：si>sj当i>j；

(2)存在逆运算：si=neg(sj)，i+j=2t；

(3)如果si>sj，则max(si，sj)=si，min(si，sj)=sj。

则集合S称为语义术语集。

2.2 概率语义术语集

为解决决策者在多个语义术语间犹豫不定，且对不同语义术语存在偏好的问题，文献[14]拓展了犹豫模糊语义术语集，提出了概率语义术语集的概念。

定义2[13]设S={s1,s2,…,s2t+1}是一个语义术语集，则称

L(p)={sθ(i)(pθ(i))|sθ(i)∈S,

(1)

为一个概率语义术语集。式中：sθ(i)(pθ(i))表示语义术语sθ(i)和它的概率为pθ(i);|L(p)|表示集合L(p)中语义术语的个数。

3 基于信息公理的顾客满意度测评

顾客满意度测评指标包含定量指标和定性指标。其中，定量指标使用传统信息公理计算其信息量；对于定性指标，要先将概率语义信息转化为区间数，然后利用信息公理公式计算其信息量。

信息公理认为所有顾客满意度指标中，信息量最小的指标顾客满意度最高，信息量I由成功概率来确定。设成功概率为p，则信息量为[18]：

I=-log2p。

(2)

式中p的取值由设计范围和系统范围确定。设计范围是指标满足顾客期望的分布范围，系统范围是指标实际表现的确切分布范围，系统范围和设计范围的交集称为公共范围。因此，信息量I也可以表示为

(3)

3.1 定量指标信息量计算方法

定量指标的设计范围和系统范围通常以某一区间范围的形式给出，例如某机械产品噪音大小的设计范围为45～55 dB，系统范围为50～60 dB。这类指标可直接利用式(3)求解。

但有些定量指标的系统范围具有随机性，例如某项服务的等待时间服从正态分布。此类定量指标的信息量很难直接求解，文献[19]针对此问题提出了一种信息量积分算法：

(4)

式中：f(Ci)为指标Ci的系统范围的概率密度函数;drl和dru为设计范围的上界和下界。

3.2 定性指标信息量计算方法

针对定性指标，例如某产品的服务质量、安全性和节能性等指标，往往采用“好”、“一般”和“差”等模糊语言表达其表现情况。为解决指标的表现值可能在不同语义术语间犹豫不定的问题，本文采用概率语义术语集描述顾客满意度测评定性指标的表现情况，采用其获取定性指标的设计范围和系统范围，进而利用信息公理公式计算信息量。

为计算定性测评指标的信息量，本文需要将概率语义信息转换为区间数。首先采用二元语义对信息进行预处理，然后采用粗糙数方法将预处理后的信息转换为区间数。二元语义的计算过程简便，其运算后的结果往往能与事先定义的语义信息相对应，是一种有效的词计算方法。

定义3[20]设S={s1,s2,…,s2t+1}是一个语义术语集，对于其中任一语义术语si，其相应的二元语义可通过转换函数φ得到：

(5)

定义4[20]β∈[0，2t+1]为语义术语集S运算的结果，令i=round(β),i∈[0,2t+1]。与β相应的二元语义可由函数Δ得到：

Δ[0，2t+1]→S×[0.5,-0.5)，

(6)

(7)

其中：round为“四舍五入”取整算子，α为符号转移值。

反之，令(si,αi)为一个二元语义信息，则一个逆函数Δ-1可将该信息转换为相应的数值β∈[0，2t+1]，即

Δ-1：S×[0.5,-0.5)→[0,2t+1]，

(8)

Δ-1(si,αi)=i+αi=β。

(9)

例如，L1(p)={s2(0.7),s3(0.3)}，L2(p)={s3(0.3),s4(0.4),s5(0.3)}为两个概率语义术语集，根据二元语义处理方法可以将其处理为Δ-1(L1(p))={2(0.7)，3(0.3)}，Δ-1(L2(p))={3(0.3)，4(0.4)，5(0.3)}。

采用二元语义方法处理概率语义信息之后，再采用粗糙集方法将其转换为区间数。粗糙集是一种新的数学工具，采用目标集合的下近似和上近似来表达和处理模糊信息。粗糙数方法采用区间数的形式表达信息的不确定性，利用需要处理的数据信息来确定区间的上下限，其过程不需要先验信息，保证了信息的客观性[21]。

假设U是所有信息中所有对象组成的论域，所有对象可以分为n个类，组成集合R，R={C1,C2,…,Cn}。设n个类的排序为C1

(10)

Ci的上近似域定义为：

(11)

Ci的边界域定义为：

Bnd(Ci)=∪{Y∈U|R(Y)≠Ci〉={Y∈U|

R(Y)>Ci〉∪{Y∈U|R(Y)

(12)

(13)

(14)

式中ML和MU分别为Ci下近似域和上近似域中对象的数量。

采用粗糙数的概念将Ci表示为Rnum(Ci)，则

(15)

(16)

(17)

Δ-1(L1(p))={[2,3.4],[2.67,3.75]}

=[1.101,1.753]，

Δ-1(L2(p))=[1.007,1.475]。

同理，可将犹豫模糊语义信息转换为区间数。将定性指标的设计范围和系统范围同时转换为区间数后，利用式(3)计算定性指标的信息量。

4 案例分析

4.1 案例应用

某企业是一家电梯制造商，主要生产客梯、货梯和医用电梯等电梯产品。为了增强自身竞争能力，该公司开始重视提升顾客满意度，以满足顾客不断增长的需求。本文将所提方法用于该公司的客梯顾客满意度测评中，通过问卷调查和顾客/专家访谈等市场调研方法获取的顾客满意度测评指标包括：舒适性(C1)、安全可靠性(C2)、噪音大小(C3)、平均等待时长(C4)、维修技术水平(C5)、节能程度(C6)、保养频率(C7)、维修成本(C8)、服务效率(C9)。其中，C1～C4为定量指标，舒适性(C1)通过电梯运行加速度体现，安全可靠性(C2)通过每五万次运行出现故障的次数体现；C5～C9为定性指标，通过调研，指标C5～C7的系统范围在语义间的可能性分布相同，采用犹豫模糊语义术语集评价，指标C8和C9的系统范围在语义间的可能性分布不同，采用概率语义术语集评价。对于定性指标的评价，采用7粒度的语义术语集合，即S={s1：非常差，s2：很差，s3：差，s4：一般，s5：好，s6：很好，s7：非常好}。

步骤1通过调研指标的期望表现情况和实际表现情况，得出指标的设计范围和系统范围，如表1所示。

表1 顾客满意度测评指标及其设计范围和系统范围

步骤2根据式(5)～式(17)，将定性指标的设计范围和系统范围转化成区间数形式。结果如表2所示。

表2 定性指标信息转化结果

步骤3根据式(3)，计算每个指标CRi的信息量Ii，结果如表3所示。

表3 各指标的信息量

由表3可得顾客满意度测评的结果为：C9>C6>C1>C7>C4>C8>C2>C5>C3，表示服务效率(C9)的顾客满意度最高，噪音大小(C3)的顾客满意度最低。

4.2 对比分析

为了验证所提方法的有效性，本文利用文献[6]所提的三角模糊信息公理方法与本文所提方法进行对比，其信息公理的求解公式为

C1～C5为定量指标，计算方法与本文方法相同。对于定性指标C6～C9，根据文献[6]中语义与三角模糊数的对应转换关系，将案例中犹豫模糊形式语言信息分别转化成对应三角模糊数并进行加权处理。文献[6]中三角模糊数与语义对应关系如下：s1(0,0,0)，s2(0,0.1,0.2)，s3(0.1,0.3,0.5)，s4(0.3,0.5,0.7)，s5(0.5,0.7,0.9)，s6(0.8,0.9,1)，s7(1,1,1)，则指标C6～C9的设计范围和系统范围转化结果如表4所示，信息量计算结果如表5所示。

表4 三角模糊数转化结果

表5 三角模糊信息公理计算所得各指标信息量

由信息量可知顾客满意度排序为C8>C9>C1>C4>C7>C6>C2>C5>C3。文献[6]方法计算出的顾客满意度排序与本文方法的结果相比，相同点是服务效率(C9)的顾客满意度仍较高，排在第2位；噪音大小(C3)的顾客满意度仍最低，说明了本文方法的有效性。不同点在于4个定性指标的满意度排序发生了较大变化。这是因为在使用三角模糊数进行描述时，只能选择一个三角模糊数作为描述信息，在进行加权运算时可能会造成信息的不准确和丢失，而本文所提的概率语义信息公理方法，既允许同时选择多个语义变量，又能够体现不同语义的可能性分布，更具客观性和准确性，也更加符合真实的测评环境。

5 结束语

提升顾客满意度是制造型企业增强竞争能力的重要途径，顾客满意度测评是提升顾客满意度的重要前提。本文将概率语义术语集和信息公理相结合，通过计算顾客满意度测评指标的信息量反映顾客满意程度大小，对测评指标进行满意度排序。所提方法的特点如下：

(1)将信息公理引入顾客满意度测评中，该方法基于指标的客观表现值对满意度进行测评，解决了以往顾客满意度测评中评价信息过于主观的问题，同时也避免了决策者给出指标权重的主观过程。

(2)将概率语义术语集与信息公理结合，充分避免了信息的损失，比较全面地反映了所研究对象的实际表现情况，得出的顾客满意度排序也更加真实。

通过对某企业客梯顾客满意度测评的研究分析，表明了所提方法的有效性与可行性，但也存在一些不足，下一步将考虑指标间的影响关系产生的补偿效应对满意度测评结果的影响。本文采用了一类概率语义术语集的定义，其相关概念在供应链管理、应急管理等基础研究领域都有广阔的研究空间。虽然概率语义术语集的概念与表达方式缺乏严谨性，但是这个概念的应用不会影响数学逻辑上的正确性，因此文中暂且使用概率语义术语集，后续将展开更深入的研究。