基于混合选择的多目标进化算法及其在优化设计问题中的应用
2020-08-21王万良李伟琨臧泽林赵燕伟
王万良,李伟琨,臧泽林,赵燕伟,2
(1.浙江工业大学 计算机视觉研究所,浙江 杭州 310023;2.浙江工业大学 特种设备制造与先进加工技术教育部/浙江省重点实验室,浙江 杭州 310014)
0 引言
随着时代的发展,研究不断深入,传统以人工干预为主、依靠经验进行工程设计优化的方式已很难满足现行优化设计的需求。此外,随着用户需求的提升,设计元素更加多元化,工程设计优化问题也由传统的单一目标优化问题转换为复杂的多目标优化问题。因此,许多新的技术被用来解决工程设计优化问题,其中进化算法扮演了重要的角色。随着遗传算法(Genetic Algorithm, GA)[1]的提出,新的进化算法不断涌现,如差分进化算法(Differential Evolution, DE)[2]、进化策略(Evolutionary Strategy, ES)[3]、粒子群优化算法(Particle Swarm Optimization, PSO)[4]、进化规则(Evolutionary Programming, EP[5]、蚁群优化(Ant Colony Optimization, ACO)算法[6]等。尽管如此,在解决实际工程优化设计问题时,仍会面临许多挑战如复杂约束[7]、不确定性[8]、局部最优[9]等。在这其中,多目标工程优化设计问题由于无法像单目标优化问题那样找到一个单独的最优解来满足所有的优化目标[10],逐渐成为了研究的热点。区别于早期的单目标工程设计最优化问题,多目标优化问题最终得到的解往往是一组相互冲突目标间权衡取舍后的结果集合[11],它们被称为帕累托最优解集(Pareto optimal set)或非支配解集(non-dominated set)[12]。针对此类问题,已有学者提出了可行的算法,这些算法主要归纳为以下几大类:
(1)基于群智能的进化算法 这类算法往往脱胎于生物的群体行为,如多目标粒子群优化(Multi-Objective Particle Swarm Optimization, MOPSO)算法[13]、多目标人工蜂群(Multi-Objective Artificial Bee Colony, MOABC)算法[14]、多目标漩涡搜索算法(Multi-Objective Vortex Search Algorithm, MOVSA)[15],多目标细菌觅食优化算法(Multi-Objective Bacteria Foraging Optimization Algorithm, MOBFOA)[16]、混合多目标萤火虫算法(Hybrid Multi-Objective Firefly Algorithm, HMOFA)[17]、改进蚁群算法(Improved Ant Colony Algorithm, IACA)[18]、改进的多目标布谷鸟算法[19]、改进的多目标蜂群算法[20]等。但该类算法的性能往往也受限于其生物群体行为准则。
(2)基于松散支配的进化算法 该类算法大多提出了一种支配准则来有效筛选个体,如强化帕累托进化算法(Strength Pareto Evolutionary Algorithm,SPEA)[21]、改进的强化帕累托算法(Improving the Strength Pareto Evolutionary Algorithm,SPEA2)[22]、ε支配[23]、基于CDAS(control dominance area of solutions)支配[24]、基于α支配[25]、基于网格的进化算法(Grid-based Evolutionary Algorithm, GrEA)[26]等。但是由于该类算法往往着重于强化算法的收敛性,有时会导致算法在保持解的多样性方便造成负面的影响。
(3)基于分解的进化算法 该类算法往往通过使用一系列权重向量来生成多个聚合函数,从而将复杂的问题分解成多个子问题。如基于分解的多目标进化算法(Multi-Objective Evolutionary Algorithm based on Decomposition, MOEA/D)[27],基于分解的高维多目标进化算法(Improved Decomposition-based Evolutionary Algorithm, I-DBEA)[28],基于支配与分解的高维多目标进化算法(Multi-objective Evolutionary Optimization Algorithm based on Dominance and Decomposition, MOEA/DD)[29]等。但该类算法受限于其所使用的分解函数,在高维空间中可能会对解的多样性维护造成影响。
(4)基于评价指标的算法(indicator-based approach) 为了在目标空间中获得最优的解排序,很多学者提出了了基于评价指标的多目标算法,例如基于指标的进化算法(Indicator Based Evolutionary Algorithm, IBEA)[30]、基于超体支配的多目标进化选择算法[31]、基于超体积级的进化算法(fast Hypervolume based Evolutionary algorithm, HypE)[32]等。
(5)基于参考信息的算法(reference set based approach) 该类算法大多采用一组参考信息来辅助算法,并指导其搜索过程。如带精英策略的快速非支配排序遗传算法(fast elitist Non-dominated Sorting Genetic Algorithm, NSGA-Ⅱ)[33]、NSGA-Ⅲ[34]、参考向量引导进化算法(Reference Vector guided Evolutionary Algorithm, RVEA)[35]等进行多目标优化。尽管该类算法都可以不断向真实最优帕累托前段趋近,但大多单独使用角度或距离来对种群进行划分,这往往会遗失部分优秀的个体。此外,就像No Free Lunch理论中证明的一样,并不存在一种算法可以解决所有优化问题[36],而这也是进化计算在工程设计优化研究领域不断创新的动力所在。鉴于此,本文提出一种基于混合选择的多目标优化算法(Hybrid Selection based Multi-objective Evolutionary Algorithm, HSMEA)来解决上述问题,该算法的主要创新如下:
1)算法设计了新的个体划分方法,该方法通过综合考虑候选个体与参考向量间的距离和夹角,高效地将候选个体分为不同的簇,从而为后续优秀个体的筛选打下基础。
2)对于划分好的子种群,算法采用两种不同的机制来有效地筛选优秀个体:本文首先提出一种基于全局网格密度排序的选择机制,该机制通过构建网格坐标,在选择具有良好收敛性个体的同时,最大程度地保持其多样性。此后,算法采用基于指标的选择机制,进一步强化与巩固筛选出个体的收敛性与多样性。
1 背景简介
1.1 多目标优化问题
为了不失一般性,本节首先介绍多目标优化问题的基础概念。多目标优化问题(Multi-objective Optimization Problem, MOP)在数学上可用下式表示:
minF(x)=(f1(x),f2(x),f3(x),…,fm(x))T。
(1)
式中:x=(x1,x2,x3,…,xn)为n维向量;X为n维决策空间;目标函数F:X→m,其中m表示目标个数,m表示目标空间。此外,围绕多目标优化问题产生的帕累托最优相关概念最初由Edge和Pareto提出[37],其具体定义如下[38]:
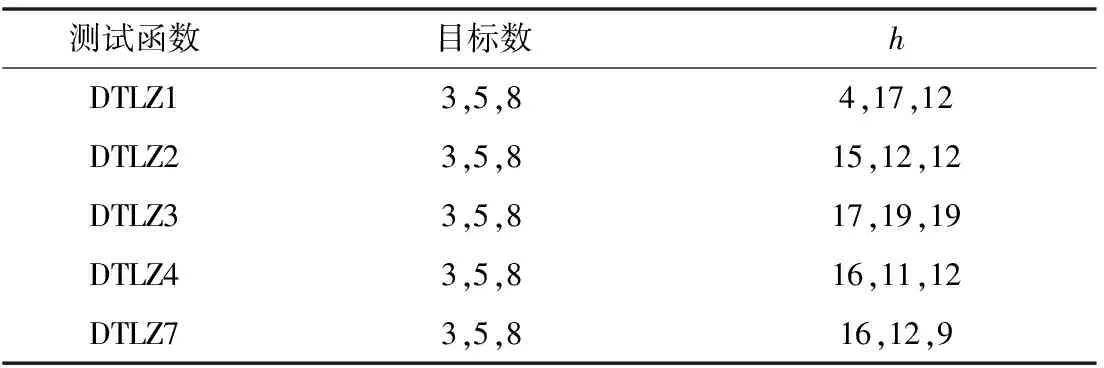
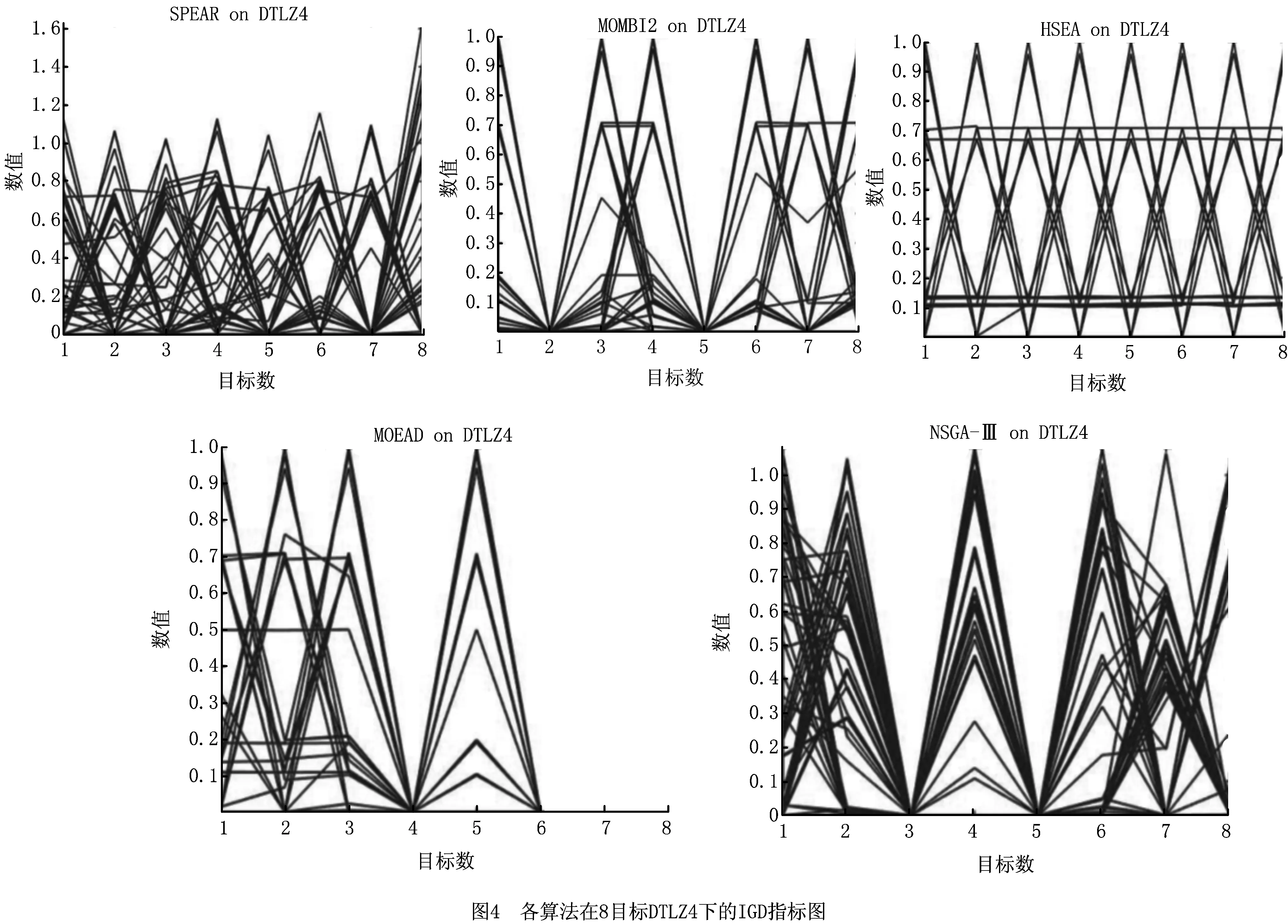
定义1帕累托占优/支配。给定两个向量x,y∈X,其对应的目标向量为f(x),f(y)。称x支配y(记作xy),当且仅当∀i∈(1,2,…,m),fi(x)≤fi(y)且满足∃j∈(1,2,…,m),fj(x) 定义2帕累托最优解。给定一个决策向量x∈X,称其为帕累托最优解(也称为非支配解),当且仅当y∈X,使得yx。 定义3帕累托最优解集。所有帕累托最优解(PS)的集合称为帕累托最优解集(也称为非支配解集),PS={x∈X|y∈X,yx}。 定义4帕累托最优前端。所有帕累托最优解所组成的图像即为帕累托最优前端,其数学表达式如下:PF={F(x)|x∈PS}。 定义5理想点。给定一个向量g=(g1,g2,…,gm),则g被称为理想点,如果满足g是fi(x)下确界,其中i∈(1,2,…,m)。 定义6最差点。给定一个向量g=(g1,g2,…,gm),则g被称为最差点,如果满足g是fi(x)的上确界,其中i∈(1,2,…,m) HSMEA采用参考向量机制来辅助算法完成优秀个体的筛选。作为整个算法的基本机制,HSMEA使用的所有参考向量均为第一象限内的单位向量,起始点是初始点。理论上,这种单位向量可以通过任意向量除以其范数生成。但在实践中,为了生成均匀分布的参考向量,本文采用文献[34]中的方法,首先使用规范的设计方法生成单位超平面上的一组均匀分布点,如图1所示;其次将点放在归一化的超平面上,参考点的数量N取决于客观空间的目标数M和正整数H的维数,定义为 (2) 参考向量是本文所提HSMEA的基本机制。一方面,在HSMEA中采用候选解与参考向量之间的锐角和垂直距离来进行筛选;另一方面,HSMEA倾向于发现接近帕累托最优前端,且与参考向量相本文通过参考向量的辅助来实现后续解的筛选操作。 HSMEA采用流行进化算法的设计框架,整体由4个主要阶段组成。在初始化阶段,初始个体和参考向量被随机初始化;随后,通过应用交叉和变异操作获得一组子代解决方案;最后,通过在混合选择步骤中先完成子集的划分,再采用两种不同的机制筛选出优秀个体生成解决方案P。下面详细解释HSMEA中各个环节。 算法1HSMEA算法。 1. Output:Final population P 2. Initialization:initial population P0, reference Vector V, 3. While(t 4. pt←Mating-Selection(P0) 5. Q←Variation(pt) 6. S←pt∪Q 7. Pt+1←Hybrid-Selection(t,S,V) 8. t=t+1 return P 在初始化阶段,算法首先生成初始种群和参考向量。具体而言,从决策(变量)空间随机抽样生成初始父群体P0,并通过1.2节阐述的参考向量构建方法生成一组参考矢量V=(V0,V1,…,Vn)。 随后在HSMEA中,进行交叉操作与变异操作,从而产生新的候选解决方案。在这里采用多项式变异和模拟二进制交叉(Simulated Binary Crossover, SBX)[32]来完成对个体的交叉与变异操作。 在混合操作中,算法首先提出一种新的子集划分策略,并通过参考向量的协助将个体划分为N个子集。随后,针对每个子集,算法采用基于网格密度策略和基于指标策略混合筛选优秀的个体。 2.2.1 子集划分 本算法采用的参考向量初始点为坐标原点,因此在对种群进行划分前首先对目标值进行标准化处理,使其与参考向量相匹配,具体步骤如下: (1)给定种群S中个体的目标Ft={ft,1,ft,2,…,ft,|pt|},其中t为当前代数,则标准化处理后的目标值 (2) (3) (4) (3)根据θt,i,j与dp的值来定义不同个体的归属。当前大多数算法在划分子种群时,往往只单独考虑角度或者距离,这导致在划分子种群时出现部分信息的缺失与不准确。本文提出一种新的划分策略,综合考虑了角度与距离,使得划分更加合理与准确,其具体定义如下: 给定种群中的任一个体I,它归属于子集St,k,当且仅当AD的值最小: St,k={It,i|k=argmaxADt,i,j}。 (5) 式中ADt,i,j为混合距离,ADt,i,j=dp+θt,i,j,i=1,2,…,|St|,j=1,2,…,N。 在完成上述操作后,种群中所有的个体都被划分到了相应的子种群中,接下来通过两种机制从每个子种群中混合筛选出优秀的个体。 2.2.2 网格密度筛选机制 为方便从子种群中筛选出优秀个体来构成新的种群,本文提出一种基于网格密度的筛选机制来辅助算法对多样性较好的个体进行优先筛选,从而强化解集的多样性。网格机制通过将分布密度不同的个体划分在不同的网格内,并通过构建其网格坐标等来高效地对个体进行评价[26]。为方便构建网格坐标,本文首先引入m个目标下的网格机制上下界: (6) (7) 其中:maxfm(x)、minfm(x)分别表示第m个目标下的最大值和最小值;h为固定常数,h≥2。因此,第m目标下个体的坐标可表示为 (8) GDR(x)=find(GD(x,y) (9) 如图3所示为双目标问题(m=2),个体p1,p2,p3,p4,p5的网格坐标分别为(1,5),(2,5),(2,4),(2,3),(1,3)。对于个体p1,其与p2,p3,p4的GD值分别为1,2,2,3,因此其GDR值为1;而对于个体p3,其与p1,p2,p4,p5的GD值分别为2,1,1,2,其GDR值为2。p1的GDR值更小,因此优先选择p1(从个体的多样性来看,p1相比p3其周围拥挤度较低,多样性更好)。 2.2.3 基于指标的筛选机制 为了更好地平衡最终所得解集的多样性与收敛性,在完成采用网格的筛选机制来强化解的多样性后,本文采用基于解质量指标Iε+的筛选机制[30]来进一步强化解的收敛性。该指标定义了一个个体在目标空间中支配另一个个体所需的最小距离,具体定义如下: Iε+(x,y)=min(fi(x)-ε≤fi(y))。 (10) 式中i∈(1,2,…,m),m为目标数。个体的适应值可以定义为 (11) 式中c=max|I(x,y)|。在采用基于指标的筛选过程中,F(xi)值小的个体将被优先选择,剩余的个体将会被更新,最终获得新的解集。 HSMEA的归一化和范数的计算需要增加O(mN),其中m为目标数,N为总体大小。子集划分的时间复杂度为O(mN2)。此外,算法还采用了混合选择策略来强化和巩固所得解得收敛性与多样性,其时间复杂度均为O(mN2)。综上所述,HSMEA的复杂度近似于O(mN2)。 本章将HSMEA和4个现行的多目标优化算法(SPEAR[39],MOEA/D,MOMBI2[40],NSGA-Ⅲ)在DTLZ1,DTLZ2,DTLZ3,DTLZ7标准测试函数上,针对3,5,8目标的优化问题进行对比分析,其参考向量与初始种群设定如表1所示。此外,还引入了两个标准评估指标反转世代距离(Inverted Generational Distance, IGD)[41]与超体积(HyperVolume, HV)[42]来更好地评估算法的性能。 表1 HSMEA中参考向量与初始种群的设定 对于算法所采用的SBX,其中两个参数ηc=30,ηm=20。此外,对于MOEA/D算法,其邻域大小T设定为20;MOMBI中两个参数α=0.5,ε=0.001。为保证实验客观性,以上算法参数设定均遵循其原文设定。对于HSMEA,由于采用了基于网格的机制来进行筛选,其中的参数网格划分h在不同测试函数不同目标下的设定如表2所示。 表2 HSMEA中表格划分h在各测试函数下的设定 采用IGD指标与HV指标的实验统计结果如表3~表4所示,其中灰色标识的值为该行中的最优结果。为了方便对比与分析,在实验部分引入秩序检验来评价各个算法所得结果间的差异性,其统计结果以“w/l/t”的形式被记录在各表格最后一行,其中:w表示该对比算法的结果优于本文提出的HSMEA所获得结果;l表示该对比算法所获得的结果差于本文提出的HSMEA所获得结果;t表示该对比算法的结果与本文提出的HSMEA所获得结果无明显的差异。 表3 各算法在IGD指标下的统计结果 如表3所示为5个算法在IGD指标下进行15次运算后的统计结果(中值与标准差),表中“+”表示该对比算法的结果优于HSMEA,“-”表示该对比算法的结果差于HSMEA,“=”表示该对比算法的结果与HSMEA无明显差异。由统计结果可以看出,HSMEA与NSGA-Ⅲ两个算法包揽了所有12个测试函数在IGD指标下的最优值(最小值)。对于DTLZ1测试函数,HSMEA在3,5,8三个目标上均获得了良好的表现,而对于DTLZ2测试函数,MOMBI2和SPEAR两个算法均表现良好,从秩序检验的结果来看,部分结果与HSMEA所获得结果相似,但HSMEA的计算结果仍为所有算法结果中的最优值。在DTLZ4上,MOEA/D和MOMBI2的表现较差。如图4所示为5种算法在8目标DTLZ7上的帕累托前沿图,从图中可以看出HSMEA所获得的解表现出了良好收敛性与分布性潜力。 对于DTLZ7测试函数,尽管3,5,8目标下的最优值被NSGA-Ⅲ算法所获得,但根据秩序检验结果,HSEA的结果与NSGA-Ⅲ算法的结果无明显差异。从表3数据亦可看出,HSMEA在部分目标上所获得结果明显优于MOEA/D等算法。 表4所示为5种算法在DTLZ上基于HV指标的测试结果。为了方便计算,本文采用标准化处理的HV指标,数值越大,其在HV指标上的表现越优秀。从表4可以看出,DTLZ1,DTLZ2,DTLZ3,DTLZ7测试函数在3,5,8目标上的最优值分别被HSMEA,MOMBI2和SPEAR所获得。对于DTLZ1,DTLZ2测试函数,HSMEA表现良好,获得了所有的最优值;对于DTLZ2,尽管NSGA-Ⅲ,MOMBI2,SPEAR算法在5目标下的表现良好,但在3,8目标下的表现略差于HSMEA;对于DTLZ4测试函数,HSMEA所获得结果略逊于SPEAR。尽管如此,本文提出的HSMEA在DTLZ4上仍然优于大部分算法;对于DTLZ7测试函数,HSMEA获得了3目标与8目标下的最优值,而MOMBI2获得了5目标下的最优值,NSGA-Ⅲ在5目标下的表现也非常良好,但从8目标下DTLZ7的数据可以看出,MOMBI2和NSGA-Ⅲ的表现明显不如之前,而HSMEA的结果明显优于其他4个算法。综上所述,得益于良好的子集划分策略与混合选择操作的辅助,HSMEA在解决这些多目标优化问题上具有良好的性能与潜力。 表4 各算法在HV指标下的统计结果 本节将HSMEA应用到实际的工程优化设计问题中,并与3种已实现的算法(NSGA-Ⅱ,MOALO[43],PAES[44])进行了对比分析,进而验证算法的良好性能。 3.3.1 减速器优化设计问题 减速器优化设计问题是机械工程领域中一个较为突出的优化设计问题[45],该问题主要针对减速器的重量f1与应力f2的最小化。此外,该问题包含7个设计变量:齿轮面宽度x1、齿模x2、小齿轮的齿数x3、轴承1的间距x4、轴承2的间距x5、轴1的直径x5、轴2的直径x7。其具体数学模型描述如下: (12) (13) s.t. g9:1.9-x5+1.1x7≤0, 其中:2.6≤x1≤3.6,0.7≤x2≤0.8,17≤x3≤28,7.3≤x4≤8.3,7.3≤x5≤8.3,,2.9≤x6≤3.9,5.0≤x7≤5.5。 在本节中,HSMEA与其他3种算法在减速器优化设计问题上的运行代数为1 000,每个算法单独运行15次,h设定为10,并做统计分析。此外,为了方便对实验结果进行对比分析,本节引入两个通用性指标:世代距离(Generational Distance, GD)[45]与空间指标(Spacing, SP)[46],通过这两个指标可以直观方便地评估各个算法在实际问题中所获得解得优劣程度。 如表5所示为MOPSO,NSGA-Ⅱ,MOALO和HSMEA算法在减速器优化设计问题上采用GD和SP指标的实验结果,表中数值为运行15次后的平均值与标准差,灰色标记为该指标下的最优值。 表5 各算法在减速器优化实际问题上采用GD与SP指标的统计结果,其中灰色标记部分为最优值 从表5中数据可以看出,HSMEA在GD指标和SP指标上都取得了最好的解,而算法MOPSO,NSGA-Ⅱ与MOALO在该问题上尽管表现较好,但对比本文提出的HSMEA算法仍存在劣势。 3.3.2 四杆平面桁架优化设计问题 四杆平面桁架优化设计问题是工程优化领域中较为突出的优化问题,其目标主要围绕4杆桁架的结构体积f1和位移f2的最小化展开,其具体公式如下[43]: (14) (15) s.t. 1≤x1≤3,1.414 2≤x2≤3, 1.414 2≤x3≤3,1≤x4≤3。 在该问题上,HSMEA与其他3种算法采用GD和SP指标的实验结果,运行代数为1 000,每个算法单独运行15次,其统计分析结果如表6所示,其中灰色标记部分为最优值。 表6 各算法在四杆平面桁架优化设计问题上采用GD与SP指标的统计结果 从表6中的结果可以看出,GD指标和SP指标上的最优值均被HSMEA所获得。值得注意的是,MOALO在该问题上的表现也较为突出,特别是在GD指标下,其数据的波动较小,但在SP指标下,相比本文提出的HSMEA,仍略逊一筹。 3.3.3 盘式制动器优化设计问题 盘式制动器优化设计问题最早由Ray等[47]提出,是具有复杂的混合约束问题。该问题主要围绕停止时间f1和盘式制动器的制动质量f2两个目标展开,具体包含4个设计变量:磁盘的内半径x1,磁盘的外半径x2,啮合力x3和摩擦表面的数量x4,模型公式如下: (16) (17) s.t. g1(x)=20+x1-x2,g2(x) =2.5×(x4+1)-30, 其中:55≤x1≤80;75≤x2≤110;1 000≤x3≤3 000;2≤x4≤20。在该问题上,HSMEA与其他3种算法的统计分析结果如表7所示,其中灰色标记部分为最优值。表7所示为MOPSO,NSGA-Ⅱ,MOALO和HSMEA算法在盘式制动器优化设计问题上采用GD和SP指标的实验结果。从表中数据可以看出,HSMEA包揽了在GD指标和SP指标下均值和标注差的最优值。对于MOPSO,NSGA-Ⅱ与MOALO,尽管3种算法在处理该问题的表现较为良好,但对比本文提出的HSMEA算法,仍有一些劣势。 表7 各算法在盘式制动器优化设计问题上采用GD与SP指标的统计结果 综上所述,MOPSO,NSGA-Ⅱ以及MOALO算法单纯使用进化的操作来对数据进行优选,面对复杂约束问题,其很难达到较好的效果。而本文提出的HSMEA,一方面采用参考向量来辅助算法高效运算,另一方面基于网格和基于指标两种筛选机制都进一步巩固与强化了算法解的收敛性与多样性,从而在实际问题中取得了较好的效果。 为进一步提升算法收敛性,同时最大化保留解的多样性,并有效解决实际工程中的优化设计问题,本文提出一种基于混合选择的多目标进化算法HSMEA。该算法首先利用融合角度与距离的动态聚类方法对种群进行子集划分,从而在多目标优化中更好地实现收敛和多样性之间的平衡;其次引入包含两种不同原则(基于网格和基于指标)的混合选择机制,从而进一步强化和巩固算法的收敛性和多样性。此外,本文对HSMEA和其他4种先进的进化算法进行了广泛的实验比较,并选取DTLZ测试基准问题来研究和评估算法的能力。最后,在实际的减速器优化设计问题、四杆平面桁架优化设计问题和盘式制动器优化设计问题上进行了实例验证。统计结果显示,本文提出的HSMEA在测试问题和实际优化问题上都表现出了良好的性能与潜力。但是,在本文采用的实例上表现良好,并不代表其可在所有的实例中表现良好,不同的实际问题与环境更需要针对性的选择与设计算法。未来将扩展HSMEA,通过结合约束处理技术解决高维度的约束多目标问题,以进一步验证其有效性。1.2 参考向量

2 HSMEA框架
2.1 初始化与子代生成
2.2 混合选择操作







2.3 算法复杂度分析
3 实验设计与描述

3.1 参数设定
3.2 结果分析与讨论


3.3 工程实例应用



4 结束语
