面向低压电器的CPN协同装配任务建模与优化

张立彬,吕焕培,2,胥 芳,谭大鹏+,陈教料,林 琼

(1.浙江工业大学 机械工程学院,浙江 杭州 310014;2.宁波财经学院 机械与电气工程学院,浙江 宁波 315175)

0 引言

低压电器是一种根据外界输入信息，手动或自动地接通、断开电路，以实现对电路或非电对象的切换、控制、保护、检测、变换和调节的元件或设备，其一般用于额定交流电压小于等于1 200 V或者直流电压小于等于1 500 V的电路中[1]。该类电器广泛地应用于农业、交通、国防以及民用用电部门中。但低压电器作为一种复杂装配件，其结构类型多样，生产批量多变，因此目前多采用以人工装配为主的劳动密集型装配方法。随着我国人口红利逐渐消失，用工成本逐年提高，这种装配模式已不能满足企业的市场竞争的需要。因此,构建一种适用于低压电器装配的协同、高效的自动化装配方法显得尤为必要。

根据产品的装配特点来构建相应的装配方法，并进行平衡优化，是产品装配控制所要研究的主要问题之一。余梦雨等[2]针对多批量小品种产品的装配特点，提出一种柔性装配系统的设计方法，实现了装配任务的现场实时调整；Shao等[3]提出一种基于模块化设计及优化的智能柔性装配方法，对多种类、变批次的产品进行装配；Nourmohammadi等[4]提出一种实现多目标装配的U型装配系统，并引入帝国竞争算法对装配平衡进行优化来提高系统的装配效率;Chou等[5]就液晶显示器(Liquid Crystal Display, LCD)装配，提出了多目标混合遗传算法(Multi-objective Hybrid Genetic Algorithm, MO-HGA)，使得在TFT-LCD(thin-film transistor-liquid crystal display)液晶屏晶体单元的装配过程中，可以同时装配不同用户所要求的LCD屏幕;Çil等[6]通过引入束搜索的方法对机器人平行装配系统进行构建和优化;侯伟伟等[7]引入粗粒度的装配任务和细粒度的装配操作，基于装配任务和装配操作，建立了一个基于层次链的装配方法;郑时雄等[8]采用基于并行思想的约束网络方法对机器人柔性装配系统进行建模，并应用遗传算法对装配进行平衡优化;李明富等[9]就多种混合产品装配的平衡优化问题，提出一种改进性的IWD(intelligent water drop)算法来提高装配效率;Li等[10]提出一种重置模拟退火算法对双侧装配线进行了装配优化，实现产品装配过程中的装配周期最短化;Ponnambalam等[11]以装配系统中的装配单元数、装配效率及装配平滑指数为优化参数，提出一种多目标遗传算法，对整个装配系统进行装配平衡优化。这些研究内容为面向低压电器的装配方法构建及其平衡优化提供了有力的支持。由于低压电器具有种类繁多、型号各异及生产批量多变的特点，对其进行协同装配存在一定的困难，同时在装配过程中，各装配单元间的无序竞争及交互的不平衡性，影响了整体的装配效率。针对所存在的问题，本文基于着色Petri网(Color Petri Net, CPN)建模理论来构建一种面向低压电器的协同装配方法，并结合人工势场(Artificial Potential Field，APF)控制理论实现各装配单元的装配协同交互，提高低压电器装配的可重组性和动态响应能力。以协同装配时所能达到的装配效率最高、装配机器人数最低为目标，提出一种基于目标函数梯度的自适应量子遗传算法(Adaptive Quantum Genetic Algorithm，AQGA)对低压电器装配流程控制进行平衡优化。

1 基于CPN的协同装配建模

装配过程中，一个产品的装配是由许多个装配动作(例如：插、放、旋、压、粘、焊等)按一定顺序依次执行完成的。因此，在装配过程中，可以按照一定装配顺序来组合调度具有特定装配动作功能的机器人进行装配，并通过对不同功能的机器人进行装配顺序的重组，来实现对不同类型低压电器的快速有效的装配。基于上述思想，本文提出一种基于CPN的协同装配方法，所对应系统的整体构成如图1所示，整个装配系统主要由产品信息数据库、装配零件库、装配机器人库及机器人协同交互装配控制系统4部分所构成。在装配过程中，各部分根据自身的功能特点及产品的类型进行交互协同，实现产品装配。

由于低压电器的装配过程具有并行、异步、事件驱动、死锁和冲突等特征，整个协同装配系统是一个离散事件动态系统(Discrete Event Dynamic System, DEDS)[12-14]。该类系统的主要建模理论方法有：①图示—解析混合建模理论，其中具有代表性的有排队论、马尔科夫链及Petri-Nets建模理论等；②基于人工智能体的建模理论，其中具有代表性有多Agent系统、Holon整子系统；③粒度计算分析理论；④基于矩阵运算的建模理论等[15-16]。

本文基于低压电器的结构特点，采用CPN建模理论进行装配模型的构建。CPN不仅能清楚地反映出离散事件的先后、并行、同步与异步的特征，还能利用着色托肯对不同的装配任务及装配指令进行着色表示。CPN的形式化定义如下[17]。

定义1一个CPN是一个多元组CPN=(Σ，P，T，A，N，C，G，E，I)，满足下列条件：

(1)Σ为一个类型的非空有限集，这里称类型为颜色集；

(2)P为库所的有限集；

(3)T为变迁的有限集；

(4)A为弧的有限集，其中P∩T=P∩A=T；

(5)N为节点函数，其中N：A→(P×T∪T×P)；

(6)C为颜色函数，其中C：P→Σ；

(7)G为守卫函数，其中G：T→expr，且满足∀t∈T：[Type(G(t))=Bool∧Type(Var(G(t)))⊆Σ]；

(8)E为弧表达式函数，其中E：A→expr，且满足∀a∈A：[Type(E(a))=C(p(a)∧Type(Var(E(a)))⊆Σ]；

(9)I为初始函数，其中I：P→expr，且满足，∀p∈P：[Type(I(p))=C(p)MS∧Var(I(p))=Φ。

同时，根据协同装配系统的总体设计思想和CPN建模理论，应用CPN建模、仿真和分析工具CPN Tools对装配系统进行模型的构建。整个系统模型由2种类型的库所和6种类型的变迁所组成，各类库所及变迁的相关说明如下：

(1)零件装配状态信息库所定义PARTinform=productTASKNO×PART×ROBOT，其中product表示库所的数据类型为积颜色集;TASKNO表示零件装配的任务序列;PART表示所装配零件的类型及组合状态;ROBOT表示该零件装配所对应的机器人类型。该类库所主要用来表征各零件在装配过程所处的状态。

(2)装配指令变更库所定义ChangNO=productTASKNO×TASKadd×ROBOT，其中product表示库所的数据类型为积颜色集;TASKNO表示零件装配的任务序列;TASKadd表示下次装配的任务序列增值;ROBOT表示该装配零件后续装配所采用的装配机器人类型。该类库所是用来表征装配过程中系统的装配指令变更状态。

系统中的变迁包括：

(1)装配零件输送变迁 其输入输出的变量都为零件状态信息(n，p，r)，其中的变量定义如表1所示，所对应的库所为PARTinform。该变迁表示零件由零件存储库输送到个装配零件缓冲站中。

(2)装配零件状态转变变迁 其输入变量为组合前的零件状态信息(n，p，r)、(w，j，t),输出变量为零件组合后的组件状态信息(n，p^j，0)，其中的变量定义如表1所示，所对应的库所为PARTinform。该变迁表示两种零件装配成组件后的状态信息，并将机器人的分配任务数清零。

(3)装配信息发布变迁 其输入变量为组合后的零件状态信息(n，p，0)及装配指令信息(w，k，s)，输出变量为(n+k，p，s)，其中的变量定义如表1所示，所对应的库所分别为ChangNO及PARTinform，并设置守卫函数G：[n=w]。该变迁表示零件组合完后对其任务序列信息及相应的装配机器人信息进行重新设定。

(5)装配指令传递变迁 其输入输出变量均为零件的装配指令(w，k，s)，其中的变量定义如表1所示，所对应的库所分别为ChangNO。该变迁表示装配指令的先后传递顺序

(6)装配结束变迁 其输入输出的变量都为零件状态信息(n，p，r)，其中的变量定义如表1所示，其所对应的库所为PARTinform,并设置守卫函数G：[n=λ]，其中λ表示最后装配任务序列号。该变迁表示零件装配结束。

表1 CPN模型变量定义

因此，各类库所与变迁之间通过弧表达式的连接来构成装配系统中相应的功能单元，主要包含：零件库单元、装配机器人单元、装配控制单元、零件装配缓冲单元。相关结构构成如图2所示。

本文采用CPN仿真与分析软件CPN tools来对装配系统的CPN模型进行构建和仿真分析。根据图2所示的各装配单元及装配产品的装配任务序列，应用CPN tools对相应的装配单元进行构建和组合，来创建CPN模块化协同装配系统模型。假设某一产品的装配任务序列如如图3所示，其所需的装配机器人分别为R1、R2、R3,图3所示字母分别表示装配所要完成的任务，箭头表示各装配任务间的装配先后关系。根据图3中的各装配任务关系，假定该产品的装配顺序及机器人分配情况如表2所示，则应用CPN tools构建如图4所示模块化协同装配系统模型，所要装配的零件信息状态及控制信息指令分别用相应的托肯来表示(如表2)。

表2 产品的协同装配顺序

在零件信息状态托肯中，如(1,“a”,1)，括号里的第一个数字表示装配任务的序列号，第二个字母表示产品的装配组合状态，最后一个数字表示装配机器人的类型;在控制信息指令托肯中，如(1,2,2)，括号里的第一个数字表示所要进行控制的装配任务序列号，第二个数字表示将要变更的任务序列增量，第三个数字表示装配后所要指定的机器人类型，通过仿真分析最终生成的产品信息托肯如表3所示。由表3可知，最终产生的产品托肯为1`(7，“fcdbaeg”，3)，通过系统各单元间的协同装配，所装配完的产品数是1，最后的装配任务序列为7，产品的装配组合状态为“fcdbaeg”，完成最后装配的机器人类型为3。

表3 CPN装配模型中的托肯信息表

2 CPN装配系统控制优化算法

在协同装配系统中，有效地调度和协调各装配机器人按一定的装配顺序进行协同装配是产品装配成功与否的关键。为此，本文引入APF的控制理论来对机器人装配进行协同控制。APF主要基于引力场和斥力场的构建来实现移动机器人的避障[18-19]。基于APF的控制方法和原理，本文提出一种适用于协同装配控制的APF算法，相关数学模型定义如下：

假设在APF中，各模块化的装配机器人与所要完成的各装配任务(1个或多个装配动作)之间存在着势距ρi，

ρi=ωiηi。

(1)

式中：ωi为任务目标i在APF中所具有的位势;ηi为任务i在APF中所具有的场荷。

(2)

式中：mi为装配任务i的质量因子;t为完成该任务所需要的时间。

因此，定义在APF中任务i对装配机器人所产生的引力为Fi-att，斥力为Fi-rep，且

Fi-att=eρiμj，

(3)

(4)

则任务i对装配机器人所产生的势场合力

Fi-co=Fatt+Frep。

(5)

式(3)中μj为类因子,

(6)

其中α={1,2,3,…}为装配机器人功能模块号。

同时，场荷

(7)

APF在协同装配系统中的具体实现过程如算法1所示：

算法1APF在协同装配系统中的实现过程。

步骤1初始化各装配任务对机器人所产生的势场引力Fi-att=0，势场斥力Fi-rep=0。

步骤2分析计算势场中各装配任务所具有的位势ωi和场荷ηi。

步骤3计算各装配任务对机器人所产生的势场合力Fi-co=Fi-att+Fi-rep，其中产生最大势场合力Fco_max的机器人执行相对应的装配任务，并将该任务的位势和场荷归零。

步骤4再次分析计算势场中各装配任务所具有的位势ωi和场荷ηi；并重新计算未被执行的装配任务的势场合力Fi-co。

步骤5如果Fi-co=Fco_max则执行第i个装配任务，并且第i个任务的位势和场荷归零；否则继续搜寻Fco_max。

步骤6重复步骤2～步骤5，直到最后一个装配任务的位势，并使场荷归零，完成所有装配。

在协同装配系统中，针对所要完成的装配任务，在满足装配约束关系前提下，各装配任务的实现顺序不同，所需要的装配时间及装配机器人数也不同。因此，在协同装配系统中，针对低压电器的结构组合特点，需要对各装配机器人的调度及各装配任务的执行顺序进行平衡优化，以实现在最少的装配机器人数下，进行高效率装配(单个产品的装配时间达到最低)。为此，在APF的基础上，引入基于目标函数梯度的自适应量子遗传算法(Adaptive Quantum Genetic Algorithm, AQGA)对各装配机器人间的协同装配进行平衡优化。

量子遗传算法是一种基于量子计算理论与进化算法相结合的概率搜索优化算法，该算法用量子位编码表示染色体，用量子门作用和量子门更新完成进化搜索[20]。由于QGA具有种群规模小而不影响算法性能、收敛速度快和全局搜索能力强等特点，受到了国内外研究人员的广泛关注。本文则采用AQGA进行相关装配控制的优化，具体数学模型如下。

在QGA中，最小的信息单元用量子比特表示，一个量子比特的状态可表示为：

|Φj〉=αj|0〉+βj|1〉。

(8)

式中αj与βj满足

|αj|2+|βj|2=1，j=1,2,3,…,n。

(9)

同时将满足式(8)和式(9)的一对复数αj与βj称为一个量子比特的概率幅，并表示为[αj,βj]T。

在实数编码的量子遗传算法中，直接采用概率幅作为编码，具体编码方案如式(10)所示：

(10)

式中：θij=2π×rand，rand为(0，1)间的随机数;i=1,2,…,m；j=1,2,…,n；m为种群的规模，n是量子的位数。

假设优化变量求解范围为[Xmin，Xmax]，则由式(11)求解量子叠加的观测态：

qchi=

(11)

式中：i=1,2,…,m；j=1,2,…,n；m为种群的规模，n是量子的位数。

在量子相位旋转更新上，文献[21]提出了基于目标函数梯度的方法来控制旋转相位步长的大小如式(12)所示，本文在此基础上引入了基于最大波动均值的自适应函数来进一步控制步长的搜索精度(如式(13)所示)，避免搜索陷入局部最优的情况。

(12)

式中：sign(Comp)为相位转向函数，令ω0=[α0,β0]T为当前搜索的最优解的概率幅，ω1=[α1,β1]T为当前解的概率幅。则Comp=det(ω0,ω1)。

(13)

式中：k为自适应系数；aveg为均值波动函数，

aveg=max(δ1,δ2)。

(14)

其中：δ1为当前种群的适应度均值与适应度最小值之差的绝对值，

δ1=|mean(fit(qchi))-min(fit(qchi))|；

(15)

δ2为两代种群间的平均适应度之差的绝对值，

(16)

因此，改进后的量子相位旋转更新公式为

θ=θ0+Δθ1×Δθ2。

(17)

式中：θ为更新后的量子相位;θ0为原有的量子相位。

因此AQGA的具体实现过程如算法2所示：

算法2AQGA的实现过程。

步骤1初始化种群，确定种群大小n，量子位染色体位数m和量子变异概率Pm，包含n个个体种群Q={q1，q2，…，qn},其中qj为种群中第j个个体，具体描述如式(10)所示。

步骤2根据Q中各个体的概率幅，构造出量子叠加态的观测态Qchi，Qchi={qch1，qch2，…，qchn}，其中qchj为第j个(j=1,2,…,n)个体的观测状态，具体描述如式(11)所示。在QGA中，由概率幅Q构造观测态Qchi的过程包含解码过程，解码后得到各优化参数的实际值。

步骤3对观测态进行适应度评估计算，并计算最优值。

步骤4保留最佳个体，并判断是否满足终止条件，若满足，则算法终止;否则，执行步骤5。

步骤5根据式(17)计算量子旋转门的相位，并用式(17)中更新的量子相位作用于种群中所有个体的概率幅。

步骤6执行量子相位变异操作，产生新一代种群，并计算更新Qchi。

步骤7进行适应度评估计算，并计算相位更新变异后的最优解。

步骤8比较相位更新变异前后的最优解,若最优解退化则取回上代最优解;若最优解进化则将最优解替换。

步骤9进化代数增l，转步骤2继续执行，直到算法结束。

3 实验分析

为验证所提控制算法的有效性，本文以低压电器产品——1P断路控制器的装配为例来进行实验分析。本次实验所采用的计算机的处理器为：Intel(R)Core(TM)i5-6200U CPU @ 2.30 GHz 2.40 GHz,内存为4 G，实验平台是MATLAB R2012a。

1P断路控制器的具体结构及零部件的构成如图5所示，通过对其进行拆解分析可知，要完成该产品的装配，需要执行20个装配任务，每个任务用相应的字母进行表示，任务间的约束关联关系如图6所示，图中不同的图形表示要求实现的装配动作，每个装配任务旁边的括号里的数字表示完成该装配任务所需要的时间。在装配该产品的过程中，所需的装配功能包括有：插、放、旋、压、粘、焊6种功能，假定每种模块化的机器人只能执行两种装配功能，则在模块化协同装配系统中要装配完成1P断路控制器至少需要3台不同通过功能的机器人才能够实现。机器人与装配任务间的对应关系如表4所示。表中：Rp表示具有插、放功能的装配机器人；Rs表示具有旋、压功能的机器人；Rw表示具有焊、粘功能的装配机器人。

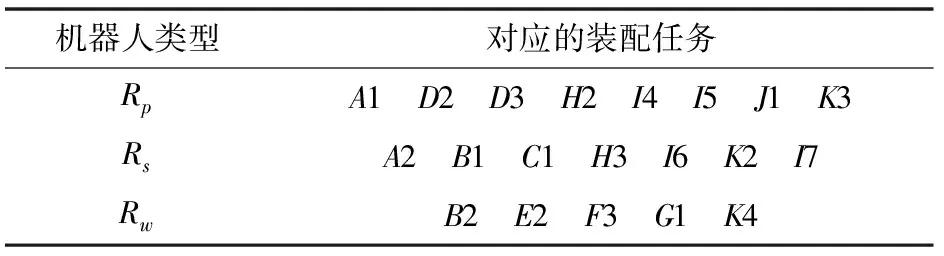
表4 各装配机器人所对应的装配任务

因此，在1P断路控制器的装配过程中，需要满足的要求如下：①装配过程中满足如图6所示的各装配任务间的装配约束关系；②装配过程中避免装配机器人及装配任务间的装配冲突；③避免调度过多的机器人，产生资源的浪费，要在最短装配时间下，实现所调用的机器人总数尽可能少。

因此，在实验分析中，先假定在装配机器人库中，随机选取的机器人数为N，N为任意的正整数,单个产品装配所需要完成的时间为t,同时将适应度评估值设定为

fit=f1×N+f2×t。

(18)

式中f1,f2为权重系数。为了均衡的考虑装配平衡优化对装配机器人数N及装配时间t的影响，将权重系数f1,f2都取为0.5。

为验证所设计的AQGA的有效性，本文引模拟退火遗传算法(Hybrid Genetic Algorithm combined with Simulated Annealing algorithm, GASA)[22]、QGA[21]及基于目标函数梯度的量子遗传算法(Quantum Genetic Algorithm based on Real encoding and Gradient information of object function, RG-QGA)与其进行优化效果的比较。所比较算法的相关参数设置如下:

(1)GASA：种群大小为40，最大遗传代数为20，个体变量维度为23，代沟为0.8，交叉概率为0.75，变异率为0.04。

(2)QGA：种群大小为40，最大遗传代数为20，个体变量维度为23，量子旋角为0.05×。

(3)RG-QGA：种群大小为40，最大遗传代数为20，个体变量维度为23，量子旋角为0.05×。

(4)AQGA：种群大小为40，最大遗传代数为20，个体变量维度为23，量子旋角为0.05×。

具体分析结果如图7所示。当N=25时，相比较于GASA、QGA、RG-QGA，AQGA的CPU运算时间最短，且不会陷入局部最优，能获得全局最优的值。最终通过AQGA求得适应度最优解为25.5，适应度均值的最优解为26，机器人数的最优解为6个，装配时间的最优解为45个时间单位。即在本例中，通过优化得出装配所需的机器人数至少为6时，才能实现在最短时间内完成装配(45个时间单位)。

为进一步验证所采用的AQGA的稳定性，将可选的机器人数N分别设为25台、50台、75台和100台，分别与GASA、QGA、RG-QGA进行比较，所优化比较的内容包括适应度最优值及机器人的最优个数，最终所得结果如图8和图9所示。

如图8和图9所示，从适应度值及机器人数的优化结果来看，随着机器人数的增加，GASA、QGA及RG-QGA在收敛的速度上逐渐变得缓慢，尤其是GASA、QGA两种算法陷入局部最优。而AQGA的收敛速度波动较小，并保持较快的速度进行收敛，不会因为机器人数目的增加而陷入局部最优。因此采用AQGA来进行装配控制优化较为适宜。

通过综合应用APF和AQGA进行机器人装配控制及优化后所得的最优装配序列如表5所示。表5中：Rp表示具有插、放功能的装配机器人；Rs表示具有旋、压功能的机器人；Rw表示具有焊、粘功能的装配机器人。

表5 优化后的1P断路控制器协同装配顺序

同时通过CPN中的仿真监控单元Monitor对各装配机器人所进行的装配任务数及相互间的装配协同情况进行分析观察，所得结果如表6所示。表6中Rp1_Task、Rp2_Task、Rs1_Task、Rs2_Task、Rw1_Task、Rw2_Task分别表示各装配机器人在装配过程中所属的装配任务。由表6可知，各装配机器人在装配过程中都能得到协同应用，没有出现装配闲置的情况。

表6 各装配机器人的装配协同分析结果

同时，考虑到产品装配过程中零件分发的随机性对各装配机器人装配任务接收及执行的影响，通过进行多批次仿真分析，并设定3个分别为90%、95%及99%的置信区间，对各类型的装配机器人所完成的装配任务协同的情况进行概率估计。如图11所示为进行5次仿真分析后，各机械人在不同置信区间下的装配任务数。由图11可发现，当置信区间为99%时，所包含的任务增加，但基本都在一个稳定的区间上徘徊，这在变批次的仿真分析中得到验证，具体如图12所示。

图12中所选的置信区间为95%，所设定的装配仿真批次数分别为5,10,15,20,25。由图12可以发现，在该装配系统的运行过程中，各机器人的装配任务数趋向稳定，并其同类型机器人间的装配任务数也基本趋向一致，即整个系统是逐步趋向装配平衡的。因此，所设计优化的装配控制方法是合理可取的。

4 结束语

由于低压电器产品的装配流程控制过程具有并行、异步、事件驱动、死锁和冲突等特征，本文应用CPN建模理论对装配系统进行建模，实现了对低压电器装配过程的有效模拟分析。

针对装配机器人间的协同交互控制问题，基于APF的相关控制原理，通过构建装配机器人与装配任务间的虚拟势场，使装配机器人与各装配任务进行相互的吸引或排斥，从而实现各装配机器人间的协同交互控制。

为使协同装配系统进行快速有效的装配，本文构建了一个面向1P断路控制器的协作装配实例，采用AQGA对求解收敛性、装配时间、装配机器人数等关键参数进行优化。与多种遗传算法(GASA、QGA、RG-QGA)进行比较可知，在适应度最优解、适应度均值、装配时间及装配机器人数的优化上，AQGA能够在第4代遗传种群后分别得到最优值25.5、26、45及6，而其他算法所要迭代次数较多，甚至会陷入局部的最优解。同时，应用所构建的CPN模型进行实验分析得出，通过APF及AQGA进行控制优化后，不同类型装配机器人各自所执行的装配任务数，在不同的仿真批次下基本趋于稳定，这表明所采用的APF及AQGA在低压电器的装配控制过程中较为稳定。因此，所构建的协同装配方法能够对低压电器进行稳定、高效的装配。

鉴于低压电器产品类型多样性的特点，下一步将对协同装配系统的装配共融性进行研究，使其能够同时处理不同类型的低压电器产品的装配，实现该类产品的多样化装配。