基于非参数误差模型的镜像铣同步精度补偿

郭景浩,张立强,王 勇,刘 钢

(上海工程技术大学 机械与汽车工程学院，上海 201620)

0 引言

近年来，随着航空航天、国防、装备等行业的飞速发展，生产加工过程日趋复杂化精细化，多机系统逐渐成为当前的研究热点[1]。和传统的单机系统相比，多机系统的复杂性存在更大的挑战[2]。浙江大学开发了一种新型的自动钻孔铆接系统[3]，该系统由两个协同五轴数控机床组成;法国的Dufieux公司开发了一种镜像铣削系统[4]，该系统主要用于蒙皮类零件的铣削加工。近几年，针对大飞机蒙皮件的加工，中航工业洪都引进了国内第一台镜像铣设备[5]，上海拓璞数控也研发了一系列镜像铣设备。多机系统的优势在于突破传统加工工艺局限性，使工件加工精度有了极大提升。

由于镜像铣系统中铣削侧和支撑侧在加工中会产生相对位置和方向误差，有可能导致严重的工件质量问题。如何有效提高镜像铣系统的相对位置和方向精度成为亟需解决的首要问题。误差防止法和误差补偿法是提高机床加工精度的两种常见方法[6]，其中误差补偿法主要分为基于模型的误差补偿和非参数误差补偿两类。基于模型的误差补偿主要经过误差模型的建立、误差的测量和辨识、误差的补偿等一系列过程，最终完成对误差的补偿，专家学者在近几十年对其进行了广泛的研究。Kim等[7]运用刚体动力学模型建立了五轴数控机床空间几何误差模型;Hsu等[8]假设机床是刚体，根据多体系统运动学利用四阶矩阵建立了一台两旋转三平动结构五轴数控机床的几何误差模型;Wu等[9]根据多体系统运动学理论，利用齐次坐标变化建立了非正交五轴数控机床的误差模型;杨建国等[10]对数控机床的几何和热综合误差进行了实时补偿。近些年，Fu等[11]、Bi等[12]很多学者对五轴数控机床几何误差的补偿进行了大量的研究。实际上，辨识所有的误差成分，并重复地计算误差模型的值是耗时且复杂的。为解决上述问题，很多专家提出了非参数误差补偿法，这种误差补偿方法主要包含误差预测和误差补偿两个过程。Wang等[13]提出一种多轴机床的基于形函数的误差预测方法和递归的软件补偿策略;之后周炜等[14]将非参数误差补偿法应用到机器人领域。上述方法是基于网格划分进行的误差预测，在误差预测环节需要大量的采样数据。Zhao等[3]提出一种钻孔铆接的双机系统，并针对该系统提出一种更加有效的误差预测方法，该方法的优点是采样数据少且精度高;之后，Zhao等[15]改进了之前的误差补偿方法，提出一种不同温度下的非参数误差补偿法。实验结果表明，非参数误差补偿法不但有效而且容易操作。研究人员对传统机床误差补偿的研究十分广泛，但是关于镜像铣加工同步运动精度补偿的研究非常少。为了减少镜像铣系统在加工过程的静态和准静态误差，本文采用非参数误差补偿法来提高镜像铣加工同步运动精度。

1 系统结构和运动学分析

1.1 系统结构

五轴镜像铣机床适用于运载火箭、飞机复杂曲面蒙皮和壁板铣削加工。五轴镜像铣机床由铣削侧和支撑侧两部分组成，如图1所示。其中：铣削侧是AC五轴卧式龙门结构，主要由X1轴、Y1轴、Z1轴3个平动轴和A1轴、C1轴两个旋转轴组成，装有高速电主轴，用于蒙皮壁板铣切和钻孔加工；支撑侧是AB五轴卧式龙门结构，主要由X2轴、Y2轴、Z2轴3个平动轴和A2轴、B2轴两个旋转轴组成，支撑装置中包括实时壁厚测量、阻尼支撑和激光测距等。

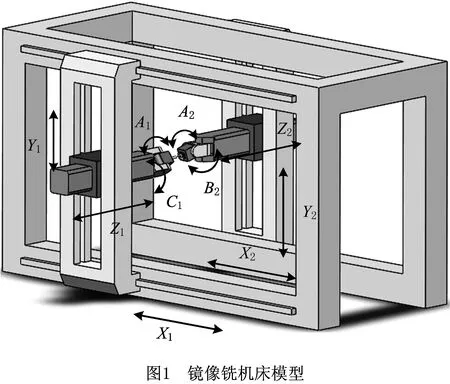
在铣削过程中，铣削装置和支撑装置分别位于工件两侧，经过一次装夹就可以完成全部的铣削加工工序，从而避免了工件经多次装夹所引起的装夹误差(基准不重合误差)，既保证了工件的最终加工精度，又提高了工件的整体生产效率。

1.2 运动学模型

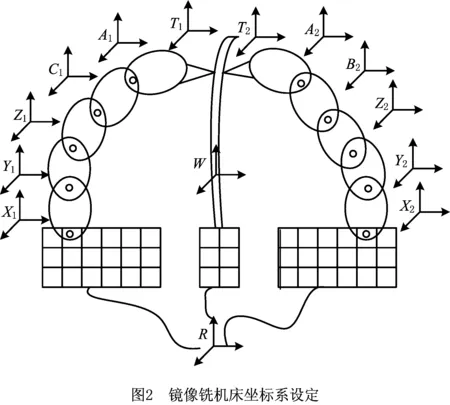
运动学分析需要镜像铣机床的综合运动学模型。为了清晰描述运动学建模过程，需要建立一些必要的坐标系。图1中，假设机床在初始状态下，机床床身创建参考坐标系R，在工件W上创建局部坐标系W，分别在铣削侧的X1、Y1、Z1向移动轴，A1、C1旋转轴和刀具T1上创建局部坐标系X1、Y1、Z1、A1、C1、T1，并且分别在支撑侧的X2、Y2、Z2向移动轴，A2、B2旋转轴和刀具T2上创建局部坐标系X2、Y2、Z2、A2、B2、T2，所有的坐标系方向和参考坐标系R一致，如图2所示。

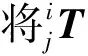
(1)

(2)

1.3 工作空间

在镜像铣加工过程中，任一点的刀尖点位置[px,py,pz]和刀具方向[wx,wy,wz]是我们需要的。因此，刀位点的位置向量为

pvi=[pxipyipziwxiwyiwzi]。

(3)

式中i=1,2，分别表示铣削侧和支撑侧。理论上，铣削侧和支撑侧刀位点的位置向量一致，但由于机床的几何误差、重力导致的误差和热误差等因素的影响，实际的铣削侧和支撑侧的刀位点位置向量会产生偏差。镜像铣机床铣削侧和支撑侧的相对位置和方向误差如式(4)所示：

E=pv1-pv2。

(4)

基于分解理论和叠加理论，将镜像铣机床的多维工作空间分为由3个平动轴组成的移动轴工作空间和由两个旋转轴组成的旋转轴工作空间，分别用WP和WR表示。在移动轴工作空间中，各旋转轴的值均为零；在旋转轴工作空间中，各平动轴的值均为定值。两个工作空间对机床的加工精度都会产生影响，则镜像铣机床的工作空间

W=WP+WR。

(5)

机床的几何误差、重力导致的误差和热误差等因素会造成铣削侧和支撑侧的相对位置和方向误差。误差

E=EP+ER。

(6)

式中EP和ER分别为移动轴工作空间和旋转轴工作空间下的相对位置和方向误差。在进行误差预测过程中，首先将镜像铣加工的整个多维工作空间分为移动轴工作空间和旋转轴工作空间两部分，然后在子工作空间中选取采样点、测量采样点处的误差，并通过插值公式计算任一点的误差，最终将子工作空间中得到的误差进行叠加，得到总的相对位置和方向误差。

2 误差预测

在误差预测阶段没有工件，因此两主轴理论上满足空间位置相同和同轴线。由上述内容可知，机床的移动轴和旋转轴都会造成误差，总的误差E由在移动轴工作空间的误差EP和在旋转轴工作空间的误差ER组成。因此，在工作空间的误差预测可以分为在移动轴工作空间的误差预测和在旋转轴工作空间的误差预测两部分。

2.1 移动轴工作空间的误差预测

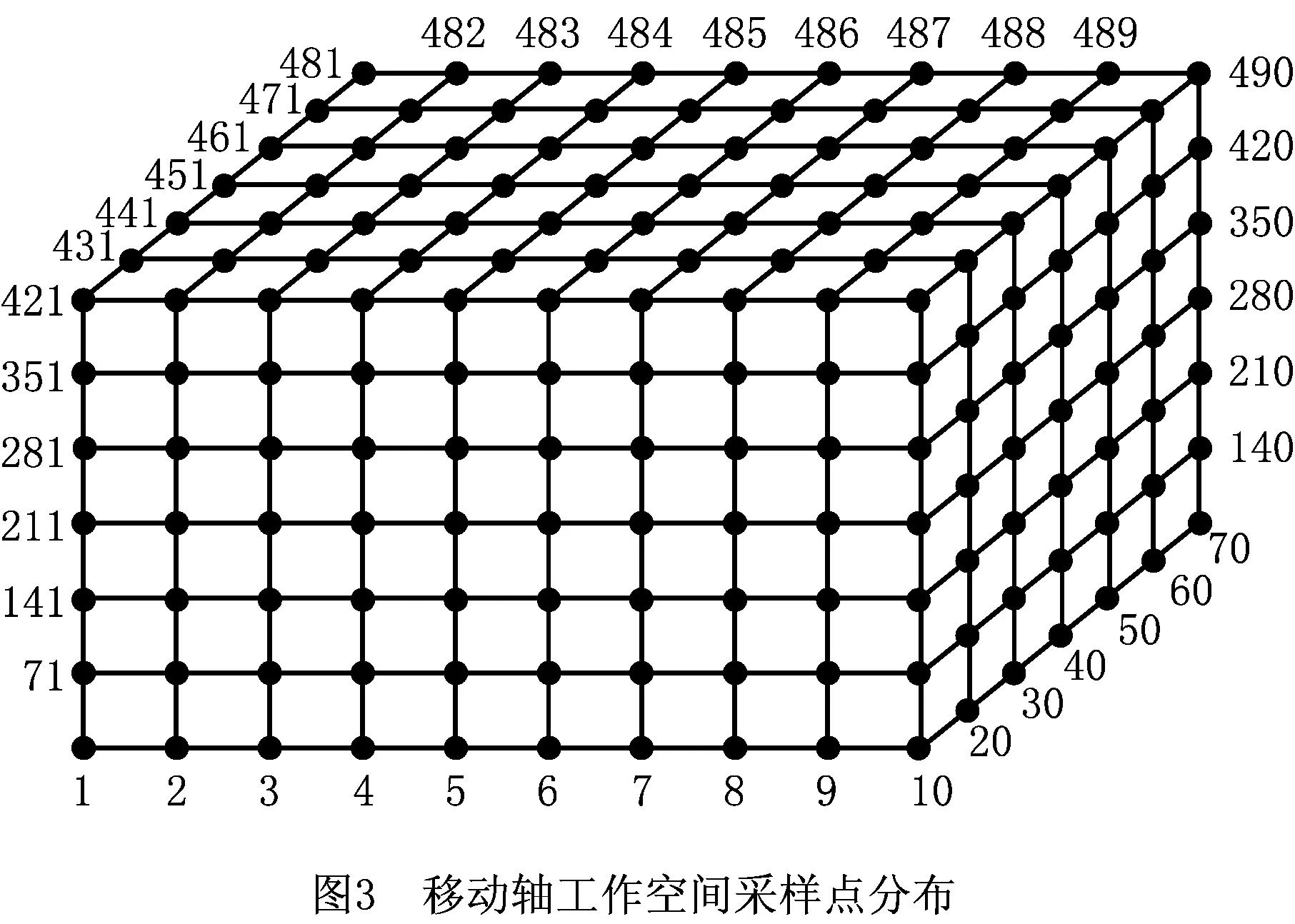
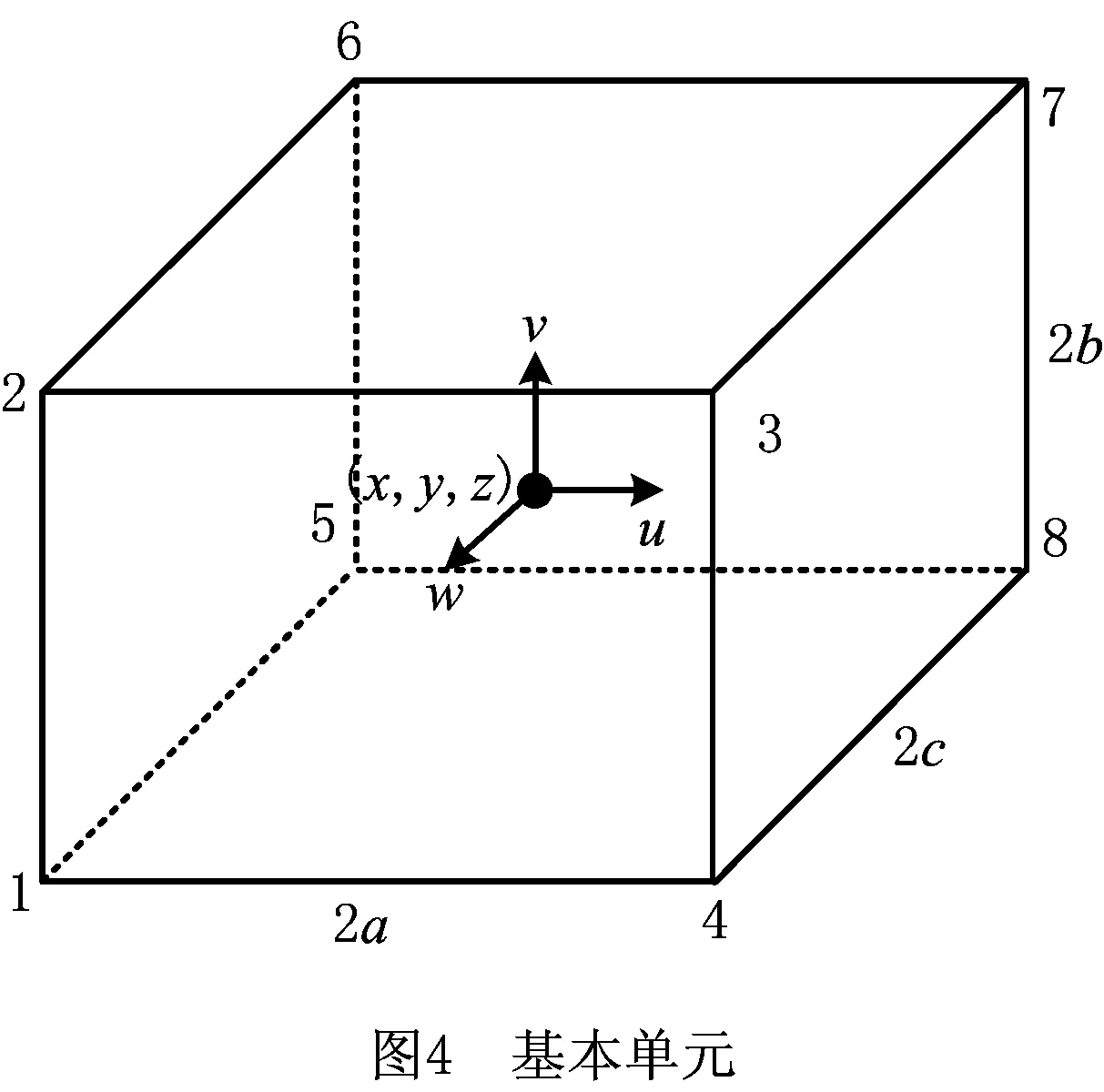
在移动轴工作空间的误差预测时，将铣削侧的旋转轴都置为0，只移动xyz轴。将整个工作空间在xyz方向均匀取点，假设共取10×7×7=490个点，如图3所示。其中每相邻的8个顶点围成一个立方空间，每一个立方空间称为基本单元，如图4所示。将铣削侧移动到这490个点的位置，且使支撑侧随动运行到和铣削侧相同的位置和方向，同时，利用激光追踪仪测量这490个采样点位置的铣削侧和支撑侧的相对位置和方向误差。基本单元的形函数如式(7)所示：

(7)

式中i=1,2,3,4,5,6,7,8;

由此得到移动轴工作空间的预测误差

(8)

式中：Mi为每个采样点的形函数，δi为每个采样点处的误差。在基本单元内任一点的相对位置和方向误差可以由式(8)插值得到。

2.2 旋转轴工作空间的误差预测

在旋转轴工作空间的误差预测时，将铣削侧的xyz轴设置为固定值，A轴和C轴的运动范围则构成了旋转轴工作空间，取一系列采样点在X-Y平面内的投影如图5所示。

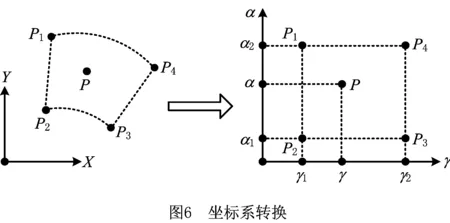
取图5中相邻的4个采样点或者3个采样点，将采样点转化到α-γ坐标空间下，如图6所示。其中：α表示A轴转过的角度;γ表示C轴转过的角度。图6中α-γ坐标空间下P1、P2、P3和P4围成的矩形的形函数如式(9)所示：

(9)

式中：j=1,2,3,4；

由此得到旋转轴工作空间的预测误差

(10)

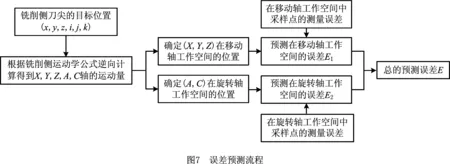
式中：Nj为每个采样点的形函数;ηj为每个采样点处的误差。任一点的相对位置和方向误差可以由公式(10)插值得到。将移动轴工作空间的预测误差EP和旋转轴工作空间的预测误差ER叠加得到总的预测误差E。误差预测的具体流程如图7所示。

3 误差补偿

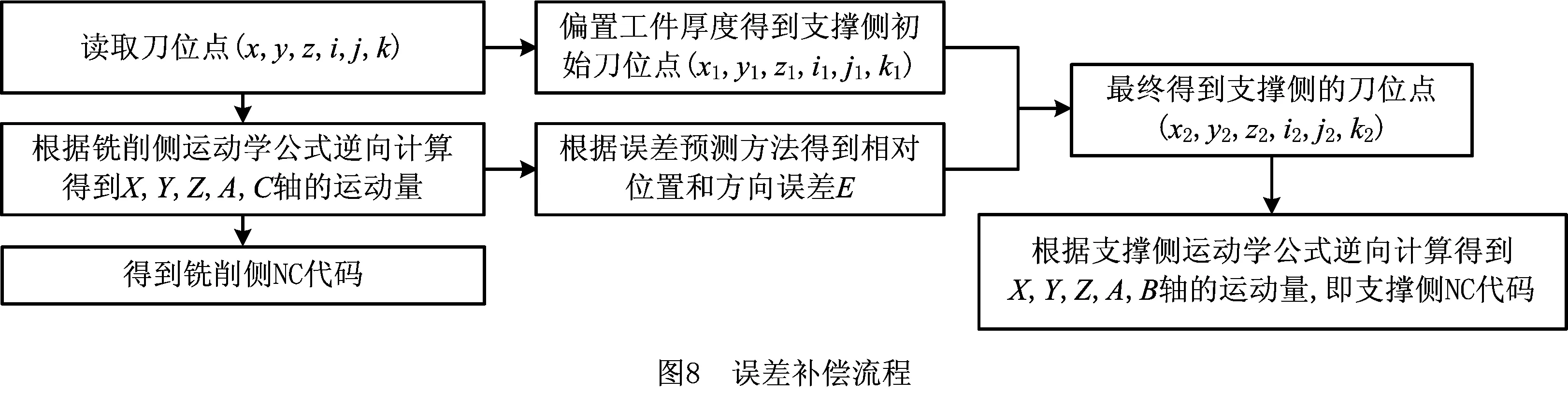
为了提高镜像铣机床铣削侧和支撑侧的相对位置和方向精度，下面介绍一种有效的误差补偿算法。铣削侧的绝对定位精度满足加工工件的要求，因此可以将铣削侧刀具的绝对位置和方向当作参考值。误差补偿策略是通过调整支撑侧的运动指令减小或消除在期望位置预测的铣削侧和支撑侧的相对位置和方向误差。

首先根据铣削侧的刀位点，利用误差预测算法预测铣削侧和支撑侧的相对位置和方向误差。然后，计算支撑侧调整后的位置向量为

(11)

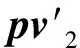
(12)

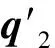
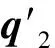
4 实验

为了验证本文的补偿算法的有效性和可行性，在如图9所示的实验平台进行实验。该实验平台分为镜像铣机床和激光跟踪仪两部分，镜像铣机床由铣削侧和支撑侧组成，激光跟踪仪的绝对测量精度为±10 um/m和重复测量精度为±5 um/m。实验分为确定采样点数量和验证补偿算法的有效性两部分内容。

在进行误差预测前，必须先确定移动轴工作空间和旋转轴工作空间的采样点数量。一般来说，采样点的数量越多，误差预测精度越高。但是如果采样点的数量过多，误差的测量和计算将花费大量的时间，则误差补偿的效率就会降低。需要根据误差预测精度选择合适的采样点数量，其中误差预测精度是真实误差与预测误差之间的偏差值，用p和θ表示误差预测精度：

p=

θ=

(13)

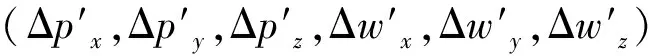
表1 移动轴工作空间中不同数量采样点的预测精度

表2 旋转轴工作空间中不同数量采样点的预测精度

为了验证本文误差补偿算法的有效性，在镜像铣机床的工作空间内均匀选择30个校验位置进行实验验证。当机床运行到每个校验位置时，使用激光跟踪仪测量该位置未补偿的相对位置和方向误差，并运用误差预测算法预测该位置的相对位置和方向误差。然后，经过实现补偿算法的后置处理得到补偿后的支撑侧的NC代码，再次运行机床运动到上述30个校验位置，同时使用激光跟踪仪测量校验位置补偿后的相对位置和方向误差,30个校验位置的未补偿误差、预测误差和补偿后的误差如图11所示。本文用Δp和Δθ分别表示相对位置误差和相对方向误差，

Δp=

Δθ=

(14)

式中：(px1,py1,pz1,wx1,wy1,wz1)和(px2,py2,pz2,wx2,wy2,wz2)分别为铣削侧和支撑侧的刀位点向量。

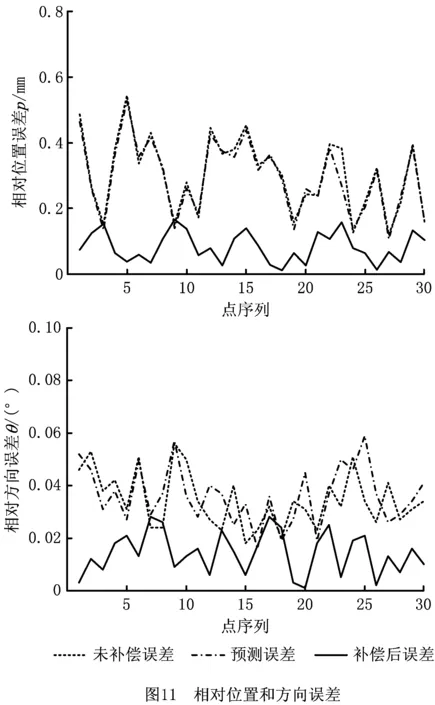
从图11中可以看出，实际测量的未补偿误差和预测误差之间的偏差很小，两种误差甚至在很多点处接近相同，这说明在移动轴工作空间和旋转轴工作空间选择的采样点数量是合适的。对图11中的30组数据进行统计分析，统计结果如表3所示。从表3中可以得到，经过误差补偿，铣削侧和支撑侧的平均相对位置误差从Δp=0.304 mm降到Δp=0.082 mm，平均相对方向误差从Δθ=0.035°降到了Δθ=0.014°。并且补偿后的最大相对位置和方向误差为Δp=0.165和Δθ=0.028°，满足镜像铣加工的精度要求，从而证明了本文提出的误差补偿算法的有效性和可行性。

表3 相对位置和方向误差分析结果

5 结束语

为了提高镜像铣机床铣削侧和支撑侧的相对位置和方向精度，本文提出一种有效的误差补偿方法，该误差补偿法主要由误差预测和误差补偿两部分组成。在误差预测过程中，将镜像铣系统的多维工作空间分为移动轴工作空间和旋转轴工作空间，且分别研究两个工作空间各自对目标误差的影响。通过激光跟踪器测量采样点处的误差，应用一种基于形函数的插值算法能够预测镜像铣工作空间中任意期望位置的相对位置和方向误差。在误差补偿过程中，将铣削侧的刀位作为参考值，利用误差预测算法的得到的误差值支撑侧的刀位进行误差补偿，然后分别生成NC代码。经过加工测量实验，补偿后的相对位置和方向精度分别提高了73%和60%，从而验证了该算法的有效性和可行性。该补偿算法不仅能够满足加工精度要求，还减少了采样点的数量从而节省了补偿的时间。未来可进一步考虑刀具几何误差、机床伺服系统误差和工件定位误差等，建立一个更全面的综合误差模型。