微机电系统产品非正态多质量特性的稳健设计方法

吴佳伟，宋华明+，万良琪，黄 甫，马东升，杨加猛

(1.南京理工大学 经济管理学院，江苏 南京 210094；2.南京航空航天大学 经济与管理学院，江苏 南京 211106；3.南京林业大学 经济管理学院，江苏 南京 210037)

0 引言

微机电系统(Microelectro Mechanical Systems, MEMS)产品凭借其高灵敏度、小体积、低能耗等优点已被广泛应用于姿态测量、气象探测、飞行器控制与导弹精确制导等领域[1-3]，MEMS产品的稳定性对精密仪器的可靠性和使用寿命具有很大影响。由于MEMS产品微结构尺寸的特殊性，使得传统机械产品工作中被忽略的温度噪声往往在MEMS产品中具有显著影响，持续热量接触面和非接触面产生的截面温差造成MEMS产品主体结构参数具有一定的随机性，导致MEMS产品非正态多质量特性产生波动。而学者们对温度噪声和设计参数随机性下的微观结构运动规律缺乏充分的统一认识，为此，在微观结构稳健优化理论尚未成熟的情况下，如何有效运用当前设计理论方法支持MEMS产品非正态多质量特性稳健设计，是MEMS产品质量工程急需解决的关键科学问题。

国内外众多学者开展了MEMS产品结构优化和质量特性设计研究[4-5]。Ayanoor-Vitikkate等[6]将薄膜封装技术应用在MEMS产品结构设计中，降低了设计成本并提高了MEMS产品质量特性稳定性;Ghayesh等[7]研究了非线性、小尺寸效应、平面惯性及位移等因素对MEMS产品质量特性影响，根据Kirchhoff薄板理论和拉格朗日方程构建了MEMS产品非线性质量特性模型;Torabi等[8]采用系统识别技术将MEMS产品非线性质量特性设计问题转化为线性稳健优化问题，通过仿真研究表明了该方法的有效性;Asano等[9]对不同镀金薄膜的微悬臂梁进行弯曲试验，有效解决了MEMS产品因微悬臂梁脆性断裂和应力过大而造成质量特性失效的难题。虽然采用封装处理技术和实验方法在一定程度上可以解决由于决策者缺乏微观结构真实信息的知识而带来MEMS产品质量特性设计上的不确定性问题，但忽略温度噪声对质量特性的影响会降低优化设计效果。

实际工程中，温度噪声会对硅微敏感结构产生显著影响，继而降低MEMS产品整体性能[10-11]，常用的解决方法和不足之处包括：材料的改进，但实现途径成本较高；温度补偿，但难以在较短时间内提升MEMS产品质量特性；温度控制，只适应于实验重复性较好的MEMS产品。稳健设计理论的发展为弥补上述方法的不足并提高MEMS产品整体性能提供了新思路。Dwivedi等[12]针对折叠式MEMS加速度器进行稳健设计，通过主体结构的几何尺寸参数获得满意质量特性，并通过仿真分析验证了该方法的有效性;Liu等[13]探究了不同温度下MEMS开关的质量特性规律，通过优化主体结构和底座厚度实现质量特性稳健;Chen等[14]结合硅蚀刻技术和仿真提出一种薄膜封装新工艺，在温度噪声下通过提供稳定的运行环境来保障MEMS产品工作稳定性;Liu等[15]为解决温度噪声带来的MEMS传感器质量特性波动难题，通过建模分析提出一种温度补偿方法。以上学者将温度噪声考虑到MEMS产品设计中，能够保证其质量特性的稳健可行性。

上述文献虽然指出温度噪声对MEMS产品质量特性造成显著波动，但如何通过改进结构设计来降低温度噪声引起质量特性波动的深入研究不多。Liu等[16]考虑温度噪声提出一种基于灵敏度分析的MEMS加速度器稳健设计方法，并给出改进方案。在热变形作用下几何结构的概型分布也会改变，仅作正态假设会导致信息失真，而对此学者未予以足够重视。Kim等[17]研究了温度噪声影响下采用封装技术并设计适合结构来保证MEMS振谐器的稳健性，该研究不足之处在于设计过程中无法给出支持质量特性正态分布假设的证据，设计时采用正态分布将导致服役时间越长，MEMS振谐器质量特性越无法满足工作需求。工程实践中由温度噪声引起MEMS产品质量特性概率分布复杂，MEMS产品主体结构热变形使得设计参数发生不同程度的随机变化，已有研究构建的模型难以揭示复杂机理。目前，通过广义线性模型来描述MEMS产品非正态多质量特性的变化规律，并提出质量特性稳健设计策略的相关研究尚无报道。

综上所述，本文针对温度噪声和设计参数随机性下MEMS产品非正态多质量特性稳健设计问题，建立了基于广义线性模型框架下的非正态多质量特性均值模型和方差模型。本文所提方法具有如下特点：将非正态多质量特性方差作为稳健性指标，同时考虑MEMS产品功能满意；综合考虑了非正态多质量特性之间的稳健性权衡；利用模糊满意决策理论处理Pareto最优解的方案优选问题。同时，本文还提出了基于分解的多目标进化算法(Multi-Objective Evolutionary Algorithm based on Decomposition，MOEA/D)的MEMS产品多质量特性优化策略。通过算例表明，所提方法有效地提高了MEMS产品非正态多质量特性的稳健性。

1 MEMS产品质量特性波动问题描述

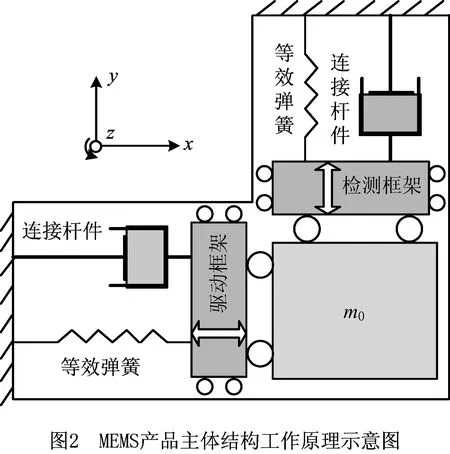
MEMS产品主体结构由机械敏感结构的硅材料、弹性元件、驱动模块和检测电路组成，如图1所示。弹性元件与驱动模块将力或能量转换成位移信号，检测电路提取输入信号和输出信号。MEMS产品工作时，驱动框架会在外部静电力作用下带动质量块m0沿x方向运动，角速度z不为零时质量块m0带动检测框架沿y方向运动，其工作原理如图2所示。在不受外部冲击或振动情形下，MEMS产品主体结构沿x方向输出位移为[18]：

s0=Fdsin(ωdt0+φx0)/(m0ωO)+

(1)

该模型在理论研究中具有极高的精度，但不能很好地满足复杂工程实践和工业应用要求，这是因为MEMS产品受到来自设计阶段无法预见的不确定性因素影响，尤其是温度噪声引起温度梯度导致结构内部出现热应力，致使MEMS产品质量特性出现波动，而制造设备和现有技术条件也制约着MEMS产品加工精度，仅着眼于理论模型研究在一定程度上存在质量特性模型精度不高、误差较大和质量特性不够稳定等不足之处，不符合现代设计理念。因此，有必要构建更高效、更高精度、更具适用性的模型。本文将在仿真分析的基础上建立MEMS产品非正态多质量特性模型并引入温度噪声，为后续MEMS产品稳健设计奠定基础。

2 基于广义线性模型的MEMS产品非正态多质量特性模型的构建

温度噪声和设计参数随机性情形下，MEMS产品非正态多质量特性变化规律难以确定，构建多质量特性模型是研究MEMS产品稳健设计所面临的工程科学难题，其模型的准确性直接影响输出精度、主体结构可靠性和稳健性，因此采用本文提出的广义线性模型解决非正态多质量特性建模问题，寻找降低温度噪声影响的可控因素的实施条件。

若记R和Φ分别为MEMS产品非正态多质量特性联系函数的均值模型和方差模型，则有：

R=ω(μ)=X′α，

(2)

(3)

式中：ω和η为广义线性模型的线性预测器;X为MEMS产品主体结构设计参数；α为MEMS产品主体结构设计参数的系数；Tz和γ为温度噪声及其系数。

根据联系函数和响应曲面模型[19]分别构建MEMS产品非正态多质量特性均值模型和方差模型为：

(4)

VarTz(yk)=VarTz[E(yk|Tz)]+ETz(εijV(μ))。

(5)

式中:α0为常数项；ξ为MEMS产品设计参数和温度噪声之间的交互系数；yk为MEMS产品第k个非正态质量特性。

运用泰勒公式对参数εijV(μ)进行近似展开，对MEMS产品非正态多质量特性取温度噪声Tz的期望，进一步得到MEMS产品非正态多质量特性均值模型和方差模型为[20]：

VarTz(R),

(6)

(7)

(8)

MEMS产品非正态多质量特性均值模型和方差模型中的未知参数γ估计过程类似。至此，柔顺精密产品非正态多质量特性均值模型和方差模型构建完成，广义线性模型的运用为解决温度噪声下MEMS产品非正态多质量特性稳健设计问题的分析提供强有力的工具和方法，本文将运用MOEA/D对构建的模型进行优化。

3 基于MOEA/D方法的MEMS产品非正态多质量特性优化

MEMS产品非正态多质量特性均值模型和方差模型包含多个相互冲突的目标函数[21]，存在能同时较好地满足各目标函数的一组非劣均衡Pareto最优解[22]，优化过程主要分为两步：①采用MOEA/D获取分布均匀的多质量特性Pareto解集；②运用模糊满意决策理论在Pareto解集中找到符合设计要求的最优折中解。MOEA/D将逼近整个Pareto最优前沿的优化问题分解为一定数量的单个质量特性优化子问题，采用对前沿面形状不敏感且计算简便的Tchebycheff分解策略，其模型为：

s.t.

X∈Ω;

(9)

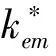
步骤3对j∈B{k*}，若gte(fy′|λ′,p*)≤gte(xj|λj,p*)，则xj=fy′，F(xj)=F(fy′)。

步骤4从EP中删除被F(fy′)支配的向量，若EP中无支配F(fy′)的向量，则将F(fy′)加入EP。

步骤5若满足预先设定的停止判据，则停止并输出种群，否则返回步骤2。

MOEA/D对各子问题进行协同进化和均匀分布的权重向量引导种群进化，降低MEMS产品非正态多质量特性优化复杂度和提高搜索能力且获得均匀分布解集。为进一步确定最优折中解，引用模糊满意决策理论进行筛选[23]，非正态望大质量特性的Pareto最优解对应模糊隶属度函数为：

FDMi(yk)=

(10)

非正态望小质量特性的Pareto最优解对应模糊隶属度函数为：

FDMk(yk,i)=

(11)

MEMS产品非正态多质量特性的每个非劣解的满意度最大值即为最优折中解，每个非劣解的满意度评价为：

(12)

综上所述，本文考虑温度噪声和设计参数随机性下的MEMS产品非正态多质量特性稳健设计框架如图3所示。

4 实例分析

4.1 MEMS精密陀螺有限元分析与模型构建

MEMS精密陀螺作为MEMS产品主要代表，其工作原理是在静电梳齿驱动下，质量块发生运动来完成功能需求，如图4所示。由于温度引起热变形和设计参数具有随机性，导致MEMS精密陀螺非正态多质量特性波动。为解决该实际工程难题，在本文所提的广义线性模型下引入响应曲面来构建非正态多质量特性均值模型和方差模型，对MEMS精密陀螺非正态多质量特性进行稳健设计。设计目标是通过选择合适的结构尺寸，使得温度噪声和设计参数随机性下的MEMS精密陀螺主体结构应力和输出位移变化范围越小越好，同时应力值尽量小且输出位移值尽量大。

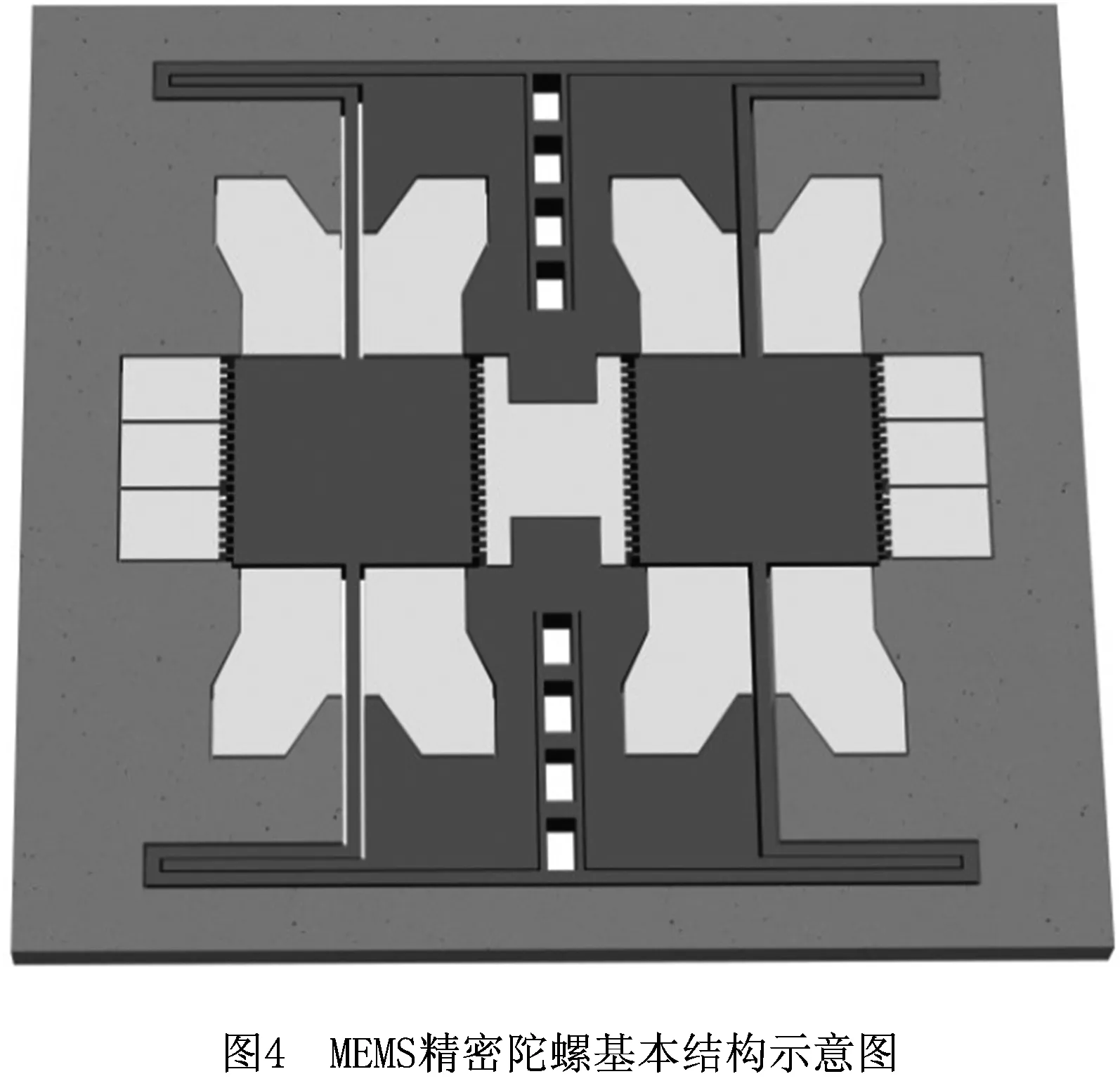
假定MEMS精密陀螺主体结构有限元模型所有节点在等效温度载荷作用下的变形和实际模型热载荷作用下变形相同，热环境下对应力和输出位移进行有限元分析，利用Solid45模型建立了MEMS精密陀螺的ANSYS模型，网格划分最小单元设置为0.05 mm，两端施加固定的边界条件，如图5所示，其中质量块参数为x1，柔性元件宽为x2，主体结构厚度为x3。

结合有限元分析和试验设计，将大幅度提高MEMS精密陀螺非正态质量特性稳健设计效率。研究表明，模型预测精度主要取决于试验设计，因此采用均匀性较好的拉丁方设计[24]来选取30组样本点，用于构建MEMS精密陀螺非正态多质量特性均值模型和方差模型，运用有限元分析实现应力yτ和输出位移ys的数值模拟，结果如表1所示。

表1 MEMS精密陀螺拉丁方设计方案

(13)

(14)

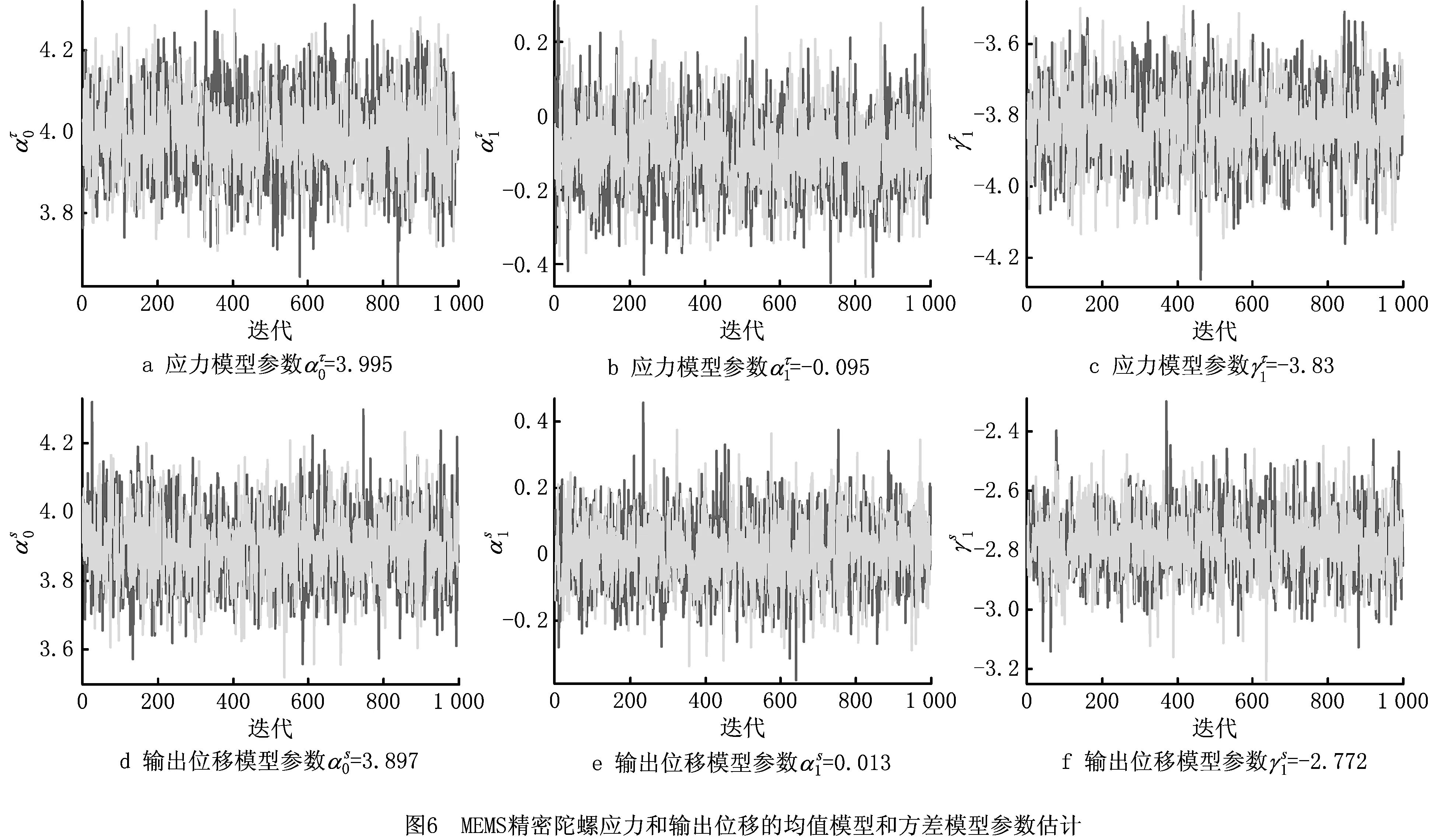
根据式(6)和式(7)建立MEMS精密陀螺应力和输出位移的均值模型和方差模型，并运用贝叶斯推断式(8)处理模型中未知参数的估计问题，限于篇幅，仅列出应力和输出位移均值模型和方差模型中α0、α1、γ1估计值，结果如图6所示。

采用贝叶斯方法确定MEMS精密陀螺非正态多质量特性均值模型和方差模型的参数值，则MEMS精密陀螺应力对设计参数x1、x2、x3、温度噪声Tz的均值模型和方差模型分别为：

(15)

e(4.16-0.19x1-1.284x2+0.144x3)×

(16)

MEMS精密陀螺输出位移对设计参数x1、x2、x3和温度噪声Tz的均值模型和方差模型分别如下：

(17)

(18)

表2 MEMS产品应力和输出位移模型精度检验

(19)

(20)

4.2 MEMS精密陀螺稳健设计结果

针对MEMS精密陀螺应力和输出位移的均值模型和方差模型的优化问题，利用MOEA/D解决多质量特性相互冲突、离散和温度噪声条件下的模型求解难题。MEMS精密陀螺应力和输出位移稳健优化模型分别为：

(21)

(22)

基于MOEA/D方法的MEMS精密陀螺应力和输出位移稳健优化模型为：

findx=[x1,x2,x3]，

min[F(yτ),F(ys)];

(23)

根据MOEA/D方法获得MEMS精密陀螺应力和输出位移的稳健优化模型的Pareto最优解，结果如图7所示，应力和输出位移Pareto最优解如图8所示。

由此可知，随着MEMS精密陀螺应力的改善，输出位移不断下降，因而并不存在使两者同时达到最优的唯一解。根据模糊满意决策理论式(10)～式(12)对Pareto最优解进一步筛选出最优折中解，该最优折中解经反归一化式(14)处理后获得最终设计参数为x1=2.4 mm，x2=0.28 mm，x3=0.95 mm，yτ=40.88 MPa，ys=40.25 μm。

4.3 MEMS精密陀螺稳健设计结果验证分析

findx=[x1,x2,x3],

(24)

根据MOEA/D方法求解式(24)中的确定性优化模型，结果如图9所示，为便于比较，同时将4.2节中的MEMS精密陀螺稳健设计结果绘制于图9中。由图9结果可知，相同条件下MEMS精密陀螺确定性优化获得的Pareto前沿大都优于稳健设计，这是由于在稳健设计中考虑了温度噪声和设计参数随机性。为确保获得稳健解而损失了MEMS精密陀螺部分质量特性指标，使得设计变量对变差灵敏度较小，保障了优化解的稳健性。

综合MEMS精密陀螺初始方案、确定性优化方案及本文方案进行对比，采用蒙特卡罗法和有限元分析对初始方案和确定性优化方案进行稳健性评估。为叙述方便，初始方案称为方案1、确定性优化方案称为方案2，图10给出了3种方案下设计变量对多质量特性变异系数的影响，表3给出了3种方案的相关参数结果。

表3 MEMS精密陀螺设计方案结果对比

由图10a和图10b结果可知，设计变量x1在不同取值下，相较于初始方案和确定性设计方案，本文方案的MEMS精密陀螺应力和输出位移的变异系数均较小，变异系数越小表明质量特性对设计参数变化越不敏感，质量特性越稳健，这与本文方案同时考虑了温度噪声和设计变量随机性有关;图10c～图10f同样表明本文设计方案显著优于初始方案和确定性设计方案。此外，设计变量最优解不代表多质量特性变异系数小，而设计变量稳健解则能够获得较小的多质量特性变异系数，稳健解能够增强质量特性抵抗参数变化的能力并降低对参数的敏感度。

从表3结果来看，稳健设计方案比初始方案的MEMS精密陀螺应力值降低了1.11%，输出位移增加了14.28%，这是应力和输出位移之间权衡的结果，更重要的是应力标准差下降了37.39%，且输出位移标准差下降了43.1%。确定性优化是应力和输出位移同时趋近于各自最优值，进而达到综合性能最优效果，因而确定性优化结果总体上显著优于稳健设计。确定性优化模型中未考虑温度噪声和设计参数随机性造成目标函数的摄动，尽管确定性优化结果较优，但在温度噪声和设计参数随机性影响下，其有效性和可靠性可能大幅度下降，甚至不可信，而本文所提方法的优化结果和确定性优化相比，MEMS精密陀螺应力和输出位移的标准差分别降低43.41%和37.52%，使MEMS精密陀螺总体性能稳健性显著提升。

4.4 MEMS精密陀螺可靠性验证分析

为分析稳健设计后MEMS精密陀螺的可靠性，采用蒙特卡罗法估计MEMS精密陀螺失效概率，结果如图11所示。随着样本量的增加，失效概率估计值逐渐趋于平稳，当样本量为2 500时，MEMS精密陀螺失效概率估计值达到平稳状态，结果表明初始方案的失效概率为0.045 2，稳健设计方案的失效概率为0.008 8。由此可知，采用本文所提方法进行稳健设计，MEMS精密陀螺的可靠度由95.48%提升到99.12%(增幅3.64%)，满足工程实践应用要求。

分析结果可知，在MEMS精密陀螺稳健设计中，几何尺寸、工艺参数等细节因素对结构可靠性具有至关重要的影响，合理的结构与良好的工艺设计可以极大地提高MEMS精密陀螺稳健性与可靠性。进一步对图11进行分析，发现无论样本量多少，稳健设计得到新结构的失效概率始终低于初始结构，特别是样本量较少时，这种优势更明显。这表明考虑温度噪声和设计参数随机性下的MEMS精密陀螺非正态多质量特性稳健设计对于提高主体结构的可靠性具有重要实际意义。此外，使MEMS精密陀螺可靠性降低的温度因素有：①热环境下薄壁结构易发生屈曲和大位移变形；②温度变化加快主体结构材料的退化速度；③热应力对结构内部振动会产生较大的负面影响。本文所提的设计方法能将上述温度因素考虑在内，从而使新结构的可靠性得到大幅度的提升。

综上所述，MEMS精密陀螺非正态多质量特性稳健设计显著改善了综合性能稳健性，并提高了结构可靠性。

5 结束语

本文研究了温度噪声和设计参数随机性下的MEMS产品非正态多质量特性健性设计问题。首先通过广义线性模型构建了非正态质量特性均值模型和方差模型；然后采用MOEA/D方法进行优化求解，获得了满意的优化结果。通过MEMS精密陀螺稳健设计算例分析，得到如下结论：MEMS精密陀螺应力降低了1.11%且输出位移提升了14.28%，更重要的是应力标准差降低了37.39%且输出位移标准差降低了43.1%，优化后得到的新结构可靠性提高了3.81%。因此，所提方法应用于温度噪声和设计参数随机性下的非正态多质量特性稳健设计，可有效地改善MEMS产品质量，为从事微观结构设计工作者提供极大便利。

本文主要采用有限元分析和蒙特卡罗模拟对优化结果进行验证，优化效果在实际环境中是否明显尚需通过实验进一步分析。因此，将实验与理论优化相结合是今后展开动态随机噪声条件下MEMS产品稳健设计工作的另一个重点。