椭圆曲线整数点的递推序列及二次剩余法求解

董 鑫,牟全武

(西安工程大学 理学院,陕西 西安 710048)

0 引言与主要结果

椭圆曲线是亏格为1的代数曲线,至少有一个已知点。根据Riemann-Roch定理,在同构意义下有理数域上任一椭圆曲线的方程总可以化为Weierstrass方程E:y2=x3+Ax+B,这里A与B为有理数。方程E的判别式定义为Δ=-16(4A3+27B2)。当A与B为整数且判别式Δ非零时,由Siegel定理知，在椭圆曲线E上只有有限个整数点。尽管人们已从Mordell-Weil定理[1]知椭圆曲线E上所有有理点构成的集合是有限生成的Abel群,但在一般情形下要求出具体的有理点或整数点，仍是数论中十分困难的问题,至今没有得到完全解决。针对某些特殊的椭圆曲线,国内外学者已得到不少结果[2-13]。

在文献[14]中,Zagier给出了寻找有理数域上的椭圆曲线大整数点的3种方法；Zagier还构造了一批有大整数点的椭圆曲线。例如，椭圆曲线

y2=x3+27x-62

(1)

有大整数点

(x,y)=(28 844 402,±154 914 585 540)

椭圆曲线

y2=x3-30x+133

(2)

有整数点(x,y)=(5 143 326,±11 664 498 677)。

文献[15]用代数数论及p-adic分析方法给出了椭圆曲线(1)的全部整数点;文献[16-17]根据四次丢番图方程的已知结果,对文献[15]的结果分别给出了简化证明。文献[18]证明了以下结果:

定理1椭圆曲线(2)的所有整数点是

(x,y)=(-7,0),(-3,±14),(2,±9),(6,±13),

(5 143 326,±11 664 498 677)

由于文献[18]的证明需要在一类全虚四次域的子环上讨论二次代数整数的分解并计算其单位,所以证明过程比较复杂。 在文献[19-20]中, 罗明通过改进Cohn的递推序列方法[21], 先后解决了Fibonacci数列和Lucas数列中的三角数问题, 后来他又用这一方法解决了Lucas数列中的五角数问题[22]。 这些工作显示了递推序列方法在解决一些困难的数论问题时十分有效。 受文献[19-20]及[22]证明思想的启发, 本文利用递推序列及二次剩余给出了定理1的初等证明。

1 若干引理

xn=5un+26vn,zn=-21un+78vn

(3)

容易验证下列关系式成立:

un+2=1 298un+1-un,u0=1,u1=649

(4)

vn+2=1 298vn+1-vn,v0=0,v1=180

(5)

(6)

un≡1(mod 24),un≡±1(mod 13),

u2n≡1(mod 5)

(7)

u2n+1≡0(mod 11),u8n+1≡3(mod 17),

u8n+5≡-3(mod 17)

(8)

u8n≡1(mod 17),v8n≡0(mod 17),

v4n+3≡-4(mod 11)

(9)

v8n+1≡-7(mod 17),v8n+5≡7(mod 17)

(10)

引理1∀n,k,m∈N+,有

un+2km≡(-1)kun(modum)

vn+2km≡(-1)kvn(modum)

(11)

0(modum)

(12)

un+2km=Aun+13Bvn≡(-1)kun(modum)

vn+2km=Avn+13Bun≡(-1)kvn(modum)

引理1得证。

由式(3)及引理1可得如下的推论：

推论1∀n,k,m∈N+有

xn+2km≡(-1)kxn(modum),

zn+2km≡(-1)kzn(modum)

(13)

x2m(4k+1)≡x2m(modu2m),

x2m(4k+3)≡-x2m(modu2m)

(14)

z2m(4k+1)≡z2m(modu2m),

z2m(4k+3)≡-z2m(modu2m)

(15)

引理2如果m>0且8|m,那么

证明当m>0且8|m时,由式(6)与(7)得

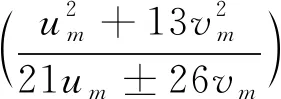
(16)

另外,由式(7)推出

所以

(17)

当8|m时,由式(9)得21um±26vm≡4(mod 17),因此

(18)

由式(16)～(18),引理2得证。

利用与引理2类似的证明过程,可以得到引理3，证明过程略去。

引理3∀m∈N+,有

(19)

引理4当n≥0时,若26(xn+21)是完全平方数,则n≡0,2(mod 1 200·7·13)。

证明为方便起见,令Hn=26(xn+21)。根据式(3)～(5)容易证明以下递推关系:

Hn+2=1 298Hn+1-Hn-707 616

H0=676,H1=206 596

假设对于非负整数n,Hn是完全平方数。下面的模素数p的运算是直接对数列{Hn}进行的,取最小非负剩余。证明分为4步进行。

第1步：证明n≡0,2(mod 1 200)。

1) mod 59,{Hn}的剩余类序列周期是4。因为n≡1,3(mod 4)分别对应着Hn≡37,52(mod 59),是非平方剩余,故排除。故余下n≡0,2(mod 4)等价于n≡0,2,4,6(mod 8)。

2) mod 7,{Hn}的剩余类序列周期是8。因为n≡4,6(mod 8)，对应着Hn≡3(mod 7)是非平方剩余,故排除。余下n≡0,2(mod 8)。

为简便起见,以下省略了关于剩余类序列周期的说明。

3) mod 61,排除n≡1(mod 5),因为Hn≡50(mod 61)是非平方剩余;mod 131,排除n≡3,4(mod 5),因为Hn≡116,47(mod 131)是非平方剩余。故，余下n≡0,2(mod 5 )。由于n≡0,2(mod 8),有n≡0,2,10,32(mod 40),等价于n≡0,2,10,32,40,42,50,72(mod 80)。

4) mod 19,排除n≡12(mod 20),因为Hn≡3(mod 19)是非平方剩余。故排除n≡32,72(mod 80),余下n≡0,2,10,40,42,50(mod 80)。

5) mod 239,排除n≡40(mod 80),因为Hn≡177(mod 239)是非平方剩余。故余下n≡0,2,10,42,50(mod 80),等价于n≡0,2,10,42,50,80,82,90,122,130,160,162,170,202,210(mod 240)。

6) mod 433,排除n≡1(mod 3),因为Hn≡55(mod 433)是非二次剩余。故排除n≡10,82,130,160,202(mod 240),余下n≡0,2,42,50,80,90,122,162,170,210(mod 240)。

7) mod 181,排除n≡12,20(mod 30),因为Hn≡104,54(mod 181)是非平方剩余。故排除n≡42,50,80,162,170(mod 240),余下n≡0,2,90,122,210(mod 240)。

8) mod 673,排除n≡10(mod 16),因为Hn≡668(mod 673)是非平方剩余。故排除n≡90,122(mod 240),余下n≡0,2,210(mod 240)。

9) mod 3 121,排除n≡10(mod 40),因为Hn≡2 162(mod 3 121)是非平方剩余,故排除n≡210(mod 240),余下n≡0,2(mod 240),等价于n≡0,2,240,242,480,482,720,722,960,962(mod 1 200)。

10) mod449,排除n≡30,32,60,90,92,120,122(mod 150),因为Hn≡109,402,151,15,284,432,17(mod 449)是非平方剩余。故排除n≡240, 242, 480, 482, 720, 722, 960(mod 1 200),余下n≡0,2,962(mod 1 200)。

11) mod 4 801,排除n≡162(mod 200),因为Hn≡2 508(mod 4 801)是非平方剩余。故排除n≡962(mod 1 200),余下n≡0,2(mod 1 200)。

第2步:证明n≡0,2(mod 7)。

1)mod 1 429,排除n≡1,6(mod 7),因为Hn≡820,390(mod 1 429)是非平方剩余。mod 29,排除n≡4,11(mod 14),因为Hn≡27,21(mod 29)是非平方剩余。故排除n≡4(mod 7),余下n≡0,2,3,5(mod 7)。注意前面已经证明了n≡0, 2(mod 1 200),故余下n≡0,2,1 200,1 202, 3 600,4 800,4 802,6 002(mod 8 400)。

2) mod 83,排除n≡12,26(mod 28),因为Hn≡50,46(mod 83)是非平方剩余。故排除n≡4 800,1 202(mod 8 400),余下n≡0,2,1 200,3 600,4 802,6 002(mod 8 400)。

3) mod 113,排除n≡10,16,24(mod 56),因为Hn≡76,24,23(mod 113)是非平方剩余。故排除n≡6 002,3 600,1 200(mod 8 400),余下n≡0,2,4 802(mod 8 400),即n≡0,2(mod 7)。

第3步:证明n≡0,2(mod 13)。

1) mod 53,排除n≡1,3,4,7,12(mod 13),因为Hn≡2,12,35,23,18(mod 53)是非平方剩余;mod 443,排除n≡8,9,11(mod 13),因为Hn≡228,60,353(mod 443)是非平方剩余。余下n≡0,2,5,6,10(mod 13),等价于n≡0,2,5,6,10,13,15,18,19,23(mod 26)。

2) mod 157,排除n≡5,10,13,15,18,19,23(mod 26),因为Hn≡85,65,102,65,150,85(mod 157)是非平方剩余,余下n≡0,2,6(mod 26)。又由于n≡0,2(mod 3),所以余下n≡0,2,6,26,32,54(mod 78)。

3) mod 1 873,排除n≡6,26,32(mod 39),因为Hn≡1 140,1 233,1 429(mod 1 873)是非平方剩余,故排除n≡6,26,32(mod 78),余下n≡0,2,54(mod 78),即n≡0,2(mod 13)。

第4步:证明n≡0,2(mod 1 200·7·13)。

从前面3步推出n≡0,2,8 400,38 402,46 802,62 400,70 800,100 802(mod 1 200·7·13)。

1) mod 127,排除n≡9(mod 21),因为Hn≡105(mod 127)是非平方剩余。故排除n≡62 400,70 800(mod 1 200·7·13),余下

n≡0,2,8 400,38 402,46 802,100 802(mod 1 200·7·13)

2) mod 337,排除n≡42(mod 56),因为Hn≡134(mod 337)是非平方剩余。故排除n≡38 402,46 802(mod 1 200·7·13)。余下n≡0,2,8 400,100 802(mod 1 200·7·13)。

3) mod 521,排除n≡80(mod 260),因为Hn≡272(mod 521)是非平方剩余。故排除n≡8 400(mod 1 200·7·13),余下n≡0,2,100 802(mod 1 200·7·13)。

4) mod 547,排除n≡65(mod 91),因为Hn≡163(mod 547)是非平方剩余。故排除n≡100 802(mod 1 200·7·13),余下n≡0,2(mod 1 200·7·13)。

综上,引理4得证。

引理5当n≥0时,若26(zn+21)是完全平方数,则n≡0(mod 180)。

证明证明过程与引理4类似。令Gn=26(zn+21),根据式(3)～(5)可得递推关系式

Gn+2=1 298Gn+1-Gn-707 616,

G0=0,G1=11 232

下面的模素数p的运算是对数列{Gn}进行的,取最小非负剩余。假设对某些n∈N,Gn是完全平方数。

1) mod 5,排除n≡1(mod 2),因为Gn≡2(mod 5)是非平方剩余。余下n≡0(mod 2),等价于n≡0,2(mod 4)。

2) mod 59,排除n≡2(mod 4),因为Gn≡30(mod 59)是非平方剩余。余下n≡0(mod 4),等价于n≡0,4,8,12,16(mod 20)。

3) mod 61,排除n≡1,2,4(mod 5),因为Gn≡8,59,37(mod 61)是非平方剩余。故排除n≡4,12,16(mod 20),余下n≡0,8(mod 20)。

4) mod 211,排除n≡3(mod 5),因为Gn≡162(mod 211)是非平方剩余。故排除n≡8(mod 20),余下n≡0(mod 20),即余下n≡0,20,40(mod 60)。

5) mod 89,排除n≡20(mod 30),因为Gn≡58(mod 89)是非平方剩余。故排除n≡20(mod 60),余下n≡0,40(mod 60)。

6) mod 181,排除n≡10(mod 30),因为Gn≡109(mod 181)是非平方剩余。故排除n≡40(mod 60),余下n≡0(mod 60),即n≡0,60,120(mod 180)。

7) mod 919,排除n≡3,6(mod 9),因为Gn≡51,668(mod 919)是非平方剩余。故排除n≡60,120(mod 180),余下n≡0(mod 180)。

引理5得证。

引理6若n≥0且n≡0(mod 1 200·7·13),则仅当n=0时,26(xn+21)是完全平方数。

证明根据式(3)～(5),当n=0时26(xn+21)=262。 若n>0,不妨设

n=2·2t·3·52·7·13·k,t≥3, 2⫮k

1) 当k≡1(mod 4)时,令

可得m≡2,4,12(mod 14),由此知21um+26vm≡25,23,5(mod 29),因此

(20)

另外,由式(14)推出xn≡x2m(modu2m),而由式(3)可知，x2m≡26v2m(modu2m),因此，xn≡26v2m(modu2m)。利用式(7),(20)及引理2可得

(21)

2) 当k≡3(mod 4)时,令

则m≡2,10(mod 14),由此知21um-26vm≡5,23(mod 29),所以

(22)

由式(14)、(3)得xn≡-26v2m(modu2m)。 与式(21)类似,由式(7)、引理2及式(22)推出

(23)

显然由式(21)和式(23)可知，当n>0时,26(xn+21)不是完全平方数。引理6得证。

引理7若n>0且n≡2(mod 1 200·7·13),则仅当n=2时26(xn+21)是完全平方数。

证明若n=2,则26(xn+21)=16 3542。 当n>2时,设

n=2+2·2t·3·52·7·13·k,t≥3, 2⫮k

(24)

m的取值为

1)m=2t·3,若t≡1,2,3,5,6,8,9,12,15,17,20,23,24,25,27,29,30,32,34,35,36,40,43,44,45,46,49(mod 51);

2)m=2t,若t≡0,7,16,21,22,28,33,39,42,47,48,50,55,61,64,69,70,82,88,98,101(mod 102);

3)m=2t·52,若t≡4,10,11,13,14,26,38,58,62,65,67,77,79,89(mod 102);

4)m=2t·3·5,若t≡37,41,84,90,92,93(mod 102);

5)m=2t·3·52,若t≡72,73(mod 102);

6)m=2t·7,若t≡51,99(mod 102);

7)m=2t·13,若t≡18,19,31(mod 102)。

则式(24)可写成n=2+2mr,r是奇数。由式(13)可得xn≡-x2≡-10 286 645(modum),故根据式(7)推出

容易验证

因此当n>2时,26(xn+21)不是完全平方数。引理7得证。

引理8若n≥0且n≡0(mod 180),则仅当n=0时26(zn+21)是完全平方数。

证明若n=0, 则26(zn+21)=0。 如果n>0,设

n=2·2t·32·5·k,t≥1, 2⫮k

1) 当k≡1(mod 4)时,设

则m≡3,4,6,7,9,15,20,21,22,24(mod 25),相应地有7um+26vm≡1,68,97,71,88,9,52,76,20,65(mod 101)。因此,

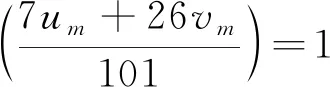
(25)

由式(3)及推论1得，zn≡z2m≡78v2m(modu2m)。再根据引理3、式(7)及式(25),可得

(26)

2) 当k≡3(mod 4)时,令

则m≡1,3,4,5,10,16,18,19,21,22(mod 25),相应地有7um-26vm≡65,20,76,52,9,88,71,97,68,1(mod 101)。因此

(27)

由式(3)及推论1，可得zn≡-z2m≡-78v2m(modu2m)。由此及引理3及式(7)、(27)推出

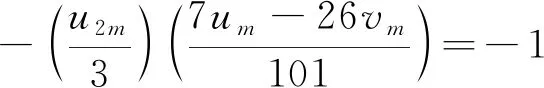
(28)

结合式(26)和式(28)可以得到，当n>0时26(zn+21)不是完全平方数。引理8得证。

2 定理的证明

因为y2=x3-30x+133=(x+7)(x2-7x+19),显然(x,y)=(-7,0)是方程(2)的一个解。因此,只需要考虑x>-7的情况。令d为x+7和x2-7x+19的最大公因数,那么d=1,3,9,13,39,117,且存在互素的正整数a,b使得

(29)

消去x可得

(2da2-21)2-d(2b)2=-27

(30)

当d=1时,由式(30)知(a,b)=(2,7),再由式(29)可得(x,y)=(-3,±14)；

当d=3时,由式(30)推出2a2-7≡0(mod 3),与a2≡0,1(mod 3)矛盾。

当d=9时,由式(30)得(2b)2-(6a2-7)2=3,解得a=b=1,因此(x,y)=(2,±9)；

当d=39时,由式(30)推出26a2-7≡0(mod 3),与a2≡0,1(mod 3)矛盾；

注意到,26a2-21≥-21。根据文献[23]的定理109,式(30)的全部解可写成下面的形式：

(31)

(32)

(33)

(34)

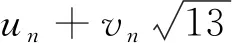
如果式(31)成立,那么

26a2-21=5un+26vn=xn

(35)

2b=2un+5vn

(36)

由式(35)知，26(xn+21)是完全平方数。根据引理4、引理6及引理7,有n=0,2,相应地得到(a,b)=(1, 1), (629,1 426 501)。再由式(27)可得(x,y)=(6,±13),(5 143 326,±11 664 498 677)

如果式(32)成立,则26a2-21=-5un+26vn。由式(5)和式(7)得到a2≡2(mod 3)。矛盾。

如果式(34)成立,那么26a2-21=-21un+78vn=zn,可得26(zn+21)是完全平方数。由引理5及引理8知n=0, 所以a=0。与a>0矛盾。

当d=117时,式(30)可化为

(78a2-7)2-13(2b)2=-3

(37)

(38)

或

(39)

式中：n为非负整数。

综上所述,定理1得证。

3 结 语

椭圆曲线的整数点问题一直是数论学者研究的热点问题。 由于曲线类型的多样性,没有一个统一的方法或算法能在有限步之内求解出任意给定的椭圆曲线的整数点。本文将椭圆曲线的整数点问题转化为研究递推序列的数论性质(主要是同余性质),并最终利用排除法求出了所有整数点。递推序列方法虽然是一种初等的方法,但通过与二次剩余相结合并运用一定的技巧,往往变得十分有力,能解决一些困难的丢番图方程求解问题。