构建数学模型 挖掘思维深度

高买花 徐甜甜

【摘 要】对最短路径问题的研究，可利用思维转换，将一个实际问题通过建立数学模型的方式，“转化”成数学几何问题;再结合相应的数学定理，进行合情推理、逻辑证明，解决这个数学问题;最后再将得到的结论“还原”至实际问题之中。在此实证过程中，教师作为引导者，需要给予学生及时、合理的指引，让学生通过不断的思考和练习，提升逻辑思维能力、推理论证能力和归纳总结能力。

【关键词】最短路径;化归;创新提高

古往今来，最短路径问题都是人们不断探索研究的经典问题，李颀的《古从军行》中“白日登山望烽火，黄昏饮马傍交河”就体现了这一问题。作为一名数学教师，笔者认为对最短路径问题的研究，可利用思维转换，将一个实际问题，通过建立数学模型的方式，“转化”成数学几何问题;再结合相应的数学定理，进行合情推理、逻辑证明，解决这个数学问题;最后再将得到的结论“还原”至实际问题之中。在此实证过程中，教师作为引导者，需要给予学生及时、合理的指引，让学生通过不断的思考和练习，提升逻辑思维能力、推理论证能力和归纳总结能力。本文将通过详细分析讲解数学教学中出现的最短路径问题，进行相应数学建模的探索。

一、联系“化归”思想，建立归纳模型

“化归”即转化归纳，由难化易，由繁化简。在中学数学的学习中，化归思想无处不在，在解决主要考查内容一致但形式多变的数学问题时，我们需要运用化归思想，将复杂多变的问题转化成熟悉一致的问题。通过多次练习熟悉了这些相似的数学问题之后，便可建立模型，进行归纳总结。

例如：

古希腊亚地山大里亚城有一位久负盛名的学者，名叫海伦。有一天，有位将军不远万里专程前来向海伦求教一个百思不得其解的问题：将军从营地回家，需横跨一条河流，请问在哪儿过河路径最短？（不考虑河流的宽度）

模型一：两点在同一直线异侧

请问：将军从营地回家，从哪里过河路程最短？理论依据是什么？

模型二：两点在一直线同侧 （著名的“将军饮马”问题）

请问：将军和营地在河流同侧，战马在回家途中渴了，问：将军在哪里饮马路程最短？

模型三：“两线一点”型的线段和的最小值问题

某中学举行文艺晚会，桌子摆成两直排（AO、BO相较于点O），AO桌面上摆满了橘子，BO桌面上摆满了糖果，站在P处的学生小明先拿橘子再拿糖果，然后到P处座位就坐，请你帮他设计一条行走路线，使其所走的总路程最短。

模型四：“兩点两线”型的线段和的最小值问题

有两条街道AO、BO相交于点O，街道AO卖水果，街道BO卖文具，同学C和同学D分别在街道前面的草坪上做游戏，同学C先去街道AO买水果，再去街道BO买文具，送给同学D，请问，同学C怎么走路程最短？

以上四个模型，均以生活实际问题为背景，需要我们将实际问题中的图形和数据进行处理，将此生活问题转化为几何问题，如“河流”“桌子”“街道”可以类比为直线、射线，或者线段，“人”可以类比为“点”，将情境中的物体具体化为几何图形以后，便可根据其特点，结合相应的知识或定理，进行模型的分类、归纳。

学会建立数学模型，可以帮助学生从千变万化的题目之中，找到题目的共性，运用“化归”思想，将不同的数学题目整理为相同的数学模型，提高学生的做题效率，逐步形成由繁化简的数学思维。

二、层层递进，提升建模能力

在学会基础的建模以后，学生对怎样建立数学模型已经有了相应的了解，在此基础之上，我们可以通过对题目类型和难度的筛选，设置相应的梯度，层层递进，提升学生的思维能力和建模能力。

模型一：题中出现一个动点

当题中只出现一个动点时，可作定点关于动点所在直线的对称点，利用两点之间线段最短，或三角形两边之和大于第三边求出最小值。

例：如图1，在正方形ABCD中，点E为BC上一定点，BE=10，CE=14，P为BD上一动点，求PE+PC的最小值。

模型二：题中出现两个动点

当题中出现两个定点和两个动点时，可作两次定点关于动点所在直线的对称点。利用两点之间线段最短求出最小值。

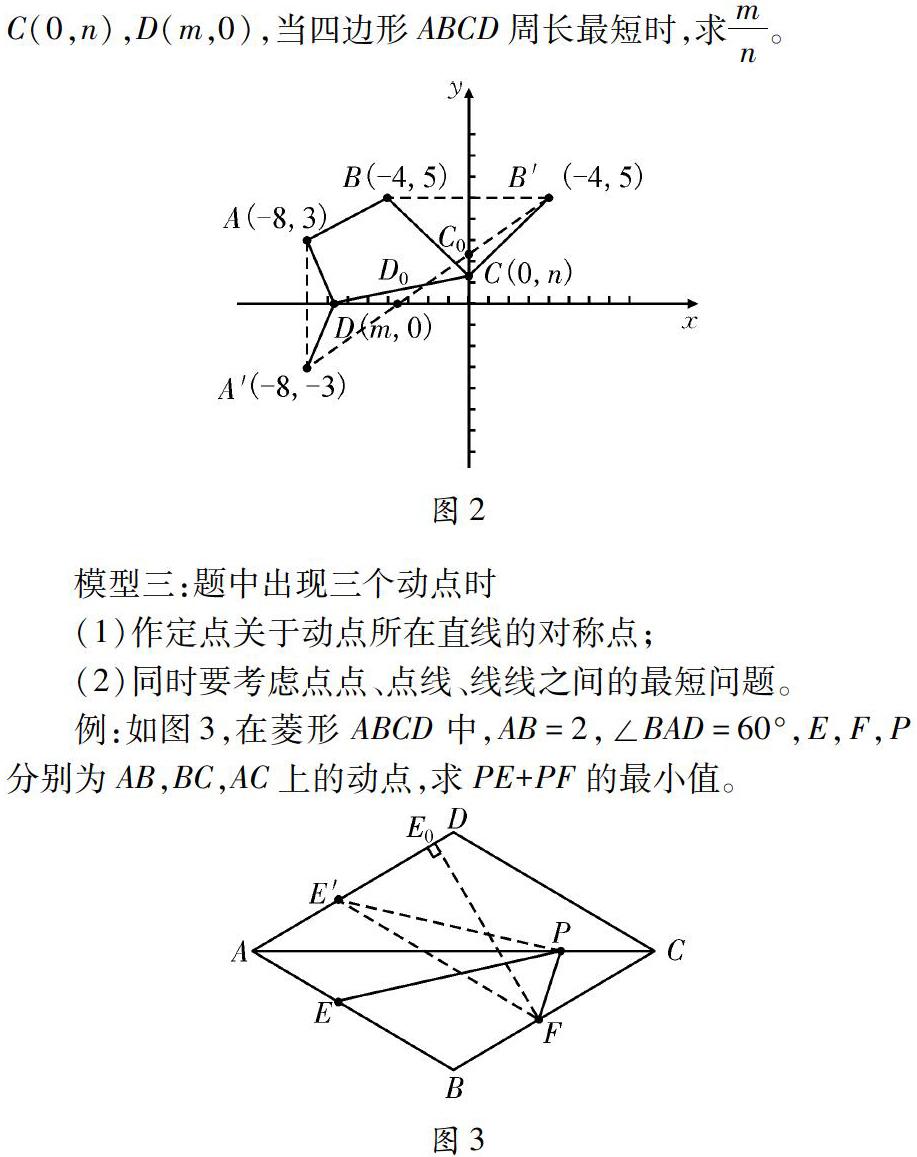
例：如图2，在直角坐标系中有四个点，A（-8，3），B（-4，5）C（0，n），D（m，0），当四边形ABCD周长最短时，求mn。

模型三：题中出现三个动点时

（1）作定点关于动点所在直线的对称点;

（2）同时要考虑点点、点线、线线之间的最短问题。

例：如图3，在菱形ABCD中，AB=2，∠BAD=60°，E，F，P分别为AB，BC，AC上的动点，求PE+PF的最小值。

三、创新提高，融汇建模思想

在数学教学中，教师除了向学生传授知识，并帮助他们学会归纳知识以外，更重要的是培养学生的创新思维和进取提高意识。我们可以通过一些新颖有趣的数学题，激发学生的思考探索意识，并从中获得突破自我的解题体验。在此过程中，学生不仅可以提升自己的思维能力，还能强化建模意识。

模型一：立体几何中的最短路径问题

桌上有一个圆柱形玻璃杯（无盖），高为12厘米，底面周长18厘米，在杯口内壁离杯口3厘米的A处有一滴蜜糖，一只小虫从桌上爬至杯子外壁，当它正好爬至蜜糖相对方向离桌面3厘米的B处时，突然发现了蜜糖，问小虫至少爬多少厘米才能到达蜜糖所在位置？

把圆柱展开，得到一个矩形，作点A关于矩形边长的对称点，最短距离就是线段的长，根据勾股定理解答即可。

模型二：二次函数中的最短路径问题

点D是抛物线y=-14x2+12x+154的顶点，点E在抛物线上，横坐标为4。M、N分别为 x轴、y轴上的动点，顺次连接D、N、M、E构成四边形DNME，求四边形DNME周长最小时点M和点N的坐标。

将最短路径问题和函数联系在一起，使得求两条线段之和转化为求三条线段之和，有助于培养学生的类比能力和创新能力。

四、结语

在初中数学的学习中，题目形式是多变的，但知识点和方法是相对固定的。在实际教学过程中，教师应有意识地帮助学生学会准确地在海量的题目之中分析出题目要考查的知识点，归纳相应的题目类型并建立正确的数学模型，运用“化归”思想，将题目清晰化、简单化;做到对从“题目由繁化简”到“快速准确建立数学模型”这一过程中学生可能出现的知识误区和盲点及时梳理，从而使学生能“由简入繁”地掌握“由繁到简”的学习方法，培养学生思维的广阔性、敏捷性、灵活性，实现“量”到“质”的飞跃，让不同学习能力的学生在不同的学习阶段都能学有所悟、学有所乐。

参考文献：

[1]王小莉.化归思想在中学数学教学中的渗透[J].教育现代化，2018（10）.

[2]魏玉琴.“最短路径”问题中化归思想的应用与策略[A].2019年中小学学素质创新研究大会，2019.

[3]尹加根.解析初中数学教学中的最短路径问题[J].数学学习与研究，2018（17）.

[4]张媛.关于初中数学最短路径问题的探究[J].高考，2017（06）.

[5]芦英峰.初中数学最短路径问题的探究与延伸[J].学苑教育，2016（10）.