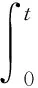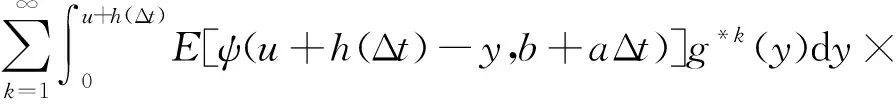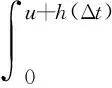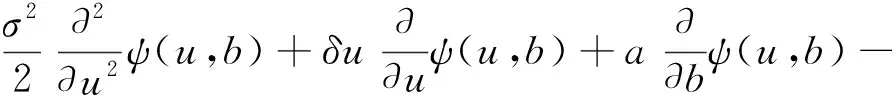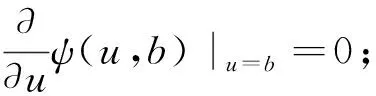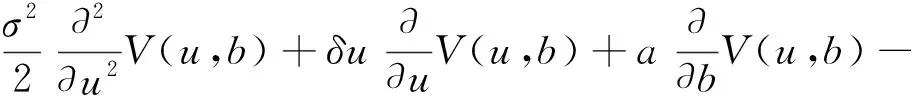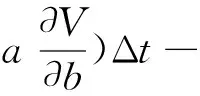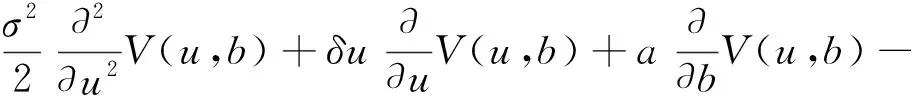线性红利下带干扰的复合Poisson-Geometric风险模型
2020-08-19侯致武乔克林
侯致武,乔克林
(1.延安大学西安创新学院 数据科学与工程学院,陕西 西安 710100;2.延安大学 数学与计算机科学学院,陕西 延安 716000)
0 引言
近年来,很多国内外学者基于经典的复合Poisson风险模型进行改进和完善。文献[1-5]在经典模型中引入利率因素、干扰因素、红利边界、随机保费等。但在保险业务的实际经营过程中,索赔次数并不完全服从Poisson分布,其方差往往会大于均值。文献[6-8]将经典风险模型进一步推广为更贴近实际的复合Poisson-Geometric风险模型,但保费收入是线性的。考虑到保费的随机性,文献[9-10]将复合Poisson-Geometric风险模型中的保费收入由线性函数推广为复合Poisson过程,但未考虑随机干扰因素。乔克林等[11]讨论了保费收入服从复合Poisson过程,理赔量服从复合Poisson-Geometric过程且带干扰的风险模型,但未考虑线性红利。侯致武等[12]建立了同时考虑利率因素、随机干扰因素、且保费收入为复合Poisson过程,索赔为复合Poisson-Geometric过程的风险模型,并给出了该模型的期望折现罚金函数所满足的积分微分方程。
考虑到保险公司实际经营的收益具有分红策略,本文建立了同时考虑利率因素、干扰因素、线性分红且保费收入为复合Poisson过程、索赔为复合Poisson-Geometric过程的风险模型,从而推广了文献[12]中的复合Poisson-Geometric风险模型,并且运用盈余过程的强马氏性和It公式,得到了保险公司的生存概率和红利付款的期望现值分别满足的积分微分方程。
1 预备知识
定义1 设文中所有随机变量都定义在完备概率空间(Ω,F,p)上,则常利力下带干扰的复合Poisson-Geometric风险模型为
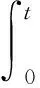
(1)
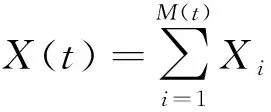
定义2 设线性红利界限为b+at(其中b为初值且u≤b,a为增长速率且0 (2) 定义3 记T=inf(t>0;U*(t)<0)(若集合为空集,则T=∞)为破产时刻,保险公司的最终破产概率φ(u,b)=P(T<∞|U*(0))=u),对应的生存概率为ψ(u,b)=1-φ(u,b)。 引理1[6]设N(t)是参数为(λ,ρ)的Poisson-Geometric过程,记α=λ(1-ρ)/ρ(若ρ=0,则α=λ),则当t足够小时,有 P{N(t)=0}=e-λt=1-λt+o(t), P{N(t)=k}=αρkt+Ak(t)ο(t),k=1,2,…, 记G*k(y)和g*k(y)分别为索赔分布G(y)和概率密度g(y)的k重卷积,并记 定理1 风险模型(2)的生存概率ψ(u,b)满足如下积分微分方程: 且满足边界条件: 1)事件B1:在(t,t+Δt)内,M(t)=0,N(t)=0,其发生的概率为 P(B1)=(1-λ1Δt+o(Δt))(1-λ2Δt+o(Δt))=1-(λ1+λ2)Δt+o(Δt)。 2)事件B2:在(t,t+Δt)内,M(t)=0,N(t)=k,其发生的概率为 P(B2)=(1-λ1Δt+o(Δt))[αρkΔt+Ak(Δt)o(Δt)]=αρkΔt+Ak(Δt)o(Δt)。 3)事件B3:在(t,t+Δt)内,M(t)=1,N(t)=0,其发生的概率为 P(B3)=λ1Δt(1-λ2Δt+o(Δt))=λ1Δt+o(Δt)。 4)事件B4:其他情况,其发生的概率为 P(B4)=o(Δt)。 当y>u+h(t)时,ψ(u+h(t)-y,b)=0,即破产必然发生。由盈余过程的强马氏性和全期望公式得 整理得 (λ1+λ2)ΔtE[ψ(u+h(Δt),b+aΔt)]=E[ψ(u+h(Δt),b+aΔt)]-ψ(u,b)+ (3) (λ1+λ2)ΔtE[ψ(u+h(Δt),b+aΔt)]=E[ψ(u+h(Δt),b+aΔt)]-ψ(u,b)+ (4) (5) 将(5)式代入(4)式后,两端同时除以Δt,令Δt→0,化简得 定理2 风险模型(2)下红利付款的期望现值V(u,b)满足积分微分方程: 并满足的边界条件: 证明当0≤u≤b时,类似于定理1的证明方法,由盈余过程的强马氏性和全期望公式得 V(u,b)=e-δΔtE[V(u+h(Δt),b+aΔt)]× [1-(λ1+λ2)Δt+o(Δt)]+ 由(5)式、引理1及单调收敛定理得 将eδΔt的Taylor展开式代入上式,等式两端同时除以Δt,令Δt→0,化简得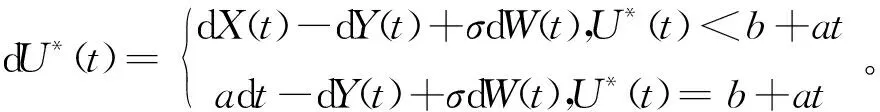
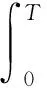
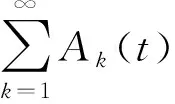
2 主要结果及证明