Lucas数列两项乘积倒数的有限和

张福玲

(渭南师范学院 数学与统计学院,陕西 渭南 714099)

0 引言

Lucas数列的递推公式为：

Ln=Ln-1+Ln-2，L0=2，L1=1，n≥2。

其通项公式为[1]：

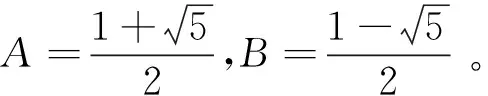
近年来许多学者对Lucas数列进行了一系列的研究，见文献[2-5]。文献[4]中给出了Lucas数列无限倒数和的等式：

文献[5-6]中给出了Lucas数列奇偶项平方的倒数和的等式：

通过Lucas数列的一些性质，得到了关于Lucas数列两项乘积倒数的有限和以及Lucas数列两项交错项乘积的倒数和的两个定理：

定理1对于任意的正整数n,m>1，有

定理2 对于任意的正整数n,m>1，有

1 主要引理

引理1[2]对于任意的正整数n,存在以下关系

引理2 设a,b,c,d为正整数，其中a+b=c+d，且b≥max{c,d}，得到

LaLb-LcLd=(-1)a+1Lb-cLb-d。

证明根据Lucas数列的通项公式有

LaLb-LcLd=(Aa-Ba)(Ab-Bb)-(Ac-Bc)(Ad-Bd)

=AcBd+AdBc-AaBb-AbBa

=(AB)a(Ac-aBd-a+Ad-aBc-a-Bb-a-Ab-a)

=(-1)a+1(Ab-a+Bb-a-Ac-aBb-c-Ab-cBc-a)

=(-1)a+1(Ac-a-Bc-a)(Ab-c-Bb-c)

=(-1)a+1Lb-cLb-d

根据引理2，令a=1,b=n+m+1,c=n+1,d=m+1可得

引理3 对于任意的正整数m和n，有

LmLn+Lm+1Ln+1=Lm+n+1。

根据引理2，令a=2,b=2n+2,c=d=n+2可得

引理4 对于任意的正整数n,有

根据引理3，令m=n-1,n=n可得

引理5 对于任意的正整数n，有

L2n=Ln-1Ln+LnLn+1。

引理6 对于任意的n≥1,那么

L2n+12+1>LnLn+1(Ln+12+1)。

所以

L2n+12+1>LnLn+1(Ln+12+1)。

引理7 对于任意的和n,有

证明根据引理2可得：

引理8 对于任意的m≥2和n,有

证明根据引理2可得

引理9 对于任意的n,有

证明根据引理2可得

引理10 对于任意的n≥1,有

证明根据引理2得

引理11 对于任意的n≥1,有

证明根据引理2、引理3和引理5可以得到：

引理12 对于任意的n≥1,有

证明根据引理2、引理3和引理5可以得到

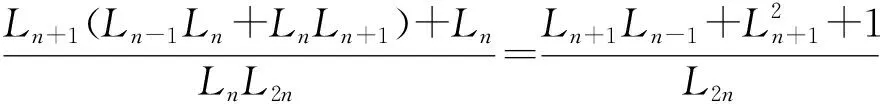
2 Lucas数列两项乘积的倒数和

定理1对于任意的正整数n，m>1，有

证明根据引理2可以得到

所以

从而可以得到

(1)

1)n为偶数时

所以

因此

(2)

对于任意的k,由引理1有

所以

从而

根据引理6

所以

(3)

由(2)和(3)

即当n为偶数时

(4)

2)n为奇数时

根据(1)可以得到

由于n为奇数，所以

根据引理4，

根据引理3

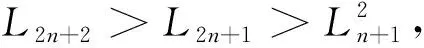
故

即

(5)

对于任意的k，根据引理1可以得到：

那么

所以

即

(6)

由(5)和(6)可以得到

即当n为奇数时，有

(7)

由(4)和(7)式可得定理1。

3 Lucas数列两项乘积交错项的倒数和

定理2 对于任意的正整数n，m>1，有

证明由引理2可以得到，当a=k,b=k+2，c=d=k+1时，

所以

因此

(8)

1)n为偶数时

由引理8和(8)可得

(9)

根据引理2

(10)

有

根据引理10，

即

从而可以得

(11)

根据引理11，

即

根据引理7

所以

即

(12)

结合(11)和(12)可得到

即当n为偶数时

(13)

2)n为奇数时

根据引理2、(9)和(10)

根据引理9

即

(14)

根据引理12

根据引理7

所以

即

(15)

结合(14)和(15)可以得到：

即，当n为奇数时

(16)

结合(13)和(16)可得定理2。