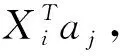矩阵剖析与PCA实例
2020-08-19万子峰蔡泽雄帅晨珊陈梦琪
万子峰,蔡泽雄,帅晨珊,陈梦琪
(南昌航空大学 a.信息工程学院; b.国际教育学院,南昌 330001)
1 矩阵变换

f(0,1)=(3,5,9)=3(1,0,0)+5(0,1,0)+9(0,0,1)
f(1,0)=(1,2,7)=1(1,0,0)+2(0,1,0)+7(0,0,1)
简而言之,B在f(A)上的投影为T(映射)。故有定义“矩阵表达的就是对线性运动的一种描述[1]”。
…
显然,旧基能线性表达新基且矩阵T为过渡矩阵。
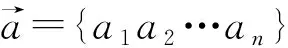
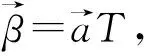
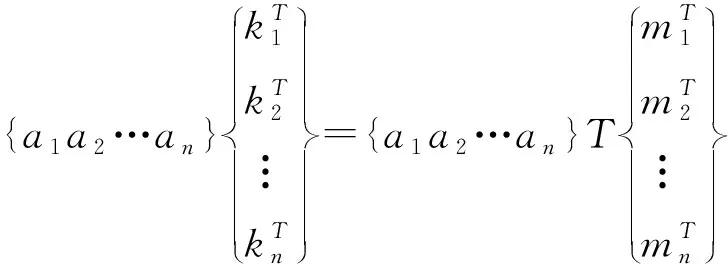
同时过渡矩阵T为满秩矩阵,是非奇异矩阵,由“非奇异矩阵行列式不为0”的性质可推T可逆得证。

图1 向量变换立体图Fig.1 Stereogram of vector transformation
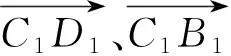
注意:原向量只能对应新向量在新坐标系中的所占权重,因为基之间并不能保证相互正交且长度为单位长度。
2 相似
教科书上对“相似”的定义:存在可逆矩阵p,使B=p-1Ap成立,那么说明A相似于B[2]。证明这个定义需要之前证明过的两个推理:


3.若第1条推理成立,则存在旧基坐标x与新基坐标y的转换关系y=T-1x,设有关系图表S,

图2 关系图表SFig.2 Relationship Chart S
通过图2,有:
①λ=T-1u(推理2)。
②λ=M2η(第2节的左乘推理)。
联立①②,得到③M2η=T-1u。
④由η=T-1j,两侧左乘T,得到Tη=j。
⑤u=M1j(左乘推理)。
联立③④,得到⑥M2T-1j=T-1u。
联立⑤⑥,得到⑦M2T-1j=T-1M1j。
⑦化简,得到结果M2=T-1M1T。
证毕。
所以相似矩阵也是一种对同一个线性运动在不同基的矩阵描述。纵使对矩阵进行了各种线性变化后,只要保证结果矩阵与原矩阵维持相似状态,则运动的本质就不会发生改变。
3 特征值与特征向量

AAT=U∑VT·V∑UT=U∑2U-1奇异值分解(SVD)定义:一个矩阵B可以分解成B=U∑VT,其中U的列向量两两正交且模为1,V列向量两两正交且模为1,即UT=U-1,VT=V-1,∑矩阵的主对角线为奇异值,其他元素为0。特征值是相对于方阵来说的,而奇异值分解则解除了这一限制,它适用于任意的矩阵。特征值与奇异值分解的关系:对任意矩阵A作svd,再对AAT作svd,AAT=U′∑V′T。又有U′=U,U-1=UT=V′T∴U′=V′=U,∑′=∑2。因此,对AAT作SVD,U′为其特征向量(为A中的U)。同理,对ATA作SVD,U′为其特征向量(为A中的V),∑′为特征值对角矩阵。
4 协方差矩阵
通常处理的数据都是多维的,“协方差”就是这样用来度量2个变量的关系,如果维数多于2,就用协方差矩阵。协方差定义:
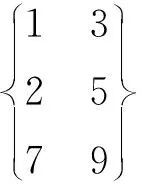
举例,假设有1组数据,用矩阵表示为:

根据协方差定义:
cov(x,y)=E[(1-E(x))(2-E(y))+(35-E(x))(25-E(y))+…]
cov(x,z)=E[(1-E(x))(3-E(z))+(35-E(x))(55-E(z))+…]
……
通过数据初始化,使E(x)=E(y)=E(z)=0,则X的协方差可表示为:
我们发现,对角线的元素就是各个变量的方差,即:

5 PCA过程