基于改进遗传算法的电子产品CTO订单推荐
2020-08-17韩海峰叶恒舟
韩海峰,叶恒舟,张 路
(桂林理工大学 广西嵌入式技术与智能系统重点实验室,广西 桂林 541006)
0 引 言
按订单配置(configure to order,CTO)起源于用户需求与偏好, 目标是快速、有效地满足用户的个性化需求,提升企业的核心竞争力。产品配置是实现CTO的关键,配置过程开展的前提是准确地获取客户需求。由于定制产品的复杂性不断提高,加上客户对产品结构、性能等认识不充分,往往仅能提出与自身体验和偏好相关的需求,因此具有模糊性和不确定性[1]。特别是对于电子产品,其物料清单(bill of material, BOM)往往包含数十项核心配件,每个配件有诸多品牌与型号可供选择,且产品更新较快,若采用过程式产品配置,需要用户对这些配置非常熟悉。在BOM选择过程中,难以满足全局性需求,也易忽略企业库存等影响因素。因此,有必要根据用户提出的局部和全局约束以及功能性需求,为客户推荐产品配置清单,帮助用户明确满足自身需求同时兼顾企业利益的CTO订单。
在需求获取方面,但斌等研究了一种需求智能获取方法,该方法关注用户表达需求的异质性,提供与用户的个人特征和使用情景相适应的需求表达方式,从而帮助用户提高需求描述的客观性和准确性[2]。Carulli等通过建立产品虚拟样机和虚拟现实环境,在早期帮助客户直观感知产品,以辅助用户与专业设计人员沟通[3]。
以客户需求与企业资源为驱动,研究产品配置模型及求解算法是一个研究热点。传统CTO产品平台仅能满足已知的客户需求,文献[4]提出面向订单设计(engineering-to-order, ETO)的配置方法,在维持个性化需求的同时增强了设计重用性,提升了产品配置的适应能力;文献[5]在CTO和ETO模型的基础上,基于适应性开放体系结构产品平台,以个性化自行车配置过程为例,提出了一种个性化分布式产品配置过程;文献[6]基于ETO,从产品系列、产品部件、产品细节3个层面关注产品配置的价格与利润关联;文献[7]考虑了订单的紧急程度,以综合收益最大化为目标,将产品配置方案建模为一个多目标优化问题,并采用蚁群优化算法求解,该方法认为订单已经存在, 关注的是大规模个性化订单的整体调度问题;文献[8]探讨了多情境及需求的不确定性情况下大规模定制订单的优化配置问题。考虑到为用户定制一些复杂产品繁琐费时,文献[9]在产品配置过程中,采用基于基尼指数的问答导航属性选择策略,帮助设计人员更好地获取用户需求与偏好;文献[10]讨论了云制造环境下个性化产品配置,重点是基于关联规则挖掘的产品初步配置以及基于蚁群算法的产品完整配置;文献[11]在产品配置时重点关注了用户的感性需求;文献[12]也根据用户需求为用户推荐产品配置结果,将其应用到多功能液压千斤顶的配置设计,但它强调的是规则匹配,而所采用的交互式遗传算法需要用户来评价种群个体适应度,交互过程复杂冗长。
综上可知,现有关于CTO产品配置的研究大多是考虑如何在用户个性化需求及生产成本的基础上,将大量的CTO订单进行整合获取BOM,而忽略了CTO订单本身如何根据用户的个性化需求而明确化。针对这一问题,本文根据用户的个性化需求描述,通过一种半交互过程帮助用户高效确定CTO订单,其核心是构建一个针对电子产品的CTO订单推荐(CTO order recommendation, CTOR)模型, 并采用一种支持自适应多样性维护特性的改进遗传算法(adaptive diversity maintenance of genetic algorithms, ADM-GA)求解该模型。
1 电子产品CTOR模型
设某电子产品的BOM包含n个配件,每个配件有若干个品牌,每个品牌有若干个型号可供选择。CTO订单推荐就是要为每个配件选择某个品牌下的某个型号,以满足用户的个性化需求,并兼顾企业库存等信息。
用户的个性化需求可以归结为3类:1)功能定位性需求,如定位为商务型; 2)针对配件或可分解为针对配件的局部需求, 如内存不小于4 G、 CPU是Intel、 配色为银白等; 3)针对全部或多个配件的全局约束,如对价格、 功耗、 重量等的要求。 由于第2类的局部需求只需要对各个配件的候选集作筛选, 而企业库存则可以通过调整配件价格来体现(如对于库存中没有的配件适当提高价格),因此,要满足用户的个性化需求,可以考虑以功能定位目标贴近度为优化目标,价格及功耗等为约束条件构建配件清单推荐模型,并通过求解该模型为用户推荐满足其个性化需求的订单。
1.1 功能定位目标贴近度
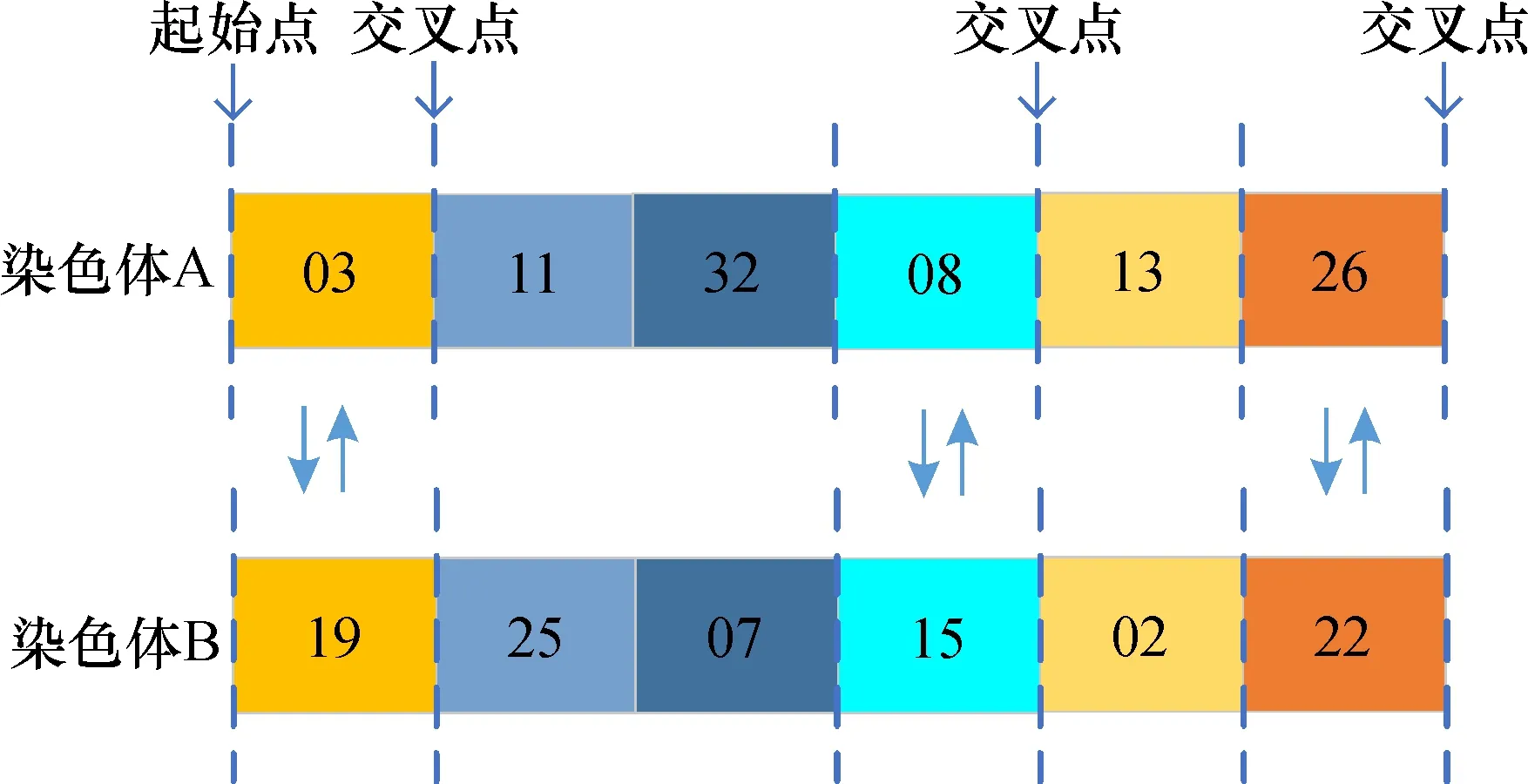
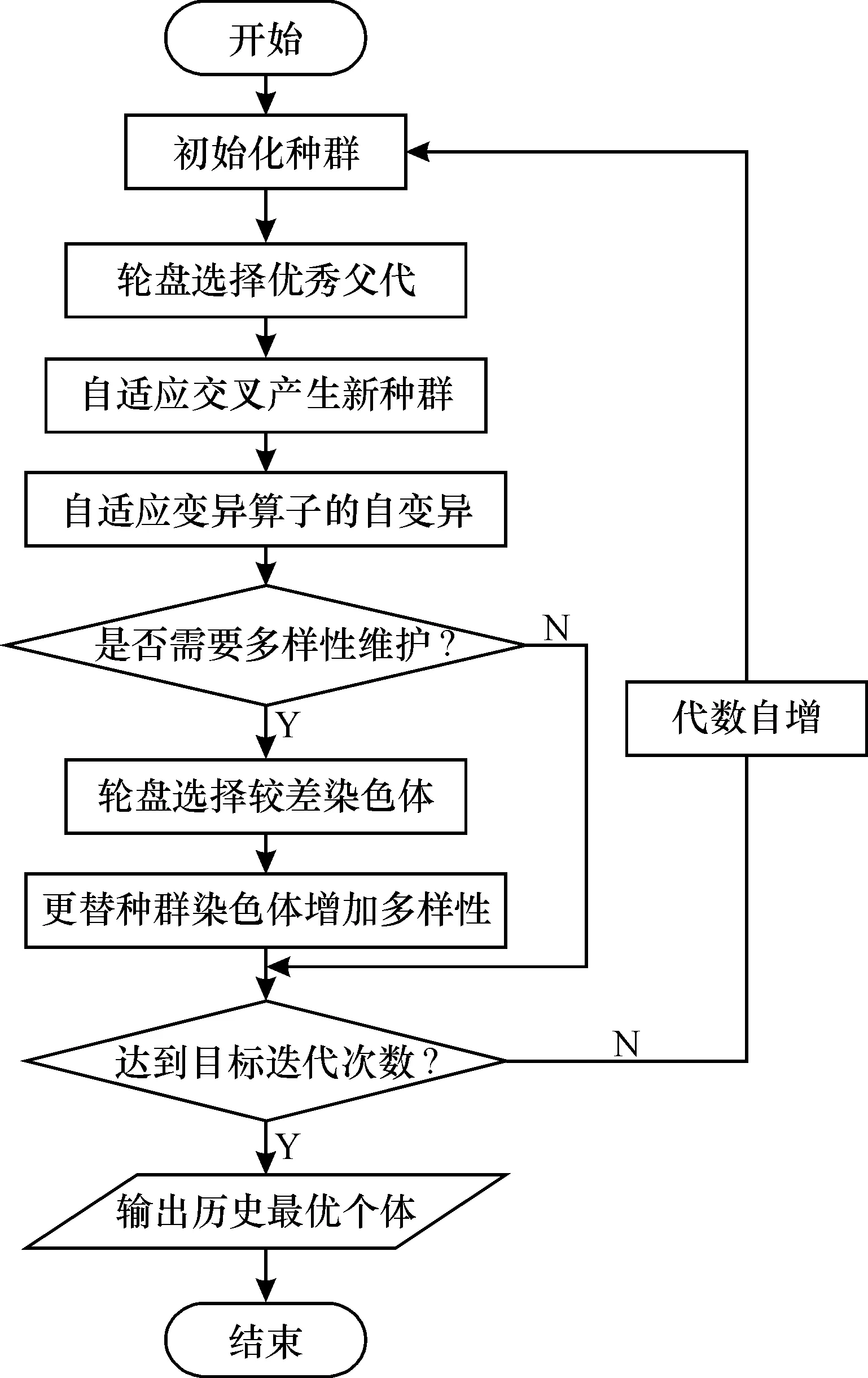
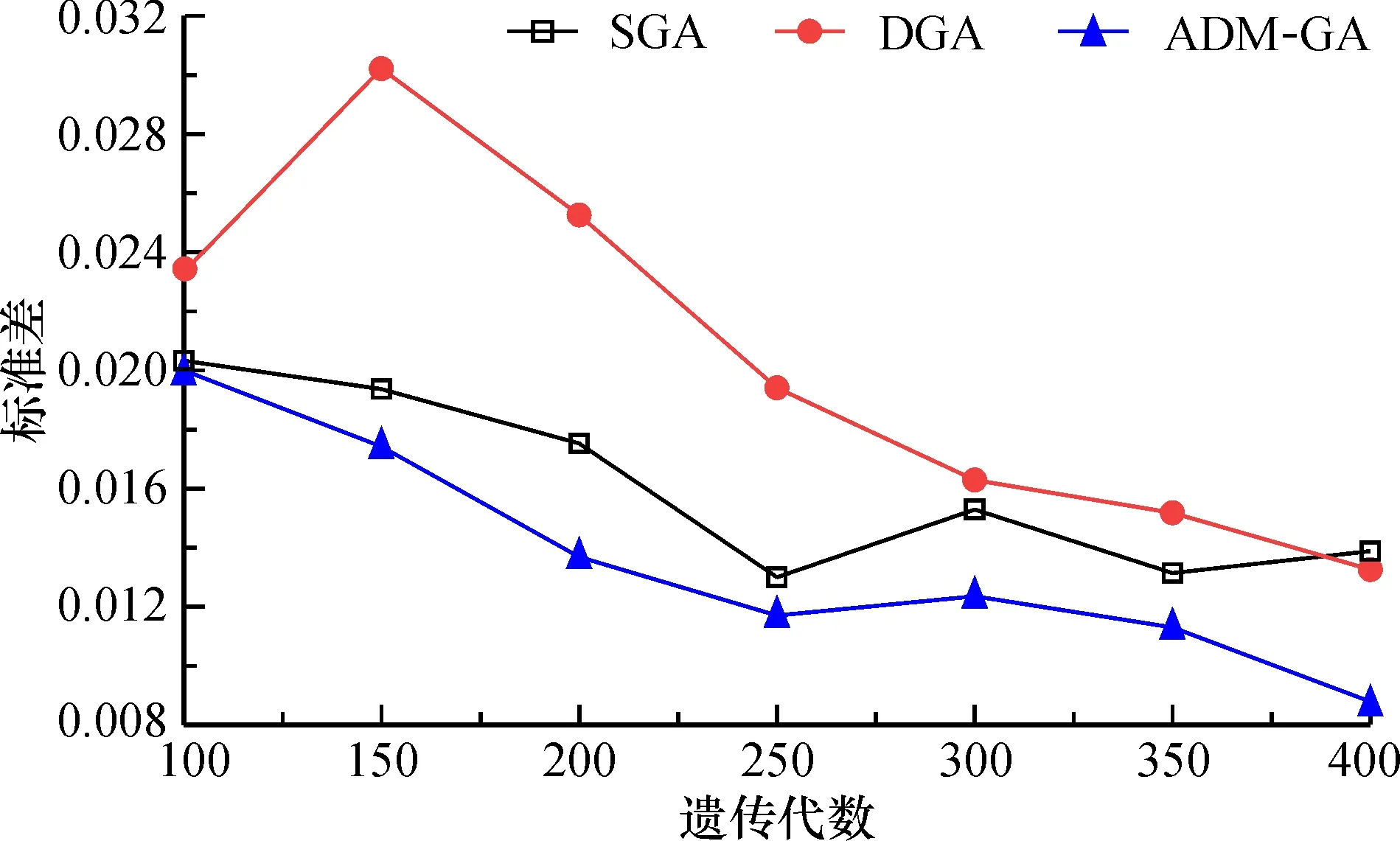
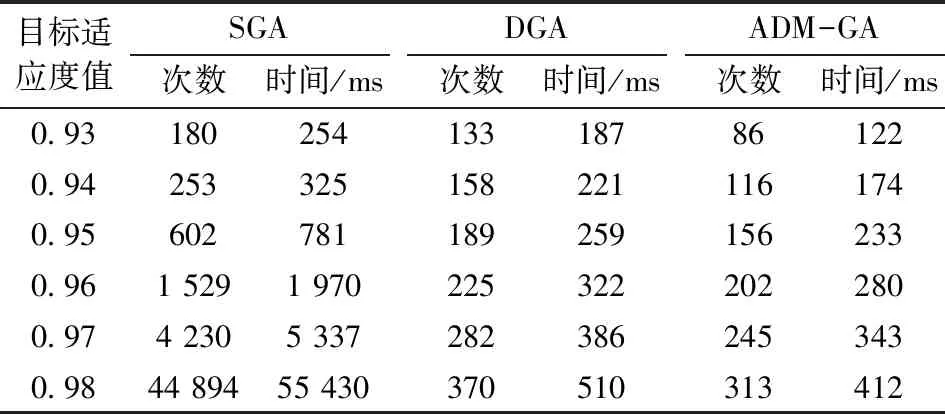
假设描述某种功能定位涉及r1,r2, …,ru等u个指标, 指标ri(i=1, 2, …,u)的既定目标属于{ai, …,bi}。 设指标ri的可选集CSi={vi1,vi2, …,vid}, 即该指标可以有d个不同的选择值(或区间), 而用户为该指标选择值(或区间)为vi, 记集合SSi={v|v∈CSi∧((vi≤v∧v (1) 其中, |SSi|、 |CSi|分别表示集合SSi、CSi中元素的个数。 例如, 设商务手机的标准GPU型号定位在集合{530, 540}中, 而GPU型号可选集为{430, 530, 540, 630, 640}。 若用户选择的型号为430, 则SS集为{430}, GPU功能定位目标贴近度为1-1/5=0.8; 若用户选择为530, 则SS集为空, GPU功能定位目标贴近度为1; 若用户选择640, 则SS集为{630, 640}, GPU功能定位目标贴近度为1-2/5=0.6。 总体的功能定位目标贴近度μ为 (2) 设某电子产品的选配清单涉及n个配件, 第i个配件有pi种选择(每种选择对应某个品牌下的某个型号),xij(i=1, 2, …,n;j=1, 2, …,pi)为0-1变量,xij=1表示第i个配件作出第j种选择, 则可以将该电子产品的CTOR模型构建为如下的多维多选择背包问题(multidimensional multiple-choice knapsack problem, MMKP)[13]: 目标:maxμ 约束条件: (3) (4) vr=fr(xij),r=r1,r2,…,ru; (5) (6) xij∈{0,1},i=1,2,…,n;j=1,2,…,pi。 (7) 其中, 式(3)描述价格约束,prij为第i个配件的第j种选择的价格,pr0为加工等成本, 认为是一个常数, [prcl,prcu]为用户约定的产品价格区间; 式(4)描述功耗约束,pcij为第i个配件的第j种选择的配件功耗(有些配件的功耗很小, 可以忽略不计, 即取值为0),pcc为用户约定的产品功耗上限; 式(5)描述根据用户的选择计算功能定位中某种指标值的方法。 CTOR模型是一个MMKP问题,诸如蚁群算法[14]、粒子群优化算法[15]等进化算法可以有效求解这类问题。其中遗传算法[16-17]具有分布式的全局搜索能力,对于多维组合优化问题具有良好的应用前景,不足在于收敛速度较慢以及存在局部收敛问题,通过调整遗传算子、构建多样性维护策略可以改善上述问题。 简单遗传算法(simple genetic algorithm, SGA)主要涉及编码、 设定初始种群、 适应度函数、 种群遗传操作(选择、 交叉、 变异)等核心要素。 种群个体采用实数编码方式。 染色体中的每个基因位对应一种配件, 基因的编码值代表该配件的选项序号(按照价格参数排序)。 种群的初始化随机产生, 仅保留满足约束条件的个体, 初始化种群个体的数量为N。 个体的适应度由功能定位目标贴近度确定。 种群选择采用回放式等概率采样的方式, 即轮盘赌。 第i个个体被选中的概率为 (8) 其中,fi(t)为第i个个体的适应度。 SGA中交叉变异最主要的两点:概率和方式。种群的交叉、变异概率为固定值(pc、pm)。交叉和变异方式均采用多点形式。多点交叉中,每个基因座的交叉起始点设在编码的起始(上一个基因座的末尾),交叉结束点在该基因座编码的末尾,每个个体的基因座都以概率pc发生交叉行为。变异方式类似交叉。 以实数编码为例, 染色体A的基因编码为[03 11 32 08 13 26], 染色体B的编码为[19 25 07 15 02 22], 发生交叉互换的位置分别发生在基因座1、 4、 6上, 那么交叉过后的新染色体A编码为[19 11 32 15 13 22], 新染色体B编码为[03 25 07 08 02 26], 如图1所示。 多点变异类似于多点交叉,若图1中染色体A的基因座1、 4、 6发生变异,则新染色体A的编码为[**11 32 **13 ** ], ** 为从相对应的基因座编码空间中随机选取的编码。 图1 染色体交叉Fig.1 Chromosome crossings 在SGA中, 遗传算子(选择算子、 交叉算子、 变异算子)是影响算法收敛速度的重要因素, 本文主要在交叉算子、 变异算子上采用自适应变化策略。 2.2.1 交叉算子设计 在SGA中,任意两个父代染色体的交叉变异概率是相同且固定的。如果采用差异化的交叉变异概率,即父代染色体的适应度越高,它们交叉变异的概率越低,有望使得适应度高的染色体更多地保留在下一代种群中,从而提高新种群的总体适应度。另一方面,对于适应度较低的染色体,在迭代前期的交叉变异概率应比迭代后期大;而对于适应度较高的染色体,在迭代前期的交叉变异概率应比迭代后期小。如此,在迭代前期可以扩大搜索范围,提升种群多样性,以避免早收敛;而在迭代后期,可以避免破坏种群收敛,提升寻优效果。基于以上理念,以种群的适应度均值为参照,设计了确定交叉算子的计算式: (9) 2.2.2 自变异算子设计 类似于交叉算子的设计理念,由第i个染色体的自变异概率为 (10) 其中,pm为标准遗传的变异概率;γ为可调系数。 遗传算法中的多样性可从染色体或基因多样性角度考虑。维持种群多样性是降低种群陷入局部最优的有效策略[18-19]。为避免破坏其收敛,每隔10代进行一次种群多样性检测,并根据检测结果判定是否进行维护。 第t代种群的多样性D(t)可度量为 (11) 其中,di(t)表示t代中所有个体的第i位上的等位基因出现频率最多的基因的次数;N为种群中染色体的个数;l为染色体的基因串的长度。 这种度量方式是从基因多样性的角度测量种群多样性。假设存在种群矩阵 (12) 矩阵中的每一行代表一个个体, 每一列代表相同基因座上的等位基因。 因为所有第1位等位基因中, 基因编码相同的最大数量是2(基因编码为3的数量最大), 故d1(t)=2; 类似可知,d2(t)=1、d3(t)=3、d4(t)=4。 由种群的多样性D(t)和g/step(g、step分别为当前迭代次数、 目标总迭代次数)共同确定种群更替占比ρ(表1)。 每次迭代后需要更新的个体数为ε·ρ·N(ε为可调参数)。 这些个体以一种新轮盘赌的方式选取, 并向种群中添加新生成的个体: 表1 种群更替占比ρ的确定Table 1 Determination of population replacement percentage ρ (13) 式中,pk(t)表示t代种群中第k个染色体的中间概率;fk(t)表示t代种群中第k个染色体的适应度;fbest(t)表示t代种群中最佳的个体适应度。然后,利用中间概率作为染色体被选中的概率,进行轮盘赌选择。 为了快速有效地求解CTOR模型,针对SGA收敛速度慢、收敛精度不足等缺点,进行了以下改进:①采用2.2节的方法设计自适应交叉算子与自变异算子,以提升遗传进化速度;②采用2.3节的方法加入种群多样性检测与维护机制,以保持种群多样性,缓解局部收敛问题。图 2为ADM-GA求解CTOR模型的流程。 图2 ADM-GA算法求解CTOR模型流程Fig.2 Solving CTOR model process with ADM-GA algorithm 实验PC机主要配置为:Intel(R)Core(TM)i7-9750H、2.6 GHz CPU、16 GB内存,64位Windows 10操作系统,编程语言为Java 1.7。实验时,考虑PC机的个性化订单问题。从公开的网络平台爬取了涉及显示器、CPU、GPU、主板、内存、硬盘、电源、键盘、鼠标、耳机等10个配件共计约348条记录,其中单个配件的最小记录条数为23条,最高为52条。 经过多次参数调节和统计数据发现,采用如表2所示的参数设置时,实验效果最佳。 表2 最佳参数设置组合Table 2 Parameter settings 实验对比了标准遗传算法(SGA)、在SGA的基础上添加2.2节设计的自适应遗传算子后的遗传算法(DGA)、本文算法(在DGA的基础上加入2.3节多样性检测与维护策略后的遗传算法, 记为ADM-GA)3种算法的性能。 为提升实验数据的可靠性, 实验结果为测试50次后的各相关指标数值(适应度、 遗传代数、 迭代时间)的均值或标准差。 图3对比了各代种群的历史最佳适应度。 可见,3种算法在迭代前期(<200代)都能较快地趋近最优解, 200代之后逐渐缓慢。 在到达相同的迭代次数时, ADM-GA比SGA和DGA可以获得更好的适应度。 图3 3种算法的历史最佳适应度值Fig.3 Historical optimal fitness values of the three algorithms 图4对比了3种算法所获得的最佳适应度的标准差。可见,标准差越小, 稳定性越好。 3种算法的稳定性总体上为: ADM-GA>SGA>DGA。 DGA的稳定性弱于SGA, 是因为引入自适应交叉和自变异算子后, 虽然在收敛速度上有所加快, 但更容易陷于局部收敛; 而ADM-GA在DGA的基础上, 加入了多样性检测与恢复机制, 较好地克服了局部收敛问题, 稳定性较好。 图4 3种算法的适应度标准差Fig.4 Fitness standard deviation of the three algorithms 表3对比了3种算法达到相应的目标适应度值时所需要的遗传代数及时间开销。 其中, 时间开销仅统计了种群初始化、 选择、 交叉、 变异、 适应度计算、 多样性检测与维护等操作, 而没有统计编码解码的时间开销(因为该过程的时间开销较大, 且3种算法所花时间是相同的)。 可见,3种算法的时间开销均随着目标适应度的增加而增加, 但DGA与ADM-GA的增速比SGA缓慢很多; 达到同一目标适应度, ADM-GA所需要的迭代次数与时间开销均是最低的, DGA次之, SGA最高。 表3 3种算法迭代次数及时间开销Table 3 Iteration times and time cost of the three algorithms 确定电子产品的CTO订单是实现个性化设计与生产的重要基础,其目标是根据用户的个性化需求确定产品所涉及的每个配件的品牌与型号。CTO订单推荐可辅助用户与专业设计人员沟通,以快速、准确地确定CTO订单。通过形式化度量功能定位目标贴近度指标,电子产品CTO订单推荐被建模为一个多维多选择背包问题。为了克服经典遗传算法存在局部收敛及收敛速度较慢等不足,在用遗传算法求解该问题时,提出了新的遗传算子自适应调节方法及种群多样性检测与维护策略。当前的CTO订单推荐,仅从用户的角度进行了优化,同时从用户与生产商角度(如优先利用现有库存、 推荐和优化现有生产线加工产品等)进行优化,是下一阶段的研究方向。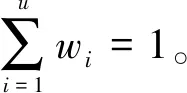
1.2 CTOR模型
2 改进遗传算法求解CTOR模型
2.1 简单遗传算法
2.2 自适应遗传算子设计
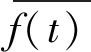
2.3 种群多样性检测与维护

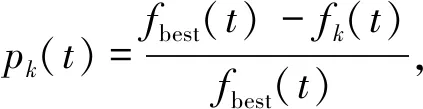
2.4 求解CTOR模型
3 实验仿真与分析
3.1 实验环境与参数取值

3.2 实验结果分析

4 结 论
