我国消费行业间风险度量及相依性研究

李世君,唐国强,杜诗雪

(桂林理工大学 理学院,广西 桂林 541006)

0 引 言

食品加工制造、饮料制造、服装家纺、白色家电、汽车整车等行业与人们的日常生活息息相关。随着市场需求的转变和国际竞争日趋激烈,食品行业产业结构亟待优化;饮料行业进入稳中有升时期,不再高速增长；服装行业内马太效应进一步加强,龙头强者恒强；白色家电行业结构趋于稳定；随着汽车的普及,全国汽车行业形成了可以满足不同消费层次需求的市场体系。对消费行业间风险度量及相依关系的研究有重要意义。

国内外学者对风险度量及相依性进行了大量研究： 孙红梅等[1]以欧洲金融危机为例, 采用GARCH模型与C-Vine Copula进行金融危机的传导效应研究； 韩超等[2]采用AR-GJR-GARCH模型结合广义帕累托分布, 通过蒙特卡罗方法计算组合风险价值(VaR), 运用高维动态C-Vine和D-Vine Copula对外汇对数收益率进行实证研究； 姚登宝等[3]采用ARMA(1,1)-GJR-GARCH(1,1)-Copula模型从市场流动性和市场预期两方面来分析动态相关结构；吴智昊[4]基于变结构Copula模型对股市和汇市之间的波动溢出效应进行研究； 许启发等[5]基于D-Vine Copula-分位数回归对能源市场3种期货商品和不同行业5只股票进行研究； 侯仲凯等[6]采用滚动时间窗衡量动态VaR, 构建混合R-Vine Copula模型对次贷危机、 欧洲债务危机前后行业市场传染效应进行研究； 余乐安等[7]通过R-Vine Copula研究不同行业数据来分析国际油价与中美股价的相依关系；孙国华等[8]选择恰当的Copula函数证明了两种期货收益率的下尾相关性强于上尾相关性；劳齐莹等[9]基于VAR-VEC模型对我国大宗商品价格指数与生产者价格指数进行研究,发现二者之间存在长期稳定的均衡关系；Goel等[10]利用SCAR C-Vine Copula分析金融危机时的市场传染效应;Bensaïda等[11]采用马尔可夫状态转换C-Vine和D-Vine分解学生tCopula研究G7股票市场;Song等[12]使用Vine Copula与因子Copula对金砖国家、G7国家、G20国家进行风险研究。

现有研究多是对大盘指数和个股进行研究, 对大盘市场的研究很难对普通投资者有直接的贡献,对个股研究又过于局限,很难给出一般性指导意见,基于此,本文站在普通投资者的角度,采用ARMA-GARCH偏t模型求取VaR与藤Copula模型结合对涉及“衣食住行”的五项行业进行研究。

1 理论模型介绍

1.1 ARMA(p,q)-GARCH(1,1)-偏t模型

ARMA(p,q)-GARCH(1,1)-偏t模型:

(1)

式中,rt为对数收益率；μ为均值；p为自回归阶数；q为移动平均阶数；at为残差项；σt为标准差；φi为自相关系数；θj为偏自相关系数；{εt}为独立同分布零均值白噪声序列；α0为截距项；α1为ARCH项；β1为GARCH项，α0>0,α1>0,β1>0, 0<α1+β1<1。

1.2 VaR的计算与检验

对数收益率序列在时刻t的观察值记为rt,在[t,t+h]期间的损失记为Lt+h=-(rt+h-rt)=Δr(h)。FL是损失函数的累积分布函数,记为FL(x)=P(L≤x)。VaR在显著性水平α(常取1%和5%)下的值实际上就是FL的α分位数，即VaR表示满足不等式FL(x)≥α的最小实数。

VaRα=inf(x|FL(x)≥α)。

(2)

多头交易头寸的情况下, 当交易资产价格下降时, 损失风险就会产生; 而在空头交易头寸的情况下, 资产价格上升时, 风险就会产生。 由于我国股市不允许做空机制, 所以仅考虑多头位置建模。

如果序列εt是具有偏t分布的随机变量, 自由度为ν, 那么条件分布的5%分位数是

VaR=μ+skstα,ν,εσ,

(3)

其中,skstα,ν,ε表示自由度为ν的偏t分布对应的0.05分位数的临界值。

假定计算VaR的显著性水平为α, 研究天数为T, 失败天数为N,N越接近T×α，表明效果越好。Kupiec[13]提出的检验为似然比检验

LR=2ln[(1-N/T)(T-N)(N/T)N]-

2ln[(1-p)(T-N)pN],

(4)

其中,LR统计量服从自由度为1的卡方分布, 用于检验实际失败率与设定的显著性水平是否相同, 依此检验模型的优劣。

1.3 C-Vine Copula与D-Vine Copula模型

Nelsen[14]将Copula定义为“将多元分布函数与其一元边际分布函数连接或耦合的函数”。 Copulas允许模拟具有不同特征的多种多变量分布,例如偏度、尾部依赖性等。在概率论方面,n维Copula定义为

C(u1,u2,…,un)=P(U1≤u1,U2≤u2,…,Un≤un),

(5)

其中,Ui(i=1,2,…,n)是定义在[0, 1]上的均匀分布。

Sklar定理: 令F(x1,x2,…,xn)表示变量x1,x2,…,xn的联合分布函数,其边际分布函数为F1(x1),F2(x2),…,Fn(xn), 则存在Copula函数C,使得

F(x1,x2,…,xn)=C[F1(x1),F2(x2),…,Fn(xn)]；

(6)

反之, 如果C是Copula函数,F1(x1),F2(x2),…,Fn(xn)是一元分布函数, 则F(x1,x2,…,xn)是一个联合分布函数, 边际分布函数为F1(x1),F2(x2),…,Fn(xn)。

为解决二元Copula函数存在的“维数诅咒”问题,开始研究高维Vine-Copula模型,其以pair Copula为组织框架,能够弥补二元Copula或多元Copula存在的诸多问题与不足,对多元变量之间的非线性相依关系进行灵活描述。

常规Vine分为C-Vine和D-Vine两种。C-Vine具有星形结构,使用根节点处的特定变量捕获变量之间的依赖性。在每个树中,通过选择根节点,并调节所有先前的根节点,相对于该节点建模形成所有节点的成对相依性。而D-Vine通过选择变量的预先特定顺序来构造。

C-Vine和D-Vine的概率密度分别为

(7)

和

(8)

其中，f(x1,x2,…,xn)为概率密度函数；fs(xs)为边缘密度函数；ci,i+j|i+1,…,i+j-1为Pair Copula密度函数。如5维C-Vine的一种密度函数为

c23|1×c24|1×c25|1×c34|12×c35|12×c45|123。

(9)

1.4 建模步骤

①获取行业收盘价数据,对收盘价序列进行取对数求差分处理,获得对数收益率序列。

②对五项行业对数收益率序列进行基本的描述性统计,自相关与偏自相关检验、正态性检验、平稳性检验、白噪声检验、ARCH效应检验,结果显示适合采用ARMA(p,q)-GARCH(1,1)偏t模型。

③对五项行业构建边缘分布,采用auto.arima()函数构建ARMA(p,q), 使其与GARCH(1,1)偏t模型相结合,模型很好地消除了自相关性与ARCH效应。

④通过对边缘分布产生的条件方差序列进行处理,求解VaR序列,并检验ARMA(p,q)-GARCH(1,1)偏t模型的风险度量效果。

⑤将VaR序列用经验累积分布函数进行转换。

⑥对转换后的VaR序列构建C-Vine Copula与D-Vine Copula模型。

2 风险度量研究

2.1 数据来源及预处理

选取食品加工制造(881134)、 饮料制造(881133)、 服装家纺(881136)、 白色家电(881131)、 汽车整车(881125)五项行业板块指数2007年8月1日—2019年6月20日的日收盘价作为研究样本, 共2 891个交易数据, 数据来源于同花顺客户端, 所选行业涉及“吃、 穿、 住、 行”。 采用日对数收益率进行分析, 日对数收益率定义为rt=lncpt-lncpt-1,cpt为第t日的收盘价,日对数收益率的数据量为2 890个。本文仅考虑多头位置建模。研究结果由R语言得出。

2.2 基本描述性统计

食品加工制造行业、饮料制造行业、服装家纺行业、白色家电行业、汽车整车行业等五项行业板块指数收盘价走势图如图1所示。可以看出,食品加工制造行业、服装家纺行业与白色家电行业(图1a、c、d)波动范围较为一致, 饮料制造行业与汽车整车行业(图1b、e)波动范围较为一致。

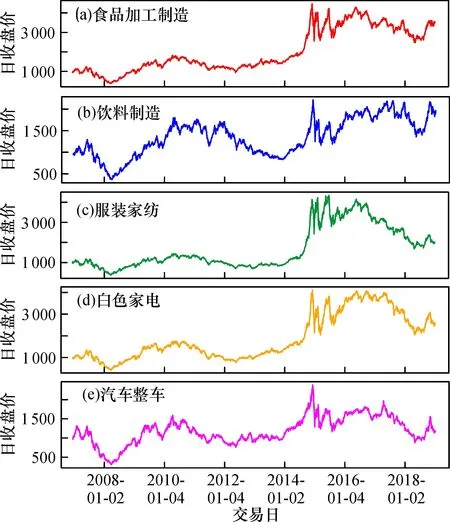
图1 五项行业板块指数收盘价走势图Fig.1 Closing price chart of five industry sector index

对五项行业指数收盘价数据作取对数求差分处理,绘制对数收益率时序图, 如图2所示。 可以看出,五项行业板块指数日对数收益率序列在0上下波动,波动范围大致是-0.10～0.10。存在波动聚集现象,即大幅波动后面是大幅波动,小幅波动后面是小幅波动。在2007与2015年期间存在大幅波动,对应于我国股市的牛市期间,牛熊转化过程中,振幅变大。

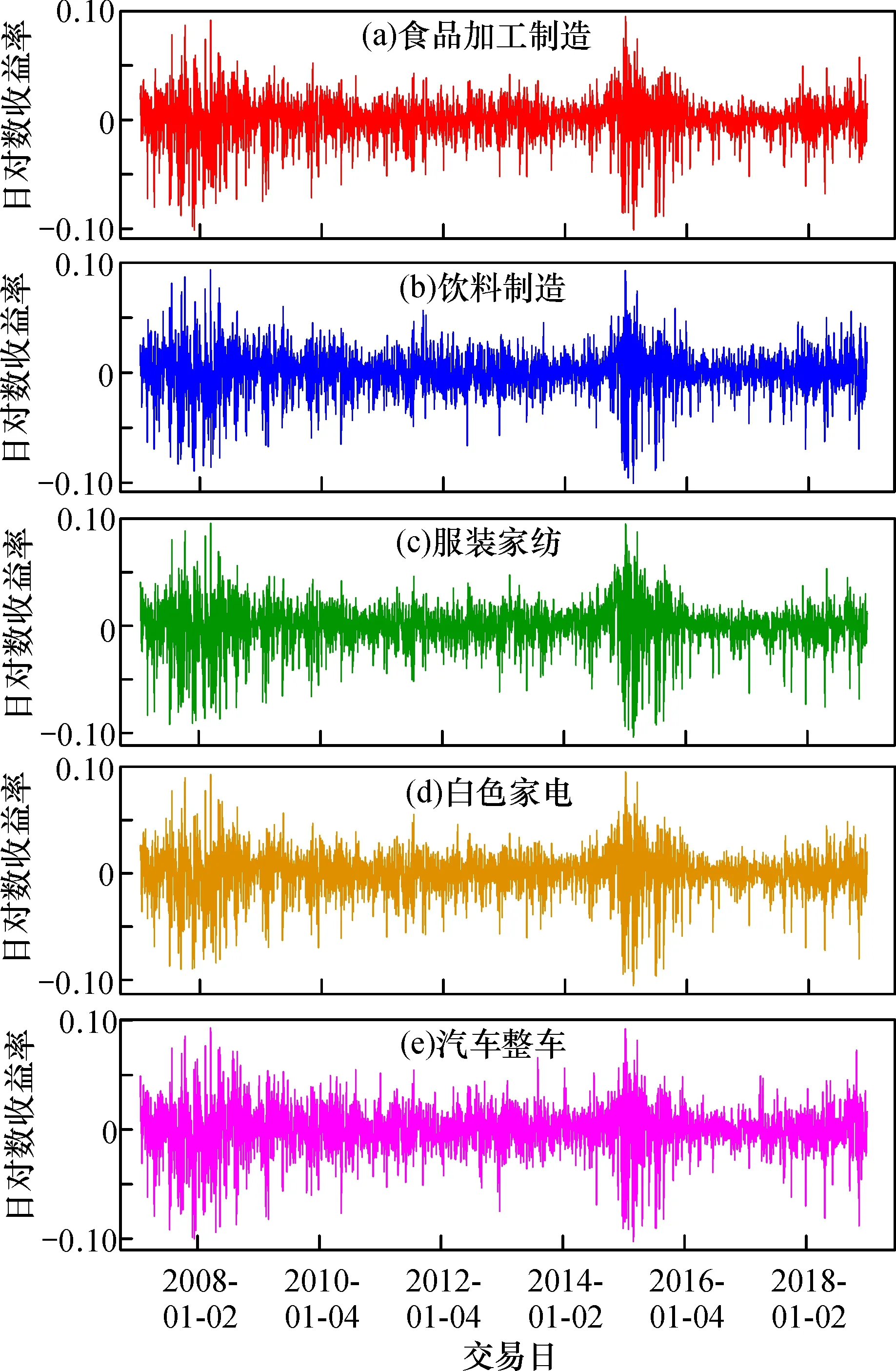
图2 五项行业板块指数日对数收益率时序图Fig.2 Timing chart of five industry sector index daily logarithmic yield

五项行业指数日对数收益率基本特征见表1,可知,五项行业指数日对数收益率均值均大于0,食品加工制造行业均值最大为0.000 460,汽车整车行业均值最小为0.000 070,偏度均小于0,峰度均大于3,呈现出左偏、尖峰厚尾特征。样本量为2 890,不存在缺失值,中位数均接近0,波动范围与通过图2观察所得一致。

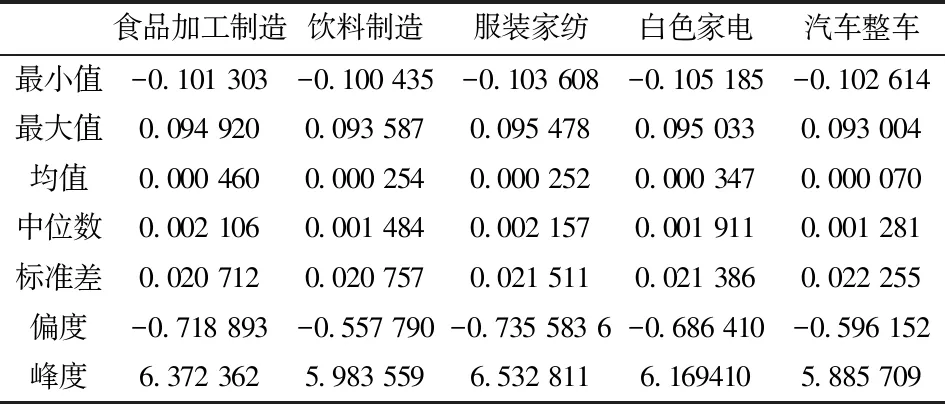
表1 五项行业指数日对数收益率基本特征Table 1 Basic characteristics of daily logarithmic yield of five industry indices

2.3 相关统计检验

由R语言绘出自相关与偏自相关图,如图3、图4所示,探讨食品加工制造行业、 饮料制造行业、服装家纺行业、白色家电行业、汽车整车行业对数收益率序列的自相关与偏自相关性。

由图3可知, 五项行业均存在自相关性; 由图4可知, 五项行业均存在偏自相关性。

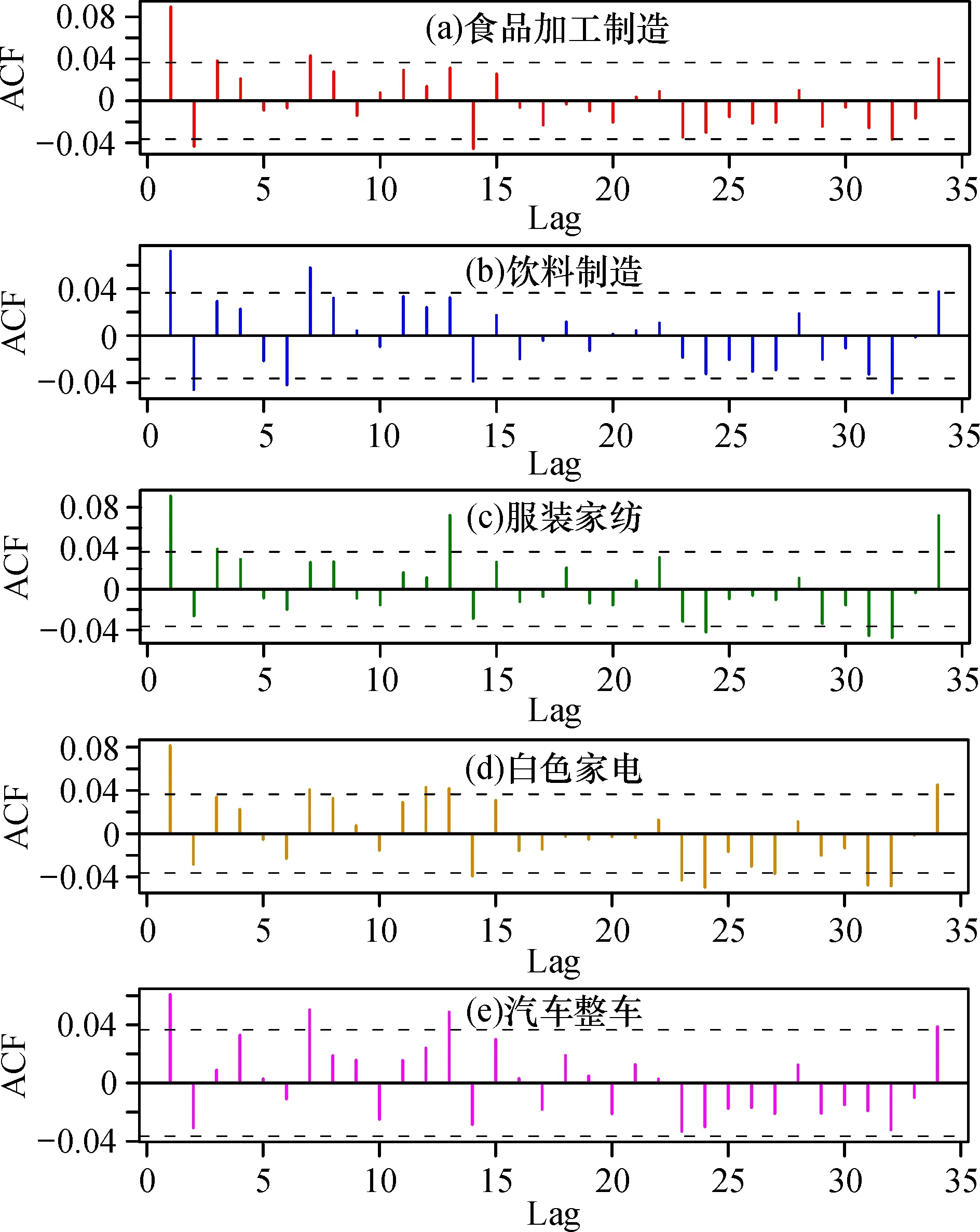
图3 五项行业板块指数日对数收益率自相关图Fig.3 Return autocorrelation chart of five-item sector index daily logarithmic rate

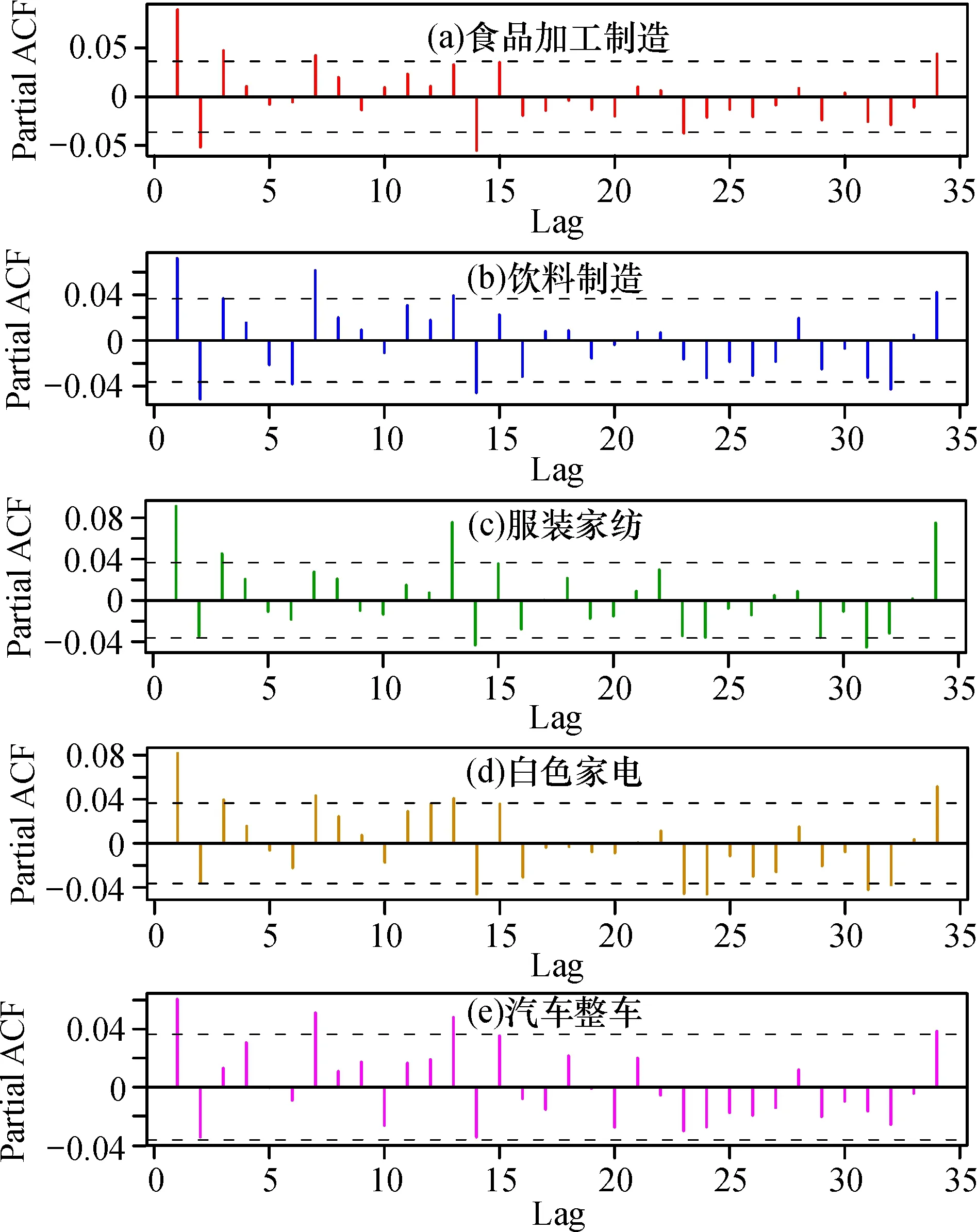
图4 五项行业板块指数日对数收益率偏自相关图Fig.4 Bias autocorrelation chart of five industry sector index daily logarithmic yield

对五项行业作基本的统计检验,结果见表2～4。由表2可知,正态性检验的p值均小于0.05,五项行业均拒绝对数收益率序列服从正态分布的原假设;由表3可知,平稳性检验与白噪声检验的p值均小于0.05,拒绝存在单位根和序列为白噪声的原假设;由表4可知,ARCH效应检验的p值均小于0.05,五项行业均存在ARCH效应。五项行业指数对数收益率均为平稳非正态非白噪声序列,具有ARCH效应。

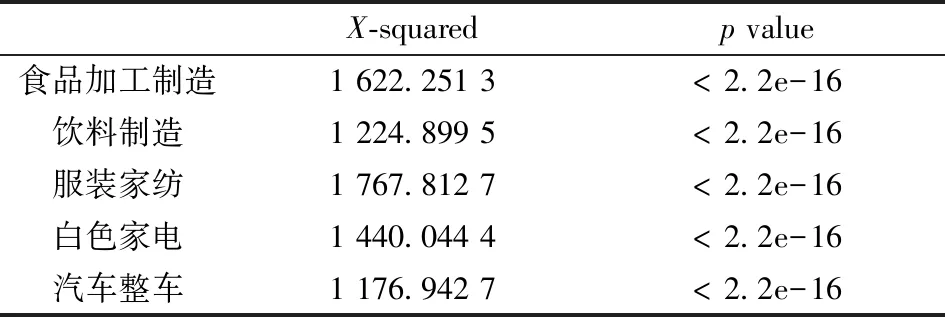
表2 Jarque-Bera正态性检验表Table 2 Jarque-Bera normality test

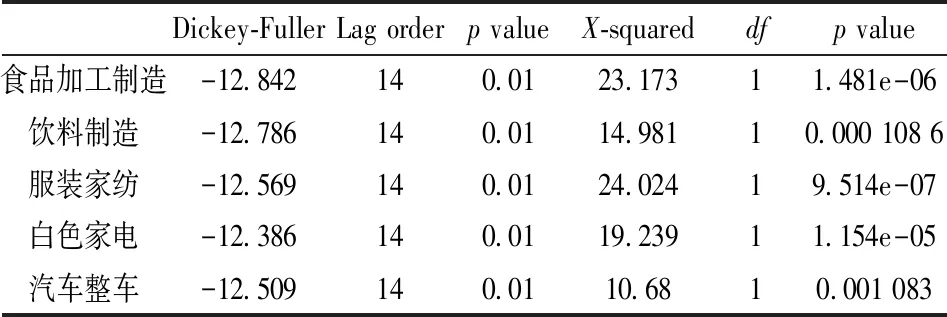
表3 平稳性检验与白噪声检验表Table 3 Stationarity test and white noise test

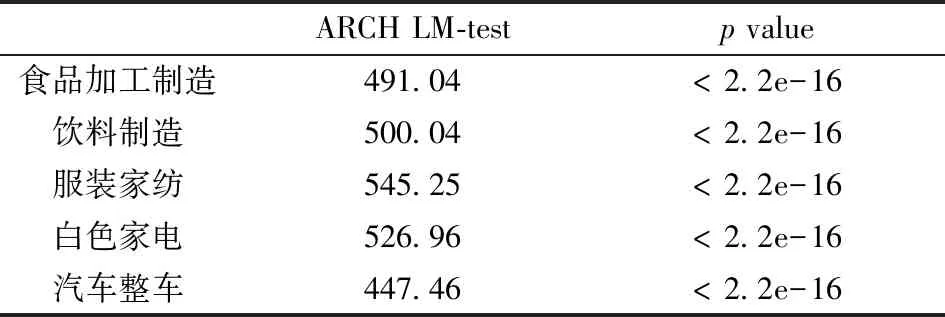
表4 ARCH效应检验表Table 4 ARCH effect check list

2.4 边缘分布构建

通过auto.arima()函数对五项行业自动选取ARMA(p,q)模型:食品加工制造行业选取ARMA(1,1),饮料制造行业选取ARMA(2, 3), 服装家纺行业选取ARMA(1,1),白色家电行业选取ARMA(0,3),汽车整车行业选取ARMA(1,1)。

对五项行业分别构建ARMA(1,1)-GARCH(1,1)-偏t模型, ARMA(2,3)-GARCH(1,1)-偏t模型,ARMA(1,1)-GARCH(1,1)-偏t模型, ARMA(0,3)-GARCH(1,1)-偏t模型,ARMA(1,1)-GARCH(1,1)-偏t模型。 通过构建ARMA(p,q)-GARCH(1,1)偏t模型,条件均值方程消除了自相关与偏自相关,条件方差方程消除了ARCH效应。

为检验模型拟合效果, 以食品加工制造行业为例, 利用R语言生成食品加工制造行业的拟合效果图, 如图5所示。 从图5f可以看出, 边缘分布拟合效果很好。 由标准残差自相关图(图5c)、 标准残差平方项的自相关图(图5d)可以得出ARCH效应已消除。

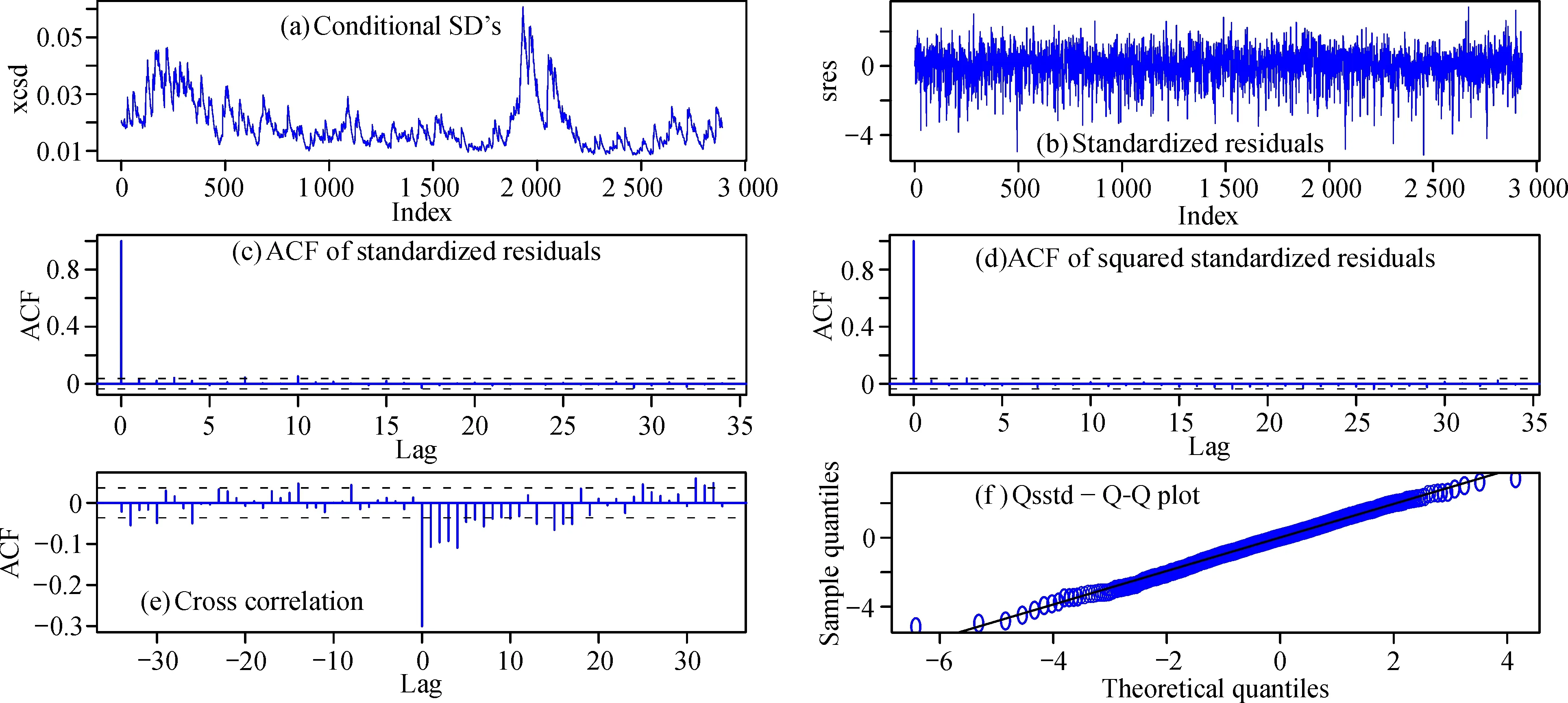
图5 食品加工制造行业ARMA(1,1)-GARCH(1,1)-偏t模型拟合图Fig.5 ARMA (1,1)-GARCH (1,1)-partial t model fitting map for food processing and manufacturing industry

2.5 VaR求解与Kupiec 检验

食品加工制造行业日收益率与VaR(99%)对比图(图6)表明，在99%的置信水平下, ARMA(1,1)-GARCH(1,1)-偏t模型进行的食品加工制造行业的风险度量效果较好, 其他行业亦如此。 对五项行业指数的构建模型进行Kupiec检验,结果如表5所示,模型所对应的失败天数越接近期望失败天数,表示模型拟合效果越好。 cc.LRp在5%的显著性水平下均大于0.05,在1%的显著性水平下均大于0.01,表明采用上述模型对五项行业拟合是合适的。

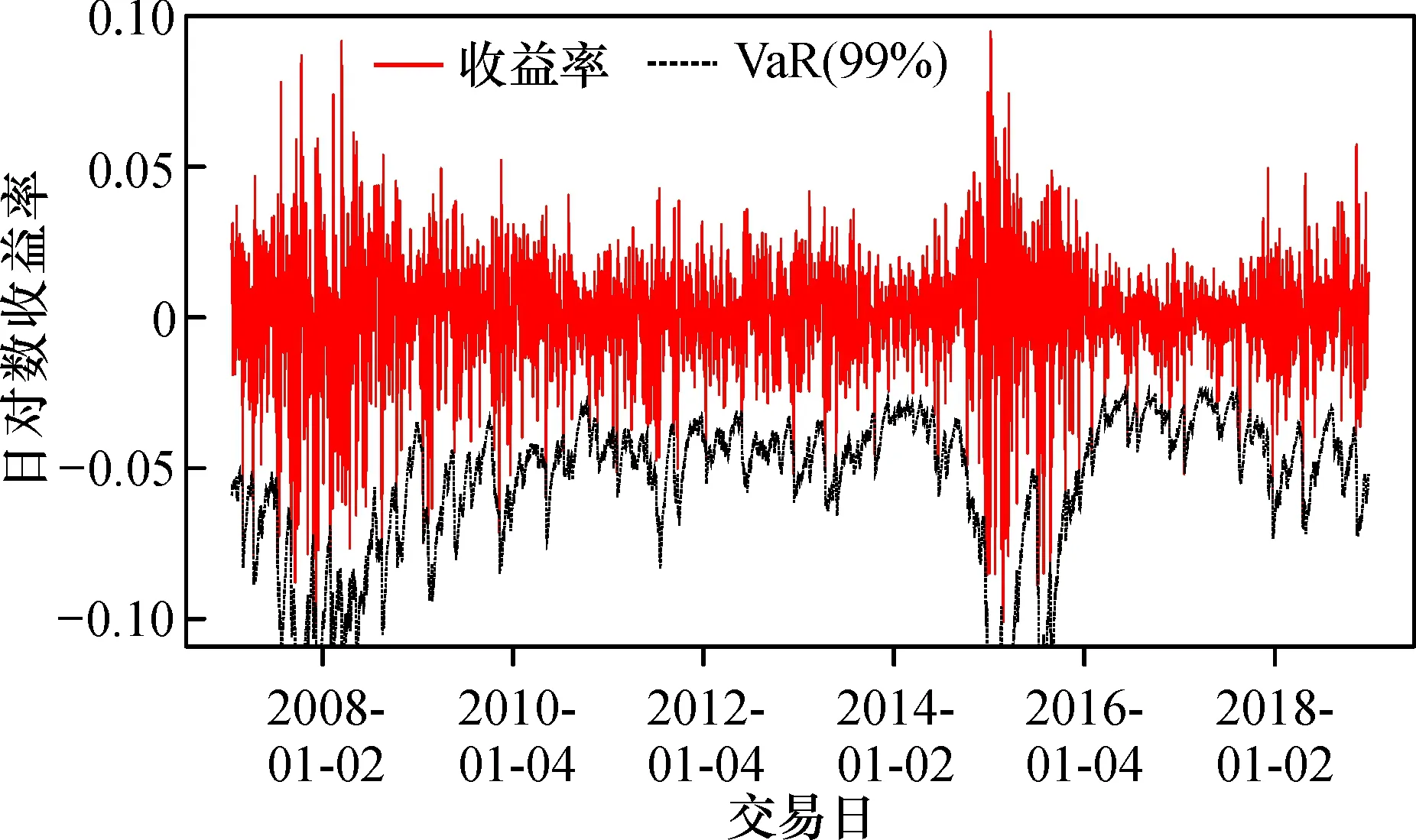
图6 食品加工制造行业日收益率与VaR(99%)对比Fig.6 Comparison of daily yield and VaR(99%) in the food processing and manufacturing industry

表5 各模型的Kupiec检验结果Table 5 Kupiec test results for each model

3 风险相依性研究

3.1 五项行业相关性研究

通过边缘分布拟合求得99%置信水平下的VaR,使用经验累积分布函数将其转化,对其求Kendall秩相关系数,如图7所示。

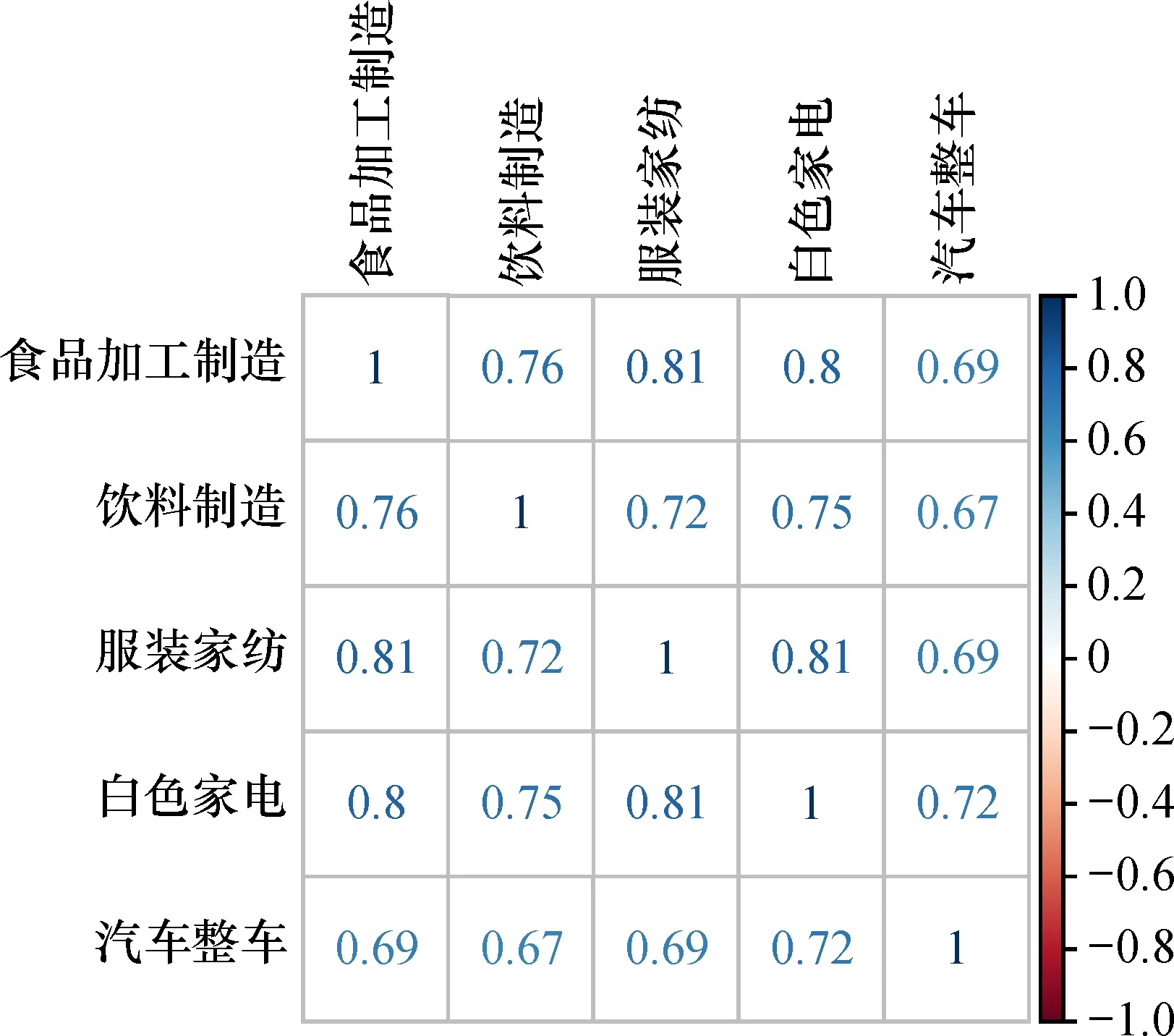
图7 五项行业VaR之间kendall秩相关系数图Fig.7 Kendall rank correlation coefficients among five industry VaR

可以看出,五项行业VaR之间相关系数均大于0,均为正相关。食品加工制造行业与服装家纺行业,服装家纺与白色家电行业相关性最强,相关系数为0.81。这说明吃好和穿好息息相关,穿好与住好紧密相连。饮料制造与汽车整车行业相关性最弱,相关系数为0.67，最大可能损失之间风险传染性最低的也是饮料制造行业与汽车整车行业。汽车整车与其他四项行业相关系数较小,均表明人们考虑问题的优先级,即先保障吃穿住,再完善其他。

3.2 C-Vine Copula 与D-Vine Copula的应用

使用C-Vine Copula对转换之后的VaR序列进行分析,如图8所示。

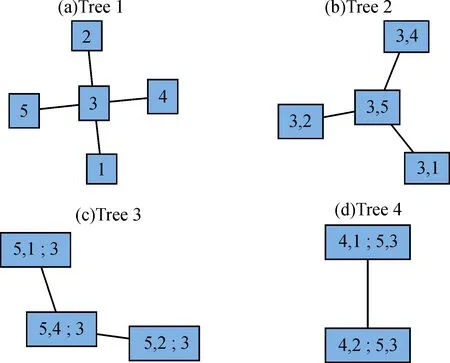
图8 C-Vine Copula生成树Fig.8 C-Vine Copula spanning trees

C-Vine Copula构建了4棵树,其中,数字1代表食品加工制造；2代表饮料制造；3代表服装家纺；4代表白色家电；5代表汽车整车。由第1棵树可知五项行业中最大可能损失之间风险传递的中心行业是服装家纺行业,第4棵树在给定服装家纺、白色家电、汽车整车的情况下,食品加工制造与饮料制造相连接,表明食品加工制造与饮料制造间相关性很弱。这与图7所显示结果并不一致,而且与常识不符。双重矛盾表明了C-Vine Copula模型并不是处理此类相关性的最优选择。若仅是找出风险传染的中心行业,C-Vine Copula模型是适用的,更进一步的研究则显得无能为力。因此,采用D-Vine Copula模型来进行研究,利用R语言生成D-Vine Copula生成树,如图9所示。

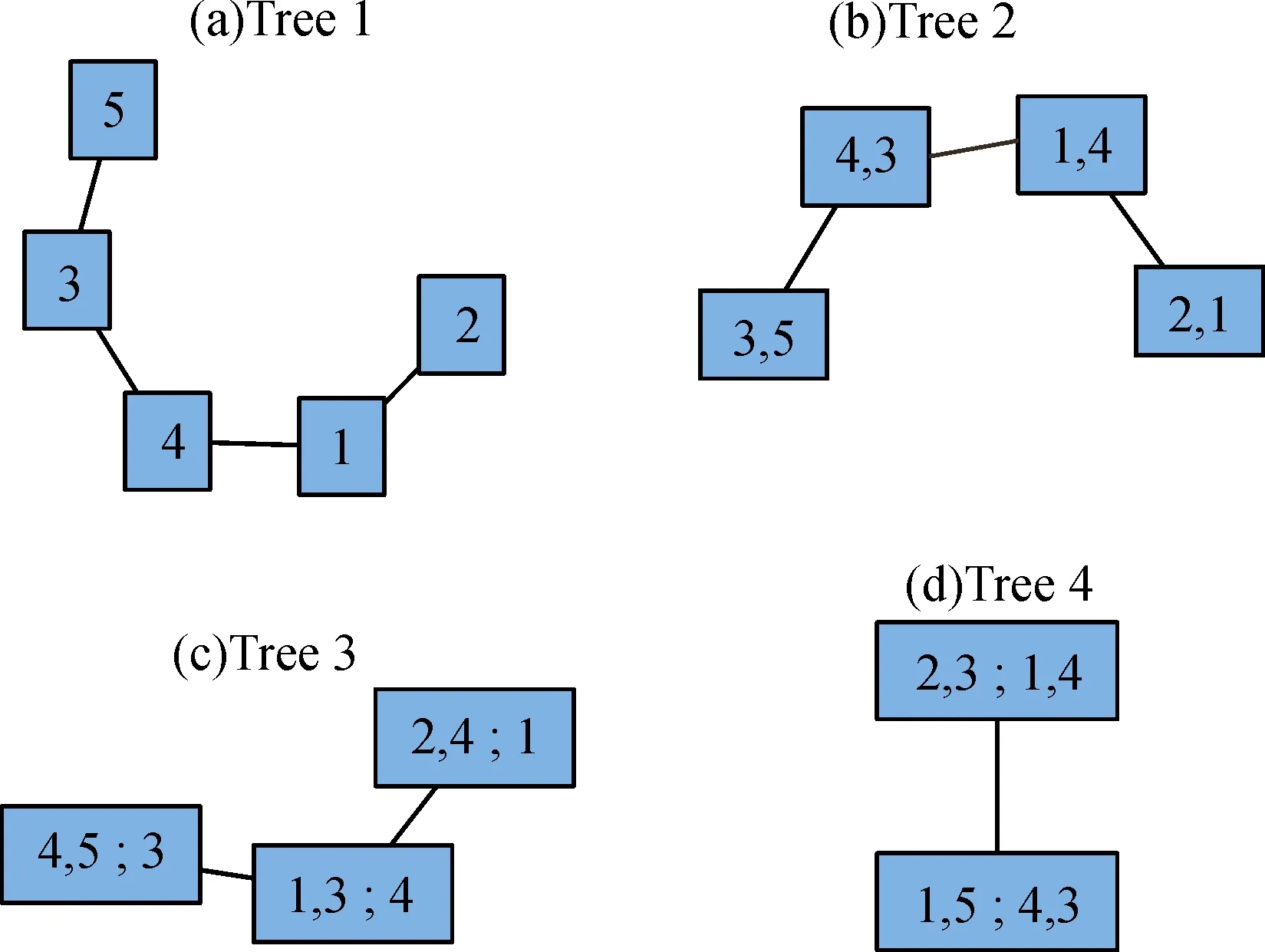
图9 D-Vine Copula 生成树Fig.9 D-Vine Copula spanning trees

D-Vine Copula构建了4棵树,由第1棵树可知饮料制造、汽车整车仅与一个行业相连,且饮料制造与汽车整车处于首尾但不相连的地位;由第4棵树可知,在给定食品加工制造、服装家纺、白色家电的情况下,饮料制造与汽车整车相连接,且tau值为0.13;以上两点均表明饮料制造与汽车整车行业相关性很弱,与图7所表达结果一致。人们多是在满足基本的吃饱穿暖住好的情况下再去考虑其他,吃饱穿暖住好即对应食品加工制造、服装家纺、白色家电。五项行业间存在不同相依性的原因在于不同社会阶层所迫切需要的服务是不同的,食品加工制造、服装家纺、白色家电多对应于中低端阶层,且相关性较强。而饮料制造与汽车整车多对应于高端阶层,但相关性较低。饮料制造以茅台为代表,汽车整车行业以新能源汽车为代表。茅台代表的是传统行业,新能源汽车代表新兴行业,传统与新兴的关系必不会如同传统行业内部一样强烈。

综合图7～9分析,图7与图9一致性更高,即D-Vine Copula模型表现更好,更能刻画五项行业的相依关系。现实当中很难出现某一行业为风险中心,向不同行业进行风险传染,大都是链式结构,即D-Vine Copula的形式。

4 结 论

采用ARMA-GARCH-偏t模型构建边缘分布,求得VaR并检验,对VaR序列采用经验累积分布函数变换,利用C-Vine Copula与D-Vine Copula模型对VaR进行相依性研究,C-Vine Copula表明服装家纺行业为风险传递的中心行业;D-Vine Copula表明饮料制造与汽车整车相关性最弱。D-Vine Copula相比于C-Vine Copula更能体现风险传染的相依性。

本文创新性的将ARMA-GARCH-偏t模型求得的VaR应用于风险的相依性研究,区别于以往利用收益率数据进行相依性研究,更能体现风险的相依性;局限性在于本文仅选择5个行业进行分析,未考虑到其他行业冲击带来的影响,仅从数据进行分析,未考虑突发事件,政策等因素的影响。进一步研究可将重大事件、政策的影响进行数据化,作为变量纳入分析,形成类似于恐慌指数(VIX)一样的指标。