基于TBC与GAMIT的多余长基线对高精度CORS数据解算精度分析

李宗婉,唐诗华,梁小龙,蒲 伦,肖 阳

(1.桂林理工大学 a.测绘地理信息学院;b.广西空间信息与测绘重点实验室,广西 桂林 541006;2.广西壮族自治区基础地理信息中心,南宁 530023)

在多余长基线对CORS基准站数据解算精度方面,相关的研究还较少。在CORS系统应用极广的当下,对这类研究具有一定的现实意义。

0 引 言

随着全球卫星导航系统(GNSS)技术与信息技术的融合与发展, 孕育出了二者集成的一种新的基础设施网络——连续运行参考站(continuously operating reference stations,CORS)[1]。 目前, 全国各省、市、自治区所建立的CORS系统采用的卫星导航系统主要是由三大系统构成, 即美国的全球定位系统(GPS)、 俄罗斯的格洛纳斯卫星导航系统(GLONASS)[2]和我国的北斗卫星导航系统(BDS)[3]。其中，我国建立的CORS系统具有定位精度高且分布均匀、高实时性和强稳定性等特点。

自全国CORS系统开始提供服务以来, 大量研究者参与到CORS基准站数据解算方法及影响其精度的各种因素研究当中, 如张芯等[4]研究了北斗系统(BDS)连续运行参考站的高精度基线解算及平差方法, 并开发相应处理软件, 对不同系统的基线解算精度进行了分析; 李兵等[5]分析了影响基线解算精度的诸多因素, 提出了“间距分区法”基线解算精度方案, 并与一般的分区方法对比分析, 验证了间距分区法相对于一般的分区方法具有较高的基线解算精度; 朱啟成等[6]对比分析了LGO+CosaGPS与HGO对控制网解算精度的影响, 结果表明, LGO的基线解算精度高于HGO, 在只有3个控制点网平差的解算结果中,CosaGPS的网平差精度略高于HGO, 未知点的平面坐标互差值较小; 李晓光等[7]就CORS站数据解算中所使用的对流层映射函数进行比较分析, 讨论卫星高度截止角变化及处理大量数据时映射函数的选取, 这对我国北斗导航定位系统应用映射函数具有参考价值。

由此,本文立足于生产实践,利用不同观测时间段的CORS基准站观测数据,分别采用TBC 4.10和GAMIT软件对观测数据进行基线解算,所得结果经重复基线较差和标准化的均方根误差两种标准检核后,再用COSA 6.0平差软件分别对两种处理结果进行网平差。通过同种平差方法定量分析不同基线解算方法、不同观测时间段下多余长基线对高精度CORS数据解算精度的影响。

1 试验数据及设计方案

1.1 数据来源

采用位于广西境内的8个CORS基准站2017年344～350共7个年积日的观测数据(已有精确的CGCS 2000坐标),同时也选取了同一板块的8个IGS站,即BJFS、HKSL、HKWS、LHAZ、PBRI、PIMO、SHAO、TWTF,与8个CORS基准站联合解算。选取5个CORS观测站JZ07、JZ38、JZ57、JZ62、JZ82作为已知点,3个CORS观测站JZ08、JZ21、JZ27作为未知点，所选基准站的平均间距为170 km,最小间距为72 km,最大间距为340 km。为了比较分析不同观测时长的CORS数据解算精度的结果,每天的数据分为7个观测时间段(02：00、 04：00、 06：00、 08：00、 12：00、 16：00、00：00)。图1为CORS站分布图。

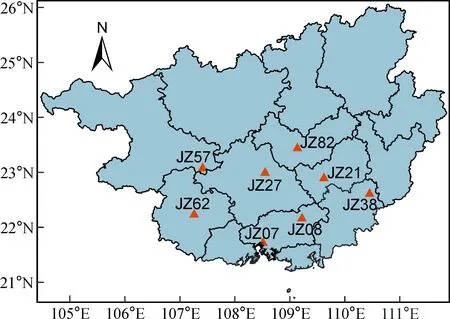
图1 CORS站分布示意图Fig.1 Distribution of CORS stations

1.2 软件选择

由美国麻省理工学院和斯克里普斯海洋研究所等机构联合开发的科研软件GAMIT/GLOBK应用广泛,用其进行基线解算可以使用不同的基线解类型来处理不同长度的基线[8-10]。GAMIT的整个数据处理过程分为两步:先编辑数据,得到观测文件x-file，再用x-file进行各种处理方案的参数估计[11]。但由于操作比较复杂,在实际生产应用中,更多的是采用操作相对简单的商用软件[12],如国外Trimble的TGO和TBC软件、Leica的LGO软件、Ashtech 的Solution软件等;国内南方测绘的GNSS数据处理软件、中海达的HGO软件、华测的Compass静态处理软件等。

TBC软件具有GPS基线处理、测量网平差、处理GPS和常规地形测量数据、生成DTM模型、等高线图等功能,其中基线解算流程可分为:建项并导入数据→设置参数→基线处理3步。TBC 4.0软件是旧版TBC软件的进阶版,目的是改进基线大于200 km的解算结果,提高了精度,降低了均方根值,模糊度固定率更高,可以实现更长基线的解算。新版的TBC 4.0软件支持多系统数据联合处理,并且可以选择独立于GPS卫星系统的其他卫星系统[13]。

考虑到实际生产应用,本文选择TBC软件进行基线处理,所得结果再与GAMIT软件处理的结果进行对比分析。进行整网平差时,把TBC和GAMIT处理得到的基线解算文件分别用COSA平差软件进行平差,以定量分析使用两种不同类型的软件时多余长基线对CORS数据解算的影响。

1.3 试验方案

为研究在不同观测时间下、不同解算软件时多余长基线对CORS数据解算精度的影响,采取以下两种方案对不同观测时间的数据进行处理。

方案一:①对8个CORS站2017年344～350共7个年积日的观测数据进行分析,将每日观测数据分为02：00、 04：00、 06：00、 08：00、 12：00、 16：00、00：00共7个观测时间段,作为数据一。②在步骤①的基础上引入8个IGS站,对IGS站数据处理方法与CORS站数据处理方法相同,作为数据二。③使用TBC软件分别对数据一和数据二进行基线处理。文献[14]针对不同截止高度角对基线解算结果的影响,得到当截止高度角取10°～15°时,基线解算结果最佳。解算前检查天线类型、量高方法、天线高度等是否有误。基线解算后对解算失败的基线进行观测时间段编辑,对观测质量较差的卫星实行禁用或局部不连续观测值的删除。④经TBC处理后得到的基线处理文件导入COSA平差软件中进行平差,得到平差结果。

方案二: 步骤①、 ②同方案一。 ③使用GAMIT软件分别对数据一和数据二进行基线处理。 使用GAMIT进行高精度基线解算时, 由于数据的处理方式不同, 所得到的结果也不尽相同。 文献[15]分析得出, 进行长基线解算时BASELINE解算效果较好。 该软件提供了两种长基线解算模型(LC-AUTCLN和LC-HELP), 文献[10]研究表明, 在电离层活跃的赤道附近采用LC-AUTCLN基线解较好。 ④经GAMIT处理后得到的基线处理文件导入COSA平差软件中进行平差, 得到平差结果。

本文进行基线解算时选择的参数见表1。

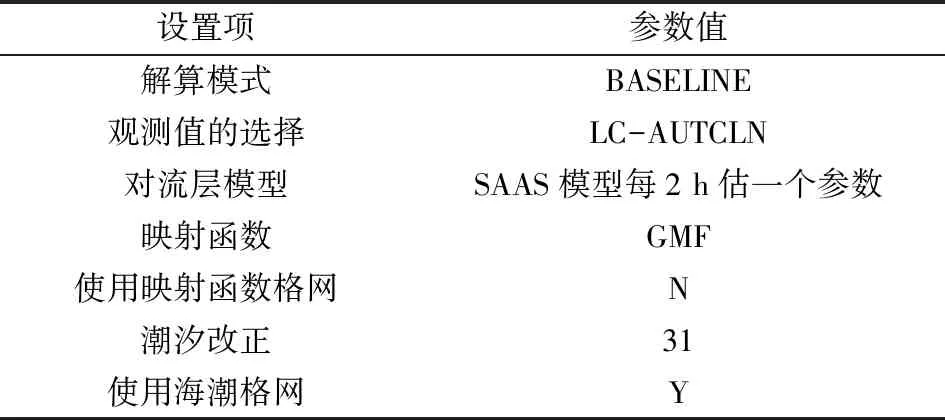
表1 基线解算控制参数的选择Table 1 Selection of control parameters for baseline sulotion

2 各解算方案的基线处理与精度分析

2.1 基于TBC+COSA(方案一)的基线解算

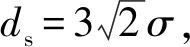
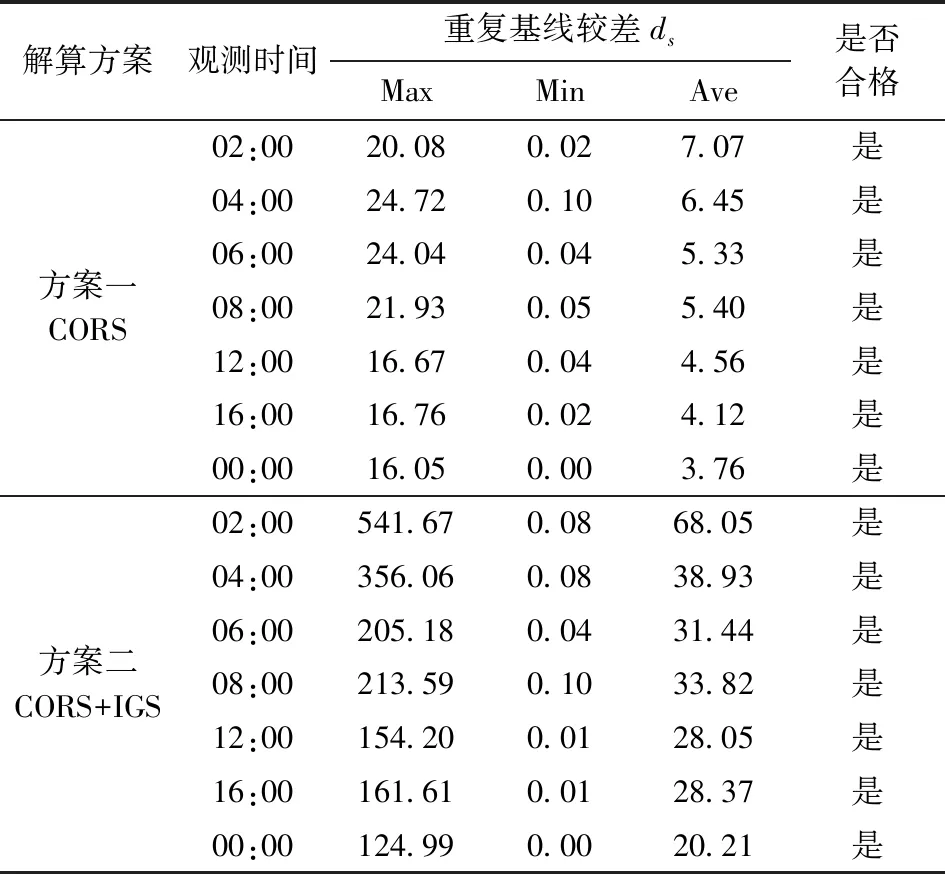
表2 CORS站2017年7个年积日(344～350)不同观测时段下重复基线较差Table 2 Difference of repeated baselines in different observation periods at CORS station for 7 doys in 2017 mm

可见,各个观测时间段的重复基线差较小,满足国家D级GNSS控制网规范要求。 经TBC处理后得到的CORS和CORS+IGS基线解算文件分别进行网平差,即可得到7个年积日不同观测时间段下的未知点的坐标。对平差结果再作进一步处理即可得到未知点高程。

2.2 基于GAMIT+COSA(方案二)的基线解算

方案二中预处理的数据经GAMIT基线处理后可得到基线解算文件, 为评估基线解算质量, 选择标准化均方根误差(NRMS)对结果进行评估。NRMS是衡量GAMIT基线解算质量的重要指标之一。 CORS、CORS+IGS站2017年7个年积日不同观测时间段的NRMS值如图2所示。各个区间的NRMS值均在0.2以下,符合高精度基线解算的要求。

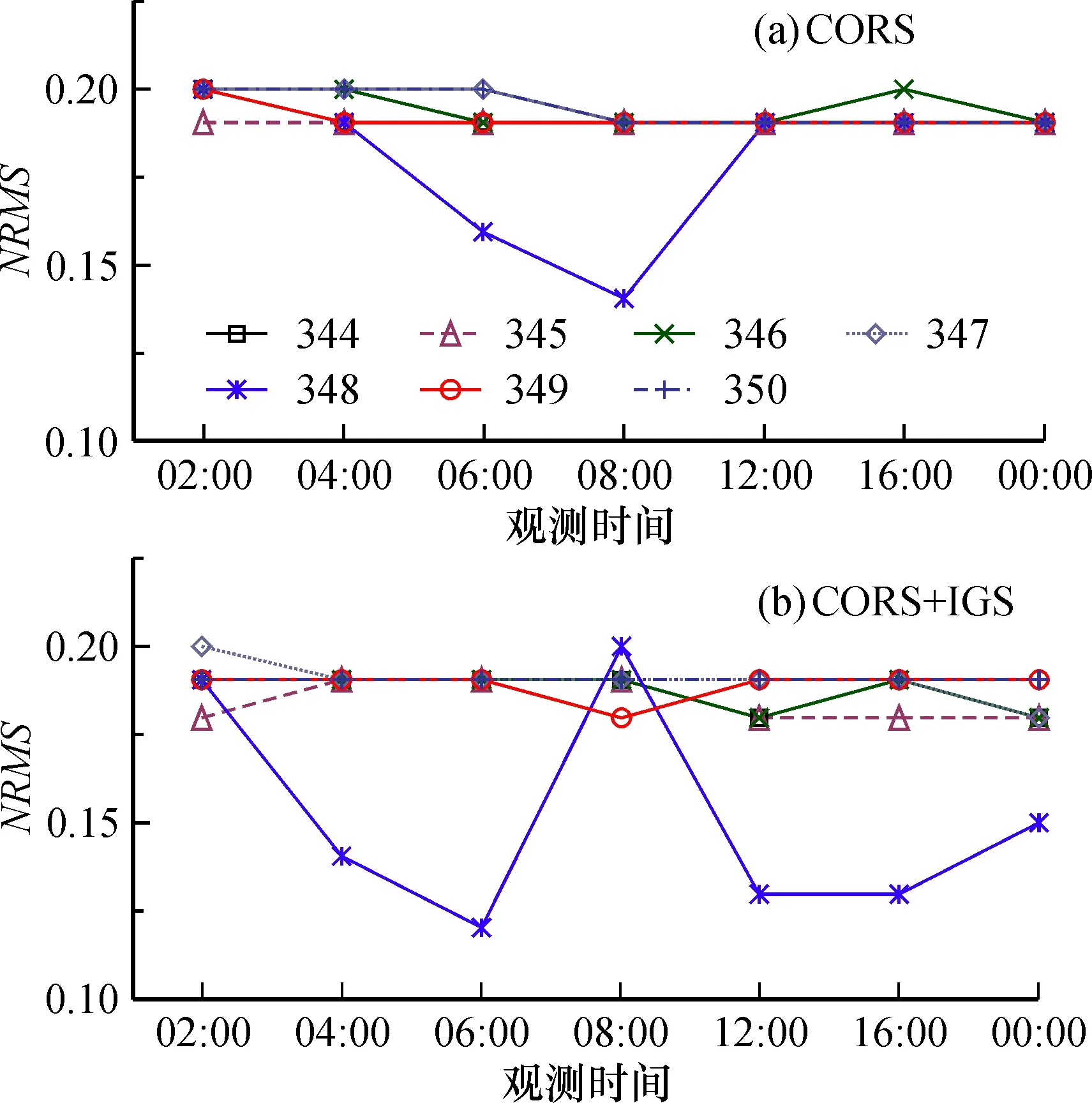
图2 2017年7个年积日不同观测时间CORS(a)和 CORS+IGS(b)基线解算的NRMS值统计Fig.2 NRMS statistics of CORS(a) and CORS+IGS(b) baseline solution in different observation periods of 7 doys in 2017

与方案一平差过程类似,对CORS和CORS+IGS基线解算文件分别进行网平差,即可得到7个年积日不同观测时间段下的未知点的坐标。对平差结果作进一步处理可得到未知点高程。

2.3 精度分析

利用COSA软件进行网平差计算时, 导入基线解算文件, 控制网等级选择D级。 输入已知点的大地坐标后, 分别进行三维无约束平差及三维约束平差, 经平差后可得到未知点坐标等信息。 为了解两种方案不同观测时间段下的多余长基线对CORS数据解算精度的影响, 本文将对平差结果进行分析。

2.3.1 坐标精度分析 未知点坐标精度绝对值在两种方案不同观测时间段下的最大值和平均值统计见表3。

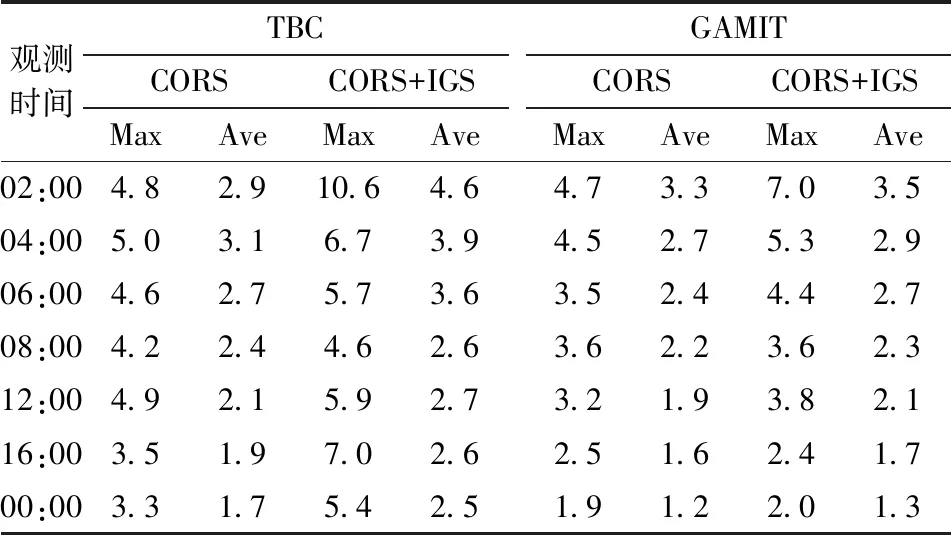
表3 两种软件不同解算方案各观测时间段下未知点坐标精度Table 3 Coordinate accuracy of unknown points at each observation periods under different baseline solution of the two softwares mm

可知,从整体上看,无论是TBC还是GAMIT处理的基线解算,在CORS站的基础上引入IGS站,所得未知点坐标精度的最大值和平均值均劣于CORS站,表明多余长基线会影响CORS站数据解算精度,观测时长较短时,其影响尤为突出;随着观测时长的增加,多余长基线的影响呈减小的趋势。对两种方案解算质量分析可知,GAMIT的基线解算质量优于TBC,在仅解算CORS站的情况下,同一观测时间段两种方案的未知点坐标精度平均值最大差值为0.5 mm;引入IGS站后,平均值最大差值为1.2 mm,TBC基线解算所得精度与GAMIT差异不明显。

2.3.2 高程精度分析 未知点高程平差结果与真值之差在两种方案不同观测时间段下的最大值和平均值统计见表4。

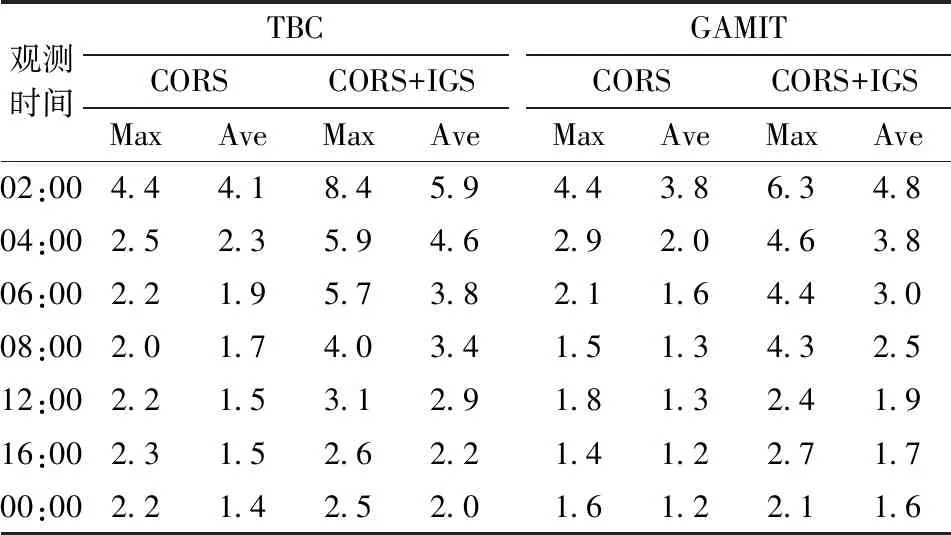
表4 两种软件不同解算方案各观测时间段下未知点高程精度Table 4 Elevation accuracy of unknown points at each observation periods under different baseline solution of the two softwares mm

可知,由TBC或GAMIT处理的基线解算,经过平差后进一步处理得到的高程,其精度是CORS站优于CORS+IGS站,说明多余长基线会影响CORS数据解算精度。除个别数值外,未知点高程平差结果与真值之差随着观测时长的增加而减小。对两种方案的解算质量进行分析可知,不同观测时间段下由GAMIT参与基线解算经平差后得到的高程优于由TBC参与基线解算经平差后得到的高程。在仅解算CORS站的情况下,同一观测时间段两种方案的未知点高程平差结果与真值之差最大为1.3 mm,平均值最大差值为0.4 mm;引入IGS站后,高程平差结果与真值最大差值为4.9 mm,平均值最大差值为1.1 mm。TBC的解算精度与GAMIT相比有一定的差距。

3 结 论

本文通过两种方案对2017年344～350共7个连续年积日不同观测时间段的CORS观测数据进行了分析,引入了IGS站以研究多余长基线对CORS站数据解算精度的影响。通过实验得知,无论基线解算过程采用的是TBC或是GAMIT,多余长基线都对CORS站数据解算精度产生影响,且观测时长较短时,影响尤为明显。随着观测时间增加,影响逐渐减小。在软件解算质量方面,TBC的解算精度虽逊色于GAMIT的解算精度,但两者的解算结果差异不大。TBC作为一款商用软件,其操作简便且界面实体化,在实际生产应用方面有一定的优势。本次实验进行网平差时采用的控制网级别是D级,经平差后得到的未知点坐标和高程皆满足国家标准,符合实际生产要求。