不同间距下溶洞对分离式隧道稳定性的影响

朱翔宇,张乐文

(1.桂林理工大学 土木与建筑工程学院,广西 桂林 541004;2.山东大学 海洋研究院,山东 青岛 266237)

0 引 言

岩溶在我国西南地区分布较为广泛, 由此带来的工程地质问题也较为突出。 随着社会经济的发展, 在岩溶区修建隧道的需求也愈加强烈。 然而, 关于在岩溶区修建隧道的研究较少, 且多集中于单独隧道条件。 在数值模拟研究方面,李红卫[1]利用ABAQUS分析了隧道底部存在溶洞时, 溶洞的尺寸、 溶洞与隧道长轴的关系以及溶洞与隧道的间距对施工过程中隧道结构受力的影响, 以及围岩产生的相应位移； 李培楠等[2]研究了溶洞的不同分布位置、 尺寸大小及其与隧道间的净距对地铁施工过程中围岩稳定性的影响； 唐侦湛等[3]利用 FLAC 软件研究了隧道周边无溶洞 、溶洞位于隧道侧部、 顶部和底部 4种工况下隧道的稳定性状况； 宋建禹[4]利用有限元分析软件ANSYS 11.0对溶洞与开挖隧道的相对位置、 溶洞的跨度、 溶洞的形状变化、 岩体的黏聚力、 内摩擦角、 容重、 泊松比、 弹性模量以及隧道或溶洞的埋深等因素与隧道围岩稳定性的关系进行研究； 周雪铭等[5]以隧道开挖中处治结构和围岩稳定性为研究对象, 分析了在隧道开挖过程中处治结构的受力特性,以及隧道围岩的位移； 宋战平等[6]分析了隧道顶部存在不同尺度和距离的既有隐伏溶洞对圆形隧道围岩应力、 位移和支护结构内力的影响； 李志义等[7]以宜万铁路齐岳山隧道工程为背景, 论证了当溶洞处于隧道掌子面前方时, 溶洞尺寸、 岩体厚度以及不同的岩溶水压力对隧道的变形破坏规律。

传统上认为, 分离式隧道由于其中间存在较大的间距, 隧道之间并不会产生太大的相互影响, 因此, 其设计与施工基本按单独隧道方法进行。 在岩溶区修建分离式隧道的研究成果报道甚少，并且在岩溶区修建分离式隧道时, 隐伏溶洞会引起隧道应力应变状态的改变, 原本针对非岩溶区或单独隧道所得出的分析结果也随之产生偏差。 本文以圆形隧道为例, 利用FLAC3D软件,分析了既有隐伏溶洞存在于隧道之间时,对分离式隧道围岩应力、变形所产生的影响,初步揭示了溶洞对分离式隧道稳定性影响大小随着隧道间距改变而改变的规律,以便为类似工程建设提供参考。

1 研究方案

为研究在不同间距下, 溶洞对分离式隧道稳定性影响的规律, 需建立多个模型进行模拟。 由于隧道为线状工程,其长度远大于宽度与高度,因此模型按平面问题处理。为了简化计算,在建立模型时,将模型假设为长方体(洞长为y, 宽x, 高z), 横截面(xoz平面)为长方形, 并假设溶洞和隧道的截面均为圆形, 溶洞处于分离式隧道之间两隧道连线的中点, 不同的模型仅改变两隧道的间距, 其他条件不变(即各模型仅在x方向改变, 在z和y方向不变)。在确定溶洞与隧道截面尺寸时,主要考虑实际隧道工程并参考有关文献,选定溶洞半径为3 m,隧道半径为6 m。模拟时取洞轴方向y=20 m,高度z=74 m(5倍洞径范围内),宽度x在94～102 m。各模型具体尺寸见表1,隧道间距为12 m的隧道模型如图1所示。

表1 不同隧道间距下的模型尺寸Table 1 Parameters of model under different tunnel distances m

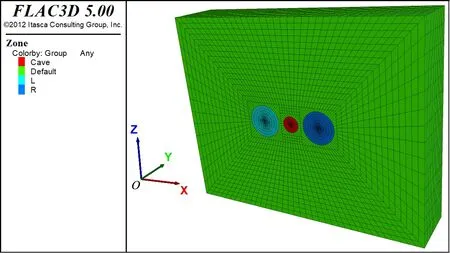
图1 隧道间距为12 m时的计算模型Fig.1 Calculation model for tunnel distance of 12 m

对于每个模型,其模拟方案均为:① 按溶洞处于填充状态(即无溶洞)建模;②计算自重应力,并将模型位移、加速度变量设为0,以模拟围岩的初始应力状态(天然条件下的稳定状态); ③模拟隧道开挖(无溶洞时); ④读取步骤①中所建模型,并将溶洞部分的岩层挖去; ⑤重新计算岩层自重应力, 并将模型位移变量及加速度变量设为0; ⑥模拟隧道开挖(有溶洞时)。

按照上述步骤进行FLAC3D数值模拟,得到相应的应力和位移云图,以隧道间距为12 m时为例,将有无溶洞的应力和位移云图进行对比来分析溶洞对隧道稳定性的影响。之后,分别对比不同模型随着隧道间距的改变,溶洞对隧道稳定性影响的变化规律。

模拟计算时,边界条件的确定、初始应力场的施加、参数的选取、研究对象的本构模型以及屈服准则的确定都非常重要。本次模拟所选取模型的约束条件为:在水平方向边界进行水平位移约束,在模型底部进行竖向位移约束,模型顶面是自由面,模型整体受到围岩自重作用影响。模拟的隧道为浅埋隧道,初始应力为上覆岩土层的自重应力。围岩采用理想弹塑性材料,屈服准则采用 Mohr-Coulomb 准则。综合参考多个类似工程文献资料后,确定了围岩参数，具体见表2。

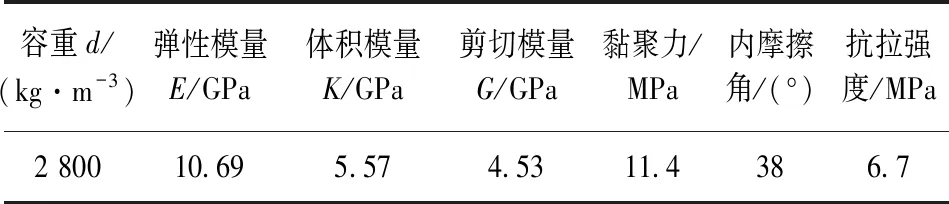
表2 数值模拟围岩参数Table 2 Surrounding rock parameters in numerical simulation

2 溶洞对分离式隧道影响分析

2.1 溶洞对分离式隧道围岩应力影响分析

经过FLAC3D计算,分别得到隧道围岩的最大主应力、最大剪应力和位移云图(图2—4)。图2为分离式隧道围岩的最大主应力云图。当分离式隧道中间存在溶洞时,隧道围岩应力整体上都有增加的情况。进一步分析可以发现,无论是否存在溶洞,隧道周围的最大拉应力往往都分布于隧道的顶部及底部洞壁处,且隧道顶部的拉应力要大于隧道底部的拉应力;最大压应力则往往距离洞壁有一段距离。在没有溶洞时,虽然两个隧道之间的围岩受到两个隧道的共同作用,但是由于拥有足够的围岩厚度,因此压应力仅略大于外侧。当中间有溶洞时,由于隧道间围岩厚度的减少,溶洞也会在水平方向产生一定的压应力,因此中间部分的压应力集中分布在隧道与溶洞之间,在数值上有明显的增加。

图2 无溶洞(a)和有溶洞(b)时最大主应力云图Fig.2 Contour of max principal stress without(a)and with karst cave(b)

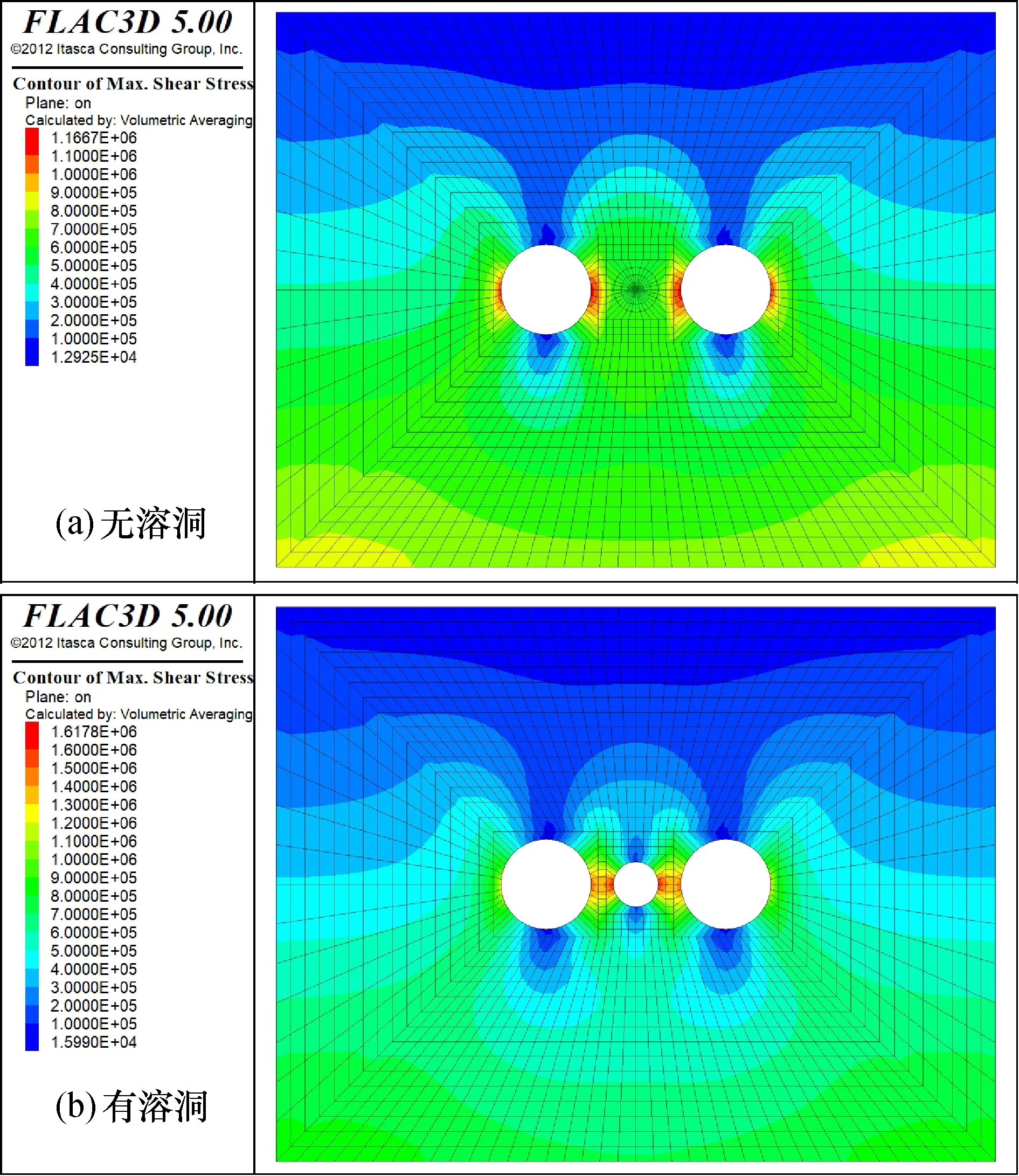
图3 无溶洞(a)和有溶洞(b)时最大剪应力云图Fig.3 Contour of max shear stress without(a)and with karst cave(b)

通过FLAC3D进行分析后可知,当隧道附近存在溶洞时, 其洞壁处最大拉应力有较快增长, 而压应力增长不大。 当隧道中间存在溶洞时, 其顶部的最大拉应力由原来的36.9 kPa增加到60.7 kPa, 增幅达到64.5%； 其底部附近的最大拉应力由原来的6.8 kPa增加到28.2 kPa, 增幅达到314.7%。 当隧道中间不存在溶洞时, 隧道洞壁处的最大压应力为221.2 kPa, 隧道附近围岩的最大压应力为400.6 kPa； 当隧道中间存在溶洞时,洞壁处的最大压应力为257.4 kPa,增长率为16.4%;隧道附近围岩的最大压应力增长到了440.2 kPa,增长率为9.9%(图5)。

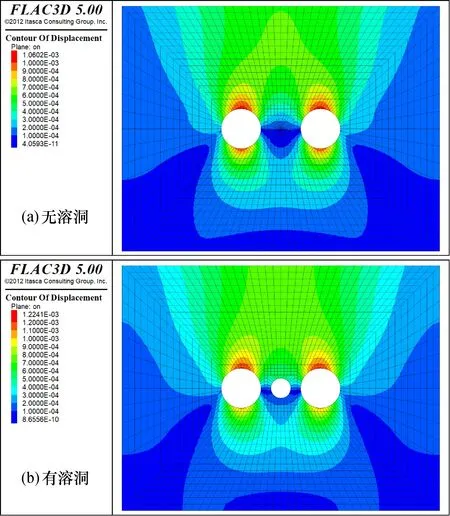
图4 无溶洞(a)和有溶洞(b)时的位移云图Fig.4 Contour of displacement without(a)and with karst cave(b)

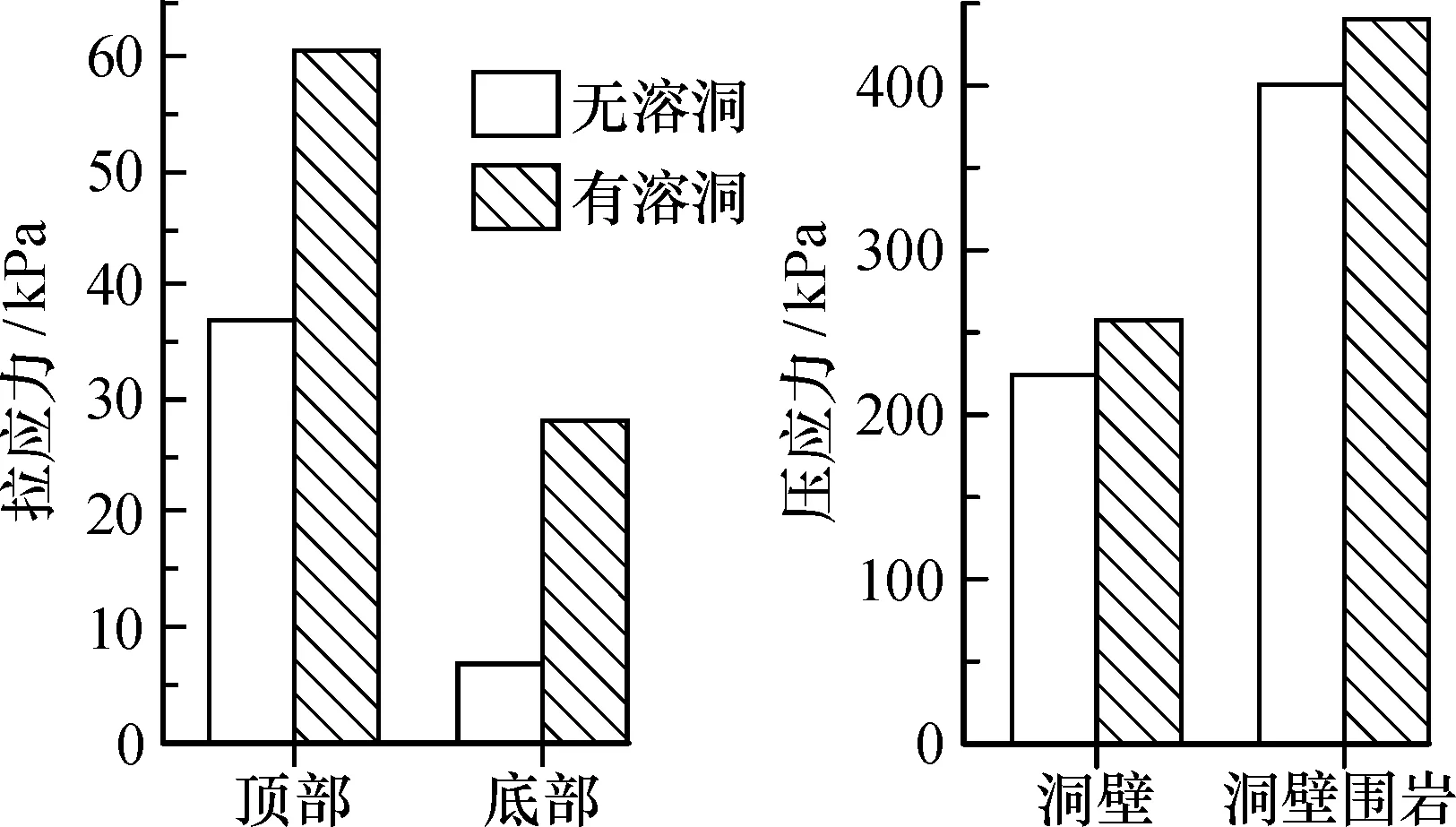
图5 隧道洞壁处最大拉应力与最大压应力变化对比Fig.5 Comparison of maximum tensile stress and maximum compressive stress at tunnel wall

图6 隧道顶部及底部位移变化对比Fig.6 Changes of upper and lower directions of tunnels

可以看出,当分离式隧道中间不存在溶洞时(图3a),隧道间虽然也存在着互相影响,但由于相距足够远,隧道两侧围岩的剪应力值大致相等。当隧道中间存在溶洞时(图3b),隧道围岩的剪应力均有所增加，而且由于溶洞一侧围岩的厚度变小,其剪应力增长量远大于其他部位的剪应力增长量。

2. 2 溶洞对分离式隧道变形影响分析

从图4可见, 当隧道中间存在溶洞时, 隧道围岩的位移量均有不同程度的增加。 由于岩石的抗拉强度明显小于抗压强度, 因此, 虽然分离式隧道竖直应力较小, 但产生的位移却较大。 同时, 由于隧道围岩顶部拉应力大于底部拉应力, 故其顶部的位移增量大于底部的位移增量。为直观起见, 通过FLAC3D分析出隧道顶、 底洞壁处的位移变化后, 制成对比直方图(图6)。此外, 通过对云图的分析还可看出, 当有溶洞时, 溶洞附近及上部岩层的位移均有所增加, 若两隧道中间的上方存在既有建筑物, 则需要考虑对既有建筑物的保护。

3 溶洞对隧道间距变化的规律

根据模拟计算结果可知,在给定条件下,分离式隧道围岩的拉应力主要分布在隧道的顶部和底部,其中拉应力最大值多分布在隧道顶部,但底部的拉应力增长很快。当这些部位岩体由于某些原因使其强度降低或节理裂隙较发育时,容易产生拉裂破坏或使拉裂破坏区增大,导致冒顶等工程事故的发生,因此,隧道设计施工时需要对其进行考虑,而压应力最大值主要分布在隧道之间,不在洞壁处。由于进行隧道稳定性分析时,需要分析围岩的最大主应力、剪应力和位移等,因此,在对比由隧道间距对隧道稳定性所产生的影响时,只对分离式隧道顶部和底部的拉应力、洞壁处和围岩的压应力最大值以及最大位移量随隧道间距的变化进行分析。将溶洞处于不同间距时的模型代入FLAC3D进行计算。

3.1 围岩应力状态分析

对比图7的5组模型可以看出,溶洞对隧道围岩应力状态影响非常大。当无溶洞时,由于隧道中间仍然存在着较为完整的岩体,无论隧道的间距如何改变,隧道围岩的应力状态都不会发生明显变化,即使低于规范所要求的最小间距(12 m)时,洞壁处的拉应力也没有产生明显变化。

图7 洞壁处最大拉应力随隧道间距变化规律Fig.7 Variation of maximum tensile stress at tunnel wall with tunnel spacing

但是,当隧道中间存在溶洞时,由于溶洞降低了围岩的实际厚度,使围岩的应力状态发生变化。随着隧道间距的增加,隧道围岩的应力增量出现明显下降,并最终趋向于无溶洞状态。当隧道相距约为隧道开挖断面宽度的83%(10 m)时,洞壁处的最大拉应力增长率达到了102%;当隧道间距增加到1倍洞径(12 m)开挖断面宽度时,增长率下降到65%;接着,最大拉应力增长率随着隧道间距的增长大致呈现稳定下降的趋势,当隧道间距达到1.5倍洞径(18 m)时,增长率已经不超过15%了。

从图8可知,溶洞的存在对隧道底部的拉应力最大值有很大影响。无溶洞时,洞底最大拉应力较小,其值虽随隧道间距的增加略有增长,但总体变化不大。有溶洞时,洞底最大拉应力值有了很大增长,隧道间距越小,拉应力增长越大；随着隧道间距的增加而减小,并逐渐趋向于与没有溶洞相一致。

图8 隧道底部最大拉应力变化规律Fig.8 Variation of maximum tensile stress at the bottom of tunnel

对比图9的5组数据可以看出, 无溶洞时, 随着隧道间距的增加, 洞壁处的压应力出现缓慢下降的趋势, 但变化不明显。 有溶洞时, 其对洞壁处压应力的影响也具有与无溶洞时类似的规律： 当隧道间距约为隧道开挖断面宽度的83%(10 m)时, 洞壁处最大压应力的增长率约为19.8%; 随着间距的增加, 洞壁处压应力逐渐减小, 当隧道间距增长至1.5倍开挖断面宽度(18 m)时, 其增长率已经减小到约7.7%了。

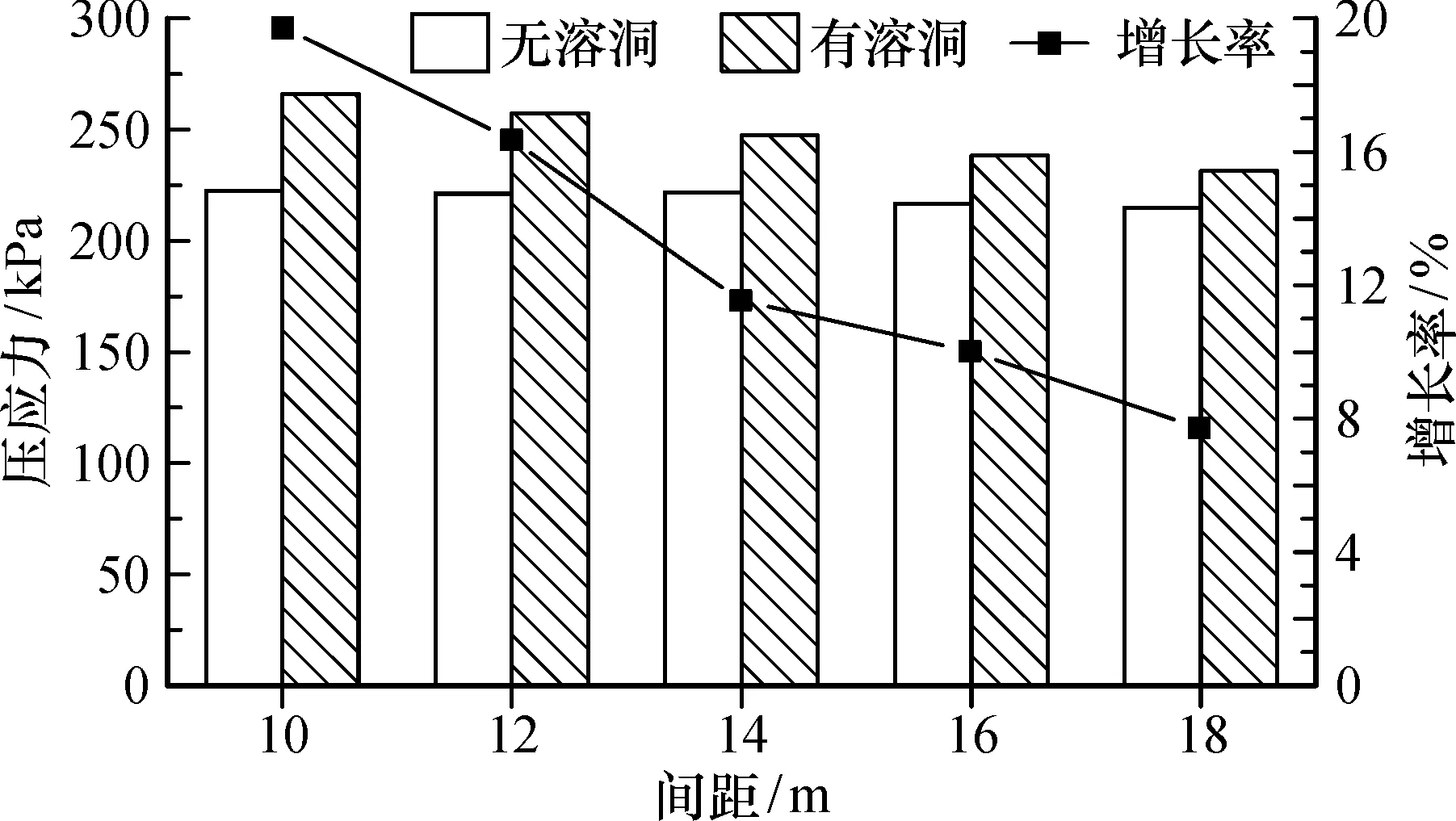
图9 洞壁处最大压应力随隧道间距变化规律Fig.9 Variation of maximum pressure stress at tunnel wall with tunnel spacing

从图10可知,虽然从增长率上看,拉应力的增长速度明显大于压应力；但是从增长量上看,则呈现出压应力普遍大于拉应力的状态。对比顶部和底部的拉应力,可以看出当分离式隧道距离较近的时候,顶部的拉应力增长量要大于底部,但是当隧道间距达到约1.3倍隧道开挖断面宽度(14～16 m)的时候,顶部和底部的增量就趋于一致了;当间距达到1.5倍(18 m)开挖断面时,已经很难区分两者的差异,其数值也近似相等。

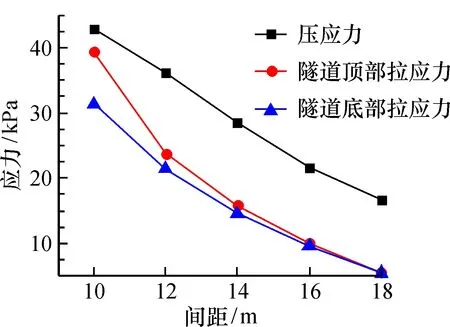
图10 主应力增量变化曲线Fig.10 Incremental variation curves of principal stress

从图11中可以看出,围岩中最大压应力的变化规律则与最大拉应力、洞壁处最大压应力的变化规律有较大差异:在存在溶洞的情况下,当隧道间距约为隧道开挖断面宽度的83%(10 m)时,围岩的最大压应力不但没有增加,反而略有减小；当隧道间距达到1倍隧道开挖断面宽度(12 m)时,围岩最大压应力才开始增加；随着隧道间距增加至隧道开挖断面距离约1.17倍(14 m)时,围岩最大压应力的增长率也增加至30.4%；之后,随着间距的增加,溶洞对隧道的影响不断减小,最大压应力的增长率也在不断减小,直至间距为1.5倍隧道开挖断面宽度(18 m)时的21.8%。

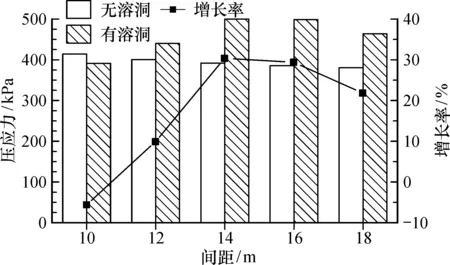
图11 围岩最大压应力随隧道间距变化规律Fig.11 Variation of maximum pressure stress of surrounding rock with tunnel spacing

3.2 围岩变形状态分析

从图12无溶洞模拟结果看, 在其他条件不变的情况下, 随着隧道间距的增加, 围岩的最大位移量也在逐渐降低, 但降幅非常缓慢。 有溶洞时, 会对围岩的位移量产生影响。 由于溶洞对围岩应力状态的影响程度受隧道间距的影响较大, 隧道洞壁处的最大位移量也随隧道间距发生改变。 当隧道间距为隧道开挖断面宽度的83%(10 m)时, 隧道位移增长率最大, 约为23.2%； 当间距增加到1倍隧道开挖断面宽度(12 m)时,增长率急剧减小, 下降到了15.1%；之后, 隧道间距继续增加, 位移增长率稳步下降, 直至1.5倍(18 m)隧道开挖断面宽度时的6.9%。

图12 洞壁处最大位移变化情况Fig.12 Variation of maximum displacement at tunnel wall

由图13可见, 无溶洞时, 隧道在水平方向的位移随着隧道间距的增加而略有减小。 有溶洞时, 随着隧道间距的增加, 隧道水平方向位移增长率先是快速下降到0左右, 接着出现反向增长。

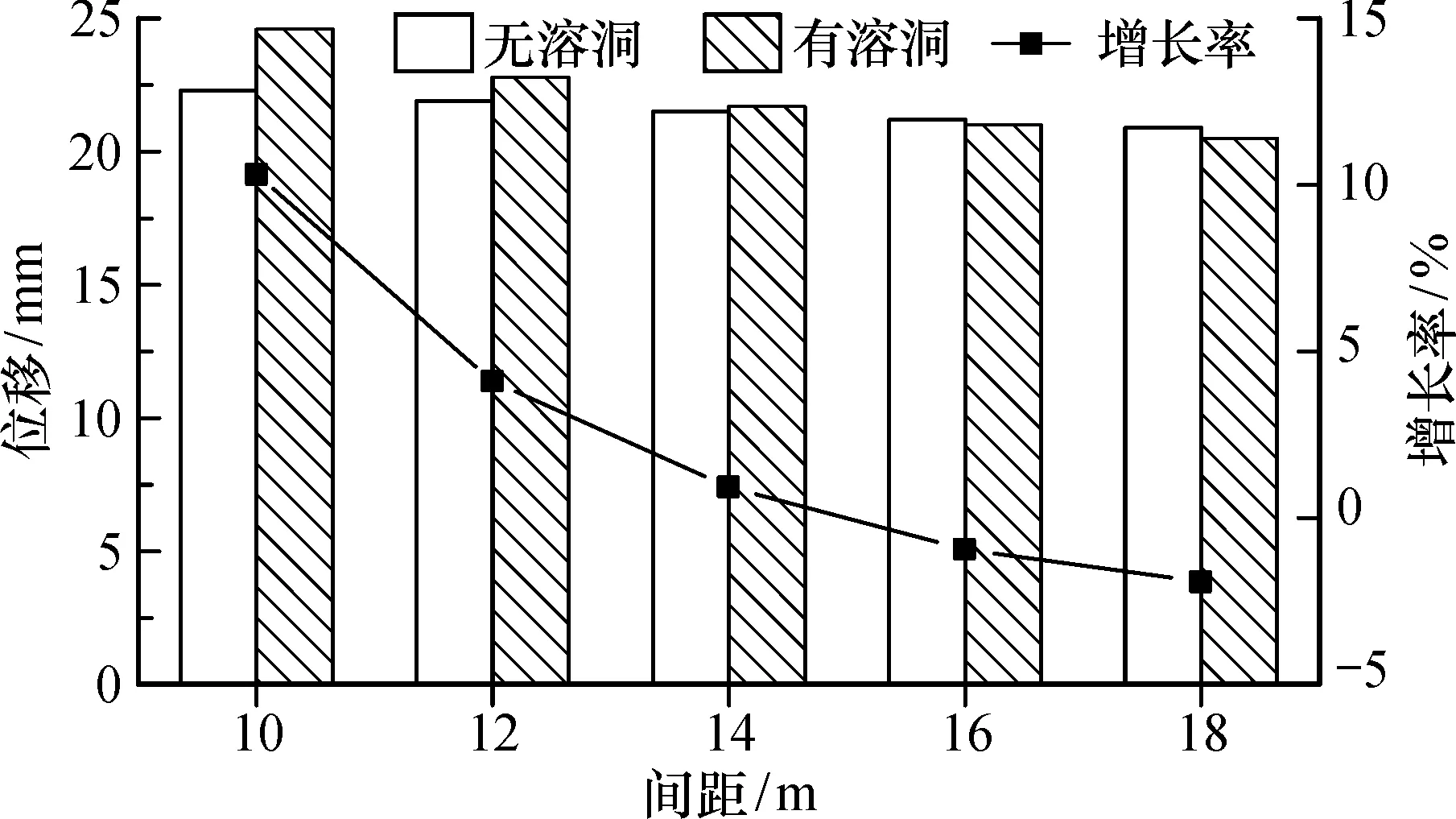
图13 隧道水平方向最大位移变化规律Fig.13 Variation of maximum displacement in horizontal direction of tunnels

对比图14、图15可以发现,当存在溶洞时,随着隧道间距的增加,隧道顶部和底部围岩的位移增长率也呈现出先快速下降,而后缓慢而平稳下降的情况。由于隧道顶部的应力比底部大,因此隧道顶部的最大位移也大于底部的位移。

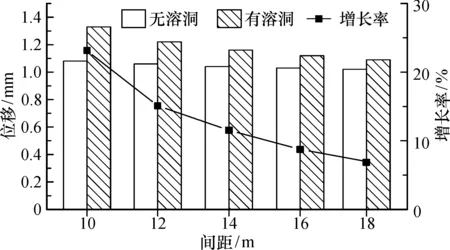
图14 隧道顶部围岩竖直方向最大位移量变化规律Fig.14 Variation of maximum displacement in vertical direction of surrounding rock on the top of tunnels

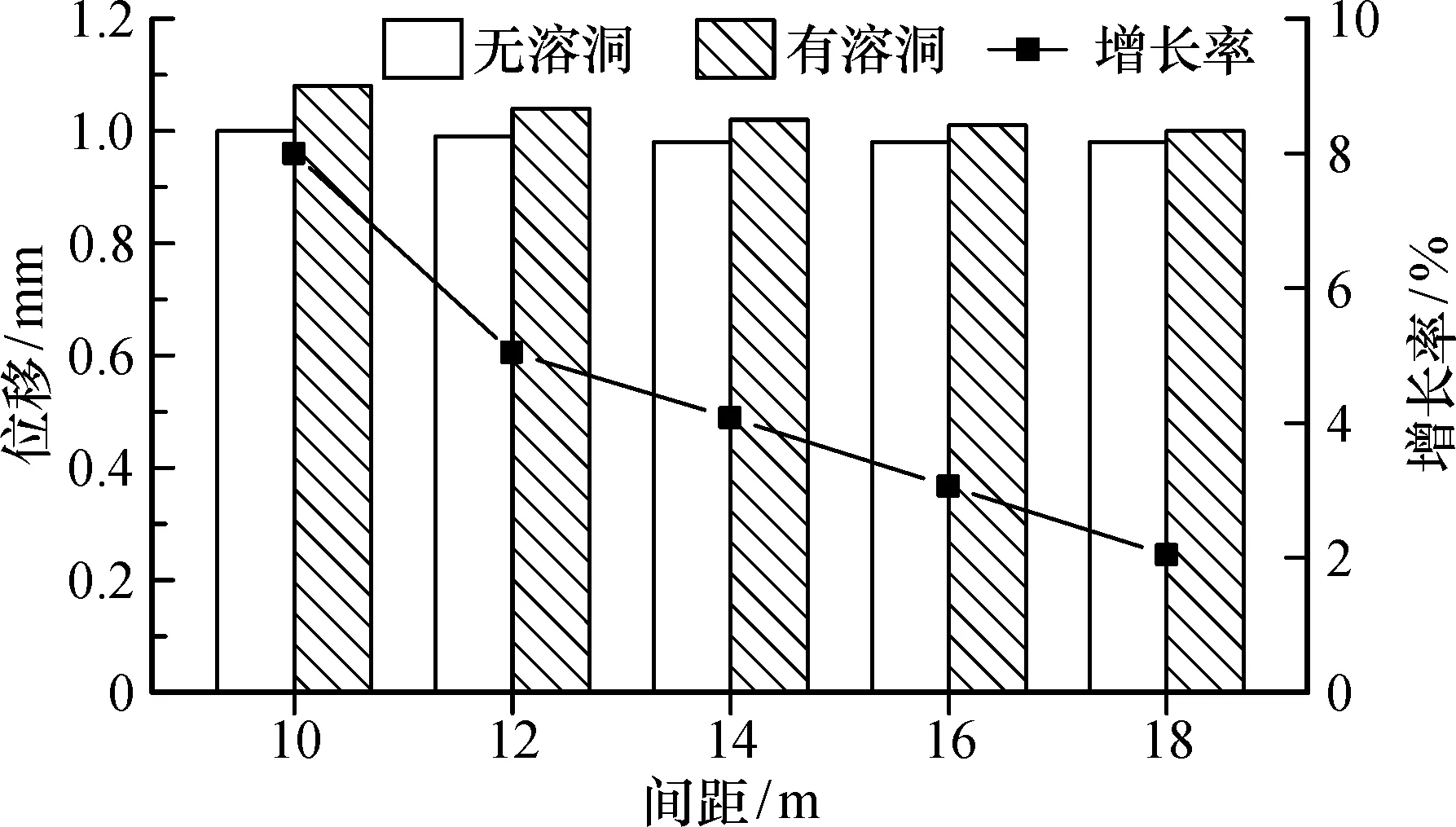
图15 隧道底部竖直方向最大位移量变化规律Fig.15 Variation of maximum displacement in vertical direction at the bottoms of tunnels

对比图16中的3组位移增量变化曲线可知,溶洞对隧道位移的影响程度对于隧道的各个部位而言各不相同。溶洞对隧道顶部位移增长量的影响最大,其次是隧道底部的位移增长量,最后是隧道水平方向外侧。因此,在岩溶区施工时,需要加强对隧道顶部变形监测。

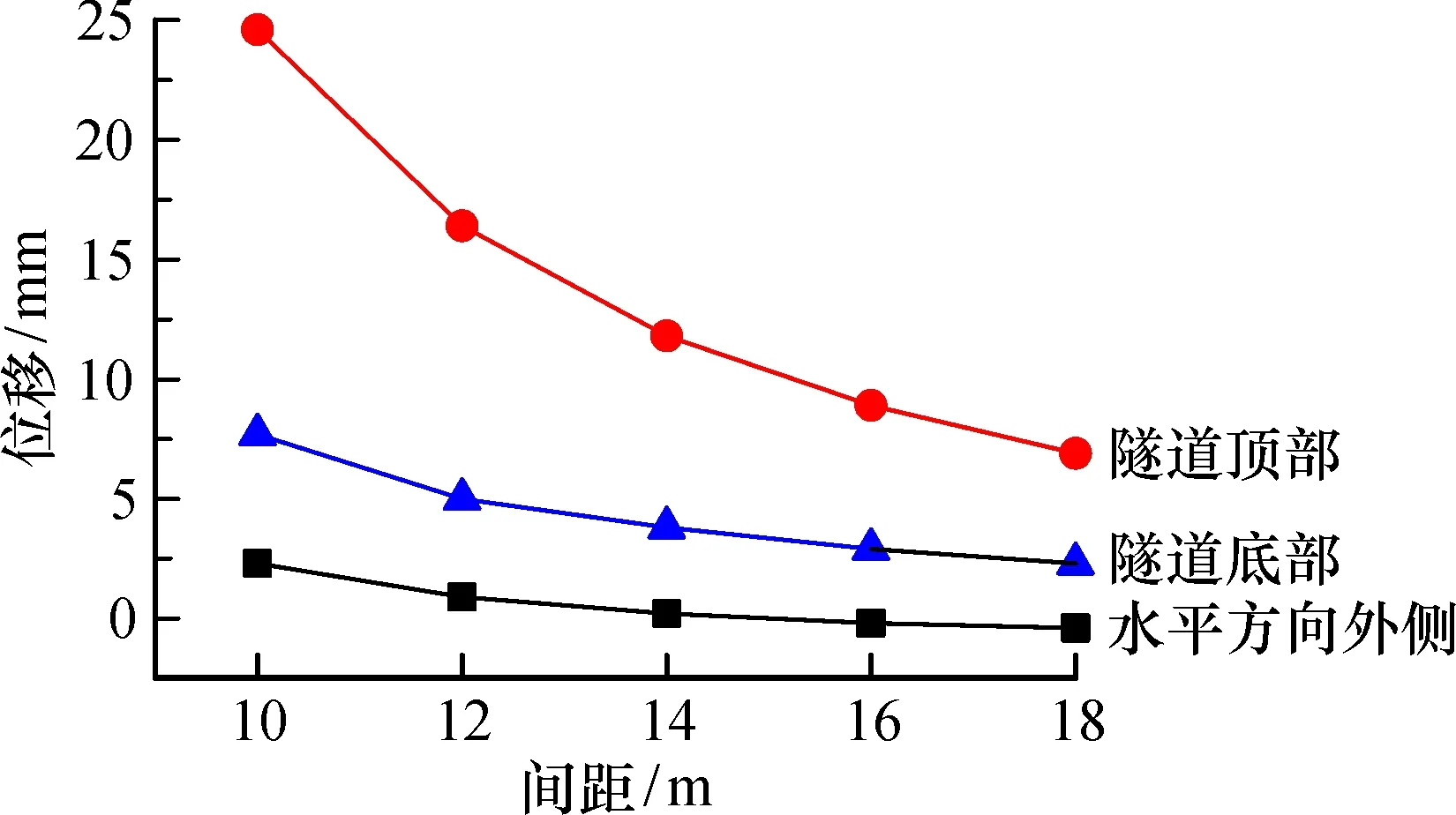
图16 隧道位移增量变化规律Fig.16 Variation of tunnel displacement increment

4 结论与建议

通过数值模拟软件FLAC3D分析了岩溶区溶洞对分离式隧道围岩应力与变形的变化规律,得到如下结论：

(1)溶洞会对分离式隧道顶部、底部围岩的应力及变形产生较大影响，溶洞对隧道顶部位移增长量的影响最大，其次是隧道底部和水平方向外侧。由于溶洞降低了围岩的实际厚度，随着隧道间距的增加，隧道围岩的应力增量出现明显下降，并最终趋向于无溶洞状态。

(2)在隧道间距为1倍开挖断面宽度(即12 m), 当隧道附近有溶洞时, 洞壁处的拉应力增幅大, 顶部最大拉应力由36.9 kPa增加到60.7 kPa, 增幅64.5%, 底部由6.8 kPa增加到28.2 kPa, 增幅314.7%, 即拉应力最大值多分布在隧道顶部, 但底部增长快; 洞壁处的最大压应力由221.2 kPa增加到257.4 kPa, 增幅为16.4%, 围岩的最大压应力由400.6 kPa增长到了440.2 kPa, 增幅为9.9%, 即压应力增幅不大, 且最大值分布在隧道之间而非洞壁处; 围岩的剪应力均有所增加, 溶洞厚度变小处其剪应力增长量远大于其他部位。

(3)对于围岩的拉应力而言，拉应力的增量随着隧道间距的增加而逐渐减小。当分离式隧道距离较近的时候，顶部的拉应力增长量要大于底部，但是当隧道间距达到约1.3倍隧道开挖断面宽度的时候，顶部和底部的增量就趋于一致；达到1.5倍开挖断面时，拉应力增量近似为零。

(4)对于围岩的压应力而言，压应力的增量随着隧道间距的增加而先增后减。当隧道间距约为隧道开挖断面宽度的83%时，围岩的最大压应力不但没有增加，反而略有减小；当隧道间距为开挖断面距离约1.17倍时，围岩最大压应力的增长率约为30.4%；当间距为1.5倍时的增长率为21.8%。

(5)对于围岩的位移而言, 围岩的位移量随着隧道间距的增加而逐渐降低。 隧道间距为隧道开挖断面宽度的83%时, 隧道位移增长率最大, 约为23.2%； 当开挖到1.5倍隧道开挖断面宽度时, 为6.9%。由于隧道围岩顶部拉应力大于底部拉应力, 故其顶部的位移增量大于底部的位移增量。

在本文模拟中，围岩质量为一类围岩，所使 用的岩石物理力学参数较大；同时，隧道模型为 浅埋型，荷载仅考虑岩体自重应力，荷载值较小。 因此，模拟计算所得到的各种应力与位移值较小。可能会与实际工程中的围岩类型、岩石的物理力 学参数以及所受荷载有一定差异。此外，本文也并未考虑隧道和溶洞大小、隧道形状、溶洞形状和数量变化等对分离式隧道的影响，这些都有待于今后作进一步的研究。