一种基于评价指标体系的优化TSP模型在多日旅行规划中的应用

刘长迎,高远昕,汤恬恬,杨 柳

(南京信息工程大学 a.数学与统计学院; b.大气科学学院;c.应用气象学院,南京 210044)

0 引 言

随着生活水平的提高, 人们对旅游的热情持续增长, 优良的旅行规划不仅安排合理， 使旅行者观感舒适, 还能降低旅行社成本、 提高效益[1]。 目前, 绝大多数旅行电商平台仍采用给定起始点的单日路线规划方案, 忽视了游客作息和不同景点观赏时间的问题，缺乏合理性和实际意义, 多日旅行规划成为各大旅行电商平台亟待优化的热门问题。 为解决该问题, 现阶段主要采用改进后的TSP模型进行多日旅行规划: 文献[2]以福州为例, 提出了一种基于时间框架的多日游行程优化方法; 文献[3]给出了一种基于兴趣点与旅行效益值的多日行程规划方式， 但由于此类模型不能根据实况灵活调整, 筛选出的最优方案常常不具时效性。

为此,本文采用一种“虚拟点”的实施策略,运用基于熵权法的TOPSIS分级模型对基于旅行效率和舒适度的游客体验感评价指标体系进行打分,进而优化TSP模型在多日旅行规划中的应用。改进的TSP模型可以灵活安排作息时间,亦可设置拓展端口接入实时路况、路线费用等,提高了实用价值。

1 问题描述与分析

对于旅行线路的规划,传统方法多将其转换为基于时间或路程的旅行商问题(TSP)进行求解,得到一条不间断的“路线环”。 而对于多日旅行规划, 考虑到入住地的频繁更换对旅行者十分不便,若假设每日入住同一地点(即每日旅行路线的起止点相同), 该问题便可转换为:设置“虚拟点”将由传统TSP模型所生成的“原始路线环”断开为多段路线链, 每一段路线链对应一日的旅行规划， 其难点在于如何设置“虚拟点”。 为此，建立基于旅行效率和舒适度的游客体验感评价指标体系, 运用基于熵权法的TOPSIS分级模型, 对“虚拟点”的设置进行评价, 得到最优解。

2 模型构建

2.1 生成“原始路线环”集

出行常用的5种交通方式:地铁、公交、自驾、骑行、步行,设以上交通方式的平均速度分别为a、b、c、d、e;景点i到j(i,j=1,2…,N)有K种交通工具组合方式,假设第k(k=1,2,…,K)种组合下5种交通方式的里程分别为Aij、Bij、Cij、Dij、Eij,则该种组合总耗时为

(1)

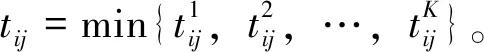
将该问题转化成一个关于时间的TSP问题[4-6]:构建无向图G1,将每个景点视为一个点,构成顶点集V1={v1,v2,…,vN},其中N为计划游览景点数;任意两个景点交通耗时构造为一条边,构成边集E1={eij,i,j,…,N,i≠j};每条边eij赋以权重tij，即交通耗时。假设2个景点的旅行顺序对交通耗时没有影响,则tij=tji,故图G1是无向图,其权矩阵也是对称的。

采用蚁群算法[7-8]求解该TSP问题。由于该算法存在不稳定性,为了尽可能寻找最优解,在利用该算法进行多次求解后,滤去结果中超过当前次数中最优结果20%的解,得到路线环共计L个,称为“原始路线环”集。

2.2 设置虚拟点

对路线的多日规划,相当于将1个“原始路线环”截断为多段, 每段对应一日的旅行路线, 对此引入“虚拟点”进行截断操作。“虚拟点”的设置流程图如图1所示。

图1 虚拟点设置流程Fig.1 Flow chart of virtual point setting method

①选定景点Ji(i=1,2,…,N)作为首日的起始景点,称为首日虚拟点;②沿着原始路线环,根据各景点的游玩时间、景点之间的交通耗时,在景区开放时间T的限制范围内,确定该日的最后一个景点;③得到每日的虚拟点(如第2日首个景点为“第2日虚拟点”),重复步骤②,直至完成所有景点的游览;④遍历N个景点作为首日虚拟点,共得到N×L种虚拟点的设置方案。

可见,在确定首日虚拟点后,沿原始路线环顺时针或逆时针进行游览会得到不同结果,故实际将产生2N×L种虚拟点的设置方案。根据实际情况,可适当拓展虚拟点的设置规则②,对游览时间、交通耗时等进行修正。本文以修正交通耗时为例，引入交通拥堵系数，设工作日早、晚高峰平均道路拥堵系数分别为a1、a2,周末早、晚高峰平均道路拥堵系数分别为b1、b2，此时,若旅行者于工作日早高峰从景点i前往景点j,则修正后的交通耗时tij′=a1×tij。

2.3 游客体验感指标体系的建立[9]

为了寻找最优的方案,本文基于旅行时间与舒适度,建立如下指标体系对虚拟点生成的2N×L种方案进行寻优。

2.3.1 旅行效率影响指标 1)交通时间σ1。理想的旅行方案应当在交通上花费的时间更少。

(2)

2)等待时间σ2。 若旅行者在景区开放前到达, 则等待开放的时间将被视为一种损耗。

(3)

2.3.2 舒适度影响指标 1)旅行灵活度σ3。旅行中存在突发状况,故旅行者某日在游览完最后一个景点时距离景点关闭时间越长,就有更高的灵活度。

(4)

2)交通拥挤度σ4。早晚交通高峰造成的堵车会大大降低旅行舒适度。

(5)

3)景点疲惫度σ5。 若旅行者在某天游览景点数大于日平均, 记pi=1； 否则，记pi=0。

(6)

综上,游客体验感评价指标体系如图2所示。

图2 游客体验感评价指标体系Fig.2 Tourist experience evaluation index system

2.4 基于熵权法的TOPSIS评价模型的建立

2.4.1 数据预处理 对虚拟点生成的2N×L种方案对应的5个指标构建原始矩阵X2NL×3, 并进行趋同化处理, 将低优指标转化成高优指标， 再将数据标准化, 得到标准化矩阵Z2NL×5。

(7)

2.4.2 熵权法确定权重 熵权法是指在进行指标评价的过程中,根据各指标的差异程度确定权重的一种客观赋权方法,主要通过熵值的大小来度量该指标值所提供的信息量的有效程度[10-11]。确定权重步骤如下:对于标准化数据矩阵Z,首先计算第j个指标下第i个评价对象的指标值的比重pij

(8)

再计算第j个指标的熵值ej

(9)

其中,k=1/ln(2NL), 最终得出第j个指标对应的熵权wj

(10)

2.4.3 TOPSIS法进行评价 TOPSIS法是根据有限个评价对象与理想化目标的接近程度进行排序的方法,是在现有的对象中进行相对优劣的评价[12-13]。它将各对象的评价指标值组成一个空间,通过计算空间中各点与正负理想解的距离得到与正理想解的接近程度,从而对评价对象进行定量排序。具体步骤如下:

1)计算与正负理想解的距离。据标准化数据矩阵Z,得到最优向量Z+(正理想解)和最劣向量Z-(负理想解)

(11)

(12)

其中,wj为第j个指标的权重, 由熵权法得到。

3)计算与最优解的接近程度。 根据以上各对象和最优向量与最劣向量的距离, 计算各方案与理想最优解的接近程度εi

(13)

其中： 0≤εi≤1,εi→1表明评价对象越优。

4)据εi的大小对虚拟点所生成的方案进行综合排序,εi越大,表明该虚拟点设置方案越优。

3 算例分析

3.1 算例求解

根据建立的基于评价指标体系的优化TSP模型,对南京旅游年卡覆盖的市区24个景点进行多日旅行线路规划。

3.1.1 构建原始路线环集并生成虚拟点 24个景点已由表1列出并编号(N=24), 同时将旅行者住所定于交通枢纽南京站附近。 运用百度地图相关数据, 根据式(1)得到每两个景点及每个景点到南京站的最短交通用时,与景点官网的建议旅行时间一并代入2.1节模型,得到L=5条原始路线环,如表2所示。

表1 旅游景点及编号Table 1 Tourist attractions and numbers

表2 原始路线环集Table 2 Original alignment ring set

通过数据调查,交通早高峰时段为7:00—9:00,晚高峰时段为17:00—19:00。 本文沿用2019年8月19—25日为期一周的南京早晚高峰拥堵情况,得到工作日早晚高峰平均拥堵系数a1=a2=1.656,周末早晚高峰平均拥堵系数b1=1.135,b2=1.365。再通过2.2节模型,得到240种虚拟点的设置方案。

表3 旅行线路相关指标Table 3 Travel routes and relevant indicators

图3 最优旅行方案线路图Fig.3 Route map of optimal travel scheme

3.2 结果对比

为了验证本文模型在解决多日旅行规划问题上的优越性, 将得到的最优旅行路线与百度地图生成的最优路线进行对比。根据优化景点数的不同,共进行5组实验,得到各路线的εi值,从而得到优化模型和软件生成方案的平均εi及评分对比结果(图4)。 从不同旅行景点数限制下路线评分对比可知,本文提出的优化路线评分值高于地图软件生成的最优路线,且随着景点数的增多,评分增幅有显著提升，表明本文模型得到的路线结果相较于现行算法更为优质,能更加高效地解决旅行景点数较多情况下的多日行程规划问题。

图4 最优路线方案结果对比Fig.4 Comparison of optimal route results

3.3 模型稳定度分析

绘制以5条原始路线环分类的240种方案评分箱线图(图5)。

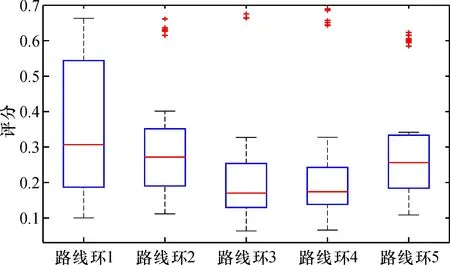
图5 以5条原始路线环分类的方案评分箱线图Fig.5 Box diagram of scheme score classified by 5 original routes

组内来看,红十字点被视为“离群点”而处于内限之外, 说明这些数据点相较于数据群体非常“出类拔萃”，即本文所建立的评价模型能有效区分方案的优劣, 筛选出来的最优方案具有绝对的优势。组间来看,该评价模型对第2～4条原始路线环中虚拟点设置方案优劣度的区分性很强,对第1条原始路线环区分度较强,且每组最优解的评分很接近，在一定程度上弥补了因蚁群算法的不稳定性而造成在求解TSP模型时可能引起的方案漏选,大大增强了模型整体的稳定度。

4 结果与讨论

通过引入“虚拟点”概念,对传统TSP模型在多日旅行规划中的应用进行了优化,并从旅行效率及舒适度两方面建立了指标体系,运用基于熵权法的TOPSIS评价模型确定出最优方案。通过实例验证发现，本文提出的基于指标体系的优化TSP模型相较于现有算法,在解决多日旅行规划时能够获得质量更优的解。但研究还存在不足,尚有旅行费用及住宿问题未得到充分考虑,将来可以通过文中提及的拓展端口对模型进行修正,进一步提升实用性及稳定性。