基于萤火虫属性约简的教学质量评价

（阜阳师范大学信息工程学院，安徽 阜阳 236041）

1 引言

近年来，高校竞争日趋激烈，教师的教学质量对高校的发展具有重要意义，直接关系到学生对知识的掌握以及学生能力的培养。教授教学质量评价是参照一点教学目标，通过对教学相关信息的搜集、分析，利用科学有效的手段，对教学过程，教授结果进行价值判断。客观、公正的教师教学质量评价体系能够检测教师的教学效果，促进教师发现教学中的问题，提高教学质量水平[1-3]。然而，现有的教学质量评价指标繁冗复杂，使得对教师教学质量进行评价打分的工作量较大[4]。事实上，有些评价指标并非是必不可少的，其对评价结果影响较小甚至没有影响，这部分评价指标可以称为是冗余指标，其他的评价指标可以称为是必要指标。冗余的评价指标是使得教师教学质量评价的工作量加大的主要因素，如何在不影响评价结果的前提下对冗余指标进行剔除，只保留必要指标，对简化教师教学质量评价体系具有重要意义。

人为地剔除冗余教学质量评价指标，受主观因素影响较大，缺乏科学性。目前，已有学者根据粗糙集理论[5]，将属性约简用于教学质量评价系统中[6,7]，该方法可以排除主观因素的干扰，让数据自己说话，客观地简化教学质量评价体系。文献[6]利用粒度计算理论实现教学质量评价指标的约简，保留必要指标，删除冗余指标，简化教学评价系统。文献[7]利用条件信息商对教师教学质量的评价指标进行约简，删除冗余指标，从而优化教学评价系统。这些方法均是利用粗糙集理论进行属性约简，然而，粗糙集属性约简的复杂度较高（O（nn））。为了解决这以难题，本文利用群智能方法实现教学质量评价系统的属性约简。

群智能方法有蚁群算法[8]、人工蜂群算法[9]、人工鱼群算法[10]、以及萤火虫算法[11]等。其中，萤火虫算法涉及的参数较少，收敛速度较快，操作简单，常被用于解决各种优化问题。由于萤火虫优化算法通常是解决连续性问题，而属性约简实质上是一个0-1规划的组合优化问题，可采用改进的萤火虫优化算法，即二元萤火虫优化算法进行属性约简的求解。目前，二元萤火虫算法已被用于参数集成剪枝、属性选择都问题，并且得出较优的效果。因此，本文采用二元萤火虫优化算法解决教学质量评价的属性约简问题。

2 相关介绍

2.1 属性约简

属性约简是粗糙集理论的一个重要内容，设信息系统 S=（U,A=CUD,V,f），，其中，非空集合 U为论域，集合C为条件属性集，集合D为决策属性集， 集合V=｛Va|a∈ A ｝，Va为属性a的值域，函数 f=｛fa:U×a→Va ｝为信息函数[5]，当D非空时，S=（U,A=CUD,V,f）即为决策系统。

定义1给定一个决策系统S=（U,A=CUD,V,f），B，则称

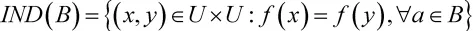
为U上关于B的等价关系，由它可确定U的一个划分，记作U／IND（B）。 给定 X，RA，则R－（X）＝U｛ Y∈U／IND（R），YIX ≠｝称为X关于R 的上近似，R－（X）＝U｛ Y∈U／IND（R），YX｝称为关于的下近似。

2.2 萤火虫算法

Krishnanad等人[11]于2005年提出萤火虫优化算法（Glowworm Swarm Optimization,GSO），该算法是一种仿生启发式算法，其主要思想是，每只萤火虫在其视线范围内，向亮度较高（即是荧光素较大）的萤火虫移动，通过不断迭代，最终获得最优萤火虫，也即是最优解。GSO算法主要分为如下三个更新阶段来寻求最优解。

（1）更新荧光素：

其中，li（t）为第i个萤火虫在t时刻的萤火素，J为适应度函数，xi（t）为为第 i个萤火虫在 t时刻的位置，ρ为荧光素挥发系数，γ为荧光素增强系数；

（2） 更新位置：

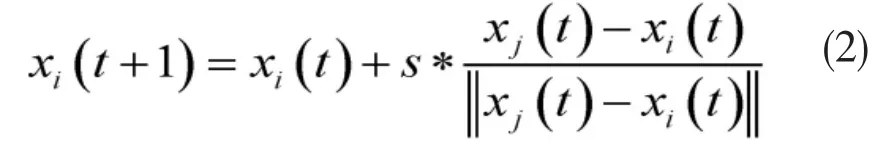
其中，xj（t）为 t时刻第 j个萤火虫的位置，且此时第j个萤火虫的亮度高于个i萤火虫，s为移动步长。若此时在第i个萤火虫的决策半径内，比其亮度高的萤火虫有多个，并且这些萤火虫构成一个集合Ni（t），此时根据转移概率的值，将第i个萤火虫的移动向转移概率最大的萤火虫移动。转移概率计算如下

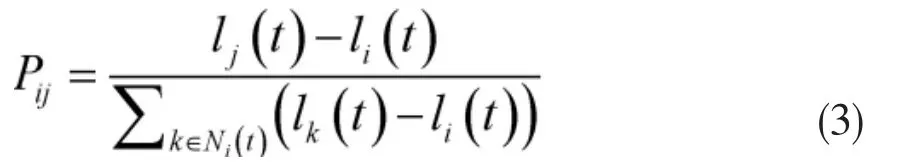
（3）更新决策半径

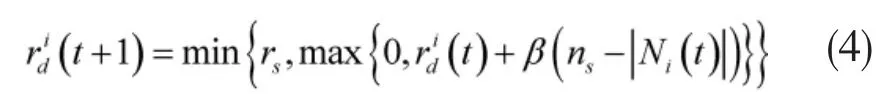
其中，rs为感知半径，ns为领域萤火虫个数阈值，β为领域变化率。

因教学质量评价属性约间问题，实际上就是教学影响因素预测问题，因此是一个二元离散优化问题，每个教学质量影响因素只有两种状态，分别是必要因素（用“1”表示）或冗余因素（用“0”表示），故本文使用二元萤火虫算法[12]。具体为，设教学质量评价影响因素共有个，则时刻，第个萤火虫的位置可表示为 xi（t）＝（xi1（t），xi2（t），L，xiL（t）），则在位置更新阶段，采用如下公式进行更新

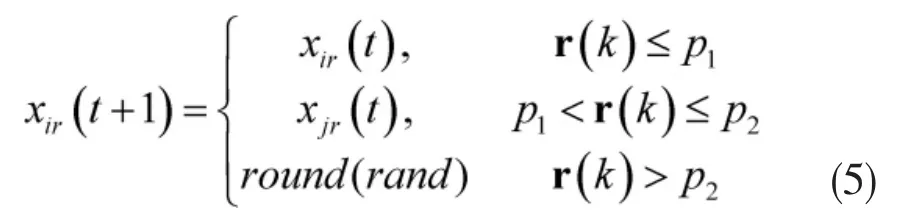
其中，r为0到1的随机维变量，P1和P2为位置更新参数。

3 基于萤火虫属性约简的教学质量评价

3.1 基于二元萤火虫算法的教学质量评价属性约简

假设教学质量评价系统的评价指标个数为L，构成的属性集记为C，教学评价结果作为决策属性记为D。为了较小评价系统的复杂度，本文通过属性约简最大化的剔除冗余指标。因此，本文在利用二元萤火虫算法对教学质量评价系统进行属性约间时，将萤火虫个体当前位置中各个分量中值为1的个数作为适应度函数值，例如，设 xi（t）＝（1，0，0，0，1，0，1，1），则适应度函数 J（xi（t））＝4，此时，xi（t）对应的属性集记为 Si（t）表示只保留了所有属性中第1、5、7及 8这四个属性，。

基于二元萤火虫算法的教学质量评价属性约简算法步骤如下：

步骤1利用Tent混沌序列对萤火虫种群中各个体位置进行初始化，并初始化相关参数rs，ns，ρ，γ，p1，p2，β，li（0），以及最大迭代次数，t_max，设置 t＝0；

步骤2对于所有的萤火虫个体，若有POSSi（t）（D）≠POSC（D）则对该萤火虫重新分配位置；

步骤3计算萤火虫个体的适应度函数值J（xi（t））， 记满足 POSSi（t）（D）＝POSC且对应的 J（xi（t））最小的个体位置记为optimum；

步骤4按照公式 (1)计算萤火虫个体的应该素，在萤火虫个体的决策半径内，找到所有满足 POSSj（D）＝POSC（D）且荧光素较高的个体 j作为自己的邻域集 Ni（t）；

步骤 5 根据公式(3)计算转移概率 Pij（t），并选择Pij（t）的最大值所对应的萤火虫个体j；

步骤6根据公式(5)更新各萤火虫个体的位置，对某个萤火虫个体 j，若 POSSj（D）≠POSC（D），则对其进行高斯变异策略；并根据公式(4)对萤火虫的决策半径进行更新；

步骤7计算萤火虫个体的适应度函数值J（xi（t）），记满足 POSSj（t）（D）＝POSC（D）且对应的 J（xi（t））最小的个体位置记为 opt，若 J（opt）〈J（optimum），则 optimum＝opt；

步骤 8 令 t＝t＋1；

步骤9循环步骤4～步骤8，直到达到最高迭代次数t_max，输出optimum，算法终止。

3.2 基于萤火虫属性约简的教学质量评价

以文献[6]中某校教学质量评价系统为例，将教学质量评价的15个影响因素（包括选用教材、教学准备、使用现代教学、普通话教学、课堂组织、书写表达、教师教学、讲授方法、教师教学、讲授过程、课堂信息量、运用启发式教学、教学目的、教学深度以及课堂时间安排等）作为条件属性，把授课教师的最终得分作为决策属性从而构成决策系统，利用本文所提方法对该决策系统进行属性约简。最终得出只含有3个条件属性的决策系统，剔除了12个冗余的条件属性，结果如表1所示。

从表1可知，教学深度、运用启发式教学以及课堂组织这三个属性可看作是影响教学质量评价的必要因素，而其余12个因素可看作教学质量评价的冗余影响因素。因此，在以后的教学质量评价中，可对教学评价系统进行简化，剔除冗余影响因素。

表1 属性约简结果表

4 结束语

本文提出基于萤火虫属性约简的教学质量评价方法，通过利用萤火虫寻优方法对教学质量评价系统进行属性约简，鉴于属性约简实质上是一个0-1规划的组合优化问题，而萤火虫优化算法通常是解决连续性问题，因此，本文采用二元萤火虫算法对教学质量评价体系进行属性约简，从而剔除教学质量评价的冗余影响因素。通过对某校的教学质量评价数据进行实验，表明本文方法可对教学评价系统中的冗余指标进行约简并保留必要指标。因此，本文所提方法可以有效简化教学质量评价体系，对教学质量评价的高效实施提供理论价值。