利用投影变换的平面度误差评定

孙 烁，赵凤霞，辛传福，张琳娜

（郑州大学机械工程学院，河南 郑州 450001）

1 引言

平面常作产品设计、加工、装配和检测的基准，平面度误差对产品的性能有着重要的影响，因此快速准确地评定平面度误差具有重要的意义。评定平面度误差的方法有最小二乘法、对角线平面法、三远点平面法和最小包容区域法。其中，最小包容区域法[1]是平面度误差缺省评定方法。常用的最小包容区域评定法有：变换作图法、旋转变换法、变换计算法、极点计算法、计算几何法等，这些算法不适合进行几何误差的数字化评定，与现代化的测量设备不相适应。近来出现比较有代表性的算法有凸包法[2]、新型凸包法[3]。凸包法是基于凸壳理论提出的计算几何法的一种，通过空间点集进行计算，具有结果唯一、理论明确的特点，但同时也存在着不足，一些学者提出了改进新型凸包法。随着智能算法的出现，有些学者将遗传算法，粒子群算法和蜂群算法等也逐渐运用在平面度误差的评定中。近几年又有了几何搜索逼近算法[4]、改进遗传算法[5]、改进粒子群算法（PSO）[6]、改进人工蜂群算法（MABC）[7]、模拟植物生长算法[8]（PGSA）、差分进化算法[9]和进化策略算法[10]等。其中，几何搜索逼近算法不断地对基准点进行比较、估计和变换，构造新的辅助点、参考面和辅助面，最终实现平面度误差的最小区域评定。基于实数编码的改进遗传算法，提高了收敛速度，具有较强的稳定性和较高的精度。PSO 增加粒子的多样性，解决了局部最优的问题，加快了收敛速度。MABC 在原算法基础上引入两牵引蜜蜂和禁忌搜索策略。模拟植物生长算法（PGSA）是一种新的智能算法，具有较强的全局优化特性。根据平面度误差的定义和几何特征，提出一种利用投影变换的平面度误差评定方法，并用该方法代替平面度误差的最小包容区域评定。

2 平面度误差的投影变换评定原理

AX+BY+CZ+D=0 是平面在空间直角坐标系中的一般方程。式中：n（A，B，C）是平面的法向量；D 是一个常数，它确定了平面的位置。由平面度的定义可知，最小区域平面度误差值为用两理想平行平面（即评定基面）包容提取（实际）平面时所具有的最小宽度值，因此，理想平面的位置（即D 值）不影响平面度误差值的大小。

由平面的法向量定义和性质可知，将评定基面和所有测量点向评定基面的某一法平面上进行正交投影，两平行平面投影后的距离不变，且投影得到的两平行直线包容所有测量点。由此即可将平面度的最小包容问题转化为给定平面内的直线度的最小包容问题，如图1 所示。

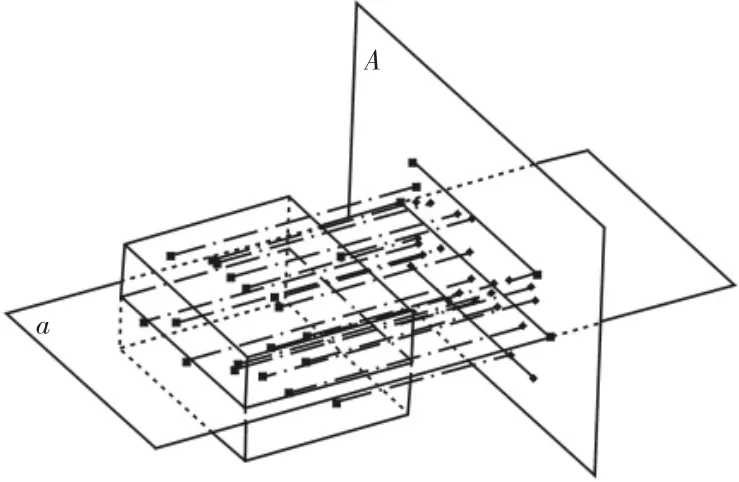
图1 投影变换原理图Fig.1 Projection Transformation Schematic Diagram

该方法的关键之处在于如何寻找到最优的法平面。对任何一个理想平面来说，都能找到无数个法平面，不同的法平面上，其对应的投影后的测量点的密度不一样。投影在法平面上的点越密集，那么影响平面度误差评定的其他因素就越少，平面度误差评定的结果也就越准确。通过实例验证发现，当把测量点投影在包含基面短边的法平面上时，投影后的测量点的密集性最好，因此，选择包含基面短边的法平面作为最优法平面。

3 平面度误差的投影变换评定过程

利用投影变换法的平面度误差评定过程为：首先采用最小二乘法对原始测量点进行拟合，得到一个初始参考基面（最小二乘拟合平面），寻找初始参考基面的短边并构造法平面，然后将初始参考基面与原始测量点全部投影到法平面上，在法平面内进行平面直线度误差的最小区域评定。由于直线度误差评定基面与平面度误差评定基面不同，因此，最后还需进行倾斜校正才能得到最小包容区域平面度误差值。

3.1 构建最小二乘参考基面

假设测量点坐标是：

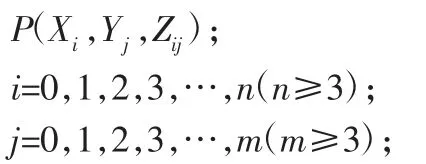
其最小二乘拟合参考平面方程可写成：

式中：p，q，c—最小二乘中心平面的方程系数，根据各测得点的坐标值，按照式（2）～式（4）可得；n—X 方向的分段数；m—Y 方向的分段数。

3.2 寻找最优法平面

A，B，C，D 是参考基面上的四个顶点，如图2 所示。根据式（5）和式（6）计算出AB和BC的长度。比较AB和BC的长度，找到较短的边。

假设BC 边为短边，构建过基面BC 边的法平面（M2）。根据立体几何可知，两个不共线的向量确定一个唯一的平面。参考基面的法向量是法平面上的一个向量。那么n1，n2是法平面里的两个不共线的向量，n3是法平面的法向量。n1，n2，n3可以通过式（7）～式（9）进行计算。

法平面（M2）可以通过式（10）计算求得：

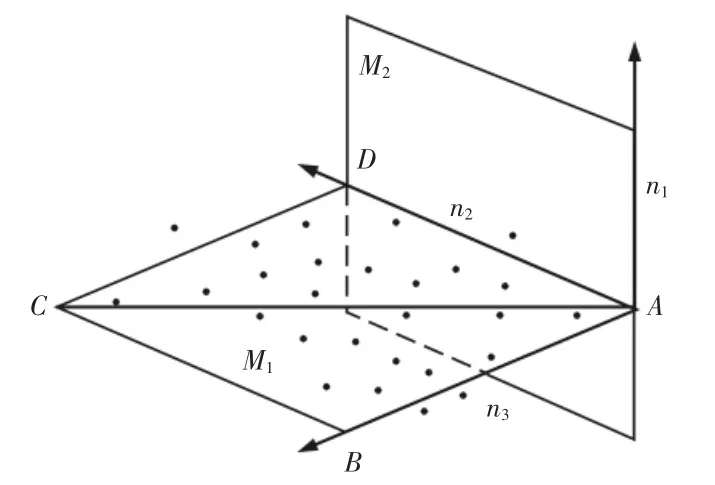
图2 构建最优法平面Fig.2 Construction of the Optimal Normal Plane

3.3 投影变换

将所有的测量点（P（Xi，Yi，Zij））投影在法平面（M2）上，投影后的测量点坐标P1（xi，yj，zij）由以下步骤获得，如图3 所示。这里以一个测量点P（XP，YP，ZP）为例说明投影变换的具体过程。其中，P1（xP，yP，zP）是该点投影后的坐标。

根据P1点满足法平面方程可得：

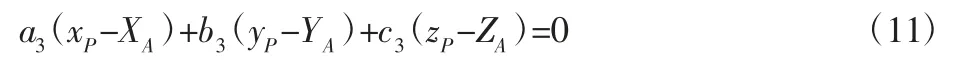
由PP1 和n3平行可得：

上述公式变换可得：

将式（13）和式（14）带入式（11）中可得xP：

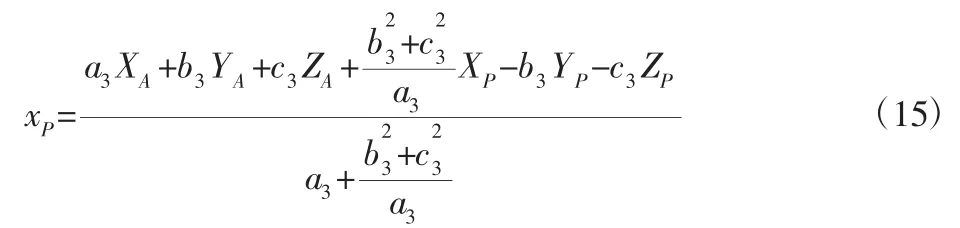
把式（15）带入到式（13）和式（14）中可以得到 yP和 zP的值。所有测量点投影后的坐标都可以根据上述步骤得到。

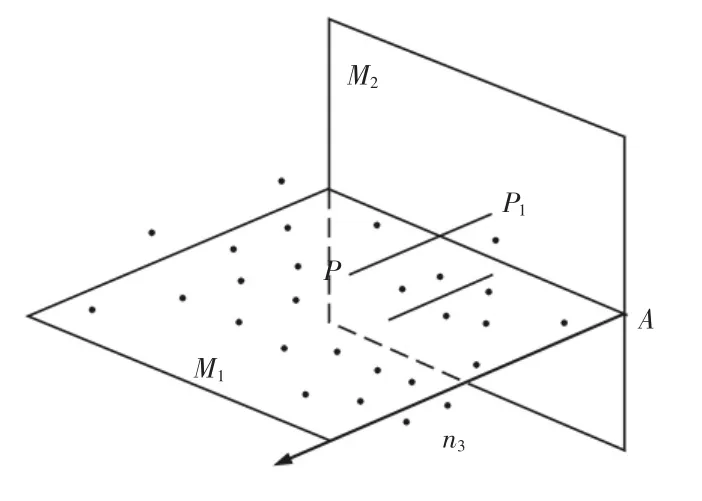
图3 投影变换Fig.3 Projection Transform

3.4 评定最小区域直线度误差

投影变换后的法平面的正视图，如图4 所示。平面度的最小包容问题已转化为给定平面内的直线度的最小包容问题求解。

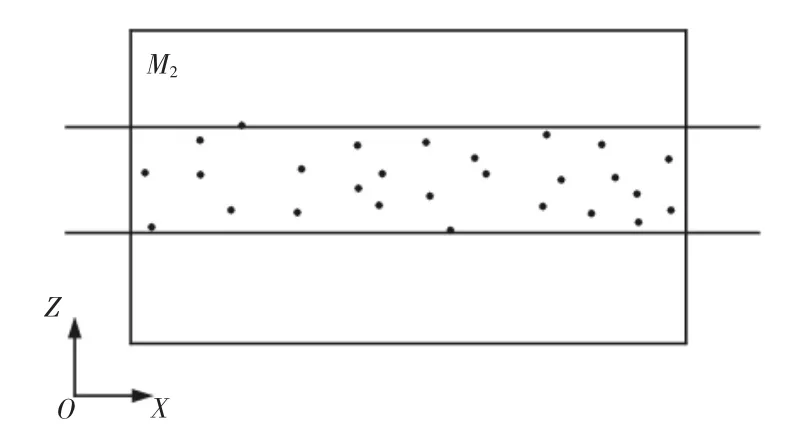
图4 法平面的正视图Fig.4 The Orthographic View of the Optimal Normal Plane

3.5 倾斜校正

投影变换操作后的点坐标是在全局坐标系下得到的，而在3.4 章节中叙述的直线度误差评定时应使用的是法平面的局部坐标系下的点的坐标。因此，必须将投影后点的坐标由全局坐标系下转换成局部坐标系。假设误差值线段为L1，而真实的误差值线段（平面度误差）为L，如图5 所示。经过倾斜校正操作将L1转变为L。

L1和L 之间的位置关系如下：

式中：θ—线段 L1和 L 之间的夹角，也是法平面（M2）和 XOZ 平面（或YOZ 平面）之间的夹角。法平面的法向量是n3，XOZ 平面的法平面是n4。

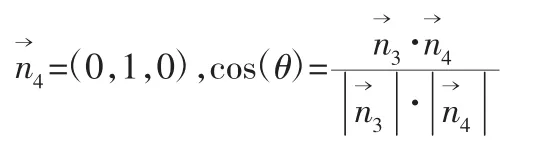
平面度误差值w0的计算公式如下：

注：YOZ 平面的法向量为（1，0，0）。

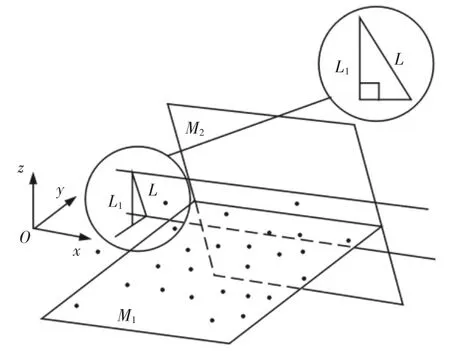
图5 倾斜校正Fig.5 Tilt Correction

4 实验验证

在MATLAB R2014a 环境下，按照前述步骤进行编程实现该算法。实验数据来源与其评定结果，如表1 所示。第1 组数据在MATLAB 中的运行结果示例图，如图6 所示。

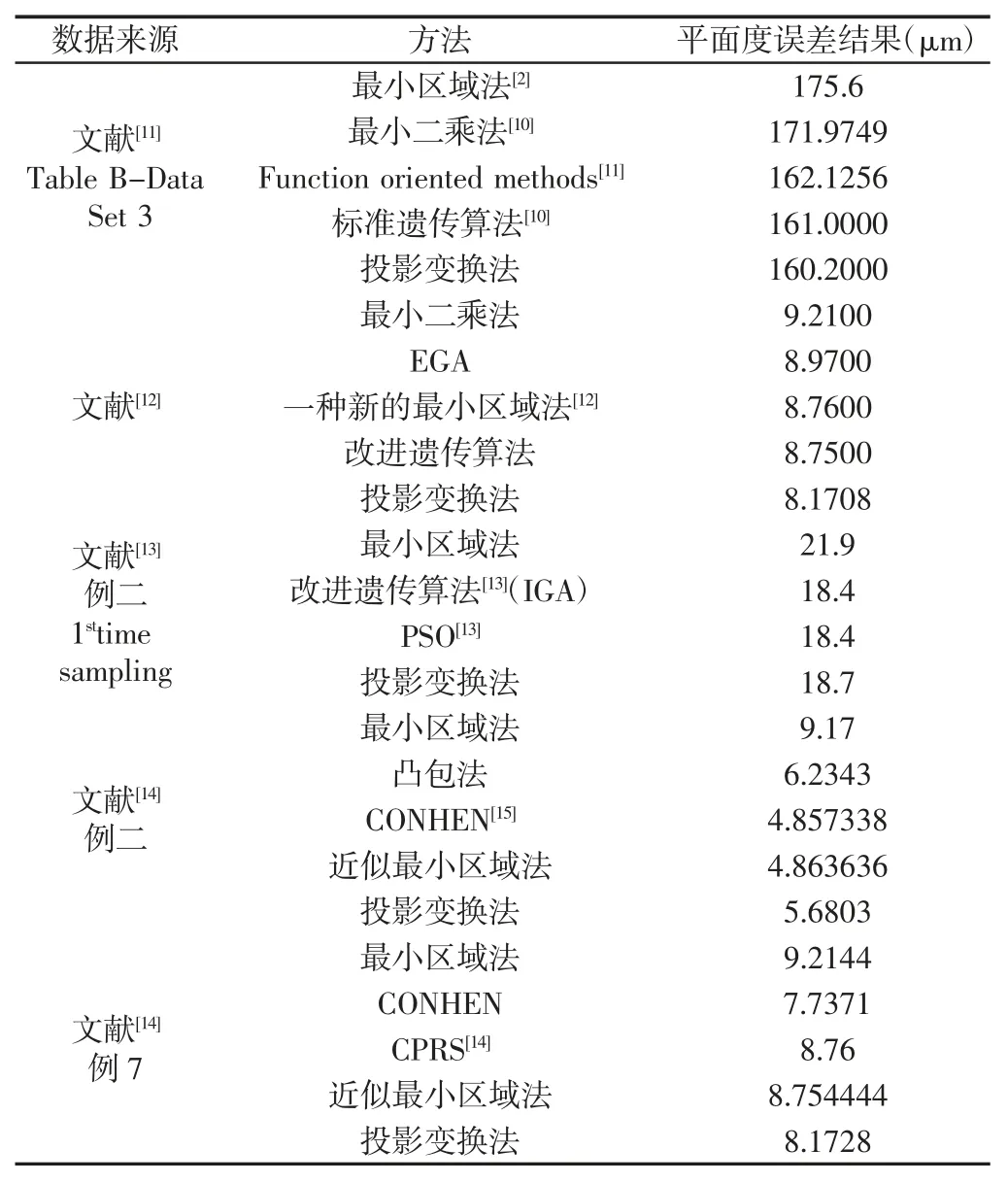
表1 不同方法的平面度误差结果比较Tab.1 Comparison of Flatness Error Results Obtained by Different Methods

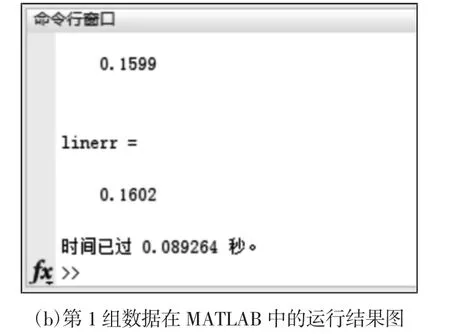
图6 第1 组数据在MATLAB 中的运行实例图及结果图Fig.6 The First Group of Data in MATLAB Operation Example Diagram and Results Diagram

表1 给出了不同方法的平面度误差评定结果。其中前4 组数据测量点为25 个，第5 组数据测量点为70 个。

在第1 组数据中，提出的投影变换法的计算结果为160.2（μm），计算时间大约为0.10s。该结果与标准遗传算法有着很好的一致性，明显优于最小区域法，最小二乘法，Function oriented methods 等方法。第2 组数据的结论与第1 组相同。第3 组数据中IGA 算法需要大约70 次迭代才能找到最优解，而提出的方法不需要设置参数和繁琐的迭代过程，可以达到类似于IGA 的计算结果，计算时间约为0.15s。

文献[14]提出了一种近似最小区域的方法。通过对其中的示例2 和7 的数据进行了处理分析可知：近似最小区域法和投影变换法在优化程度上略逊于CONHEN 法。例7 中的测量点数据比较多，其包含的平面度误差信息更多，精度也较高。在例7 中，投影变换法的结果与CONHEN 法的结果之差为0.4347（μm），而在例2 中，两者算法结果之差为0.8229（μm）。由此，可以推断出，测量点越多，提出的投影变换法计算结果不仅优于近似最小区域法，而且在优化程度上也更接近于CONHEN 法。

综上所述，提出的平面度误差评定的投影变换法比近似最小区域法和CONHEN 法具有原理清晰、计算简便的优点，因此该方法为平面度误差的评定提供了一种全新的思路。

5 结论

利用投影变换的思路，提出一种新的平面度误差评定方法。应用不同文献中的多组测量数据，将投影变换法应用到平面度误差的评定当中，与不同文献中的多个方法进行比较，其结果表明：

（1）投影变换法的计算结果明显优于最小二乘法、最小区域法和凸包法，具有较强的稳定性和收敛性。

（2）投影变换法的结果与标准遗传算法和改进遗传算法有着很好的一致性，验证了该方法的正确性与可行性。在同组数据下，投影法的计算时间比前者大约缩短1s，比后者缩短0.06s，具有计算效率高的优点。

（3）在测量数据较多的情况下，投影变换法的结果优于近似最小区域法，并且在优化程度上也更加接近于CONHEN 法，比CONHEN 法的原理更加清晰、简单易懂。

该方法为评定平面度误差提供了一种全新的、切实可行的思路，也为其他的误差评定做出了参考。