CFRP 汽车防撞梁结构/材料一体化优化设计

臧 杰 ，周金宇 ，邱 睿

（1.江苏理工学院“结构/材料多尺度协同设计与制造”江苏省高校优秀科技创新团队，江苏 常州 213001；2.机械科学研究总院江苏分院有限公司，江苏 常州 213001）

1 引言

汽车防撞梁是汽车设计制造的关键部位，对其外在形状的设计和制造材料的选择直接影响到汽车的安全性与稳定性。碳纤维复合材料（CFRP）具有比强度高、比模量大、密度低等优异性能，使得它在防撞梁设计中有着广阔的应用前景[1]。与传统高碳钢、铝合金材料相比，CFRP 能够大幅度减轻汽车防撞梁的质量，同时提高其强度性能，这对防撞梁的安全与稳定具有重要意义。因此，对CFRP 汽车防撞梁的优化设计已成为一个研究热点。

针对复合材料汽车防撞梁的应用，国内外学者均已作出一定的研究。Renault 最早将片状模塑料（SMC）材料应用于汽车防撞梁，取代传统的金属防撞梁；文献[2]综合分析高碳钢、玻璃纤维、碳纤维三种防撞梁的耐撞性能，证明碳纤维耐撞性能最好且轻量化程度最高的结果；文献[3]针对铝合金、玻璃纤维及碳纤维三种防撞梁，从质量、比吸能与最大碰撞力等方面进行对比；文献[4]根据复合材料的结构特点和防撞梁碰撞工矿中的受力及约束情况，提出一种变截面厚度设计方法；文献[5]分析了CFRP 层合板的吸能特性，并以最小碰撞峰值力为目标，以碰撞器入侵量为约束对CFRP 层合板进行铺层角度优化。CFRP 汽车防撞梁与传统防撞梁相比，具有明显优势，这已在诸多文献中得到验证，而同时考虑结构与材料两个层面对防撞梁性能影响的研究仍属少数。

综合考虑结构与材料两个层面的变化对防撞梁整体性能造成的影响，实现结构/材料双尺度协同优化。在结构层面采用组合B 样条曲线对防撞梁的轮廓曲线进行参数化表达，并对防撞梁截面的关键尺寸调整，在材料层面对层合板选择不同的铺层角度方案，基于自适应遗传算法对B 样条轮廓曲线、截面关键参数与铺层角度进行多变量优化，确保防撞梁具有良好的强度性能。

2 结构参数化建模

2.1 B-Spline 轮廓曲线

B-Spline 曲线可以表达和设计自由型曲线，是当今形状数学描述的主流方法之一，兼备了Bezier 曲线的优点，包括几何不变性等，同时克服Bezier 曲线在阶次较大时对曲线控制减弱、不能做局部修改等缺点。设P0，P1，…，Pn为给定空间内n+1 个控制顶点，U=｛u0，u1，…，un+k+1｝是 n+k+1 个节点矢量，则 k 次 B-Spline曲线可以定义为：

式中：Ni，k（u）—k 次B-Spline 曲线的基函数，可定义为：

k=0 时：

k=1，2，…，n 时：

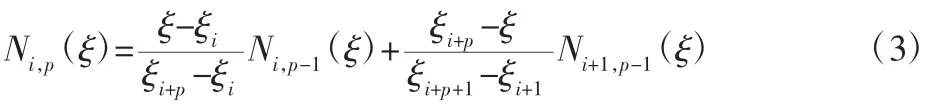
采用组合B-Spline 曲线对汽车防撞梁轮廓曲线进行拟合重构，如图1 所示。OA 段由直线构成，方便防撞梁与车身装配螺栓链接；AD 段曲线是由两个控制顶点B、C 控制的三次均匀B 样条曲线，用于连接底座与抗冲击面，起到缓冲作用；DG 段曲线由控制顶点E、F 控制的三次均匀B 样条拟合表示，用于承载冲击力。

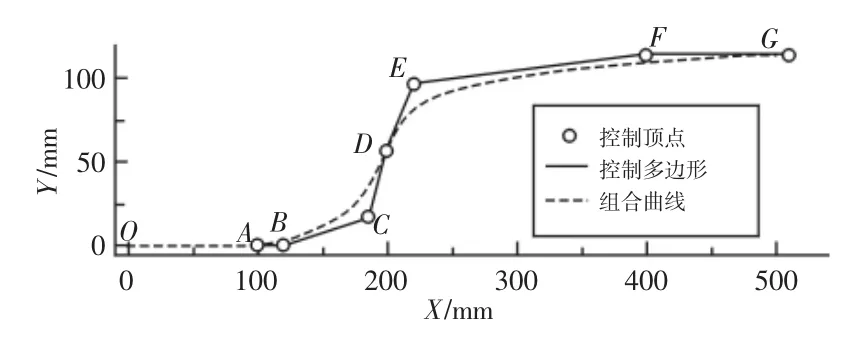
图1 组合B-Spline 轮廓曲线Fig.1 The Profile Curve of Combined B-Spline

对防撞梁结构的参数化表达，设计参数为关键控制点di。通过对于关键控制点B、C、E、F 坐标的变动，对曲线AD、曲线DG形状进行修改。为保证防撞梁表面圆滑，B-Spline 曲线在连接点处需要与其他线相切，即满足B 点Y 向坐标与A 点相一致，F 点Y 向坐标与G 点相一致，D 点坐标在直线CE 上。

2.2 有限元模型的建立

所用的某汽车防撞梁模型的几何形状与尺寸，如图2 所示。防撞梁A-A 截面上存在2 个设计参数，层合板厚度d 以及截面关键尺寸参数l。Ansys 几何建模过程中，将B-Spline 轮廓曲线的节点坐标以APDL 命令流的形式输入，并拟合成样条曲线，防撞梁模型是由截面沿样条曲线方向扫略而成。防撞梁属于薄壁零件，采用壳单元建模，其有限元模型，如图3 所示。整个建模环节，由Matlab 软件调用Ansys APDL 命令流实现。

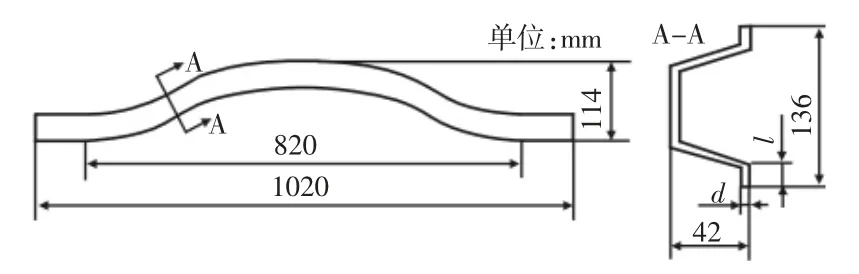
图2 防撞梁几何形状Fig.2 Geometry of Collision Avoidance Beam

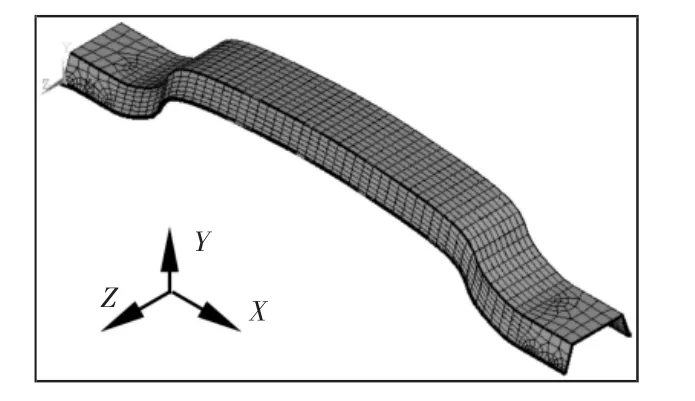
图3 防撞梁有限元模型Fig.3 Finite Element Model of Collision Avoidance Beam

3 材料属性设置

在复合材料层合板设计中，影响层合板性能的因素主要有铺层角和材料属性[6-7]。因此，在微观材料设定方面，考虑层合板材料选择为CFRP，以铺层角度为变量进行优化。设计出满足铺层准则的铺层，且层合板强度性能最优是材料优化的最终目的。

3.1 复合材料铺层设计准则

对于层合板铺层优化要求如下：

（1）层合板采用标准铺层，-45°、0°、45°、90°四种铺层；

（2）为避免层合板中的应力过于集中和层内出现内部微裂纹的情况，通常相同铺层不能连续3 层被选择；

（3）考虑到层合板损伤容限以及后期需对螺栓连接的修补，通常要求各种铺层角度满足一定的层数要求，0°铺层在整个层合板占比中必须在（20～40）%之间，±45°铺层的占比必须在（40～60）%之间，90°铺层的占比必须在（10～30）%之间。

3.2 层合板静态力学性能测试

在试验测试纤维层合板静态力学性能过程中，试验材料选取型号为T300-12K 碳纤维和型号为YPH-209 环氧树脂制备而成的预浸料，采用二步法压力成型制造纤维树脂基复合材料，最后利用机加工的方式将构件切割成矩形试件，如图4 所示。制备成的试验件中纤维体积分数为62%，密度约为（2.0～2.2）g/cm3。静拉伸试验在MTS810 试验机上进行，拉伸速率为0.03kN/s。在拉伸过程中，如图5 所示，通过加入引伸计来测量试件的拉伸应变。根据试验结果，可以得到T300/YPH209 单向层合板静态力学性能参数，如表1 所示。

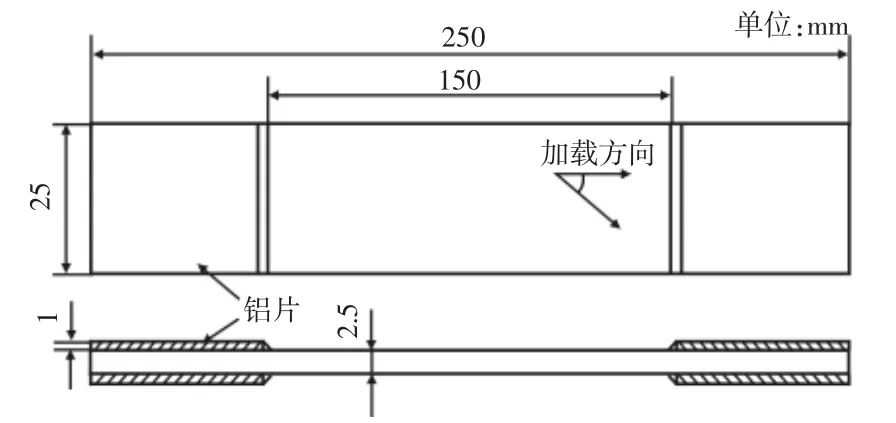
图4 试件的形状和尺寸Fig.4 The Shape and Size of the Specimen

图5 试件与引伸计的装夹Fig.5 The Clamp of the Specimen and Extensometer

表1 材料单向层合板的静态力学性能参数值Tab.1 Mechanical Properties of Materials

4 强度优化设计的遗传算法实现

4.1 强度失效判定准则

针对其他强度理论与实验结果均有不同程度的不一致等问题，文献[8]增加理论方程的项数，提出新的强度准则。对于汽车防撞梁层合板的分析，采用Tsai-Wu 失效准则作为失效判据，在平面应力下的一般形式为：

式中：F1、F11、F12、F2、F22、F66—6 个独立的强度参数，可以由试验测定的基本强度 XT、XC、YT、YC、S 表示出来，计算公式为：

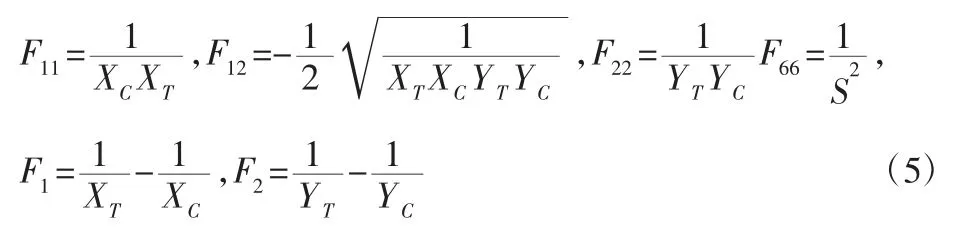
若式（4）左边多项式正好等于1，则材料处于临界状态；若左边多项式大于1，则材料发生破坏；若左边多项式小于1，则材料安全。

4.2 自适应遗传算法

自适应遗传算法（AGA）最早由Srinivas 提出[9]，其基本思想为在遗传过程中动态调整交叉和变异概率，维持种群的多样性，使得算法具有良好的全局收敛能力。目前，自适应遗传算法主要分为两类，一类认为遗传交叉、变异概率大小与迭代次数有关；另一类认为遗传交叉、变异概率大小与平均适应度有关。采用如下的自适应遗传算子：

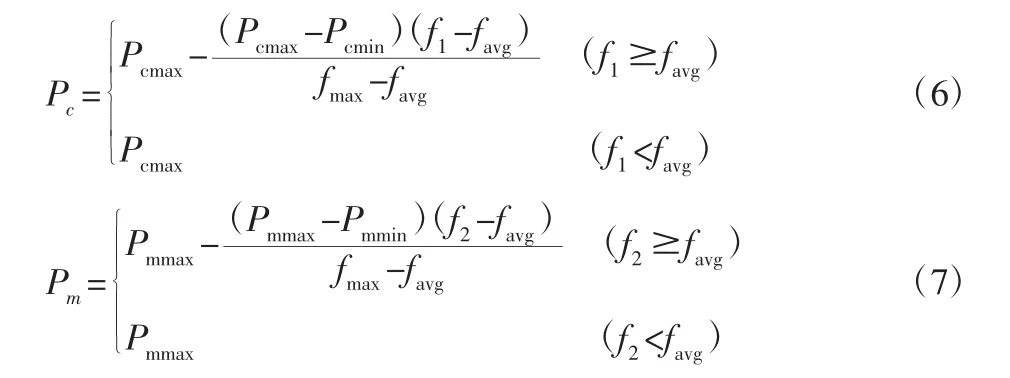
遗传算法中，交叉、变异过程对整个进化代至关重要。将遗传进化过程中个体的状态分为两种，一种是突进状态，在此状态下，遗传目的为丰富种群，个体适应度小于种群平均适应度，给与较大的交叉概率与变异概率，以求接近最优解；另一种为渐进状态，在此状态下，因为个体适应度趋近最优解，为了防止交叉、变异对种群优解的扰动，给与较小的交叉概率与变异概率。

4.3 编码策略

遗传算法中通常采用二进制编码，但对离散变量问题，二进制编码长度与可选离散值有关，所以会出现无法与离散值个数一一对应的问题。采用整数型编码策略，减少了二进制转换为十进制的中间过程，同时也使得设计变量个数与编码长度对应。结构层面将关键控制点横坐标可选区域16 等分，即用［0，1，…，15］表示关键控制点位于的区域编号，同样地，用［0，1，2，3，4］表示截面关键尺寸可选区域编号，用［0，1，2，3，4，5］表示层合板厚度可选区域编号；材料层面用［0，1，2，3］分别表示层合板标准铺层角度［-45°，0°，45°，90°］。

4.4 目标函数

协同优化目标为防撞梁强度最大，引入强度比R 概念，即为在力作用下，层合板极限应力分量与施加应力分量之比：

式中：σi—施加的应力分量对应于σi的极限应力分量。强度比是安全系数的度量，表示至零件失效尚可增加应力的倍数R-1。

在ANSYS 软件中可以对防撞梁模型应力分析，得到其纵向应力、横向应力和剪切应力，以此可以计算出层合板的强度比。强度比小的单层最先破坏，即为最先失效层。由此，适应度值为层合板最小强度比值，适应度函数为：

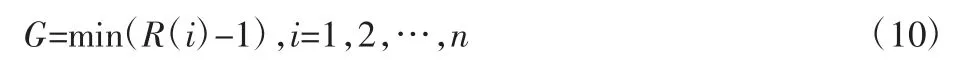
可以建立优化模型如下：

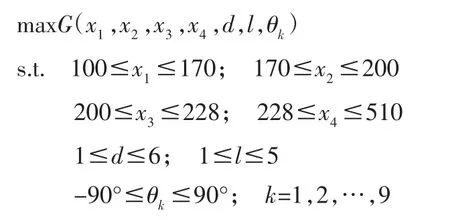
式中：x1，x2，x3，x4—B-Spline 轮廓曲线控制点横坐标参数；l—防撞梁截面关键尺寸参数；d—复合材料层合板铺层总厚度；θk—复合材料层合板各铺层角参数。

5 优化算例

5.1 问题描述

以某汽车的CFRP 防撞梁为优化对象，复合材料采用YPH-209 环氧树脂作为基体，T300 型碳纤维作为增强纤维，纤维体积分数φf=62%。初始化防撞梁轮廓曲线参数为｛x1=105，x2=195.5，x3=204.25，x4=483.75｝，截面关键尺寸为l=4mm；为避免拉伸-弯曲耦合的影响，层合板采用18 层对称铺层，初始铺层为［-45/0/-45/0/0/45/0/0/45］，总厚度初始化为5mm。

5.2 结构/材料一体化设计

汽车防撞梁作为汽车上重要的安全装置，在低速碰撞过程中，车身基本不发生后移，所以在防撞梁与吸能盒螺纹连接处设定为全约束。本次分析过程中，模拟防撞梁在正面受均匀载荷，其数值大小为防撞梁静压试验支反力峰值大小的一半，参考文献[10]中选取均匀载荷大小为175kN/m2，优化模型，如图6 所示。

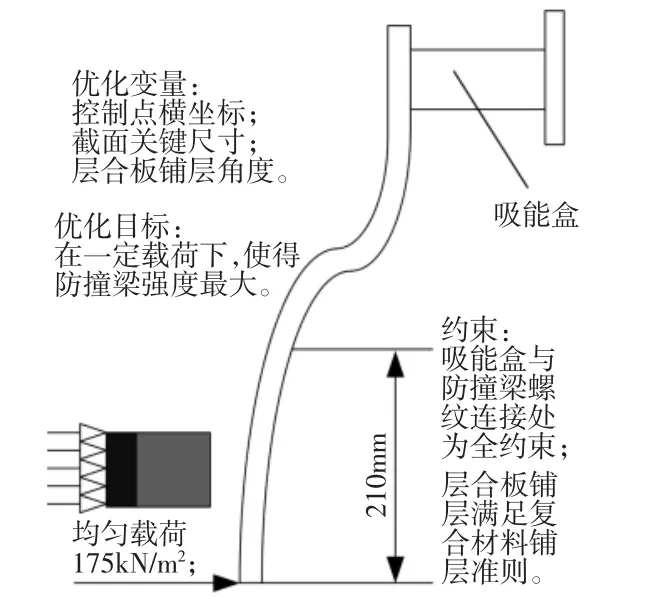
在第一级结构层面设计中，考虑防撞梁截面形状及弯曲程度带来的影响，设计参数为B-Spline 轮廓曲线上关键控制点横坐标xc（c=1，2，3，4），截面关键尺寸l 以及复合材料层合板总厚度d。

在第二级材料层面设计中，考虑层合板铺设角对材料性能造成的影响，设计参数为复合材料层合板各层铺层角度θk（k=1，2，…，9）。

结构/材料一体化优化过程中，运用Matlab 同时对结构与材料两个层面参数构建初始种群，将参数通过后台调用APDL 命令流输入Ansys，完成有限元建模过程。以Tsai-Wu 张量强度比方程创建适应度函数，并采用AGA 算法对种群适应度进行评估，选优淘劣，得到优化方案。由于设计变量较多，使得定义域范围较大且计算结果不易收敛，对设计变量进行离散化，取值范围，如表2所示。

表2 优化设计变量空间Tab.2 Variable Space of Optimal Design

分别采用传统遗传算法（GA）与自适应遗传算法（AGA）对优化模型求解，优化迭代过程，如图7 所示。最大迭代次数为100，GA 算法在64 代结果收敛到最优解，而AGA 算法在37 代结果收敛到最优解，AGA 算法在收敛速度上明显优于GA 算法。最大适应度为3.9744，因此强度比为4.9744，与优化前相比，强度比上升81.41%。汽车防撞梁优化后的结果，如表3 所示。

图7 优化迭代过程Fig.7 Iterative Process of Optimization

表3 结构/材料一体化优化结果Tab.3 Results of Structural/Material Integration Optimization

5.3 有限元验证

采用ANSYS 软件分析初始设计方案的应力结果与一体化优化后方案的应力结果对比，如图8 所示。

由图8（a）可以看出，在防撞梁前端受压条件下，应力集中于防撞梁前端面。由图8（b）可以看出，经过协同优化后的防撞梁应力分布基本与优化前一致，但最大应力从148.702MPa，下降至64.885MPa，降幅为56.4%，说明优化达到预期效果。

5 结论

针对CFRP 汽车防撞梁的强度优化问题，提出一种结构/材料一体化优化设计方法，将B-Spline 轮廓曲线形状、截面关键尺寸及层合板厚度作为结构层面设计参数，将层合板铺层角度作为材料层面设计参数。结果表明：

（1）经过一体化优化后，在满足层合板铺层准则和材料强度的前提下，防撞梁的强度比2.7421 上升至4.9744，升幅为81.41%；防撞梁前端面上的最大Von Mises 应力从148.702MPa，下降至64.885MPa，降幅为56.4%。优化结果达到预期效果，所提出的结构/材料一体化设计方法可以对CFRP 汽车防撞梁进行优化设计，解决传统优化仅考虑单一层面导致优化结果并非整个设计空间最优解的问题。

（2）遗传算法在解决多变量离散问题具有明显优势，提出改进的自适应遗传算法，将整个遗传进化过程分为突进与渐进两个状态。通过算例比较，新算法在迭代收敛上优于传统遗传算法，对解决这类离散问题具有一定的参考意义。