转动热源作用下的制动盘顺序热机耦合分析
2020-08-17潘公宇王继业
潘公宇,王继业
(江苏大学汽车与交通工程学院,江苏 镇江 212013)
1 引言
制动性作为评价汽车性能的主要指标之一,对汽车的行驶安全有很大的影响。据相关资料表明[1]:在道路上由于车辆本身故障所产生的交通事故中,有45%是由制动系统引起的,而制动系统主要问题为“热衰退”和“热疲劳失效”。汽车制动器工作过程中的热机耦合现象会对制动器的性能产生重要影响[2]。因此研究制动器的热机耦合特性能对制动器的工作过程和原理进行深入了解,并为制动器的设计开发提供重要依据。
在使用Abaqus 对盘式制动器进行热机耦合分析时,常用到两种仿真方法:(1)完全热机耦合分析方法;(2)基于固定热源的顺序热机耦合分析方法。考虑到完全热机耦合方法在计算过程中具有高度非线性,求解时不断迭代,所需仿真时间较长,且不容易收敛[3];而第二种方法虽然仿真时间短,但不能模拟转动热源的运动过程[4]。为了弥补以上分析方法的不足,提出了基于转动热源的顺序热机耦合分析方法,首先用紧急制动工况验证了该方法的准确性,然后用于循环制动工况的仿真。
2 模型的建立
2.1 基于转动热源的顺序热机耦合相关理论
由制动器工作原理可知,其摩擦副的接触区域会在制动期间不断地发生变化,形成转动的摩擦热源[5]。当采用传统的基于固定热源的顺序热机耦合方法对制动盘进行仿真时,其热源以完整的圆环形状施加在制动盘盘面上,且固定不动,这与制动的实际情况是不符的,因此提出在制动盘盘面上施加可以转动的热源来模拟实际情况产生的摩擦热源,热源形状与接触区域基本一致。由于采用ABAQUS 软件进行仿真的,在该软件工作界面里无法直接实现热源的转动,需要通过编写子程序来实现[6]。
2.2 顺序耦合分析模型的建立
2.2.1 热分析模型的建立
在进行顺序热机耦合分析时,考虑在ABAQUS 中是以热源的形式施加,而非通过摩擦作用产生,所以只需选取单个制动盘作为研究对象,不考虑摩擦片和制动背板。首先用CATIA 软件建立其制动盘的几何模型,如图1 所示。然后将几何模型以stp 格式导入至Hypermesh 软件中对其进行网格划分、材料属性的赋予、单元类型的设置等,并以inp 格式传递至Abaqus 软件中设置分析步类型,将所受的热流载荷以摩擦副接触区域的形状施加在制动盘表面上。构建完成的分析模型,如图2 所示。

图1 制动盘模型Fig.1 Disk Model

图2 热分析模型Fig.2 Thermal Analysis Model
为实现热源的转动,需在ABAQUS 软件中对结构设置质量流率,通过热传导分析实现热源转动。然而质量流率不支持CAE,不能直接在ABAQUS 操作界面里设置,需要在VisualStudio 中编写用户子程序。对于这里的研究对象,选取制动盘的所有节点作为质量流率的施加区域,并设置为一个集合。在确认材料、分析步、边界条件、载荷等设置正确以后即可输出inp 文件,并在分析步后面手写添加质量流率的关键字。质量流率的具体计算公式需根据不同制动工况在Visual Studio 中编写不同的子程序,最后在提交计算时,调用这些子程序即可。
2.2.2 应力分析模型的建立
接下来进行热应力分析,此时需将分析步类型改为coupled temp-dispalacement 类型,单元类型改为C3D8RT,并将热分析模型所得的温度场模型导入[7]。对于边界条件,由于制动时制动盘所受的机械应力相对于热应力大小可以忽略不计,故不考虑其所受的机械应力,同时,约束制动盘的6 个自由度。
3 模型准确性的验证
基于转动热源的顺序热机耦合分析方法是在基于固定热源的顺序热机耦合分析方法基础上提出的一种能更加准确地模拟实际热源转动情况以及节约计算成本的仿真方法。为了验证其准确性和可行性,在本节使用该方法对制动盘在紧急制动工况下的温升及应力变化情况进行仿真,并将其结果与试验结果进行对比。
3.1 制动过程中的热载荷
在采用顺序热机耦合方法进行分析时采用能量折算法来计算制动过程中产生的摩擦热[8]:

式中:m—汽车质量,1790kg;s—滑移率,0.2;ua—无风条件下汽车的行驶速度;f—滚动阻力系数,0.014;CD—空气阻力系数,0.33;A—迎风面积,1.70m2;ρa—空气密度,1.2258N·s2/m4;i—坡度。其中,制动盘单侧所受的摩擦热量为:

3.2 紧急制动工况下的仿真
设汽车在紧急制动工况下,制动的初始速度为80km/h,制动减速度为5.8m/s2。该工况下不考虑坡度的作用,则制动盘单侧的热流输入值为:

将相关参数代入上式中,可得制动盘热流输入密度与制动时间的变化关系曲线,如图3 所示。其表达式为:
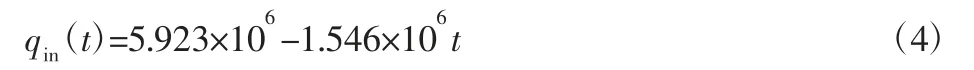

图3 紧急制动工况的输入热流密度Fig.3 Input Heat Flux Density for Emergency Braking Conditions
同时,子程序需给出由制动盘转速变化引起的质量流率的变化以及沿制动盘径向的质量流率的变化,其制动初始时刻的质量流率的表达式为[9]:

式中:qv—制动初始时刻通过单位截面的体积流率;qv在数值上等于 ω0·h,其中,ω0—制动初始转速,66.87rad/s;h—制动盘内某点到轴线的水平距离。
而制动盘内制动任一时刻某点处的质量流率为:

式中:t—制动时间。将相关数据代入,可得质量流率为:

接着只需在ABAQUS 的job 模块中求解时调用该子程序即可,可以发现整个工作过程中,热源在制动盘工作面上是不停转动的,选取四个时刻的热源位置,如图4 所示。

图4 在制动盘上转动的热源Fig.4 Heat Flux Rotated on the Disc Brake
考虑到采用基于转动热源的顺序热机耦合方法对紧急制动工况进行分析时,其工作表面的温度分布与采用完全热机耦合方法进行分析时十分相似,故在此不给出其云图变化特性。同时绘制出制动温度最高所在节点的温升变化曲线,如图5 所示。由图可知采用新方法的温升变化曲线主要呈上升趋势,且出现了“锯齿”状。
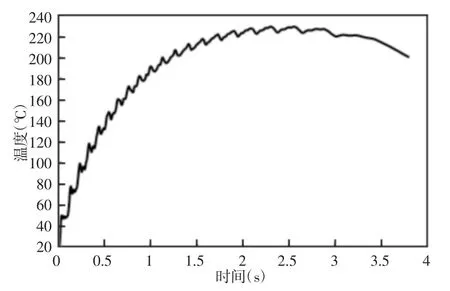
图5 节点温升曲线Fig.5 Temperature Rise Curve of Node
将其与采用完全热机耦合方法、基于固定热源的顺序热机耦合方法时的温升曲线进行对比,如图6 所示。可以发现相对于采用基于固定热源的顺序热机耦合方法更能准确地表现温度的变化情况;但是采用顺序热机耦合的两种方法的最高温度略低于完全热机耦合方法,这是由于采用顺序热机耦合方法时,应力场不对温度场的变化产生影响,而完全热机耦合过程中温度场与应力场是相互作用的,会使温度有所升高。
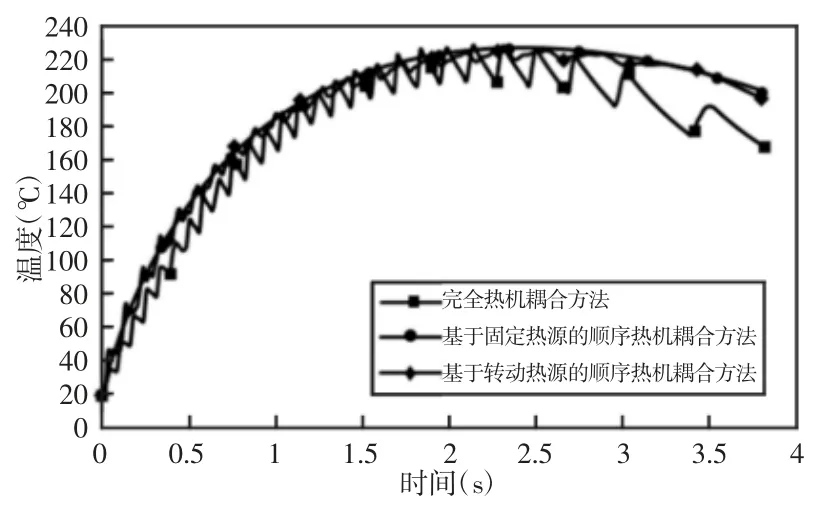
图6 三种仿真方法温升曲线对比Fig.6 Comparison of Three Simulation Methods for Temperature Rise Curve
同样的,紧急制动工况下制动盘热应力分布与采用完全热机耦合方法时基本一致。取制动过程中产生应力最高的一个节点,其应力随时间的变化曲线,如图7 所示。并将其与采用完全热机耦合方法、基于固定热源的顺序热机耦合方法时的应力变化曲线进行对比,如图8 所示。可以发现所得的结论基本与温升曲线一致。

图7 节点应力变化曲线Fig.7 Stress Change Curve of Node

图8 三种仿真方法应力变化曲线对比Fig.8 Comparison of Three Simulation Methods for Stress Change Curve
而由表1 可知,当采用相同配置的电脑进行仿真计算时,基于转动热源的顺序热机耦合方法的最高温度、最大应力与采用完全热机耦合方法所得结果误差很小,却大幅度地降低了计算时间。

表1 三种方法所得仿真结果以及计算时间的对比Tab.1 Comparison of Simulation Results and Calculation Time of Three Simulation Methods
3.3 制动器台架试验验证
为了验证有限元模型的准确性,需进行制动器的台架试验。盘式制动器的温度特性试验采用的试验设备为LINK Dyno 3900型设备,它可以有效模拟制动器在制动过程中温度变化的工况并进行采集。由热机耦合相关研究现状可知,动态测量制动盘表面温度存在许多困难,本实验通过植入热电偶来测试温度。使用台钻在制动盘表面有效摩擦半径处钻孔,并放入热电偶,放入深度为1mm 左右,从而实现在Dyno 3900 型测试台上对制动盘整个制动过程的温度进行实时监测,如图9 所示。装配在试验台架上的制动器,如图10 所示。

图9 制动盘植入热电偶Fig.9 Thermal Sensor Inside of Rotor

图10 装配在试验台上的制动器Fig.10 Disc Brake Assembled on the Bench
试验工况设置为:制动压力为3.635MPa;控制初始温度为20℃。对该工况按照《QC/T564-2008 乘用车制动器性能要求及台架试验方法》对制动盘进行磨合、信号调试和正式试验三个步骤进行试验[10]。
在完成试验以后,经过数据处理可以得到制动盘的温升曲线。将试验结果与有限元仿真结果进行对比,如图11 所示。由图可知,在整个制动过程中,试验与仿真曲线吻合度非常好,最大误差不超过10%,最高温度误差只有1.7%,说明采用的基于转动热源的顺序热机耦合方法是可行的,为后续采用该方法对循环制动工况进行仿真奠定基础。

图11 试验与仿真温度曲线对比Fig.11 Comparison of Test and Simulation Temperature Curves
4 循环制动工况的热机耦合分析
4.1 热边界条件与子程序设置
循环制动工况是驾驶者经常遇到的一种制动工况,由于该制动工况周期较长,如果采用完全热机耦合方法对该工况进行仿真并不容易实现。而前文提出的基于转动热源的顺序热机耦合仿真方法在大幅度降低计算量的同时,还能满足计算精度要求,所以采用上述方法对循环制动工况下制动盘的热相关特性进行仿真分析。GB12676-1999《汽车制动系统结构、性能和试验方法》规定M1类车辆的I 型实验,如表2 所示。

表2 M1 类车辆的I 型试验要求Tab.2 Type M1 Vehicle Type I Test Requirements
试验要求车辆循环制动15 次,在分析时需将整个制动过程分为15 个循环周期,在每个循环周期内车速变化分为三个阶段,第一阶段为制动阶段,第二阶段为加速阶段,最大加速度大小为3.23m/s2,第三阶段为稳速行驶阶段。对应的每个循环周期的输入热流密度的大小也要进行分段处理。由于加速阶段和匀速行驶阶段均没有制动热量产生,因此输入的摩擦热流密度为零,故只需计算制动阶段的输入热流密度大小,其值为:

上式对应的热流密度曲线,如图12 所示。

图12 一个循环制动周期的热流密度Fig.12 The Heat Flux of a Cycle Braking Period
同时,当制动工况为循环制动工况时,在调用用户子程序时还需对质量流率重新进行编写,一个循环制动周期的质量流率表达式如下:

此外,还需对分析步时间进行重新设置,由于一个制动周期为45s,共循环15 次,所以总的分析步时间设置为675s。剩余的步骤与进行紧急制动工况仿真时一致,在ABAQUS 的job 模块中求解时调用重新设置的子程序即可。
4.2 仿真结果分析
4.2.1 温度场分析结果
循环制动工况下温度最高节点的温升曲线,如图13 所示。由图可知,温度是呈波动上升的,且在六到七次循环之后,其波动范围基本保持不变,期间最高温度可达172.9℃。但是在每个制动循坏周期内,盘面节点温度都出现了较大的波动,在制动阶段,温度迅速上升,而在接下来的加速阶段,制动盘只受到对流换热作用,并无热流输入,所以盘面温度会逐渐下降。在整个制动过程中,由于每个制动循环周期都较长,制动盘有足够长的时间散热,因此整个制动过程中并未产生特别高的温度。

图13 循环制动工况下的盘面温度曲线Fig.13 Temperature Change Curve of Disk Surface in Repeated Braking
选取与温度场分析时同样的节点,循环制动工况下该节点的应力变化曲线,如图14 所示。由图可知,热应力随时间的变化曲线与温升变化曲线基本一致,都是呈波动上升且逐渐趋于动态平衡。在一个制动周期内,制动盘盘面的最大热应力为85.7MPa。

图14 循环制动工况下的盘面热应力变化曲线Fig.14 Thermal Stress Change Curve of Disk Surface in Repeated Braking
5 结论
针对采用完全热机耦合方法对通风盘式制动器进行热机耦合分析时存在非线性程度高、计算量大、不容易收敛等问题,而传统的基于固定热源的顺序热机耦合方法无法准确地模拟热源的实际转动情况,因此提出一种基于转动热源的顺序热机耦合方法。该方法主要通过对制动盘结构设置质量流率,并在用户子程序编写质量流率的相关代码,同时在计算时调用该子程序来实现热源的转动。当采用该方法对紧急制动工况进行仿真分析时,可以发现该方法不仅计算成本低、容易实现收敛,而且仿真结果与采用完全热机耦合方法所结果、试验结果曲线基本吻合,从而证明了该方法的可靠性。最后将其应用对循环制动工况的仿真中,可以发现在循环制动工况下,制动盘盘面温度呈周期性的波动上升,并趋于稳定,同时热应力的变化趋势与温度也基本一致。
