水轮发电机组轴系刚度近似计算方法

杨光波，曾云，张记坤，王芳芳，张振凯，钱晶

(昆明理工大学冶金与能源工程学院，云南 昆明 650093)

水轮发电机组作为大型的旋转机械，在运行中存在着振动和摆动的问题，严重影响了机组的运行安全，甚至导致了机组结构的破坏，造成事故.随着越来越多的大型水力发电机组投入运行，因其大尺寸、相对刚度弱等引起的轴系振动问题，已经成为影响大型水力发电机组稳定运行的关键技术问题.因此提高轴系支撑系统的刚度，对于保障机组稳定运行具有十分重要的意义[1].在研究水力机组轴系振动方面，前人已经取得了许多的研究成果.例如：通过将复杂的轴系结构简化为离散的集中参数模型，得到轴系振动的基本特性[2-3]，理论推导或利用仿真软件建立水力机组轴系模型[4-5].李耀辉等[6]提出了水泵机组轴系支撑刚度的计算理论和方法.除理论研究之外，水力机组现场试验方面也取得一些有效成果[7-8].傅丽萍等[9]分析了机组上机架振动超标的原因，给出了一种估算上机架径向刚度的方法.这些针对具体的水力机组开展的研究，对于解决机组在运行中的振动问题以及探索水力机组振动的共性问题，具有积极的参考价值.但是，目前针对实际运行的水电机组的轴系支撑刚度理论计算和现场测试方法的相关研究较少，因此，开展对水轮发电机组轴系支撑刚度的理论计算和研究就显得十分必要.

在机组的实际运行中，引起振动的原因有电气、机械及水力脉动3个方面.电气方面主要是由于定、转子间气隙不均匀引起的不平衡磁拉力[10]；机械方面主要是机组转动质量不平衡、导轴承不同心以及轴线不正引起的[11]；水力方面主要是由于转轮不圆、导叶、叶片开口不均、线性不好等原因产生水力激励，而导致水力机组主轴系统激烈振动[12].然而，对于实际运行中的机组，目前尚无有效的方法实测机组轴系支撑刚度数据.

文中基于立式水力发电机组集中参数模型，建立水力发电机组转子和转轮的简化运动微分方程.根据发电机组特殊运行工况，简化附加外力，结合仿真运行模拟系统得到的振动幅值，提出一种近似计算轴系刚度的计算方法.本研究在理论上进行积极的探索，拟为实际工程提供一定的参考.

1 轴系基本模型

将立式水轮发电机组轴系简化为如图1所示的二圆盘三支撑结构模型，图中B1，B2，B3分别为上导轴承、下导轴承、水导轴承的几何形心；O1，O2分别为发电机转子和水轮机转轮的几何形心；r1，r2分别为发电机转子和水轮机转轮的径向位移；r3，r4，r5分别为机组大轴在上导、下导、水导轴承处的位移.

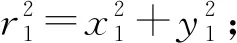
参考文献[13]的推导，根据经典拉格朗日方程，推导出水力发电机组在稳态运行状态下发电机转子和水轮机转轮的振动微分方程为

(1)

(2)

(3)

(4)

式中：m1，m2分别为发电机转子和水轮机转轮的质量，kg；c1，c2分别为作用在发电机转子和水轮机转轮处的阻尼系数，N/m；Fx1，Fy1为作用于发电机转子上的附加外力X，Y方向的2个分量，N；Fx2，Fy2为作用于水轮机转轮上的附加外力X，Y方向的2个分量，N；φ为机组旋转角度；K11，K22，K12为组合刚度，N/m.其中组合刚度的计算公式分别为

(5)

式中：K1，K2，K3分别为上导、下导和水导轴承支撑刚度，N/m.

讨论1：上述模型中，发电机转子上的附加外力包括不平衡磁拉力，水轮机转轮上的附加外力包括密封力、转轮叶片不均衡力、水力激励力等.文中将这些附加外力保留不变作为附加的输入激励，目的在于使得所建立的模型具有通用性，能应用于对各种外力的分析.如需考虑某种作用力对轴系的影响时，只需将具体的作用力代入模型即可.

(6)

式中：r1为发电机转子摆度圆半径；r2为水轮机转轮摆度圆半径.X1，X2分别为发电机转子和水轮机转轮X方向的摆度值.

水力发电机组在稳态工况下运行，机组转速不变，即ω恒定，m1e1ω2为常数.假设稳态工况下近似为常数，则轴系振动微分方程(1)—(4)实现了刚度解耦，变为单自由度强迫振动微分方程的形式.根据经典振动理论，可直接写出X方向的振动解析表达式为

(7)

(8)

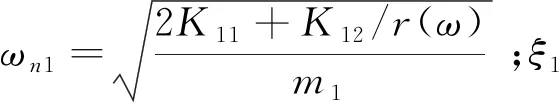
由于转子与转轮Y方向振幅与X方向相同，只相差90°相位，因此只列出X方向振动解析表达式.

2 轴系刚度的简化计算

2.1 振动表达式的简化

文中目的是尝试利用振动测试数据计算轴系支撑刚度.在水轮发电机组轴系振动测试中，通常只能测试主轴关键点的摆度数据.轴系振动解析表达式(7)—(8)中包含许多变量，比如固有频率角速度、阻尼比和附加外力，这些变量在机组实际运行中很难直接测量，因此根据轴系振动的稳态特征，对上述方程进行简化

假设1：根据轴系特性分析可知，在机组稳态运行条件下，作用于水力机组转子和转轮处的阻尼系数c1和c2对轴系稳态振动幅值影响很小，因此可近似地认为c1=0，c2=0，近似取阻尼比ξ1=0，ξ2=0.

根据假设1，机组形心轨迹方程(7)—(8)可简化为

(9)

(10)

式中：φ10为转子初始相角；φ20为转轮初始相角.

由旋转机械动力学可知，作用于旋转机械中的附加外力可采用角速度的周期函数来表示.由于文中忽略阻尼系数对机组轴系稳态振动的影响，记作用在发电机转子上的附加外力为Fx1=F10cos(ωt)，Fy1=F10sin(ωt)；作用在水轮机转轮上的附加外力为Fx2=F20cos(ωt)，Fy2=F20sin(ωt)，其中F10，F20为周期性附加外力的幅值.文中只考虑周期性外力的基频分量.

简化后的振动解析表达式(9)—(10)中只剩1项附加外力项.由于作用于转子和转轮上的附加外力尚无系统、有效的方法进行测试，文中考虑在一些特殊运行工况下，对附加外力进行简化处理.

针对机组运行的特殊工况，考虑到作用于转子与转轮上的附加外力F这一变量，将轴系刚度分转子侧与转轮侧2个部分计算.

2.2 等效刚度K11，K12计算

假设2：空转工况下，发电机转子的振动仅受自身质量偏心引起的机械不平衡力作用，近似认为转子没有附加外力作用，即F10=0.

假设3：空载工况下，发电机转子除受自身质量偏心引起的机械不平衡力和不平衡磁拉力作用，不平衡磁拉力即转子附加外力F10.

发电机转子摆度幅值近似为转子形心轨迹幅值的2倍.根据上述假设2、假设3，联立空转工况和空载工况，利用转子振动式(9)推导得到空转工况与空载工况下发电机转子X方向的振动幅值为

(11)

(12)

根据空转工况与空载工况下的摆度数据(实测或仿真)，联立式(11)—(12)，即可推导得到

(13)

(14)

2.3 等效刚度K12,K22计算

假设4：在调相工况，水轮机转轮区域没有水流作用于转轮，转轮上的附加外力近似为0，即F20=0.

假设5：在额定工况下，机组处于稳定运行状态，转轮区域水力不平衡，附加外力较小，但不为0，记转轮上的附加外力为F20.

水轮机转轮摆度幅值近似为转轮形心轨迹幅值的2倍.根据上述假设2、假设3，联立调相工况与额定工况，利用转轮振动表达式(10)推导得到调相工况与额定工况下水轮机转轮X方向的振动幅值为

(15)

(16)

于是，利用调相工况和额定工况下的摆度数据(实测或仿真)，联立式(15)—(16)，推导得到

(17)

(18)

讨论2：由于机组偏心不变，假定在调相工况、空载工况、额定工况下发电机转子处的不平衡磁拉力恒定不变.

讨论3：上述公式中的附加外力F10，F20是作用在转子和转轮上的各个作用力的合力，因此，根据线性迭加原理，振幅等于各个力分别作用所产生的振幅之和.

讨论4：在单一工况下求解组合刚度，虽然可以根据运行工况的特殊性，转子与转轮处附加外力项为0，使得刚度项是关于形心轨迹的函数，但由于没有附加外力的情况下，仿真得到转子或转轮X与Y方向的振动幅值相同，不能求解出组合刚度值.因此，采用工况组合的形式，结合2种工况下转轮或转子X方向(Y方向)的振幅求解组合刚度，避免了X与Y方向的振幅相同的情况.

3 仿真模拟计算

对于实际运行的机组，目前尚无有效的方法实测机组轴系上各种不平衡力，也不能够实测机组轴系支撑刚度数据，开展试验研究有困难.因此，采用已建立的水力机组运行模拟系统进行仿真，其中模拟系统中给定轴系刚度等特征参数，将其作为理想系统.

在理想系统中给定不同的附加外力值，仿真得到机组摆度幅值，并假设其仿真结果与实际机组振动是一致的.利用仿真计算得到轴系摆度数据，采用文中所提出的近似计算公式计算刚度数据.

3.1 水轮发电机组轴系仿真系统

为较好地模拟实际机组在控制器控制下的行为特征，选择如图2所示的仿真系统.调速器采用经典的并联PID结构，控制参数：KP=5.0，KD=1.3，KI=1.7，bP=0.04；励磁控制系统采用恒功率因数方式的PI控制，KP1=1.0，KI1=1.5；对象系统采用弹性水击水轮机模型和三阶发电机模型，机组暂态过程中的3个参数Mt，Mg，ω作为轴系模型的输入.

3.2 轴系刚度计算

某电站的机组参数和轴系几何参数如下：发电机转子质量m1=46 600 kg，水轮机转轮的质量m2=24 000 kg，发电机转子半径R1=4.646 m，水轮机转轮半径R2=1.708 m，角速度ω=13 rad/s.

轴系特征参数：上导轴承、下导轴承和水导轴承的刚度分别为K1=2.0×108N/m，K2=2.0×108N/m，K3=3.5×108N/m，a=3.0 m，b=3.5 m，c=1.2 m.

图3，4为在调相工况与额定工况下模拟得到水轮机转轮形心轨迹图和水轮机转轮X方向振幅图，图中Y2为转轮Y方向振幅，X2为转轮X方向振幅，t为时间.

调相工况下，在运行模拟程序中给定e1=1.0mm，e2=0.5mm，发电机转子磁拉力的幅值为MgB·ad，ad=0.006，频率为2 Hz，水轮机转轮附加外力为0，并进行仿真，由此得到水轮机转轮形心轨迹图和X方向的摆度图.

额定工况下，在运行模拟程序中给定发电机转子磁拉力的幅值为MgB·ad，ad=0.006 0，频率为2 Hz，水轮机转轮附加外力幅值为MgB·ad，ad=0.005 0，频率根据经验公式计算为0.17 Hz，并进行仿真，由此得到水轮机转轮形心轨迹图和转轮X方向的摆度图.

首先根据仿真图形，图3，4中水轮机形心轨迹分别为类似于同心圆状和花篮状，转轮X方向振幅则呈周期性的变化，表明机组运动状态不稳定.文中主要考虑机组稳态下的振动形态，对上述情况不做主要研究.

多次仿真表明，产生上述结果的主要原因：① 附加外力幅值给定偏大；② 根据经验公式计算得到的附加外力频率误差较大；③ 在理想状态下转子与转轮的振幅是由其自身质量偏心所决定的.

同时，从侧面也反映出文中所采用的运行模拟系统是一种有效的模拟方法，能够真实地模拟出机组在不同工况下的运行状态.

经过多次仿真试算，最终确定水轮机侧各参数分别为不平衡磁拉力的幅值MgB·ad，ad=0.0009，额定工况下转轮上的附加外力幅值MgB·ad，ad=0.0009，附加外力频率均为机组转频f=2.0833 Hz，发电机转子与水轮机转轮偏心e1=0.1 mm，e2=0.2 mm.

按上述参数仿真得到额定工况下发电机转子X方向和水轮机转轮X方向的振幅图,如图5所示，图中X1为转子X方向振幅.

取得发电机转子X方向和水轮机转轮X方向振幅最大值为X′10=1.2771×10-2mm，X′20=1.5245×10-2mm.同样仿真得到调相工况下发电机转子X方向和水轮机转轮X方向振幅最大值为X10=1.3734×10-1mm，X20=5.5362×10-2mm.

联立上述2种工况计算得到K12=3.2821×107N/m，K22=1.284 1×108N/m.

相较于图3—5所示的振动形式为等幅振动，表明机组受力较为稳定，是稳态下的振动形态，且刚度计算值也更接近比较值，表明上述试算确定的参数较为合理.

采用相同的方法，对发电机侧附加外力的合理性进行仿真试算，最终确定各参数分别为不平衡磁拉力的幅值MgB·ad，ad=0.0009，空转(空载)工况下转轮上的附加外力幅值MgB·ad，ad=0.0051，附加外力频率均为机组转频f=2.0833 Hz.按照上述确定参数，仿真空转工况与空载工况.根据仿真数据，计算得到K12=1.6790×107N/m，K11=1.9891×108N/m.

对上述2种系统下计算结果给出说明：

1) 以上2种系统均是在假设条件下计算求得的组合刚度，有一定的局限性，同时存在对轴系考虑不周全情况.

2) 该耦合刚度项是在3个导轴承的支撑刚度折算到水轮机转轮和发电机转子的运动描述中产生的中间量，反映了水轮机转轮和发电机转子之间通过主轴的相互耦合作用.根据轴系的机构尺寸，假想在2种系统下计算得到的耦合刚度对于主轴影响的权重不同，可能存在一种算法关系，即K12=a1·K′12+a2·K″12.对于上述假想的合理性，在后续研究中再继续深入讨论.

3) 通过试算，当a1=0.95，a2=0.05，其组合刚度值K12=3.202 0×107N/m时，计算得到的刚度值K1,K2,K3最为接近给定值.

将计算得到的组合刚度K11,K12,K22分别代入式(5)，求解线性方程组，计算结果列于表1.

表1 刚度计算结果

误差分析：

1) 从表1中可以看出，除K2相对误差值较大之外，其余刚度值的相对误差值均在10%以内，甚至更低.对于K2相对误差值较大这一结果，初步假设可能是由于K11计算值相对参考值较小引起的.

2) 所提出的近似计算方法忽略了阻尼系数带来的影响，在振动解析表达式的基础上进行了简化，因此其计算结果存在一定的误差.对于简化的阻尼系数与阻尼比对于轴系刚度计算的影响，在后续的研究中将进一步讨论.

4 结 论

水力发电机组轴系支撑刚度是轴系振动的核心参数，是应用经典动力学研究水力发电机组轴系振动的基本前提.文中提出的轴系刚度计算方法，是根据水力机组在特殊工况的特殊性，给出了一些假设和近似处理，但这些近似和假设的合理性仍需进一步验证.

在实例计算中，发电机转子和水轮机转轮的振动幅值是在不同出力下给定不同附加外力幅值，并仿真运行模拟系统而获得的.附加外力值给定不同，其转子与转轮振动幅值也不同，因此刚度计算的绝对准确性有待进一步验证.但是，文中提出的方法对于轴系支撑刚度的计算是一种创新，为在运行的大型水力发电机组轴系支撑刚度的计算提供了一种新方法.