基于ESI数据的数学学科竞争力对比分析研究

刘兵红

摘 要：[目的/意义]当前我国高校正在进行“双一流”建设，为高校学科发展带来了新的机遇。本文通过对比进入ESI前1%的北京大学、兰州大学、上海交通大学、清华大学、武汉大学这5所高校数学学科的竞争力，找出各校的比较优势与差距，为高校数学学科的特色发展、融合发展、合作发展提供指导。[方法/过程]采用文献计量学的分析方法，通过发文量、发文期刊、引文数、高被引论文、学科领域分布、基金分布、合作机构、研究热点等进行对比分析，了解不同高校数学学科发展过程中的科研表现。[结果/结论]5所高校的发文数量有稳步上升趋势;高质量的论文对学科发展起着引领作用;数学学科的研究越来越体现了学科间的交叉、融合;国家自然科学基金是助力学科建设的主要力量;与高水平机构联合是提高学科影响力的有效途径;近十年来的研究热点主要集中在方程、计算、统计、最优化等方面;各校的核心館藏的保障率还有待提高;兰州大学、武汉大学的师资队伍建设方面还需要加强。

关键词：ESI;数学学科;竞争力;对比分析

DOI：10.3969/j.issn.1008-0821.2020.02.016

〔中图分类号〕G250.252 〔文献标识码〕A 〔文章编号〕1008-0821（2020）02-0141-12

Comparative Analysis Research on Mathematical

Subject Competitiveness Based on ESI Data

——Take the Five Universities of Entering ESI Top 1% as an Example

Liu Binghong

（School of Mathematics and Statistics，Wuhan University，Wuhan 430072，China）

Abstract：[Purpose/Signficance]At present，universities in China are carrying out“double first-class”construction，which brings new opportunities for the development of disciplines in Chinas universities.In this paper，five universities including Peking University，Lanzhou University，Shanghai Jiaotong University，Tsinghua University and Wuhan University which ranked the first 1% of ESI were selected to conduct comparative analysis，and found out the comparative advantages and shortcomings.It provided guidance for characteristic development，integrated development and cooperative development of subjects in universities.[Method/Process]By means of bibliometrics，through the comparative analysis of the number of papers，high-cited authors，cooperative institutions，subject branches，research hotspots，etc.，We found the scientific research performances in the development of mathematics disciplines in different universities.[Result/Conclusion]The number of papers in five universities was steadily increasing;The highly quality papers played leading roles in the development of the subjects;The research of mathematics discipline more and more reflected the intersection and integration of disciplines;The National Natural Science Foundation of China was the main force to help the discipline construction;Cooperation with High level institutions was an effective way to improve the influence of disciplines;The research hotspots in the past ten years mainly focused on equation，calculation，statistics，optimization，etc.;The guarantee rate of the core collection of mathematics still needs to be improved;The construction of teaching staff in Lanzhou University and Wuhan University needs to be strengthened.

Key words：ESI;mathematics subject;competitiveness;comparative analysis

2015年11月，国务院正式印发《国家统筹推进世界一流大学和一流学科建设总体方案》，进一步明确了推进“双一流”建设的总体目标、具体任务和支持措施[1]。2017年，国务院发布的《国家教育事业发展“十三五”规划》中进一步丰富了“双一流”建设的内涵和方式。“双一流”建设是对我国现有高等教育发展重点支持政策的改革与完善，已经并将持续引发包括现有国家重点大学、非重点大学、地方大学等在内的高等学校的高度关注和新一轮竞争[2]。

在此背景下，各高校越来越关注和重视自身学科在国际上的地位，而基础学科的建设是高校发展其他应用学科的学科储备和前提条件，强大的数学、物理、化学、生物等基础学科是一流大學的共同特征。如武汉大学根据“中国特色、世界一流”的要求，提出“一流基础学科行动计划”[3]，以世界一流标准重点建设基础学科，支撑一流大学的整体建设等。

鉴于数学学科作为基础学科在推进“双一流”学科建设中处于重要的地位，为了加快“双一流”的建设目标，促进数学及相关学科发展，提升学科的核心竞争力，我们将学科服务融入学校学科建设的总目标，选取了目前国内进入ESI前1%的5所高校北京大学、兰州大学、上海交通大学、清华大学、武汉大学的数学学科进行对比分析，从不同维度揭示5校的科研竞争力，找出高校学科发展的优势和不足，便于高校学科建设的决策者找出问题和差距，提出针对性地、合理的学科发展对策，从而提高其国际竞争力和影响力。

1 相关研究文献

目前国内外有一些学者对学科竞争力进行了研究，如李健宁[4]认为学科竞争力是指各高校同一学科之间在某些方面的比较优势或差距表现，提出利用因素分析法、内涵解析法和标杆测定法建立实证分析模型，以此来评价中美两国的学科竞争力;唐琳等[5]利用SciVal分析平台对我国9校联盟与3所世界一流大学的科研产出、学科布局和竞争优势进行了对比分析;邱均平等[6]基于ESI数据，对1995-2005年的“985”高校进行了科研竞争力指标的分析;陈淑云等[7]基于高水平论文的中美“常春藤”高校学科对比分析;Ge Y[8]以江汉大学材料学科为例，利用ESI和Incites数据库，对没有进入ESI前1%的学科竞争力进行分析;Anthipi P等[9]通过ESI数据库，对南非大学各学科领域竞争力进行的比较，为调整高等教育的政策提供依据。

当前大部分文献的研究主要针对多个高校的整体学科领域进行对比分析，同一学科各个高校之间，特别是基于ESI数据，对国内顶尖高校的横向对比分析的文献数量较少。由于高校间无法获取对同一学科竞争力的发展评价，不利于高校学科的特色发展与科研合作。本研究基于ESI数据，利用文献计量工具，对进入ESI前1%的5所国内顶尖高校的数学学科，从论文数量、发文期刊的分区、高被引论文、基金分布、合作机构、学科领域分布等进行学科竞争力的对比分析，揭示数学学科领域国内一流高校的研究现状。

2 数据来源与研究方法

2.1 数据来源

ESI（基本科学指标）是科睿唯安集团在汇集和分析ISI Web of Science（SCIE/SSCI）所收录的学术文献及其所引用的参考文献的基础上建立起来的分析型数据库。ESI是以近11年的论文为引用数据，每2个月进行一次数据更替，ESI学科的排名会随着数据更替产生动态变化。2018年11月发布的ESI数学学科有252家机构进入前1%，此次研究的5所高校全部进入，具体排名见表1。

2.2 研究方法

本文将Web of Science数据库作为文献统计来源，根据ESI收录评价论文的标准，对这5所高校2008-2017年SCIE整年的论文数据进行下载，利用Excel的Vlookup函数查找功能和ESI数学学科期刊源进行比对，找出这5所高校的ESI数学学科的论文，筛选出有效论文6 452篇。笔者基于这5所高校的数据，利用Pandas等工具来清洗并处理数据，进行多角度分析。

3 研究现状对比分析

3.1 发文量

衡量某领域发展的重要指标就是学术论文数量的变化，对其文献分布作历史地、全面地统计，绘制相应的分布曲线，为评价该领域所处的阶段，预测发展趋势和动态具有重要意义[11]。因此，我们将检索到的5所高校的ESI数学学科，按照年度进行统计，并绘制成曲线图，如图1所示。

图1 5校数学学科发文量年度分布（2008-2017年）

从图1可以看出，北京大学从2008-2017年，每年的数学学科的论文发文量都是排名第一。上海交通大学和清华大学一直保持平稳的发展状态;武汉大学处于稳步攀升的态势，到2017年排名第二;兰州大学的发文量相对较少。

3.2 发文期刊

通过分析5校发表ESI论文期刊的JCR分区，可以进一步了解各校的发文质量，具体见表2。

从表2可以看出，兰州大学发文期刊1区占比最大，达到50%，说明该校在数学领域顶级期刊上的发文较多，论文的质量较高;其次是上海交通大学、北京大学、清华大学;武汉大学2区的发文量占比最大，达到30%，表明该校学科有巨大的发展潜力。

3.3 引文数

引文数是从使用者的角度评价科学家、期刊、机构、国家科学水平的一个基本指标，是论文被引用的全部次数，它用客观使用的数量反映了科学体在科学发展和文献交流中的作用。其值越大，表明该科学家、期刊、机构、国家作用越重要[12]。表3列出5校中被引次数排前10的论文作者。

从表3可以看出，高被引作者对数学学科研究的高影响力，其科研成果引领着学科研究的方向。学校拥有更多的高影响力作者，对ESI国际排名有着非常重要的作用。如兰州大学有多位引文数超高的科研工作者，该校的国际排名81。其中排名第一的Li Wantong，文章被引次数高达1 755次，是其他高校高被引作者的数倍。

3.4 ESI高被引论文

ESI高被引论文指近十年来被引频次排在前1%的论文，高被引论文的内容一般属于该学科的重点研究领域，是诸多研究成果的提炼[13]。通过WOS数据库对ESI高被引文献的标注功能，找出5校的2008-2017年高被引论文，分别是北京大学24篇，兰州大学18篇，上海交通大学23篇，清华大学14篇，武汉大学13篇。通过作者单位的分析发现，高被引论文来自于学校多个院系的贡献，具体见表4所示：

从高被引论文数可以看到，北京大学的ESI高被引论文最多，其次是上海交通大学、兰州大学;从表4的高被引论文贡献单位分布可以看出，数学学科领域的研究，除了来自数学学院，其它院系的贡献也非常大，如北京大学占33%，上海交通大学占43%，武汉大学占31%。高被引论文的院系分布在一定程度上也体现了学科的交叉融合。

3.5 学科领域分布

ESI的学科评价方法是将每一种期刊都归类为22个学科中的一类来进行分析，但有些期刊中的文献涉及了多个学科。固化的期刊分类，无法真正体现文献的跨学科性。这种期刊中文献内容与期刊学科分类不一致的情况，忽视了多学科交叉研究的重要性，不容易发现和挖掘出学科在微观领域的竞争优势，也不能细致地体现一些在交叉学科中贡献度占比并不高的学科参与度情况[14]。因此，我们利用SCIE数据库，对5所高校发文的学科领域分布进行分析，具体见表5。

从表5的研究领域分布的论文数可以看出，北京大学在各研究领域都占有绝对优势，清华大学在应用数学、武汉大学在统计学与概率论，上海交通大学在数学跨学科应用方面也很强;除此之外，5所高校发表论文涉及的研究领域比较广泛，最多达到22个，体现出学术研究具有很强的跨学科性，其中数学学科与物理、计算机、生物、自动化与控制的交叉性最强。

3.6 承担基金项目

研究各类基金项目资助发表论文的情况，不仅可以了解该领域相关研究的重视程度及当前的研究前沿或热点，还可以反映该领域研究论文的质量水平[15]。我们选取了资助各校发文排前5的基金进行了比较分析，具体见表6：

从表6可以看出各类基金在促进学科整体科研实力、提高学术水平等方面的重要作用。其中，国家自然科学基金无论从发文量还是总被引频次来讲都是最多的，对学科建设的支持力度最大，效果也是最好。因此，是否获得国家自然科学基金的资助，不仅是学术界从事基础研究最重要的一个指标，也是衡量同行对科研工作认可度的一个最客观的指标。

3.7 合作机构

目前，我国“双一流”遴选条件中亦要求高校深度参与国际或区域性重大科学计划、科学工程，与世界高水平大学和学术机构有深度的学术交流与科研合作[16]。克罗地亚学者NevenkaPravdi等通过研究科研合作与科研产出之间的关系，论证了合作有助于提高科研产出，且同一批论文作者间的合作频率越高，科研产出越高[17]。我们通过对5校的ESI数学学科论文的国内和国际上的合作机构分析，从深度和广度上进一步了解，同时可以寻找潜在的、优质的跨机构研究项目的合作伙伴。具体的国际合作论文数以及合作国家/机构分布见图2和表7。

从图2可以看到，国际合作数量北京大学859篇，占比49%，兰州大学237篇，占比24%，清华大学593篇，占比44%，上海交通大学700篇，占比55%，武汉大学442篇，占比41%。

从表7数据可以看出，5所高校的数学学科国内与国际合作与交流日趋频繁，合作规模也越来越大。国内合作机构以本地的研究机构为主，国际合作的国家或机构大多与该校的发展历史有一定关系，如武汉大学的国际合作单位以法国高校为主，与武汉大学的中法数学交流始于1980年的中法数学班。

从数据中也不难发现，与国内著名研究机构如中科院或者与美国的一流研究机构合作的学校，合作次数越多，总被引次数也越高。如北京大学排前3国内合作单位基本都是985高校或著名的科研机构，国际上合作的全部是美国名校，合作的论文数量和被引次数都比其它学校多。

3.8 研究热点

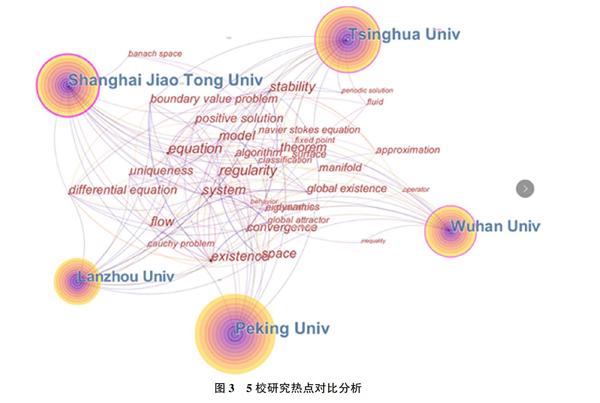
研究热点可认为是具有相当数量且存在一定内在联系的一组论文共同探讨的问题，而关键词是一篇论文主要内容和核心观点的精炼，高频关键词集合可代表一个学科领域内的研究热点[18]。笔者利用Citespace软件，生成了机构（Institution）—关键词（keyword）的共现网络，以此探析2008-2017年5所高校数学学科的研究热点。为了更清晰的显示结果，只选取了排前20的关键词，如图3所示。

从图3可以看到，5所高校与Equation，Boundary Value Problem，Algorithm，Manifold，Approximation，Theorem等關键词存在密切的关系，通过对关键词以及相关关键词下的高被引文献分析，北京大学的研究热点主要集中在微分几何[19]、统计[20-23]方面;兰州大学研究热点主要集中在计算[24-27]和偏微分方程[28]方面;清华大学研究热点主要集中在偏微分方程[29-31]、常微分方程[32]等方面;上海交通大学研究热点主要集中在计算[33-36]、统计[37]等方面;武汉大学研究热点主要集中在概率[38-39]、应用数学[40]、偏微分方程[41]等方面。

4 核心馆藏保障

对于数学学科的建设，文献资源的保障是工作的核心任务之一。为了解5校的重点文献资源保障情况，我们对这5所高校收藏的488种ESI数学来源期刊进行了一个全面地调查，具体各校馆藏资源保障情况见表8。

5校的馆藏数据显示，清华大学的文献保障率最高，达到80%，其次是武汉大学、上海交通大学、北京大学，最后是兰州大学。通过馆藏目录的检索，发现这5所高校电子资源的保障率较高，大都购买了Springer、SIAM、Jstor、Oxford、Taylor & Francis等主要的数学专业的数据库。

5 师资力量

师资队伍是学科的核心竞争力，首先是专业技术水平的职称，高校具有高级职称教师的比例很大程度上代表了高校的高水平师资条件;其次是国家层面有科学技术领域最高荣誉称号的中国科学院院士和中国工程院院士，以及教育部层面的长江学者奖励计划、国家杰出青年基金、高等学校优秀青年教师计划等，都是国家造就杰出的学科带头人的重要举措[42]。通过网上的调查，5校的数学学科的师资力量主要体现在以下几个方面，具体情况见表9。

从表9可以看出，北京大学在学科人才方面，有着其它高校无法比拟的优势，拥有7名院士，11名长江特聘教授、24名杰青、10名优青。清华大学有高级职称的占教师人数的98%，学科研究的实力也是非常雄厚。如果对高级职称的教师进行细分，可以看出北京大学的教授与副教授的比例是2.68∶1，上海交通、清华大学的教授和副教授的比例大约持平，而武汉大学教授与副教授的比例是1∶1.59。

6 结论与建议

通过对比分析结论如下：从发文量来看，5所高校的发文数量处于上升趋势，表明数学学科的发展具备良好的发展态势;从引用次数和高被引论文来看，各校都有比较突出的学科带头人;从高被引作者单位和学科领域分布来看，数学学科的研究越来越体现了学科间的交叉、融合;从基金项目的分布来看，国家自然科学基金是助力学科建设的重要力量;从合作机构分布来看，与高水平机构联合是提高学科影响力的有效途径;从研究热点来看，主要集中在方程、计算、统计、最优化等方面，同时各有研究侧重点;从ESI发文期刊的收藏情况来看，核心馆藏的保障率还有待提高;从师资队伍的建设方面来看，兰州大学以及武汉大学还需要加强。基于上述结论，为推进我国高校一流基础学科建设和发展提出以下建议：

6.1 完善评价指标

科学社会学家默顿（Merton R K）曾经指出了学界的累积效应，即一位学者发表的论文越多，他被其他学者了解的概率越大，这样他被其他学者引用的概率就越大—这是科学界内马太效应（Matthew Effect）的一个体现[43]。同样，一个学校学科影响力的提高也是论文数量积累到一定阶段的产物。从本文的数据分析来看也有特例，如兰州大学论文数相对较少，但论文的引用率很高，ESI学科排名靠前，主要原因是该校拥某些特别优秀的学科带头人。但从长远来看，十年滚动的数据随时可能将这种效应在下一个周期抹掉。因此，要想学科保持长期、持续和稳定的发展一定要强调论文数量是基础，质量是核心，管理者制定的学科评价标准要落实到考察论文数量与被引次数、高被引论文和热门论文数等多角度体现学科内涵的指标上来。

6.2 重视学科的交叉融合

从高被引文章的院系分布来看，不仅来自数学学院，还有来自其他院系的贡献，并且占比也非常高;从学科领域分支可以看到，数学的学科领域分支多达20多个。数据表明学科正逐渐朝着综合化、集群化的趋势在发展，学科之间的交叉越来越需要得到学科建设者的重视。在高校管理者层面应树立大学科的思想，打破现有学院间学科资源壁垒，建立适应学科综合化发展的管理体制，在资源分配和利用上更加清晰、明确地鼓励学科交叉、合作和融合，组织跨学院相互协作、协同研究，形成合理的学科交叉机制。

6.3 加强国家自然科学基金项目对学科建设的引导作用

通过5所高校基金资助的分析，发现基金项目资助的种类众多，但国家自然科学基金对学科的发展起着最重要的作用。由于国家自然科学基金的设立是突出原创、聚焦前沿，对学科的发展具有引领性和开创的作用，对系统和深入地研究方面起到重要推动作用，促进从事基础研究的科研工作者的快速成长，并催生了大量基础研究。因此对于高校而言，应采取措施鼓励科研工作者积极申报国家自然科学基金项目，应尽量争取国家自然科学基金的支持，助力学术研究。

6.4 聚焦研究前沿，注重与一流科研机构的交流合作

从国内外合作的研究机构的数据可以发现，国内和中科院、国际上和美国等一流高校合作的次数越多，学科影响力也越高。因此，管理层应鼓励研究人员瞄准国内外学科发展前沿，结合自身的研究优势和特点，开展合作研究，特别是与高水平的机构进行合作研究;教育主管部门也需要全盘统筹规划，制定有效的学科规划及合作策略，促进各校之间资源优势互补，保持合作与竞争态势，朝着共同进步的方向发展，促成产出足够数量的有原创性和影响力的高水平成果。

6.5 加强人才队伍的建设

从师资队伍建设的分析中可以看到，从根本上讲，学科的竞争主要是人才的竞争，学科的影响力很大程度上是由该学科的学术团队在学界的影响力決定的，学科强的高校必定是具有强大的人才队伍。由于受各方面条件的限制，高校之间的发展不平衡是一个客观存在。对于没有先天优势的高校，也不能等和靠，要以“双一流”建设为契机，加强人才队伍建设。一是内部培养，注重培养身边的中青年人才，充分调动他们的科研积极性，可以通过国内、国际学术研究讨会的方式，开阔眼界，加强学术交流和合作，鼓励思维碰撞，激发科研新思路;在职称评定方面，对有科研潜力的人才可以开通绿色通道，直接申报高级职称，激励优秀青年人才脱颖而出。二是外部引进，着力引进一批符合学科发展方向、具有国际竞争力的优秀人才，以此加强学科发展的优势或者弥补学科研究空白。

6.6 进一步加强电子馆藏资源的建设

通过5校的馆藏资源的调查，发现各校对数学学科的核心馆藏保障并非全覆盖。高校应围绕“双一流”建设，以服务教学与科研为中心，加强核心馆藏资源建设。根据重点学科的需要，通过和院系专家的沟通、交流，和世界一流大学和一流学科的资源比对，分析支撑教学、科研的资源保障情况，建设重点学科的核心资源，特别是加强电子资源馆藏建设，方便师生利用，这也是目前国内高校在面临不断上涨的学术资源费用与总体投入经费不足的现状时，保障学科建设的有效途径之一。

总之，随着大数据时代的到来，利用各种计量分析工具，对海量数据进行深入挖掘，从而揭示各学科发展的现状，提升学科竞争力，是学科服务工作未来研究与探讨的方向。本文基于ESI数据的数学学科竞争力分析和研究，在一定程度上揭示了各校学科研究特征和未来发展的趋势，为高校数学学科的特色发展、融合发展、合作发展提供了指导。本研究下一步还将结合其他方法，如Incites、SciVal等不同科研和绩效分析工具进行分析，同时将科研经费投入产出状况、科研团队的合作网络、人员建设及其流动影响因素考虑进去，不断印证和充实研究结论。

参考文献

[1]国务院.国务院关于印发统筹推进世界一流大学和一流学科建设总体方案的通知：国发（2015）64号[EB/OL].http：//www.gov.cn/zhengce/content/2015-11/05/content_10269.htm，2015-11-05.

[2]郭战伟.高校进入ESI学科策略研究[J].中国高校科技，2017，（5）：45-47.

[3]武汉大学.重磅|《武汉大学世界一流大学建设方案》正式发布[EB/OL].http：//www.sohu.com/a/217395306_355701，2018-01-18.

[4]李健宁.高等学校学科竞争力评价研究[D].上海：华东师范大学，2004.

[5]唐琳，王纬超.国内外顶尖高校学科竞争力比较研究[J].高等理科教育，2018，（3）：36-42.

[6]邱均平，孙凯.基于ESI数据库的中国高校科研竞争力的计量分析[J].图书情报工作，2007，（5）：45-48.

[7]陈淑云，杜慰纯，秦小燕.中美“常春藤”高校学科对比分析——基于高水平论文的计量学分析[J].图书情报工作，2011，55（8）：44-48，78.

[8]Ge Y.Analysis and Research on the Influence of University Discipline Based on Incites and ESI[A].Proceedings of the 2018 8th International Conference on Management，Education and Information（MEICI 2018）[C]//Available Online December，2018.

[9]Anthipi P，Anastassios P.Competing in a Globalising World：International Ranking of South African Universities[J].Procedia-Social and Behavioral Sciences，2010，2（2）：515-520.

[10]2018年11月ESI數学学科排名[EB/OL].https：//esi.incites.thomsonreuters.com/IndicatorsAction.action？Init=Yes&Src App=IC2LS&SID=J3-V6pTK17ax2F7axxj23qx2FDjdCxxVSGWns GFUI-18x2dhbRknpEDJbPsoix2BefrHXeAx3Dx3DZ7LmfENYjoNa BVhsjW4n9gx3Dx3D-9vvmzcndpRgQCGPd1c2qPQx3Dx3D-wx2BJ Qh9GKVmtdJw3700KssQx3Dx3D，2018-11-16.

[11]邱均平，杨思洛，宋艳辉.知识交流研究现状可视化分析[J].中国图书馆学报，2012，38（2）：78-89.

[12]王颖鑫，黄德龙，刘德洪.ESI指标原理及计算[J].图书情报工作，2006，（9）：73-75，35.

[13]李茂茂，张子倩，陈仕吉，等.基于ESI的中国农业大学植物与动物科学学科竞争力分析[J].科技管理研究，2012，32（8）：128-132.

[14]李洁，陈振英.共引分析视角下的交叉学科领域竞争优势发现研究[J].图书馆研究与工作，2017，（6）：55-60.

[15]吴若溪，孙瑞英.我国信息生态研究的基金资助情况分析——基于论文产出的基尼系数研究[J].现代情报，2015，（6）：13-19.

[16]国际在线.遵循教育规律，建设一流大学[N/OL].北京青年报.http：//baijiahao.baidu.com/s？id=1599426506649279698& wfr=spider&for=pc，2018-05-03.

[17]金炬，武夷山，梁战平.国际科技合作文献计量学研究综述——《科学计量学》（Scientometrics）期刊相关论文综述[J].图书情报工作，2007，51（3）：63-67.

[18]林强.世界一流目标下我国图情学科国际论文产出情况对比分析[J].图书馆工作与研究，2018，（10）：88-94.

[19]Chang K C，Pearson K，Zhang T.Perron-Frobenius Theorem for Nonnegative Tensors（vol 6，pg 507，2008）[J].Communications in Mathematical Sciences，2012，10（3）：1025.

[20]Chen S X，Qin Y L.A Two-sample Test for High-dimensional Data with Applications to Gene-set Testing[j].Annals of Statistics，2010，38（2）：808-835.

[21]Wang H S，Li B，Leng C L.Shrinkage Tuning Parameter Selection with a Diverging Number of Parameters[J].Journal of the Royal Statistical Society Series B-Statistical Methodology，2009，71（3）：671-683.

[22]Wang H S，Xia Y C.Shrinkage Estimation of the Varying Coefficient Model[J].Journal of the American Statistical Association，2009，104（486）：747-757.

[23]Wang H S.Forward Regression for Ultra-high Dimensional Variable Screening[J].Journal of the American Statistical Association，2009，104（488）：1512-1524.

[24]Deng W H.Finite Element Method for the Space and Time Fractional Fokker-planck Equation[J].Siam Journal on Numerical Analysis，2008，47（1）：204-226.

[25]Tian W Y，Zhou H，Deng W H.A Class of Second Order Difference Approximations for Solving Space Fractional Diffusion Equations[J].Mathematics Of Computation，2015，84（294）：1703-1727.

[26]Huang Y M，Ng M K，Wen Y W.A Fast Total Variation Minimization Method for Image Restoration[J].Multiscale Modeling & Simulation，2008，7（2）：774-795.

[27]Zheng B，Bai Z Z，Yang X.On Semi-convergence of Parameterized Uzawa Methods for Singular Saddle Point Problems[J].Linear Algebra and Its Applications，2009，431（5-7）：808-817.

[28]Wang Z C，Li W T，Ruan S G.Traveling Fronts in Monostable Equations with Nonlocal Delayed Effects[J].Journal of Dynamics and Differential Equations，2008，20（3）：573-607.

[29]He X M，Zou W M.Infinitely Many Positive Solutions for Kirchhoff-type Problems[J].Nonlinear Analysis-theory Methods & Applications，2009，70（3）：1407-1414.

[30]He X M，Zou W M.Existence and Concentration Behavior of Positive Solutions for a Kirchhoff Equation in R-3[J].Journal of Differential Equations，2012，252（2）：1813-1834.

[31]Ma L，Zhao L.Classification of Positive Solitary Solutions of the Nonlinear Choquard Equation[J].Archive for Rational Mechanics and Analysis，2010，195（2）：455-467.

[32]Chu J F，Nieto J J.Impulsive Periodic Solutions of First-order Singular Differential Equations[J]. Bulletin of the London Mathematical Society，2008，40（1）：143-150.

[33]Cai T，Liu W D，Luo X.A Constrained l（1） Minimization Approach to Sparse Precision Matrix Estimation[J].Journal of the American Statistical Association，2011，106（494）：594-607.

[34]Ma W X，Zhu Z N.Solving the（3+1）-Dimensional Generalized KP and BKP Equations By the Multiple Exp-function Algorithm[J].Applied Mathematics and Computation，2012，218（24）：11871-11879.

[35]Zhang X Q，Burger M，Osher S.A Unified Primal-dual Algorithm Framework Based on Bregman Iteration[J].Journal of Scientific Computing，2011，46（1）：20-46.

[36]Xu Y Y，Yin W T，Wen Z W，et al.An Alternating Direction Algorithm for Matrix Completion with Nonnegative Factors[J].Frontiers of Mathematics in China，2012，7（2）：365-384.

[37]Cai T，Liu W D.Adaptive Thresholding for Sparse Covariance Matrix Estimation[J].Journal of the American Statistical Association，2011，106（494）：672-684.

[38]Liu L.Precise Large Deviations for Dependent Random Variables with Heavy Tails[J].Statistics & Probability Letters，2009，79（9）：1290-1298.

[39]Gao F Q.Pathwise Properties and Homeomorphic Flows for Stochastic Differential Equations Driven by G-brownian Motion[J].Stochastic Processes and their Applications，2009，119（10）：3356-3382.

[40]Zhou Q，Zhu Q P，Savescu M，et al.Optical Solitons with Nonlinear Dispersion in Parabolic Law Medium[J].Proceedings of the Romanian Academy Series A——Mathematics Physics Technical Sciences Information Science，2015，16（2）：152-159.

[41]Wang Y X，Fan Q B.The Second Kind Chebyshev Wavelet Method for Solving Fractional Differential Equations[J].Applied Mathematics and Computation，2012，218（17）：8592-8601.

[42]趙蓉英，张心源.“双一流”建设背景下中国高校人才与大学排名相关性分析——基于RCCSE2017年中国大学及学科专业评价报告[J].重庆大学学报：社会科学版，2018，24（3）：117-127.

[43]Merton R K.The Mattheweffect in Science.Science，1968，159（3810）：56-63.

（责任编辑：陈 媛）