控制变量法的失当套用例析

唐玉兰 罗国忠

摘   要：控制变量法是一种应用广泛的探究方法，但在教学中存在部分教师不顾实际情况而盲目套用这一方法的现象。在一节课例“探究杠杆平衡条件”中，就存在刻意套用控制变量法的现象，并伴随暗含问题摇摆混同、实际问题主次颠倒、研究变量随意取舍等失当问题。文章针对这些失当问题，提出了改进设想，使问题切合实际，方法有的放矢。

关键词：杠杆平衡条件;控制变量法;套用;主次颠倒

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2020）7-0069-4

控制变量法是非常重要的科学探究方法之一，应用非常广泛，按理说身为教者的教师应该对其使用得心应手。但笔者发现，在教材中没有明示控制变量法之处，有些教师自我发挥，还是会出现一些问题。例如，有些教师不管什么探究内容，总是想方设法把问题设计成“某某与什么有关”“影响某某的因素有哪些”等形式，然后套用控制变量法进行探究，似乎控制变量法是一种万能方法，能探究所有问题，这其实是对控制变量法的夸大、神化而导致的应用失当。

科学史表明，任何研究方法都有其相对应的研究问题和应用规则，没有哪个方法是放之四海而皆准的。因此，本文首先厘清什么是控制变量法？然后以此分析一节课例“探究杠杆平衡条件”，看看这节课例是如何套用控制变量法？由此产生什么问题？

1    什么是控制变量法

在多变量（因素）问题中，一个研究对象可能受到多个变量的影响。为了弄清研究对象与这些变量的关系，我们把多变量问题变成多个单变量问题，首先逐个研究单个变量对研究对象的影响，即每次只改变某一个变量，同时控制其他变量不变;最后把这些单变量结论综合起来，得出总结论。这样的研究方法就是控制变量法，它有如下几个特征。

研究问题。多变量问题的特征比较明显，其标志性形式如“某某研究对象与哪些变量（因素）有关或无关”“如果有关，是什么关系”等。典型例子如“影响滑动摩擦力的因素有哪些”“压强与压力、受力面积有什么关系”等。

研究变量。把可能影响研究对象的变量（因素）称为自变量，而可能受自变量影响的研究对象称为因变量。应用控制变量法时，自变量要互相独立，互不影响。如果有些自变量可能互相影响，则需筛选、排除或整合，这是应用控制变量法的难点之一。

操作程序。控制变量法的操作程序是：一次只改变一个自变量，而其他自变量保持不变。例如，y与x1、x2、x3有什么关系？首先研究y与x1的关系，只改变x1，同时x2、x3保持不变。然后，又依次轮换。

2    一节课例“探究杠杆平衡条件”

下面是一位教师执教“探究杠杆平衡条件”时的探究程序和关键细节[1]。

2.1    问题、猜测

教师让学生相互扳手劲，然后要求学生根据活动“猜出影响杠杆平衡的条件”，并引导学生猜测：①杠杆平衡条件与力的大小、方向、作用点有关;②杠杆平衡条件与力的大小、力臂的长短有关。

2.2    设计、实施

学生猜测后，教师明确要求采用控制变量法，设计探究程序，探究杠杆平衡条件。

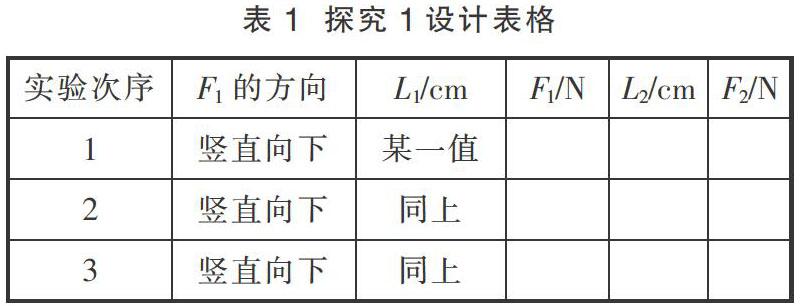
探究1：教师设计表1，探究杠杆平衡条件与作用在杠杆上某个力大小的关系。

具体操作：在杠杆的左端确定一点（L1）挂上钩码，同时在杠杆右端也挂上钩码，直至杠杆重新平衡。然后，在L1不变时，通过增减钩码改变F1的大小，同时在杠杆的右端移动或增减钩码，达到每次改变F1的大小时都能使杠杆平衡。实验进行三次，数据填入表1。教师引导学生得出结论1——当作用在杠杆上的某个力的作用点、方向没有改变，只有大小变化时，杠杆的平衡条件是F1×L1=F2×L2。

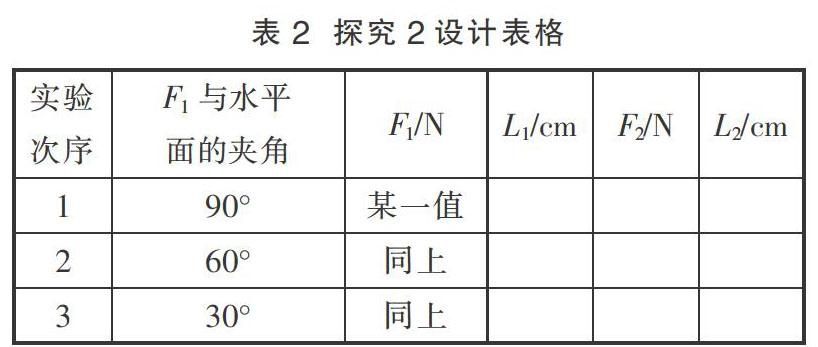
探究2：教师设计表2，探究杠杆平衡条件与作用在杠杆上某个力的方向的关系。

具体操作：类似地，在杠杆的左端确定一点（L1）挂上钩码，同时在杠杆右端也挂上钩码，直至杠杆重新平衡。然后，在F1大小不变时，通过改变钩码与水平面的夹角改变F1的方向，同时在杠杆的右端移动或增减钩码，达到每次改变F1的方向时都能使杠杆平衡。在分析实验数据的基础上，教师引导学生得出结论2——当作用在杠杆上的某个力的作用点、大小没有改变，只有方向变化时，杠杆的平衡条件是F1×L1=F2×L2。

探究3：有了两次经验后，教师让学生自主探究杠杆平衡条件与作用在杠杆上某个力作用点的关系，并得出结论3——当作用在杠杆上的某个力的大小、方向没有改变，只有作用点变化時，杠杆的平衡条件是F1×L1=F2×L2。

总结论：

总结三个分结论，得出总结论：无论作用在杠杆上的某个力的大小、方向、作用点怎样变化，杠杆的平衡条件都是F1×L1=F2×L2。

3    案例存在的问题分析

3.1    暗含问题摇摆变化、相互混同

对于杠杆，初中物理课程标准的目标要求非常明确，即“通过实验，探究并了解杠杆平衡条件”，其知识目标是“杠杆平衡条件”，对应的探究问题就应是“杠杆平衡条件是什么”，这个问题本应贯穿始终，但这节课却还伴随着其他暗含问题，而且摇摆变化，有些甚至相互混同。所谓暗含问题，指教师并不明说，但可以从其要求中推断出来的问题。

在学生扳手劲活动后，教师的最初要求是“猜出影响杠杆平衡的条件”，并引导学生猜测：①杠杆平衡条件与力的大小、方向、作用点有关;②杠杆平衡条件与力的大小、力臂的长短有关。表面上，这里没有明示的问题，但从最初要求“猜出影响杠杆平衡的条件”可以看出，其暗含问题是“影响杠杆平衡的条件是什么”——问题1;从其引导的猜测可以看出，其暗含问题又变成“杠杆平衡条件与哪些变量有关”——问题2。首先，从形式上看，问题1和问题2都是与控制变量法匹配的多变量问题。其次，问题1和问题2并不是同一个问题，因为问题1的因变量是“杠杆平衡”，自变量是“条件”;问题2的因变量是“杠杆平衡条件”，自变量是“变量”。显然，两者的因变量完全不同，自变量也完全不同。但不难看出，教师已经在无意识中把两个问题视为同一个问题，即把“杠杆平衡”当成“杠杆平衡条件”，把“条件”当成“变量”。这显然是概念混同导致了问题混同。

在学生猜测后，教师接着明确要求用控制变量法，设计探究程序，探究杠杆平衡条件。表面上这里也没有明示的问题，但也可以从其要求“探究杠杆平衡条件”看出，其暗含问题变成了“杠杆平衡条件是什么”——问题3，这才是这节课本该研究的正确问题。问题3和问题1、问题2看似差不多，其实差异很大。问题2问“杠杆平衡条件与各个变量的独立关系”，而问题3问“这些变量整体满足什么条件时，杠杆才会达到平衡状态”，因此，问题3和问题2完全不是同一个问题，问题3和问题1也不是同一个问题。

设计探究程序时，在三个变量中（F1的三要素），每次改变一个变量，其他两个变量控制不变。尽管问题也没有明示，但从其设计也可以看出其暗含问题变成了“杠杆平衡条件与力的三要素是否有关”——问题4。问题4和问题2看似差不多，都属于多变量问题，但这里问题4的多变量明确缩减为三个变量（力F1的大小、方向、作用点），而不是原来猜测的五个变量（①力的大小、方向、作用点;②力的大小、力臂的长短）。

实施探究时，采用了控制变量法，根据数据得出三个分结论，并综合成总结论，即“无论作用在杠杆上的某个力的大小、方向、作用点怎样变化，杠杆的平衡条件都是F1×L1=F2×L2”。该结论可分成两部分，分别回答了暗含问题3“杠杆平衡条件是什么”、暗含问题4“杠杆平衡条件与力的三要素是否有关”。

从以上分析看出，这节课本应围绕问题3贯穿始终，但其暗含问题却不断摇摆变化，而且相互混同，缺乏清晰的问题主线。由于这些暗含问题是潜藏的，教师很有可能并未意识到它们的存在及其变化、混同。

3.2    实际问题主次颠倒、喧宾夺主

如果教师未意识到其暗含问题的多变、混同，那么其真正想研究的实际问题究竟是什么呢？不妨分析这节课得出的最终结论（达成的总目标），即“无论作用在杠杆上的某个力的大小、方向、作用点怎样变化，杠杆平衡条件都是F1×L1=F2×L2”，如前面分析，可以看出它回答两个问题，即“杠杆平衡条件是什么”“杠杆平衡条件与力的三要素是否有关”，这就是教师真正想研究的实际问题。

如果一定要研究这两个问题，那么对照课标要求可知，前一个问题毋庸置疑是必须研究的主要问题，后一个问题是可选的次要问题。主要问题本应下重手研究，即应通过实验得出几组“F1、L1、F2、L2”数据，然后对数据进行分析处理，设法找出其潜藏的规律（条件）。但由于数据繁杂，表面看似毫无规律，如果没有提示引导，学生仅凭己力，一般不知道从何着手，难以得到正确结论“F1×L1=F2×L2”。因此，如何引导学生分析、处理数据，历来就是这节课的重点、难点、亮点之一。然而，纵观整个探究过程，看到更多的是教师把心思花在设计并探究其创新点“杠杆平衡条件与力的三要素是否有关”，反倒没有看到如何分析处理棘手的“F1、L1、F2、L2”数据，“杠杆平衡条件”更像是可以轻易附带出来的副产品。

从以上分析看出，教师把课标未作要求的“杠杆平衡条件与力的三要素是否有关”提升为问题主线，把课标要求的“杠杆平衡条件是什么”降格为附属问题并塞进其中，造成了主次颠倒、喧宾夺主的逻辑错位。究其原因，是教师要突出控制变量法的应用，所以就刻意设计并突出“杠杆平衡条件与力的三要素是否有关”问题，这样就能用控制变量法实施探究。这种做法貌似体现了不拘泥于课标和教材的创新精神，殊不知违背了知识逻辑，脱离了实际情况，无异于“削足适履”。

3.3    研究变量随意取舍、缺乏整合

再从研究变量的角度，来看看教师对控制变量法的应用是否适当？

教师引导学生两次猜测：①杠杆平衡条件与力的大小、方向、作用点有关;②杠杆平衡条件与力的大小和力臂的长短有关。接着，明确要求用控制变量法进行研究。那么，按照控制变量法的规则，既然总共猜测了五个变量，接下来就应该探究杠杆平衡条件与这五个变量的关系。但实际上教师却只探究“杠杆平衡条件与某个力（F1）的大小、方向、作用点的关系”，根本不提“杠杆平衡条件与力的大小、力臂的长短的关系”，而且没有任何解释说明。这种做法显然违背控制变量法的应用规则，同时也会给学生示范一个不良行为：研究变量可以随意取舍。

其实，教师引导下的两次猜测结果貌似不同，其实完全相同。因为第一次猜测中的“力的方向、作用点”可整合为“力臂的长短”，这样两次猜测的结果其实完全一样，都是“力的大小、力臂的长短”。但教师却不分析、不整合，硬是掰成两个“不同”的猜测，这样的做法也同样不符合控制变量法的应用规则。

如果联系前面对实际问题的分析，不难看出教师对变量的随意取舍、缺乏整合，其实与实际问题的主次颠倒是一脉相承的。纵观整个探究过程，不难看出教师的设计意图，即把“力的大小、方向和作用点”归口到“杠杆平衡条件与力的三要素是否有关”，把“力的大小、力臂的长短”归口到“杠杆平衡条件是什么”，所以才会把同一个猜测结果硬生生地掰成了两个貌似不同的猜测结果。

4    改进设想

首先，在学生扳手劲活动的基础上，引导猜测可能有哪些因素影响杠杆平衡（不是杠杆平衡条件）？假如学生的确猜测了“①力的大小、方向、作用点;②力的大小、力臂的长短等”，那教师就应该引导学生分析、梳理这些变量，使他们认识到这些变量相互之间并不完全独立，而是可以整合为两个变量：力的大小、力臂的长短，而杠杆所受的力分为动力、阻力，相应力臂分为动力臂、阻力臂。接着，由教师引出新问题“动力、阻力、动力臂和阻力臂在满足什么条件时可以使杠杆平衡”——问题A。要探究问题A，不宜使用控制变量法，而应该用比较法，即比较杠杆平衡时四个变量的整体关系。比较法对操作过程、变量是否控制不作限制，灵活多样，只要出现平衡结果即可，即不管过程只要结果，类似“八仙过海，各显神通”。生活例子比比皆是，如用锤子撬铁钉，属于控制一个量（阻力）不变，变化另外三个量;用杆秤称东西，属于控制两个量（阻力臂和动力）不变，变化另外两个量;锅炉的保险阀门，属于控制三个量（阻力、阻力臂、动力臂）不变，变化另一个量;坐跷跷板，甚至四个变量都同时变化，也能达到平衡。

接着，如果学生的确发自内心提出“杠杆平衡条件与某个力的大小、方向、作用点是否有关”——问题B，那就不妨作为问题延伸进行研究，用证据回应学生的关切，冲击学生的前概念，这也是尊重学生主体地位的体现。这时，就可以像课例中那位教师所做的那样，通过控制变量法进行研究。

在以上设计中，问题A是重点，是保底基础，问题B是延伸、可选，两者指向不同、层次分明;相应的比较法、控制变量法也有的放矢，各為其主，服务各自问题。方法是为问题服务的，不能为了套用某个重要方法而刻意设计与其匹配的探究问题，甚至把真正的主要问题降格为附属问题。那样的“削足适履”既不利于培养学生发现问题、提出问题的能力，也不利于培养学生正确应用科学方法的意识和能力。

参考文献：

[1]魏喜武.“探究杠杆平衡条件”的教学设计[J]. 物理教学，2012，32（1）：36-38.

（栏目编辑    张正严）

收稿日期：2020-03-10

作者简介：唐玉兰（1963-），女，中学特级教师，主要从事中学物理教学研究，享受政府特殊津贴;罗国忠（1968-），男，教授，主要从事中学物理教学研究。