人工智能技术与存贷款指标预测——基于改进支持向量机回归模型

陈 杰

（中国人民银行重庆营业管理部，重庆渝北 401147）

重要经济金融指标数据的准确预测是决策者判断和制定相应政策的重要参考依据。存贷款数据是金融统计工作中的基础性指标，也是分析金融运行环境的关键性指标，在很大程度上会反映金融自身的“造血”能力以及对实体经济的支持力度，在国民经济金融统计中有着极其重要的地位。因此，对存贷款指标数据进行预测，可以为各级政府部门、金融监管部门的前瞻性调控奠定基础，也可以引导金融市场合理预期，对进一步完善各项金融工作、合理引导市场预期等具有重要的理论意义和现实意义。

一、文献回顾

金融预测指运用数据挖掘的方法对金融市场的大量历史数据进行处理和分析，以此预测市场的未来发展趋势。金融指标历史数据属于时间序列数据，通常存在非平稳现象，若根据时间序列本身的趋势变化来预测，最常用的预测方法可采用简单平均法、移动平均法、指数平滑法等构建预测模型，也可采用自回归模型（AR模型）等进行预测分析；若时间序列包含可观测影响因素，一般采用回归方法构建模型，如一般线性回归、自回归滑动平均模型（ARMA模型）等。

机器学习是人工智能研究发展到一定阶段的必然产物，随着机器学习理论与实现算法的不断进步和发展，机器学习将在未来改变经济学的研究方式，并对经济学的研究和发展产生深远影响。

机器学习大致可以分为四类：有监督机器学习、无监督机器学习、半监督机器学习和强化机器学习。有监督机器学习主要解决预测问题，拥有输入变量（自变量）和输出变量（因变量），使用被标注过的样本数据，通过学习特征与标签值间的对应关系，构建最优模型进行预测，常用方法包括回归树、支持向量机、神经网络等方法。无监督学习主要解决聚类问题，只有输入变量，没有相关的输出变量，通过样本集合中的特征，来发现和识别出代表性特征，并对预测数据进行聚类，常用于视频、图像和文本数据领域。半监督机器学习使用大量的未标记数据，以及同时使用标记数据，来进行模式识别，常用的包括协同训练、转向支持向量机等方法。强化机器学习主要应用到人工智能领域，它并不只是使用已知固定的数据进行训练，而是通过大量试错练习，寻找最佳路径选择。

机器学习在经济金融领域尚未大量展开，在部分领域进行了初步探索，还处于起步阶段。在经济领域，Chalfin et al（2016）利用教师的知识水平、教学方式，以及学校教学评估的大量信息，用机器学习方法预测个人的劳动生产率。Peysakhovich & Naecker（2017）研究了人们在面对金融市场风险时的选择行为，预测效果较为准确。在金融领域，大部分是对股票市场的预测。Gu et al（2018）使用美国3万多只股票在1957-2016年间的数据来预测股票的未来收益，作者发现，在预测具有高流动性的股票或投资组合的未来收益时，机器学习方法比传统的预测方法更加有效。在国内，孙存一（2017）以机器学习视角研究了利率定价机制，研究表明，大数据机器学习方法对相当时期的利率变动能够精准地预测。景秋玉（2018）结合机器学习方法，基于PCA-SVM-GARCH模型建立股价预测模型，梁成（2018）基于小波核支持向量机回归方法建立股指期货价格预测模型，均取得较好预测效果。

本文将机器学习方法从股票高频数据运用到存贷款低频数据，是对人工智能技术在金融预测领域的创新性尝试；同时与以往传统方法相比，机器学习又具有诸多优点，能够自动搜寻符合预测要求的自变量最优交互项组合，这是传统方法无法做到的。

二、支持向量机学习方法

有监督机器学习方法的出发点是构建一个损失函数，基于该损失函数，通过代入训练数据来选择最优的预测模型，这与传统最小二乘法类似。但与传统计量经济学方法不同的是，比如在一般线性回归模型框架下，机器学习算法能够允许损失函数忽略掉模型输入与真实输出之间很小的偏差，也能自动搜寻自变量最优交互项组合以满足模型的更多需求。支持向量机方法是最常用的有监督学习算法之一，在各个预测领域被广泛应用，它有多方面的优点：一是支持向量机使用结构风险最小化准则在特征空间寻找最优分类超平面，模型通过二次型进行优化，能够获得全局而不仅仅是局部最优解。二是支持向量机是基于有限样本求取有限信息下的最优解，在处理小样本问题也具有很好的效果。三是对于线性不可分问题，模型将低维空间数据变换为高维特征向量，通过非线性转换将非线性问题转变为高维空间中的线性问题，然后在高维特征空间构造最优分类超平面，很好地解决了高维数据的非线性分类问题。四是支持向量机模型中引入核函数理论，简化高维空间中特征向量内积的计算，解决了在扩维引发的维数灾难问题。

（一）支持向量机基本模型

（2）式即为支持向量机的基本型。为求解，通常考虑其如下的对偶问题：

求解该式可得到最优划分超平面所对应的模型：

在求解过程中，要将样本空间映射到更高维特征空间，可采用核函数升维，常用的核函数有线性核、多项式核、高斯核、拉普拉斯核、Sigmoid核等。

（二）改进的支持向量机回归模型

传统的支持向量机回归模型只能通过影响因素预测当期数据，这并不能充分满足我们的预测需求。我们对其加以改进，得到改进的支持向量机回归模型，能够通过截至期数据预测期之后的数据，从而达到预测目标。

支持向量机回归模型与分类模型建模基本思路一致，但主要解决预测问题。这里，我们采用改进的支持向量机回归方法。给定一个训练集，其中，是输入向量，表示第个观测值，为输出变量，通过期及之前的数据训练得出期数据，即为预测下一期数据。采用方法对数据进行训练学习，支持向量回归基本优化模型如下：

其对偶问题为：

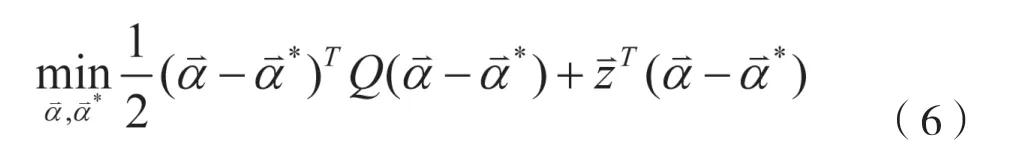
三、预测模型设计和实证分析

（一）预测模型设计

在实体经济金融运行过程中，影响存贷款的因素有很多，从宏观上看，既受实体经济运行大环境的影响，也受国家宏观政策和监管政策的指导；从中观上看，既受金融市场直接融资的影响，也受房地产等行业发展阶段的影响；微观上看，既受住户的消费等个人因素影响，也受企业自身发展有效需求的制约。根据数据有效性和可获得性，选取10个指标作为影响存贷款的主要因素，并且采用月度数据进行训练。其中，由于GDP通常是季度数据，采用工业增加值月度同比数据替代，反映实体经济大环境的基本面情况；M2同比增速、人民币存款准备金率、短期贷款利率主要反映货币政策和货币环境，可部分反映货币供给端和需求端的情况，为更直接反映利率对贷款的影响，选取6个月至1年(含)短期贷款利率；股票流通市值、债券市场托管余额可部分反映金融市场对资金的吸引程度，以及直接融资等基本情况；CPI同比增速、70个大中城市新建商品住宅价格指数同比增速反映普通物价消费情况和房地产市场的冷热程度；定期存款利率：1年，反映单位和个人存款的获利程度；外汇储备，外汇占款会部分在存款中体现（表1）。在存款预测中，影响的主要因素包括序号为1-3，5-10共9个指标；贷款预测中，影响的主要因素包括序号为1-8共8个指标。

表1 影响存贷款的主要因素

（二）实证结果分析

本文采用2015年以来的全国存贷款等公开数据进行模拟训练和实证分析，选择高斯核函数，通过对已有截至期的存贷款余额数据，对往后期的存贷款余额进行预测，实证中期为2019年2月末，整个实证在python3.7和keras环境下实现。参数选择及实证结果见表2、表3、表4。

从实证结果看，各期预测结果很好，预测值和实际值的绝对误差较小，相对于各项存款和各项贷款分别约190万亿和150万亿的体量来说，各项绝对误差相当小，各项存款和各项贷款平均绝对误差分别为4393亿元和3772亿元，相对误差几乎全部在0.5%以内，有的甚至小于0.1%，各项存款和各项贷款的平均相对误差也分别仅为0.23%和0.25%。可以看出，我们的预测结果很好地反映了真实情况，具有很强的预测能力，预测值完全可以作为经济金融分析工作的一项重要参考，具有重要的前瞻性指引和实践指导意义。

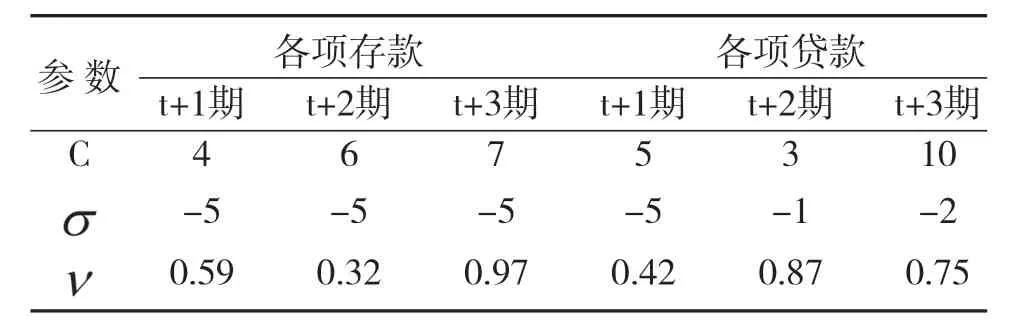
表2 预测中参数值

表3 2019年各项存款预测结果表 单位：亿元

表4 2019年各项贷款预测结果表 单位：亿元

四、结论

传统时间序列模型仅从自身历史数据出发，没有考虑到宏观经济与政策等因素影响，导致预测结果出现一定偏差，而一般回归模型又较难刻画影响因素之间复杂的内在逻辑关系，传统的支持向量机回归模型也只能预测当期数据而不能实现“真正”的预测目标。我们通过改进传统支持向量机回归模型，在机器学习中创造性的实现了用期数据对期数据的预测，实证结果显示，预测结果精度高，预测值的绝对误差和相对误差都相当小，能够满足各方对金融统计数据的前瞻性需求。