改进免疫遗传算法的篦冷机二次风温故障诊断
2020-08-14刘浩然张力悦刘永记范瑞星
刘浩然,张力悦,刘永记,范瑞星,刘 彬
(燕山大学信息科学与工程学院,河北秦皇岛 066004; 燕山大学河北省特种光纤与光纤传感重点实验室,河北秦皇岛 066004)
1 引言
贝叶斯网络是描述不确定性的概率性手段,由节点集、有向边、条件概率表组成,通过图论和概率论相结合的方法来表述数据间的相互联系,在数据挖掘、故障诊断领域具有较为广泛的应用[1].
贝叶斯网络学习包括结构学习、参数学习,由结构和数据可以确定参数,所以结构学习一直是贝叶斯网络研究的重点[2].构建贝叶斯网络结构最常见的方法是基于评分搜索的方法,该方法的两个关键是评价函数的选取与搜索策略的选择.目前搜索方法主要有蚁群算法[3]、细菌觅食算法[4]、遗传算法[5]等元启发算法.刘浩然等将最大支撑树与爬山算法结合提出简化爬山算法(simplify hill-climbing,SHC)[6],该算法在缩短时间上有一定的提升,但仍有许多冗余边产生,寻找效率也有待提升.刘宝宁等人将遗传算法引入贝叶斯结构学习中,利用邻接矩阵的寻优区域作为初始种群,使用交叉和变异算子寻找最佳的贝叶斯网络结构[7].但由于无法确定遗传算法何时搜索到最优结构,初始种群的规模通常设置很大,导致算法运行时间过长.Vafaee F等基于独立性测试与遗传算法提出了基于遗传的混合结构算法(hybrid structure learning using genetic algorithm,HSL–GA)算法,先利用独立性测试限制搜索空间,然后结合遗传算法搜索最优贝叶斯结构[8],与爬山算法相比搜索效率更高,但是单一的交叉与变异算子不能根据具体情况对个体进行自动调整,易破坏种群的多样性而陷入局部最优.Contaldi C等提出了基于精英遗传自适应的算法(adaptive elite-based structure learner using genetic algorithm,AESL–GA)算法,该算法采用自适应的控制参数来避免参数设置对结果的影响,在小网络中学习到了较优的网络结构,但在大网络中由于缩小搜索空间导致学习的结果不太理想[5].遗传算法的局部搜索能力较差[9],许多学者通过引入爬山算法优化遗传算法的搜索,但并没有从根本上提升局部搜索的能力.
针对上述现状,提出一种改进遗传算法(improved immune genetic algorithm,IIGA).该算法使用最大支撑树和评价函数组成双初始种群,在群内引入改进免疫策略和自动交叉变异策略:种群内的每个个体根据具体情况自动选择免疫位数,交叉和变异方式;在群间引入改进的联姻策略和师生交流机制,即选取两个种群内的部分优秀个体进行联姻,选取联姻后更优秀个体与各种群内部的较差个体进行师生交流.IIGA改善了遗传算法(genetic algorithm,GA)算法应用于贝叶斯网络结构学习时耗时较长,易收敛于局部最优的问题.
2 IIGA算法
2.1 IIGA算法构建
由数据样本计算当前贝叶斯网络所有节点之间的互信息,通过互信息得到最大支撑树,并将其设为初始状态S1.互信息作为变量之间关系的衡量标准,而最大支撑树作为以互信息得到的树形结构[10].假设存在变量X和Y,其互信息I(X,Y)表示为

式中:p(X,Y)为X和Y 的联合概率;p(X),p(Y)分别为X,Y 的边缘概率.
将初始状态S1代入式(2)得到状态S2


图1 一步状态转例图Fig.1 One step state transition diagram
将S1,S2代入式(3)得到其对应的适应度值f1,f2.若f2>f1则将S2储存到初始种群G2,S1存储至初始种群G1,并利用式(4)所示接受状态转移即将S2转移到S1,否则将拒绝状态转移.重复该过程直到得分不再增加.由此构建两个初始种群G1,G2.
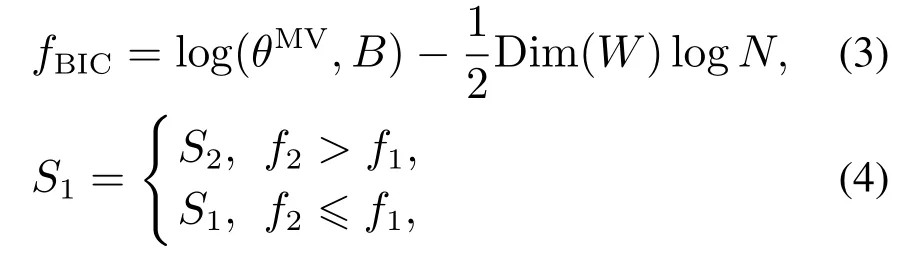
式中: θMV为参数的最大似然估计;Dim(W)为网络结构B的维数;N为输入的数据样本量;n为节点个数;f1为S1的适应度值;f2为S2适应度值.
种群G1,G2内使用邻接矩阵表示贝叶斯网络结构,具体如图2所示.
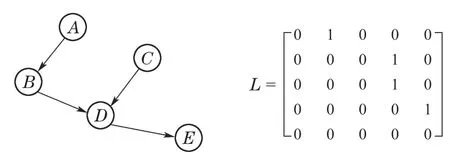
图2 贝叶斯结构例图Fig.2 Example of Bayesian structure
文献[11]提出的自适应免疫遗传算法,将免疫算法的最优特性与自适应遗传算法进行混合,改进了算法的全局寻优能力.本文为了自适应调整种群G中每个个体的免疫位置,对文献[11]算法进行改进,将自适应因子引入免疫算子,根据种群内的个体的分布情况构建自适应的免疫算子σ,如式(5)所示.在算法的迭代初期种群的个体分布较为分散即大部分个体与最佳个体的距离较大,因而阈值σ较小,但随着迭代的进行种群的个体分布趋于集中即较多个体分布于最佳个体周围,因而阈值σ逐渐增大.

式中: fmax为种群的最佳适应度,为大于种群平均适应值个体的平均值.
将式(5)代入式(6)建立了种群G的自适应免疫算子,即当种群G内个体评分f(Gl)与最佳评分fmax之间的差距小于阈值σ时,Gl与通过与操作确定免疫位置,否则Gl与通过与操作确定免疫位置.

式中:G表示初始种群,Gl表示种群中的个体.IM1(·)表示Gl与中元素同时为1的位置,IM2(·)表示Gl与中元素同时为1的位置.由上式可以知道IM1(·)免疫位数较多,可保证个体优良特性;IM2(·)免疫位数较少,可以增加种群多样性.
将G1,G2代入式(7),得到免疫后的结构空间NG1,NG2.
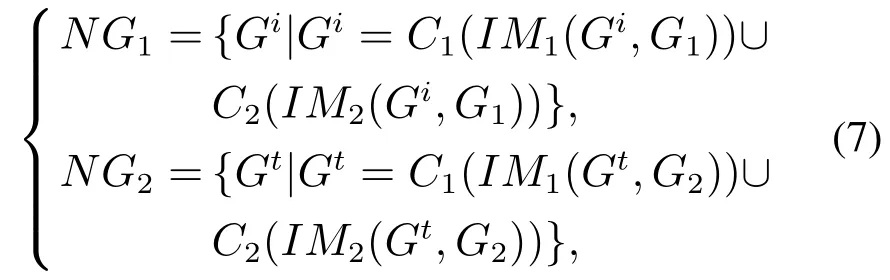
式中:Gi(i1,2,···)表示G1中的随机个体,Gt(t1,2,···)表示G2中的随机个体.C1(·)表示IM1免疫操作后个体集合,C2(·)表示IM2免疫操作后的个体集合,∪表示两个集合的并集.
在NG1,NG2内部引入自适应免疫遗传算法[11]中的自动交叉变异算子,由于在迭代初期,个体的差异较大,采用两点交叉就可获得较广的搜索空间;而在迭代后期,个体差异较小,需要采用两点变异扩大搜索空间.因而根据当代种群个体之间的相对值构建如式(8)控制交叉与变异操作的阈值µ.

将式(8)代入式(9)得到自动交叉变异算子,若个体得分sc>µ则进行两点交叉,增快种群收敛;若个体得分scµ则进行两点变异,保持个体具有大部分优良基因,并以一定概率产生更好的个体,提升全局搜索的能力.
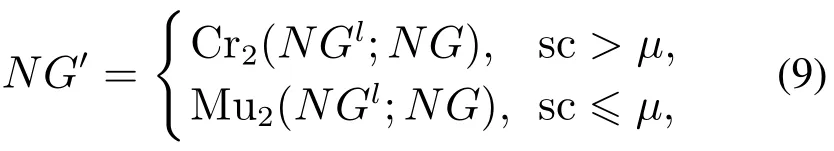
式中:Cr2(·)为两点交叉函数;Mu2(·)为两点变异函数;NG为结构空间;NGl为结构空间内任意个体.
在执行交叉算子和变异算子过程中,个体(邻接矩阵)的两点交叉是将两个矩阵的双行或双列之间进行交换,个体(邻接矩阵)的两点变异是将位于同矩阵的单行内的两元素取反.如图3为两点交叉,即将矩阵M和矩阵N的第4列和第5列进行交换得到矩阵P;图4为两点变异,即将矩阵Q的第4列和第5列的第1个元素进行取反得到矩阵V.
将式(7)得到免疫后的结构空间NG1,NG2的个体代入式(10),可得更新之后的结构空间
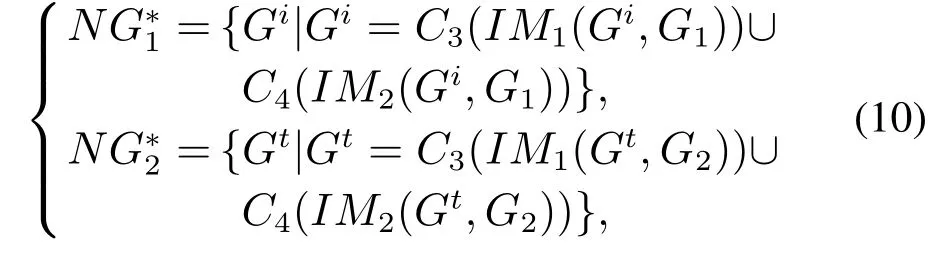
式中:C3(·)是两点交叉后的新个体集合,C4(·)是两点变异后的新个体集合.

图3 两点交叉操作Fig.3 Two point crossing operation

图4 两点变异操作Fig.4 Two point mutation operation
文献[12]在遗传算法的基础上提出联姻策略[12],通过提升子种群间的信息交互能力,改善了遗传算法局部搜索的能力.更新结构为之后,为了提高其局部搜索能力构建了改进联姻策略,即先选取中优于得分Fscore−u的优秀个体执行联姻操作,即利用式(11)将评分高于Fscore−u的个体存放在集合d1.

式中:MF(·)为联姻函数;G3−score为联姻后的个体得分;Fscore−u为种群中两个最佳评分中的较小值.C5(·)是联姻策略后的新个体集合,C6(·)是新个体评分高于Fscore−u的个体集合,∩是两个集合的交集.对联姻策略的改进改善了原联姻策略执行复制后两种群中个体多样性减少的问题.
为提高算法全局搜索的能力,IIGA算法在子种群中引入师生交流机制[13],即将联姻策略得到的新个体作为师生交流机制中的教师种群Te,选取中较差个体作为学生种群St.搜索第k个教师Tek和第l个学生Stl的差异边添加至学生Stl,经过此学习过程,得到更新的学生实现了师生交流,具体如式(12)所示:
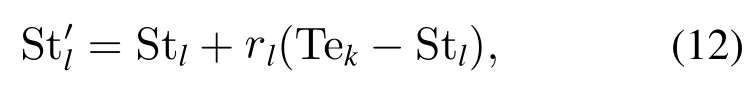
式中:Stl是第l个的学生,Tek为第k个老师,为更新后的贝叶斯结构,控制参数rl为第k是根据式(13)确定.
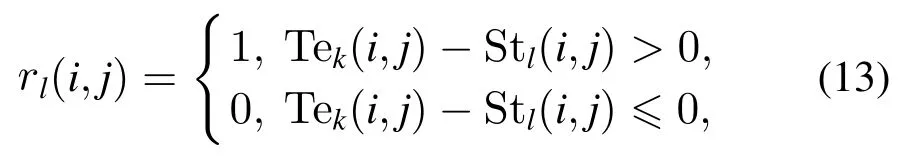
式中:Tek(i,j)表示的是教师Tek第i 行第j列的取值,Stl(i,j)表示的是学生Stl具体位置的取值,rl(i,j)表示的是控制参数rl具体位置的取值.
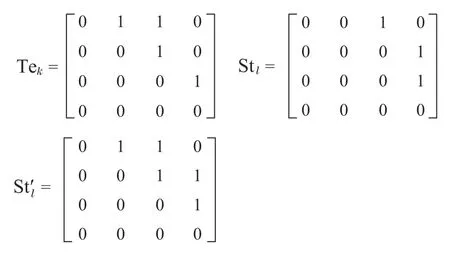
图5 师生交流机制Fig.5 Teacher-student communication mechanism
对更新后的学生种群St′进行优化.从St′中随机选择两个贝叶斯结构并且通过评分低的个体向评分高的个体学习,以保证下一代种群中的个体具有上一代的优良基因.若f根据式(14)更新个体,否则根据式(15)更新个体.
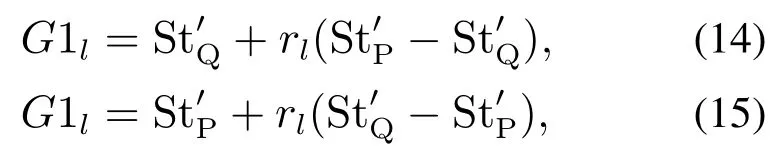
式中: G1l表示优化之后的贝叶斯网络结构. f(G1l)为G1l的评分,如果f(G1l)>f并且f(G1l)>将G1l作为最优结构进行下一次迭代.将学习到的较佳结构保存到集合St中.
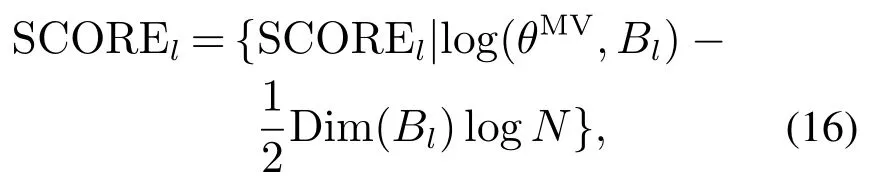
式中Bl分别代表结构集合,St.
将具有群内和群间的最高评分的个体进行比较得到最终的最高评分的个体(即贝叶斯网络结构G∗),如式(17)所示:

2.2 IIGA算法收敛性分析和时间复杂度分析
2.2.1 IIGA算法收敛性分析
引理1IIGA算法的最优解空间Sgbest的概率测度大于0,即L[Sgbest]>0.
证已知IIGA算法的贝叶斯结构群搜索空间S是可列集.显然它的Lebesgue[14]总是大于0,即L[S]>0,其中IIGA 算法的最优解空间Sgbest是属于S 的一个Borel[14]子集,由IIGA算法的最优解空间Sgbest的定义可知L[Sgbest]>0[15].证毕.
引理2IIGA算法中,当满足了L[Sgbest]>0时,式(18)成立:
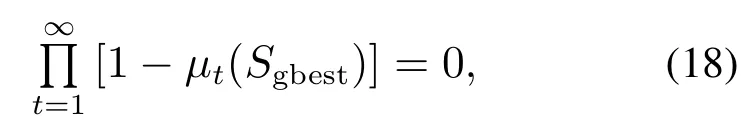
式中µt(·)为第t次迭代结果的概率测度.
证当满足L[Sgbest]>0时,有0<µi,t(Sgbest)<1,可知由µt产生的对Sgbest的概率测度为
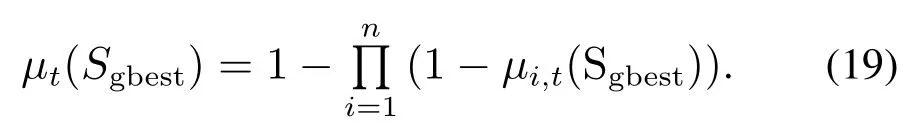
将式(19)代入式(20)可得
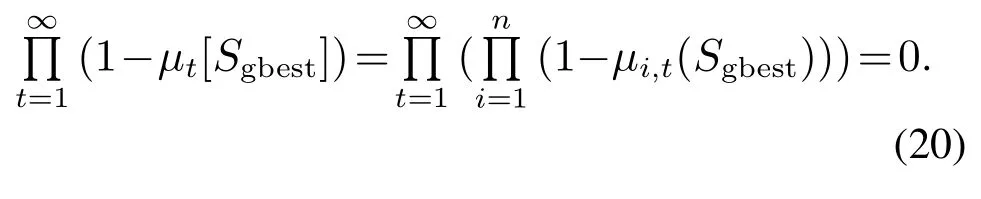
证毕.
根据引理1–2以及随机搜索算法的收敛准则[16]可知IIGA算法满足式(21):

2.2.2 IIGA算法时间复杂度分析
假设在IIGA算法中,n表示贝叶斯节点数,m表示样本数,M表示种群规模,t表示迭代次数,则建立最大支撑树的时间复杂度为O(n2)+O(2mn),进行加边、减边、转变一步状态转移的时间复杂度为O(3n),评分函数的时间复杂度为O(mn2),状态转移S2到S1的时间复杂度为O(2M),故种群初始化的时间复杂度为O(n2)+O(2mn)+O(3n)+O(mn2)+O(2M)O(m×n2);最佳适应度的时间复杂度为O(M),计算种群适应度的时间复杂度为O(Mn2)+O(mn2);免疫算子改进的时间复杂度为O(Mn),自动交叉和变异算子的时间复杂度分别为O(2Mn2)和O(Mn);联姻策略的时间复杂度为O(Mm),师生交流机制的时间复杂度为O(Mn2);因此结构寻优过程的时间复杂度表示t[O(M)+O(Mn2)+O(mn2)+O(Mn)+O(2Mn2)+O(Mn)+O(Mm)+O(Mn2)]O(t×(M +m)×n2)IIGA算法的时间复杂度为O(n2(t×(M +m)+m)).
2.3 IIGA算法实现步骤
上节详细介绍了IIGA算法的收敛性分析,本节对IIGA算法的整体实现过程进行描述,实现过程如下:
1)输入网络数据,计算互信息,构建最大支撑树作为初始状态S1,计算评分,设置Nc1,最大迭代次数Ncmax;
2)使用爬山算法的加边算子,减边算子和转变算子对初始状态进行结构变换,将变换后的状态记为转移状态S2;
3)判断S2>S1,若成立,则存储S2至G2,存储S1至G1,同时将S2标记为当前状态S1并转步骤2),否则拒绝状态转移转步骤2),重复该过程直到评分不再增加,由此构初始种群G1,G2;
4)根据改进的免疫策略和自动交叉变异机制将G1,G2中的个体进行免疫、交叉、变异操作,得到结构集合
6)执行师生交流机制更新St;
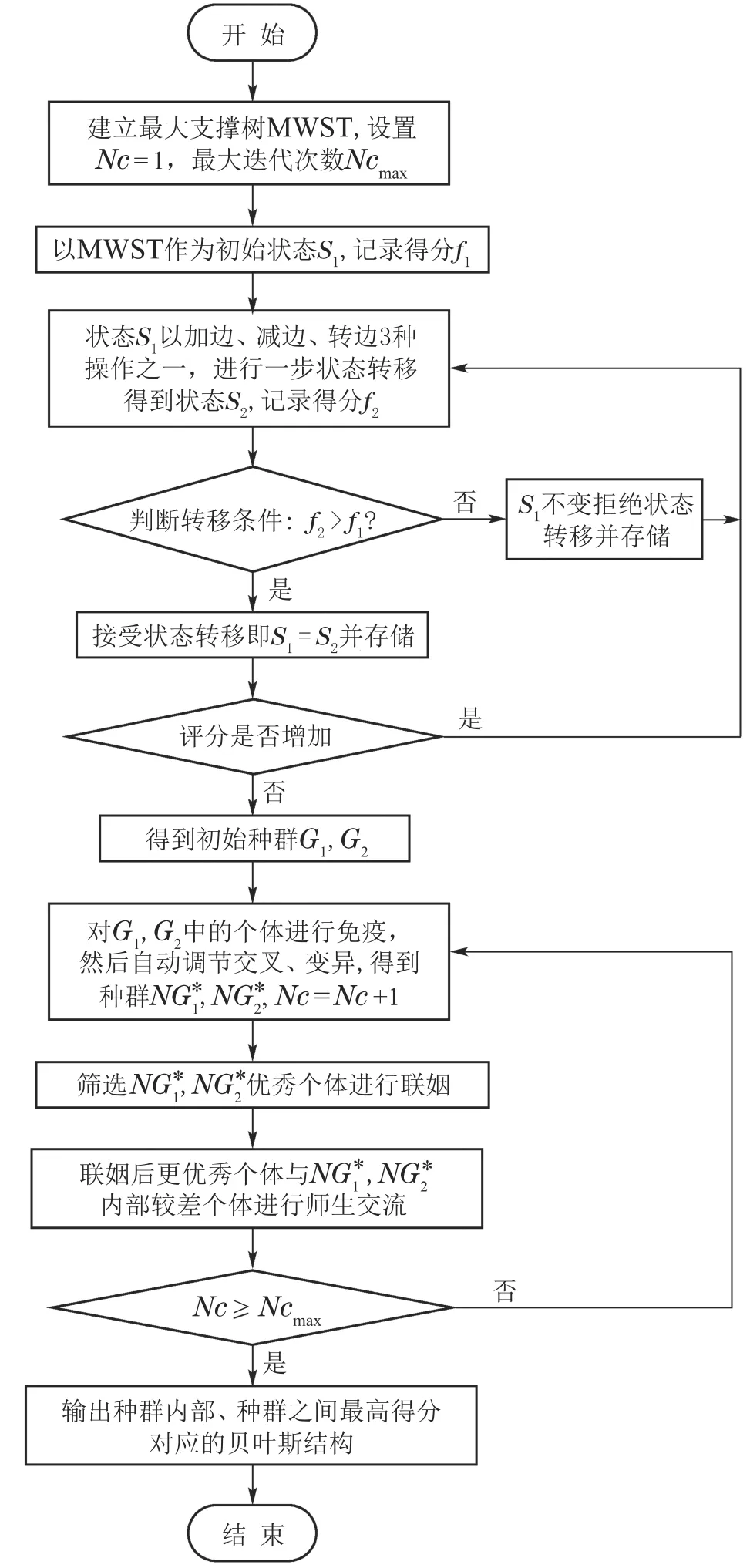
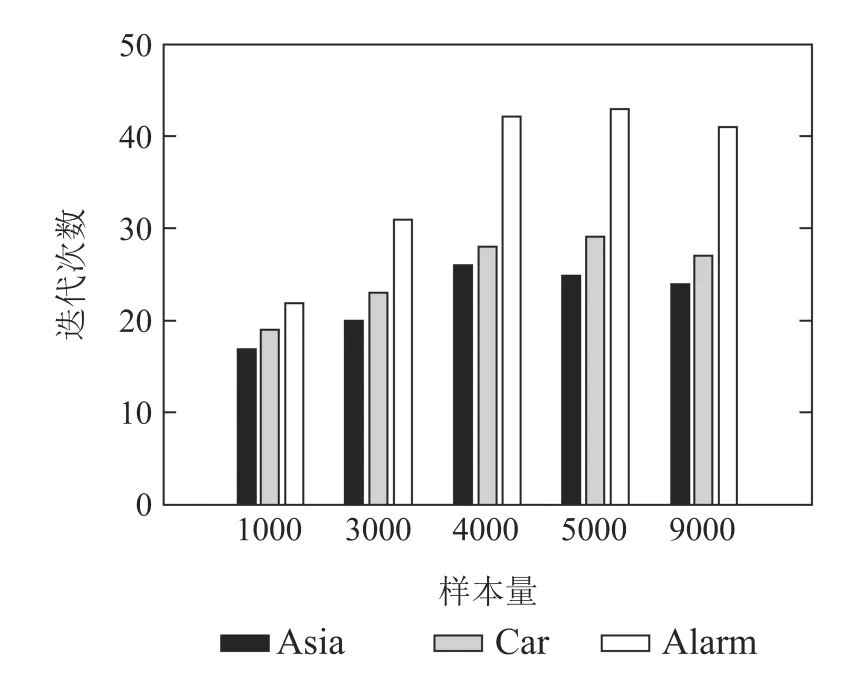
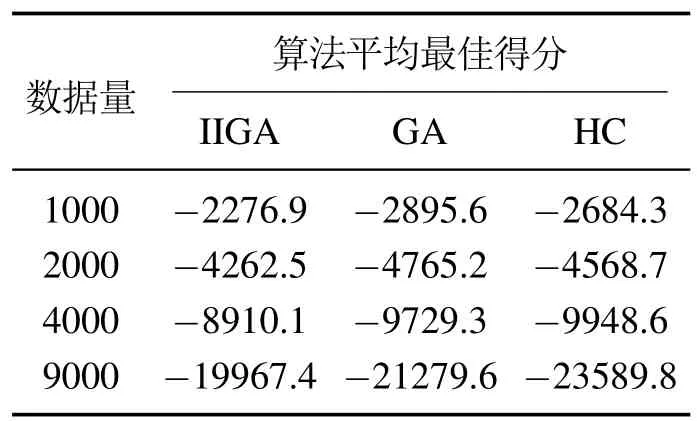
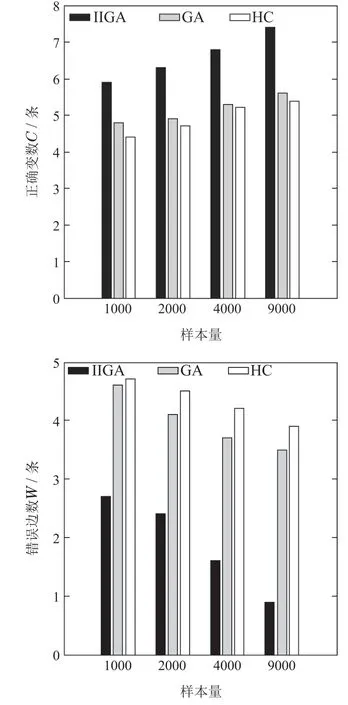
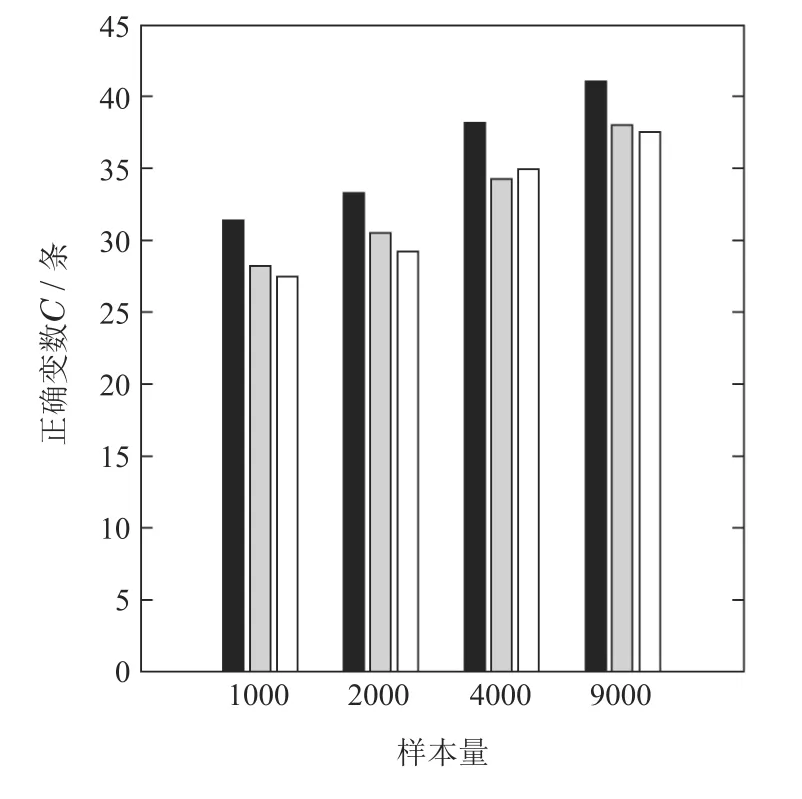
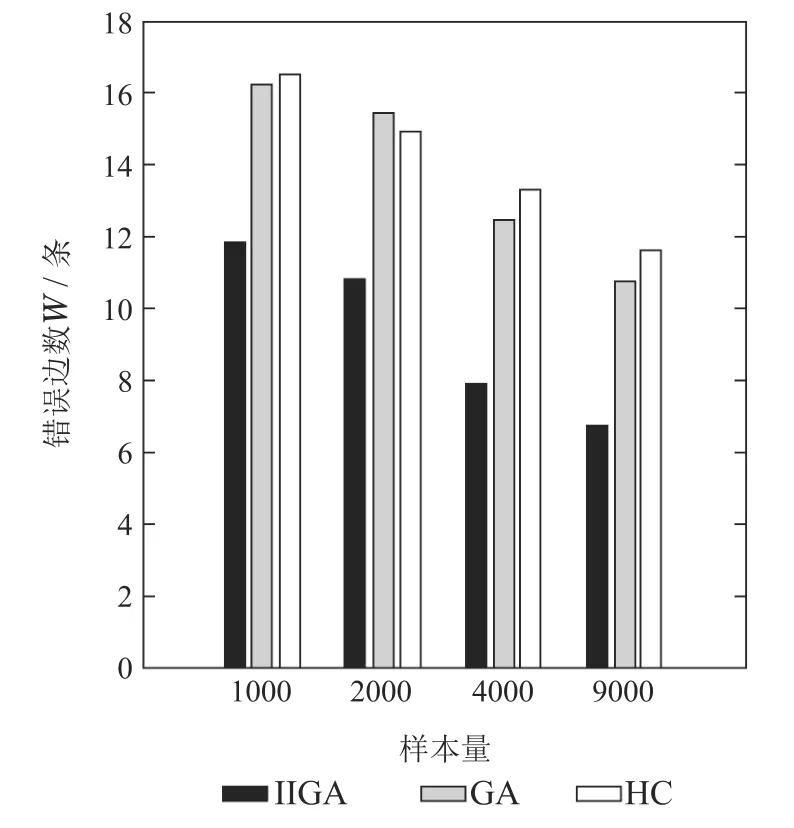
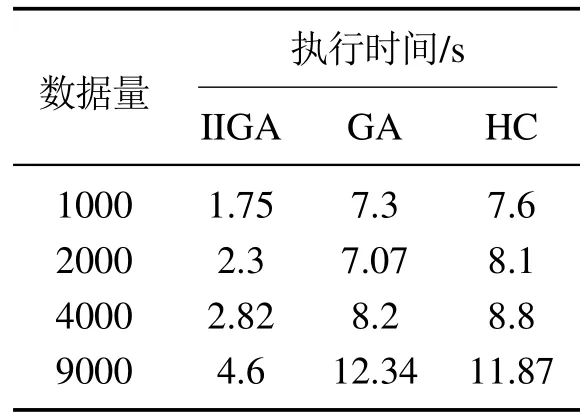
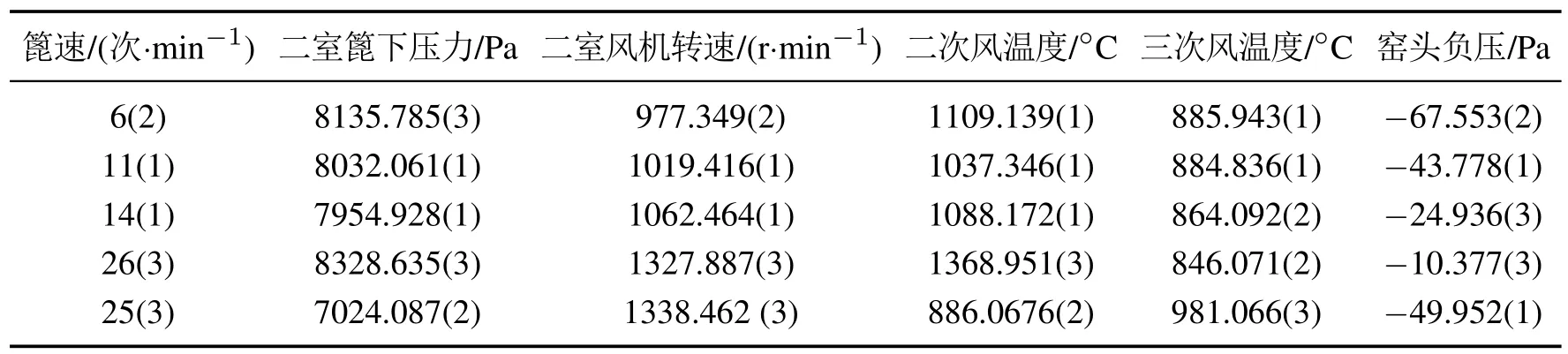
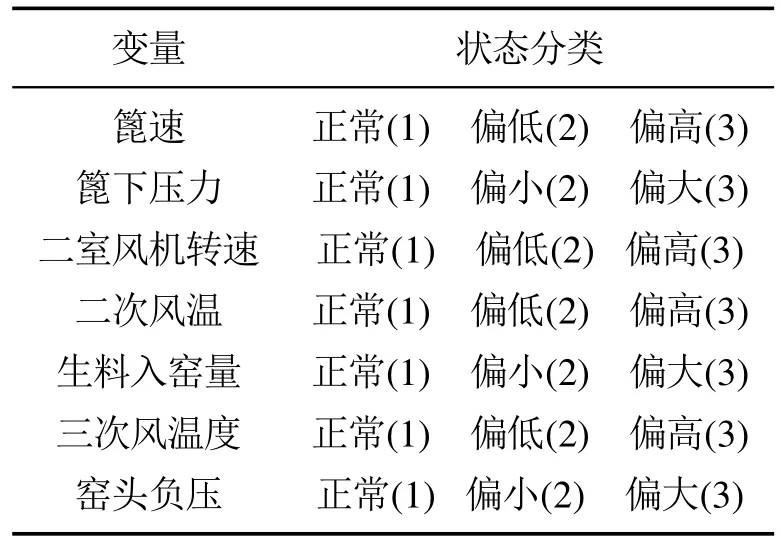
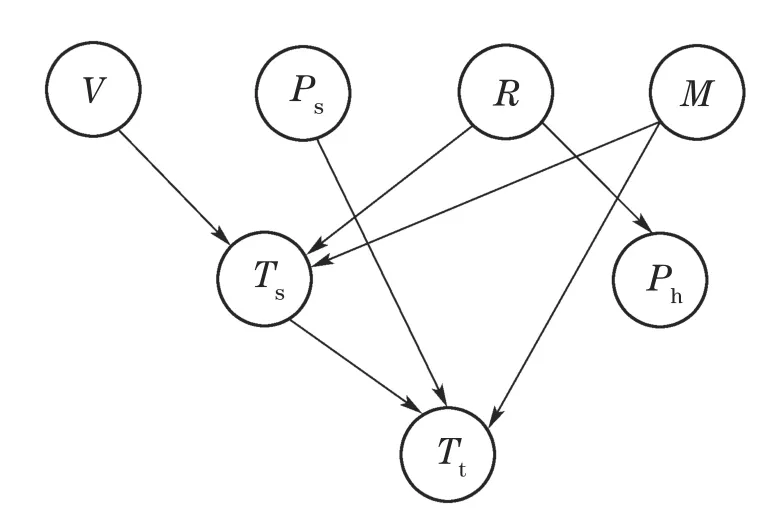
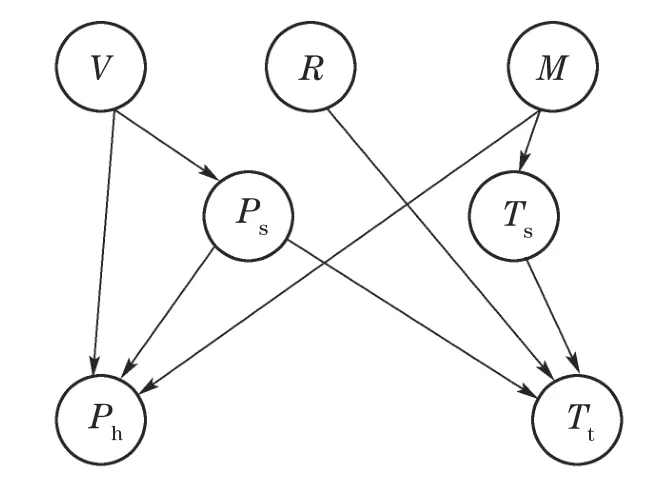
7)判断Nc IIGA算法流程如图6所示. 仿真实验的操作系统为Windows 7,CPU为i3–3240内存为4 G,软件环境为MATLAB R2010a.基于贝叶斯网络工具箱FullBNT–1.0.7[17]中的Asia网络、Car网络、Alarm网络进行仿真实验.其中标准的Asia网络具有8个节点、8 条边;标准的Car网络具有12个节点、9条边;标准的Alarm网络具有37个节点、46条边. 根据IIGA算法收敛性分析可知:算法经过有限次迭代后一定有存在最佳区域的个体,其中最大迭代次数是通过实验确定的.为保证算法搜索到的结构为最优的,先将实验中的迭代次数规定为搜索到与标准网络得分相同时对应的次数,然后在Asia网络、Car网络、Alarm网络随机生成数据量为1000,3000,4000,5000,9000的数据样本.每种样本容量分别产生10个,且每个数据单独运行10次,即每组数据运行100 次后取平均值作为最终实验结果,图7为不同的数据量下的平均迭代次数. 图6 IIGA算法流程Fig.6 Flow chart of IIGA 图7 平均迭代次数Fig.7 The number of average iteration 由图7可知,在不同的网络中算法收敛的迭代次数是不同的,在Asia网络中迭代次数在20∼27左右,在Car网络中迭代次数在25∼32左右,在Alarm网络中迭代次数在35∼45左右,为保证所有的数据量下算法收敛,将不同的数据中迭代次数的平均值加上其标准差作为最大迭代次数.因而设置Asia网络的最大迭代次数为30,Car网络的最大迭代次数为38,Alarm网络的最大迭代次数为56. 将IIGA算法与GA算法,爬山算法(hill climbing,HC)进行实验对比.其中IIGA算法的初始种群为42,设定依据为种群规模越大越可能找到全局最优解,但运行时间也相对较长,在小中规模变量的节点下,一般在40∼100之间取值,本文在Asia网络、Car网络、Alarm网络进行多组多次预实验,在Asia网络和Car网络中,种群规模大于等于30和38时搜索到全局最优结构,在Alarm网络中,种群规模等于42和大于42时搜索到算法评分函数最大的较优结构相同,因此IIGA算法统一选择42作为初始种群规模,参数σ,µ,rl是根据种群个体自适应产生.根据文献[8]将遗传算法的参数设置如下:初始种群为100,交叉概率为0.7,变异概率为0.3,最大迭代次数与IIGA算法相同.根据文献[6]可知HC 算法是从一个初始模型出发,利用加边、转边、减边3种算子随机搜索,搜索过程无参数.由于Asia网络、Car网络都是节点较少的网络,其实验结果有相似性,因而根据Asia网络与Alarm网络的实验结果分析算法.实验结果如下所示. 表1–2是不同算法在不同网络的平均BIC值. 表1 Asia网络不同算法平均最佳得分Table 1 Average best score of different algorithms in Asia network 表2 Alarm网络不同算法平均最佳得分Table 2 Average best score of different algorithms in Alarm network 由表1–2可知,在Asia网络和Alarm网络中利用IIGA算法进行结构训练得到的平均BIC值要高于GA算法和HC算法,这是由于IIGA算法中引入的改进免疫算子与自动交叉策略在一定程度上提升了GA算法与HC算法的全局寻优能力. 图8–9是不同算法在不同网络的结构对比,其中正确边数C为与标准结构相同的边,错误边数W为冗余边、丢失边、反转边之和. 图8 Asia网络边数对比Fig.8 The comparison of Asia edges 图9 Alarm网络边数对比Fig.9 The comparison of Alarm edges 由图8–9可知:在Asia网络和Alarm网络中,即使测试数据量较少,利用IIGA算法得到的准确边数也高于GA算法、HC算法.且随着数据量的增加,利用IIGA得到的准确边数在3 种算法中最多,错误边数均少于GA算法、HC算法.这是由于IIGA算法中引入的师生交流机制提高了算法的全局搜索能力,避免了算法陷入局部最优. 表3–4是不同算法在不同网络的时间对比. 表3 Asia网络不同算法的执行时间Table 3 Execution time of different algorithms in Asia network 表4 Alarm网络不同算法的执行时间Table 4 Execution time of different algorithms in Alarm network 由表3–4可知,在Asia网络和Alarm网络中利用IIGA算法进行结构的训练时间要远少于GA算法与HC算法,这是最大支撑数缩小了搜索的范围,且IIGA算法利用改进联姻策略提升算法的局部寻优能力,提高了算法的搜索效率. 水泥篦冷机的主要任务是对回转窑窑头卸下的高温熟料进行冷却,同时将热交换得到的热量引入回转窑与分解炉进行回收利用,从而达到熟料冷却与热量回收的目的[19].篦冷机的故障是篦冷机相关控制部件和调节器出现损坏和设置不合理,导致水泥生产中的冷却和热量回收受到一定程度的影响,表现为在相关节点测量的数据处于非正常范围.由于篦冷机系统的工艺参数多且关系错综复杂等因素导致对篦冷机建模比较困难,目前国内篦冷机的故障诊断大多采用人工排查的方式[20].而贝叶斯网络具有强大的推理能力和方便的决策机制,因而可利用贝叶斯网络对篦冷机进行故障诊断.故障诊断根据不合理数据所处的情况(节点的状态),运用贝叶斯故障诊断,进行因果分析,诊断故障原因.篦冷机二次风温的故障诊断模型包括结构学习、参数学习以及诊断推理,其中结构学习是参数学习与诊断推理基础.模型的构建过程是首先根据水泥篦冷机的运行原理,确定贝叶斯网络的节点变量.然后对IIGA算法构建的结构进行参数学习和诊断推理,最终得到水泥篦冷机二次风温的故障诊断模型. 篦冷机主要部件包括上壳体、下壳体、篦床、冷却风机、液压传动系统、熟料破碎机等,结构简图如图10所示. 图10 篦冷机结构简图Fig.10 Structural sketch of cement grate cooler 根据文献[18]选择了7个相关程度较高的篦冷机工艺参数:篦速(V)、二室篦下压力(Ps)、二室风机转速(R)、二次风温度(Ts)、生料入窑量(M)、三次风温度(Tt)和窑头负压(Ph),利用IIGA算法对量化的数据进行训练得到篦冷机故障诊断结构.其中二次风温等工艺参数采集的现场数据及对应量化处理值如表5所示(由于篇幅限制,仅列举5 组),对应状态如表6所示,其中表5–6括号中的数字1,2,3是实际数据量化的变量,实际含义为:1表示测量值处于正常范围内;2表示测量值低于正常范围;3表示测量值高于正常范围.以1000组数据为例,利用IIGA算法训练得到的故障诊断结构如图11所示,利用HC,GA训练得到的结构分别如图12–13所示. 表5 部分数据样本及量化举例Table 5 Data samples and quantification 表6 变量状态分类Table 6 States of variables 图11 利用IIGA算法得到的诊断结构Fig.11 Diagnosis structure obtained by IIGA 图12 利用HC算法得到的诊断结构Fig.12 Diagnosis structure obtained by HC 图13 利用GA算法得到的诊断结构Fig.13 Diagnosis structure obtained by GA 综合图11–13可知:利用HC,GA得到的诊断结构偏差较大,如:利用HC算法得到的结构忽略了喂料量对二次风温的影响,错误添加了二室风温对二室篦下压力的影响.利用GA算法得到的诊断结构忽略了二室风机转速以及篦速对二次风温的影响,错误添加了喂料量对窑头负压的影响. 上节分别利用IIGA,GA,HC算法构建了篦冷机工艺参数的故障诊断模型,然后需要对模型进行参数学习与故障诊断推理.常用的参数学习方法有最大似然估计法(maximum likelihood estimation,MLE)和贝叶斯估计法(Bayesian estimation)[17],本文直接利用MLE法对模型进行参数学习.然后利用变量消元法[19]进行故障诊断,通过计算原因节点的后验概率来查找导致故障的原因. 二次风温与三次风温是衡量热回收效率的重要工艺参数[20],其中二次风温一般保持在980◦C∼1200◦C,三次风温一般保持在880◦C∼980◦C.二者的参数学习与推理过程是类似的,并且由IIGA算法构造的诊断模型结构可知,二次风温是三次风温的父节点,即二次风温的状态变化会影响三次风温的状态,若二次风温偏高,会直接导致三次风温偏高;若二次风温偏低,同样会导致三次风温偏低.因而以二次风温为例详细说明诊断模型的参数学习与推理情况.以图11为例,节点V,R对应的条件概率如表7所示,节点Ph对应的条件概率表如表8所示,其中表7的篦速V、风机转速R是图11结构的两个根节点,表8的窑头负压Ph是图11结构的非根节点,所有节点(包括根节点和非根节点)的概率都是在结构和样本数据的基础上,进行参数学习,得到的参数表,也称概率表.表7篦速V、风机转速R的先验概率表和表8窑头负压Ph的条件概率表是在通过IIGA得到的篦冷机贝叶斯结构和数据样本基础上,进行参数学习(本文使用最大似然估计法)得到的. 二次风温在窑头负压作用下进入回转窑进行助燃,但二次风温偏低会使热回收效率变差,造成燃料煤的大量浪费,同时产生了大量废气污染环境,适当提高二次风温可节省燃煤,达到节约能源保护环境的目的;但二次风温偏高会造成熟料出篦的温度偏高,使篦冷机对水泥熟料的冷却效果变差.所以,本文利用IIGA算法对二次风温进行故障诊断. 如:监测到二次风温忽然偏低,由图11可知导致二次风温忽然偏低的原因有3个:篦速V,二室风机转速R以及生料入窑量M,以1000组数据为例,利用变量消元法计算V,R和M的后验概率,计算式如下: 通过比较后验概率α可知,二次风温度忽然降低是由于二室风机转速偏高导致的,及时减小风机转速,提升二次风温度,从而最大程度上减少燃煤的浪费与氮氧化物等污染废气的排放.同理,分别利用HC,GA以及IIGA算法对篦冷机熟料换热二次风温度进行故障诊断,所得诊断结果统计表如表9所示(由于篇幅有限仅列举5组). 通过诊断结果可得到各算法在每一组测试集的正确诊断故障数,然后根据式(23)可以得到3种算法的准确率对比.在相同的数据量下,为避免偶然性因素的影响,最后的实验结果是50次的平均值,图14为不同的数据下不同算法正确诊断率的对比. 式中: H为正确诊断率;|Dtrue|为诊断正确的数据数;|Dtest|为测试集大小. 由图14可知,在每组测试数据中,利用IIGA对二次风温进行故障诊断的准确率要高于HC算法和GA算法,在数据量为1000的时候,IIGA算法分别比HC算法和GA算法高8%和5%,且准确率随着数据量的增加而增加.基本满足实际生产中二次风温故障诊断的需求. 表9 各算法诊断结果对比Table 9 Diagnosis results comparison of each algorithm 图14 各算法诊断准确率对比Fig.14 Diagnosis accuracy of each algorithm 本文提出的IIGA算法利用最大支撑树与评分函数建立两个初始种群,提升算法的收敛速度;引入自适应免疫算子,自动交叉变异算子与师生交流机制改善了遗传算法的全局寻优能力;利用改进联姻策略提升了算法局部寻优能力.实验结果证明,利用IIGA算法进行结构训练,所得模型的准确度要高于GA,HC算法,运行时间缩短.利用IIGA算法建立了水泥熟料换热的工艺参数故障诊断模型,对二次风温度实现了较为准确的故障诊断,避免了由于二次风温故障诊断不及时导致浪费煤等能源、产生大量污染废气等问题.同时也为篦冷机熟料换热工艺参数建模以及故障诊断提供了一种新的思路.但在数据量较大时,故障诊断的效率有所下降,因而下一步计划是增量学习,即先在较少的数据量下学习到一个结构,然后在此基础上增加数据并更新结构,保证最终学习到的结构更加匹配数据.3 IIGA算法仿真实验

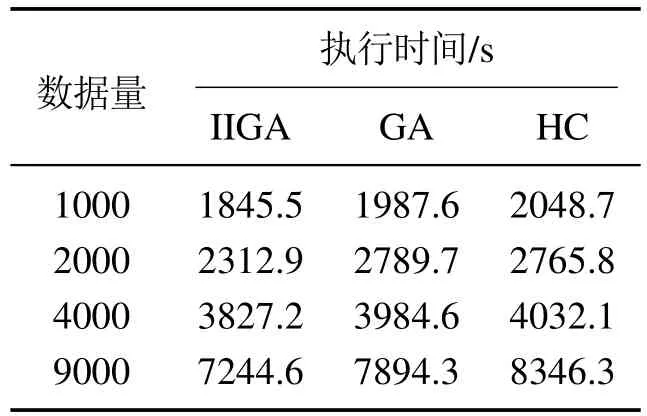
4 篦冷机水泥熟料换热二次风温故障诊断
4.1 变量选取与工艺参数建模


4.2 参数学习与熟料换热二次风温故障诊断




5 结论
