基于改进狼群算法的模糊时间序列预测模型
2020-08-14鲜思东李堂金
鲜思东 ,李堂金
(1.重庆邮电大学复杂系统智能分析与决策重点实验室,重庆 400065;2.重庆邮电大学自动化学院,重庆 400065)
1 引言
以时间轴为依据,按照一定的时间间隔记录的数据称为时间序列.利用时间序列进行分析是预测未来结果最古老和最可靠的技术之一.传统的时间序列预测方法不能解决时间序列值为“差”、“中等”、“好”等由语言术语描述的问题.为了克服这一缺陷,Zadeh教授提出了模糊集(fuzzy sets,FS)理论[1],Song和Chissom将模糊集理论成功引入时间序列模型中,首次提出了模糊时间序列(fuzzy time series,FTS)模型[2–4].在这种模型中,观测值是模糊集,并在当前状态和以前状态之间建立关系.
模糊时间序列的另一个特点是它分析处理小数据集的能力相对于传统的时间序列更好.20多年以来,广大学者们在大学招生[2,5–14]、气候学[8–9,15]、股票市场[5,8–10,16–19]、医疗健康[20]、旅游[21]等不同的应用领域建立了许多模糊时间序列预测模型.
论域划分是影响模糊时间序列模型预测精度的关键因素之一[5].论域划分方法可以分为两类:等长度划分和非等长度划分.早期的研究都采用相等长度的论域划分方法[6–7],现在学者们更多地采用了非等长度的论域划分方法.在基于数学模型的划分方法中,“最小熵原理法”和“梯形模糊化法”[22]、自动聚类技术[8,16]、“动态挖掘距离法”[23]、“基于均值的离散化法”[9]都表现出了较好的性能.此外,为了提高预测精度,“信息粒”[10,17]和“模糊离散化技术”[24]也被用来划分区间.在基于仿生优化算法的论域划分方法中,粒子群优化算法(particle swarm optimization,PSO)[11–12,25]、蚁群优化(ant colony optimization,ACO)[18]、遗传算法(genetic algorithm,GA)[13,19]、人工鱼群算法(artificial fish swarm algorithm,AFSA)[14,26]均取得了不错的效果.
为了进一步提高模糊时间序列预测模型的预测精度,本文将狼群算法(wolf pack algorithm,WPA)进行了改进并用于模糊区间的划分,提出了一种基于改进的狼群算法(improved wolf pack algorithm,IWPA)的模糊时间序列预测模型(IWPA–FTS).首先针对基本狼群算法在游走过程中收敛速度慢、容易陷入局部极值的缺陷,引入趋向行为和死亡概率,有效提高探狼的收敛速度和跳出局部极值的能力.然后将改进的狼群算法用于优化论域的划分.最后以Alabama大学入学人数作为实验数据来验证所提模型的有效性.通过与现有的一些模型进行对比分析,本文所提模型具有更高的预测精度.
2 模糊时间序列(FTS)
定义1设X为论域,X由有限个离散的元素构成,即X{x1,x2,···,xn}.则定义在论域上的模糊集合可以表示为
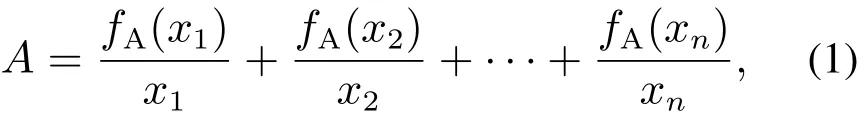
其中:fA是模糊集合A的隶属度函数,并且fA:X →[0,1],fA(xi)表示xi属于模糊集A的隶属度值.
定义2设论域Y(t)(t···,0,1,2,···)是实数集R上的一个子集,fi(t)(i1,2,···)是定义在Y(t)上的模糊集.如果F(t)是f1(t),f2(t),f3(t),···的一个集合,即F(t){f1(t),f2(t),f3(t),···},则把F(t)称为定义在Y(t)上的模糊时间序列.
定义3设F(t)(t1,2,3,···)为一个模糊时间序列,如果F(t)由F(t−1)确定,R(t −1,t)为F(t)和F(t −1)之间的模糊逻辑关系(fuzzy logic relation,FLR),则
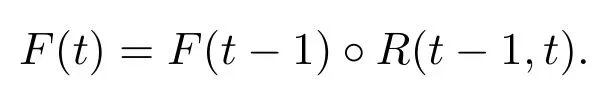
定义4设有一组一阶模糊模糊逻辑关系为Ai→Ak1,Ai→Ak2,···,Ai→Akm,即它们拥有相同的当前状态,则可以用一个模糊逻辑关系组(fuzzy logical relation group,FLRG)将它们表示为
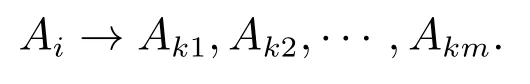
定义5设F(t)由F(t −n),F(t −n+1),···,F(t −1)导致,则n阶模糊逻辑关系可以表示为
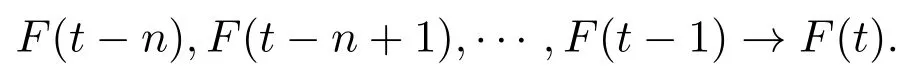
模糊时间序列的一般预测步骤如下:1)确定并划分论域;2)模糊化实际数据;3)建立FLRs和FLRGs;4)去模糊化计算预测值.
3 改进的狼群算法(IWPA)
吴虎胜等人受到自然界狼群狩猎行为和它们的猎物分配模式的启发,提出了狼群算法(WPA)[27],并用它来解决优化问题.WPA中的狼一般分为3类:头狼、探狼和猛狼,狼群的整个捕食行为被抽象为3种智能行为,即游走、召唤和围攻行为,以及两种智能规则,即“胜者为王”的头狼生成规则和“强者生存”的狼群更新规则.下面对这些行为和规则进行详细的说明.
假设人工狼群的猎场空间为N ×D维,其中N为人工狼的数量,D为解空间变量的个数,则第i匹人工狼的位置可以表示为
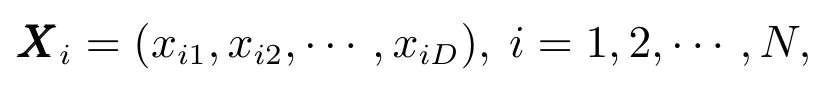
xid(d1,2,···,D)为人工狼i的第d个待寻优的变量.位置在XXXi的第i匹人工狼的适应度值(目标函数值)可定义为Yif(XXXi).
1)“胜者为王”的头狼产生规则:在初始解空间中,选择目标函数值最优的人工狼为头狼.每次迭代后,将目标函数值最好的人工狼与上一代头狼进行比较.如果它的目标函数值更好,那么上一代头狼将被替换,头狼的位置将被更新.头狼不参与执行3种智能行为,而是直接进入下一次迭代,直到被更强的狼替换.
2)游走行为:除了头狼外,让目标函数值最佳的Snum匹人工狼充当探狼.Snum是在区间中随机选择的整数.α为探狼比例因子.首先,探狼分别向h不同方向迈出一步,记录每个方向的适应度值.然后回到原来的位置.探狼i向第p(p1,2,···,h)个方向迈出一步后,它的位置表示为

其中:rand()是在区间[−1,1]中均匀分布的随机数,stepa表示游走步长.探狼i向h个方向中选择具有最优适应度值且优于原位置的方向前进一步,更新位置XXXi.重复上述行为直到某匹人工狼的适应度值优于头狼或者达到最大游走次数Tmax.
3)召唤行为:头狼通过嚎叫召唤周围的Mnum匹猛狼快速向头狼靠近.其中MnumN −Snum−1.猛狼以相对较大的步长stepb向头狼的位置聚集.猛狼i的位置更新式如下:

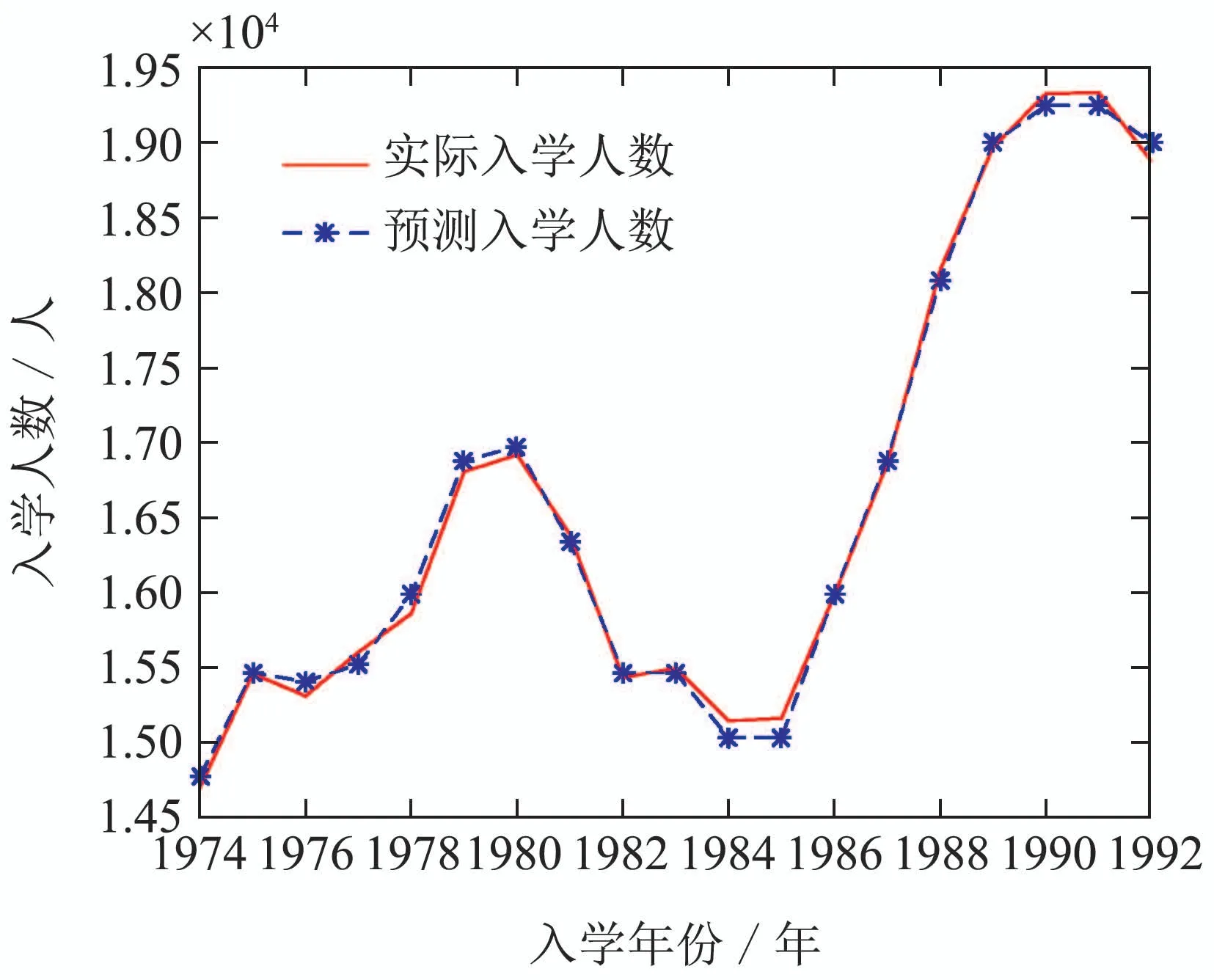
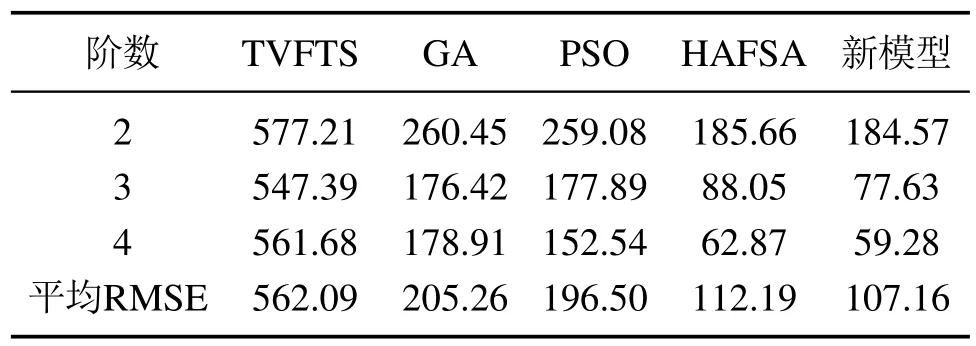
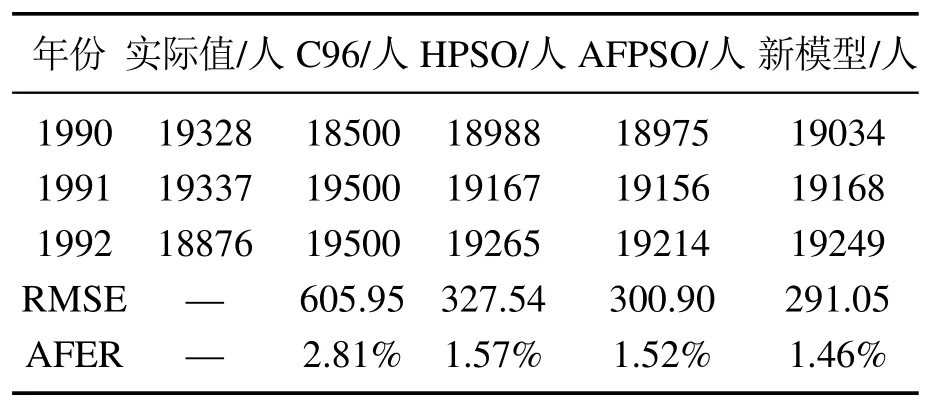
其中GGGk是第k代头狼的位置.在奔袭的过程中,如果猛狼i的适应度值Yi比头狼的适应度值Ylead更好,该猛狼将代替头狼,同时YleadYi.然后由新的头狼发起召唤行为.否则,猛狼i继续向头狼的位置靠拢直到d(i,lead) 其中:ϖ是距离判定因子,[mind,maxd]是第d个变量的取值范围. 4)围攻行为:通过向头狼的位置聚集后,猛狼离头狼的位置都比较近了.这时将头狼的位置视为猎物的位置,猛狼将和探狼一起进行围攻猎物.围攻过程中人工狼i的位置更新式如下: 其中: λ是在区间[−1,1]均匀分布的随机数;stepc表示围攻步长.如果人工狼i执行围攻行为后,新位置的适应度值优于原位置的值,则更新该狼的位置XXXi.否则不变. 在3种智能行为中涉及的步长stepa,stepb和stepc之间具有如下的关系: 其中S表示步长因子,它决定了人工狼在解空间寻找最优解的精细程度. 5)“强者生存”的狼群更新规则:这个规则模拟达尔文提出的自然选择法则.为了保障种族的延续,食物按照先强后弱的顺序进行分配,这会导致一些弱小的狼因为分配不到食物而饿死.在实际算法中表现为淘汰m匹具有最差适应度值的人工狼,同时在解空间内随机生成m匹新的人工狼.m是在区间随机选择的一个整数.β为群体更新比例因子. WPA算法具有良好的全局收敛能力,同时也有一些缺点,如收敛速度慢、容易陷入局部极值等.本文对WPA的游走行为进行改进,提出了改进的狼群算法(IWPA). 在狼群算法的游走行为中,当h个方向中具有最优适应度值的位置比原位置好的时候,人工狼仅仅向该方向前进一步,然后重新选择h个方向重复前面的行为,这导致了狼群算法的收敛速度过慢.事实上,具有最优适应度值的方向是最可能改善适应度值的方向.因此,为了加速狼群算法的收敛速度,本文在这里引入一个趋向行为.当人工狼朝着改善适应度值的方向移动一步后,人工狼将继续沿同一方向前进几步,直到人工狼的适应度值不再改善或移动步数(Ns)达到了最大值(Nsmax).在前进的过程中,人工狼的位置更新式如下: 其中:rand是在区间[0,1]之间均匀分布的随机数, 为适应度改善的方向,XXXj为具有更优适应度值的位置向量. 另外,在游走过程中,当h方向中的最优适应度比初始位置差时,算法可能已经陷入局部极值.在这种情况下,为了提高人工狼跳出局部极值的能力,本文做出如下改进:对于上述情况的人工狼,本文设置一个死亡概率Pe,当人工狼满足死亡概率时,该人工狼死亡,并随机地在解空间的任何地方生成一个新的个体,否则位置不变.改进后的人工狼游走行为的伪代码如算法1所示. 算法1改进后的游走行为. 为了进一步提高模糊时间序列模型的预测精度,本文将IWPA算法用于模糊区间的划分,建立了IWPA–FTS预测模型.利用IWPA寻找最优的区间划分点的具体步骤如下: 步骤1初始化参数. 步骤2计算每匹人工狼在当前位置的适应度值. 步骤2.1模糊化每一个历史数据. 在模糊时间序列中,模糊集通常由下面的公式定义: 其中u1,u2,u3,···,un表示区间. 确定好模糊集后,就可以将每个数据模糊化.为了确定数据x所对应的模糊集,本文首先要确定数据x所属的模糊区间ui,然后计算数据x属于区间ui的隶属度值,接着找出最大隶属度值所对应的模糊集Ai.最后,数据x就被模糊化为Ai. 步骤2.2建立模糊关系和模糊关系组. 通过定义3–4建立FLRs和FLRGs.高阶FLRs可根据定义5建立. 步骤2.3去模糊化并计算预测值. 预测值通过两种不同的方法计算:对训练阶段的数据采用基于下一状态嵌入式贝叶斯网络(embedded Bayesian network,EBN)的方法,对测试阶段的数据采用主投票(master voting,MV)方法进行计算. Kuo等[28]提出了EBN算法.其基本思想是:对每一个FLRG中的所有下一状态所对应的模糊区间等长度划分为3个小区间,然后根据下面的表达式计算出预测值: 其中: n表示在同一FLRG中下一状态的总数,midk(1kn)表示下一状态对应的模糊区间的中点值,submidk表示第k个下一状态所对应的实际数据在3个小区间中所属的那个小区间的中点值.为便于理解,本文举个简单的例子进行说明:假设在某一FLRG中的其中一个下一状态对应的实际数据为1550并且该状态对应的模糊区间为ui[1000,1600],则这3个小区间分别为ui1[1000,1200],ui2(1200,1400],ui3(1400,1600].因此, 在测试阶段,本文采用Kuo等[11]提出的MV方法.其计算式如下: 其中λ代表预测时需要用的与预测时刻相邻的前面时刻数据的个数,mti(i1,2,···,λ)为前面第i时刻的数据所属模糊区间的中点值,Wh表示与预测时刻相邻时刻的数据对预测值的影响程度.为了方便比较,本文取Wh15. 步骤2.4计算适应度值. 本文把预测值与真实值之间的均方根误差(root mean square error,RMSE)作为人工狼的适应度值,其计算式如下: 比较所有人工狼的初试适应度值,选取拥有最优适应度值(最小RMSE值)的人工狼作为头狼. 步骤3选择人工狼的行为. 步骤3.1除头狼外,选择Snum匹具有最佳适应度值的狼作为探狼,执行改进的游走行为,直到某匹狼的适应度值优于头狼或者达到最大游走次数Tmax,然后转向步骤3.2. 步骤3.2头狼通过嚎叫执行召唤行为.剩余的Mnum匹猛狼快速向猎物靠近.在奔袭的过程中,如果某匹猛狼的适应度值优于头狼,则该猛狼将代替头狼并发起召唤行为,否则,猛狼继续向头狼靠拢直到与头狼的距离d(i,lead) 步骤3.3探狼和猛狼一起执行围攻行为. 步骤3.4根据“强者生存”的狼群更新原则更新狼群. 步骤4判断结束条件. 如果算法达到最大迭代次数M或者已经达到预设精度,则输出最后一次迭代后头狼的适应度值和相应的位置向量,同时得到的还有模糊时间序列、FLRs、FLRGs和训练阶段的预测值.否则,重复步骤3–4. 在本节中,利用了Alabama大学1971年至1992年的实际入学人数(表1第2列)来证明本文所提模型的有效性.本实验使用MATLAB 2016a编写仿真程序,在Windows 10操作系统,因特尔i5–6500 3.19 GHz处理器,16 G内存的PC机上实现.预测精度通过式(11)定义的均方根误差(RMSE)和式(12)平均预测误差率(average forecasting error rate,AFER)进行测量,AFER定义如下: 相对应的模糊化结果、3阶FLR以及训练阶段的预测值都如表1所示.图1为训练阶段的实际入学人数与预测入学人数的对比.从图1中可以清楚地看出,运用本文的模型计算出的预测值与实际值非常接近. 表1 实际数据和训练阶段结果Table 1 Actual data and training phase results 为了直观地说明IWAP的优越性,本文对混合人工鱼群算法(hybrid artificial fish swarm algorithm,HAFSA)[26]、WPA和IWPA3种算法划分论域进行了比较,这里区间划分个数为7,模型阶数为2,仿真结果取20次运行结果的平均值,它们的收敛曲线如图2所示,优化结果及耗时情况如表2所示.由图2可知,IWPA具有更快的收敛速度和更高的优化精度.在表2中,根据最好的最优值、最差的最优值、平均最优值3项指标可以看出,IWPA获得的结果最好,其次为WPA和HAFSA.另外,根据平均耗时情况来看,虽然WPA的耗时比HAFSA多,但是WPA的优化精度要比HAFSA高.IWPA耗时最少获得的精度最高.说明本文在WPA算法的游走行为中引入的趋向行为和死亡概率能有效改善WPA算法的收敛速度和优化精度. 图1 实际值与预测值对比结果Fig.1 Actual vs forecasted 图2 3种算法仿真结果比较Fig.2 Comparison results of three different algorithms 表2 优化结果比较Table 2 The comparison of optimization results 为了验证IWPA–FTS模型预测精度的提高,本文选取C96[6],Q11[29],W13[30],PSO[25],IFTS[31]以及HAFSA[26]多种预测模型进行比较,所有模型的区间划分数都取7.比较结果如图3所示,从图3可以明显看出本文所提模型在训练阶段的预测精度最高. 为了验证本文所提模型在不同阶数情况下预测精度的有效性,本文与4个现有的预测模型:TVFTS[32],GA[33],PSO[11],HAFSA[26]分别在2阶、3阶和4阶的情况下做了一个对比.所有预测模型的区间划分个数为7,对比结果如表3所示.可以看出本文的模型在不同阶情况下均得到了最小的RMSE值以及最小的平均RMSE值. 图3 不同模型预测精度比较Fig.3 Comparison results of various forecast models 表3 不同阶数情况下的对比结果Table 3 Comparison results of different orders 为了验证本文所提模型在测试阶段的效果,即预测未来的能力.本文将实际数据的最后3个作为测试数据集,根据剩余的19个数据建立相应的FLR和FLRG,对最后3个数据进行预测.将本文的预测结果同模型C96[6],HPSO[11],AFPSO[12]的预测结果进行对比,所有模型都采用MV方法进行预测,Wh15,λ3,区间划分个数n7,模型阶数为3,比较结果如表4所示.从表4可以看出,本文所提模型得到的预测结果具有最小的RMSE值和AFER值. 表4 测试阶段预测结果比较Table 4 Comparison of the predicted results for the testing phase 本文提出了一种基于改进狼群算法的模糊时间序列预测模型,并用它来预测Alabama大学的入学人数.本文的主要创新点和贡献如下:首先,提出了改进的狼群算法(IWPA),有效地提高了算法在游走阶段的收敛速度和跳出局部极值的能力.其次,本文首次将模糊时间序列与狼群算法相结合提出了IWPA–FTS预测模型,拓宽了狼群算法的应用范围.最后,通过与各种预测模型相比,本文所提模型在训练阶段和测试阶段均能获得较好的预测性能,证实了该模型的有效性.
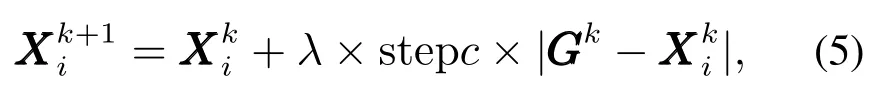
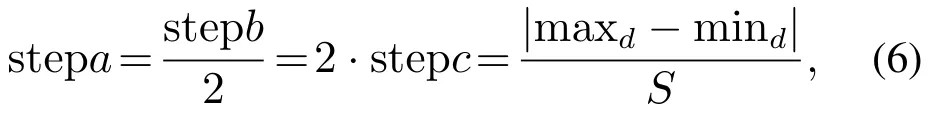




4 IWPA–FTS预测模型
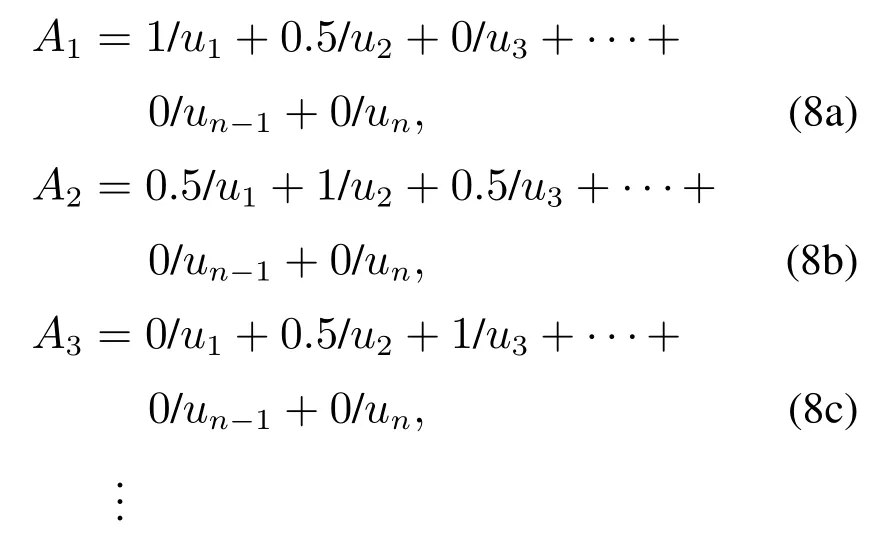
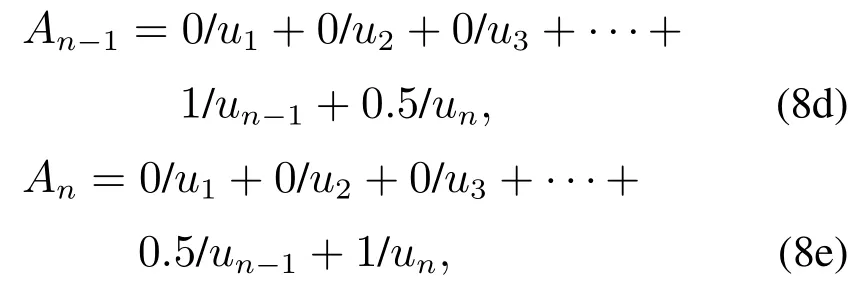

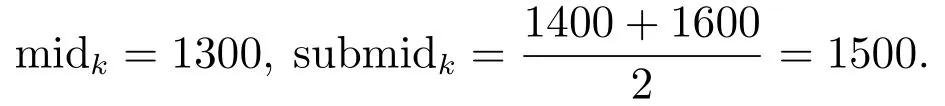
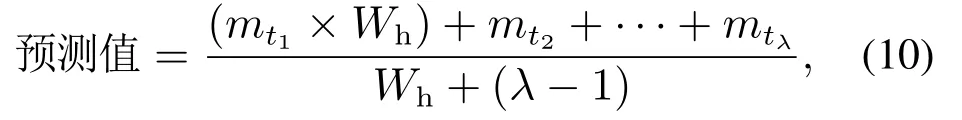

5 实例分析

5.1 训练阶段





5.2 测试阶段
6 结论
