基于Petri网诊断器的离散事件系统模式故障的在线诊断
2020-08-14阙蔡雄刘富春邓秀勤崔洪刚
阙蔡雄 刘富春 赵 锐 邓秀勤 崔洪刚
(1.广东工业大学计算机学院,广东广州 510006;2.广东工业大学应用数学学院,广东广州 510006;3.东源县科技创新中心,广东河源 517500)
1 引言
近年来,离散事件系统的故障诊断成为一个热门的研究领域,备受国内外专家学者的关注.Sampath等提出了一种故障诊断方法[1],是目前离散事件系统故障诊断研究中最为广泛使用的方法.在文献[1]中,离散事件系统被建模为一个有限状态自动机,其故障诊断的目的在于当系统发生故障之后,在一定的延迟之内将其检测出并加以隔离.文献[2]将故障诊断方法由集中式系统推广至分布系统,提出一种分布式离散事件系统的故障诊断方法.文献[3]提出了一种异步诊断方法,允许诊断器与系统不在同一时刻初始化.文献[4]针对随机离散事件系统提出了一种稳健诊断方法,它允许系统的实际模型是不确定模型.文献[5]提出了一种双模糊离散事件系统,并基于该框架研究了基于状态的分布式诊断问题.本文作者也对离散事件系统的故障诊断问题及与之密切相关的不透明性问题进行了相关研究,提出一种随机离散事件系统的安全诊断方法[6]和一种不完备系统当前状态不透明性的验证算法[7].
上述文献考虑的均为对单个故障事件的诊断,然而在许多应用中,例如网络入侵探测,需要诊断的往往是一连串事件(称为一个模式).Genc等[8]和Jeron等[9]提出了模式诊断的概念和相应算法.Genc等提出了两种模式故障类型:S型模式故障和T型模式故障,其中S型模式故障考虑的是在语言中以子序列的形式发生的故障,而T型模式故障考虑的是在语言中以子串的形式发生的故障.Jeron等提出了监督模式的概念,一个监督模式指的是一个自动机,其标记的语言是需要诊断的模式的集合.本文作者也对模式故障诊断进行了研究,考虑了基于模式的安全故障诊断问题[10]和模糊离散事件系统的模式故障诊断问题[11].
离散事件系统的故障诊断问题又可以分为离线诊断和在线诊断.关于在线诊断,文献[1]给出的在线诊断方法不需要储存整个诊断器而只需储存诊断器的当前状态,但具体算法没有给出.文献[2]提出了一种在多项式的时间内即可得出诊断结果的在线诊断算法.文献[12]提出一种针对随机离散事件系统在线诊断方法.文献[13]构造了一种Petri网诊断器对离散系统进行在线诊断,这种Petri网诊断器可在多项式时间内构造完成,而且可以方便地应用于可编程逻辑控制器(programmable logic controller,PLC).文献[14]研究了离散事件系统的主动诊断问题,研究了一种N–可诊断性.
值得指出的是,近年来以Petri网为诊断器模型的故障诊断方法也引起了国内外的重视.文献[15]提出一种基于Petri网的在线诊断算法,该算法使用基于g-标记的线性编程方法来对故障事件进行在线诊断,避免了预先的离线计算.文献[16]提出一种基于网展开的在线诊断算法,有效地控制了状态爆炸问题,但这种方法也导致其在线诊断过程需进行大量的计算.文献[17]研究了以部分可观Petri网为模型的离散事件系统的在线诊断问题,提出一种整合广义互斥约束和整数线性编程的在线故障诊断算法.Gougam等[18]研究了基于Petri 网模型的离散事件系统模式故障诊断问题.文献[19]将模式故障诊断推广到了随机Petri网模型.文献[20]研究了定时系统中的模式诊断问题.
据大家所知,目前尚无用于模式故障的基于Petri网诊断器的在线诊断方法.本文继续了作者在文献[10–11]的工作,提出了一种用于模式故障的基于Petri网诊断器的在线诊断方法.首先讨论了离散事件系统的模式故障在线诊断问题,提出了自动机GD来对离散事件系统进行在线诊断.然后在GD的基础上,提出了Petri网诊断器的构造算法及在线诊断算法.本文将故障在线诊断问题推广至模式故障,得益于Petri网的分布性质(distributed nature),有效的避免了文献[1]中出现的状态爆炸问题,亦避免了使用诸如文献[16]的网展开方法,减少了诊断过程中的计算.本文提出的Petri网诊断器具有多项式时间的空间复杂度,具有所需空间小、效率高等特点.
本文接下来分为4节:第2节将介绍离散事件系统和Petri网的一些相关知识;第3节研究模式故障的在线诊断问题,提出一种用于S型模式故障诊断和T型模式故障诊断的有限状态自动机GD;第4节提出基于Petri网诊断器的模式故障在线诊断的验证算法并给出复杂度分析;第5节总结本文工作.
2 自动机与Petri网
为方便起见,引入以下符号:∥ω∥表示事件串ω的长度,σ ∈ω表示σ至少在ω中出现了一次,ωf表示事件串的最后一个事件,s ∈Sω表示s为ω的子序列,记号τ ∈Tω表示τ为ω的子串.投影P :Σ∗→是指一个满足如下规则的映射:对于任意σ ∈Σ,如果σ ∈Σo,则P(σ)σ,否则P(σ)ε,且P(ωσ)P(ω)P(σ).
集合Ψ(Σθ){ω ∈L:∃σ ∈Σθ,ωfσ},即L中以Σθ中任一事件结尾的串的集合.集合

即L中包含集合Σθ中任一事件的串的集合.模式故障串组成的集合记为K,
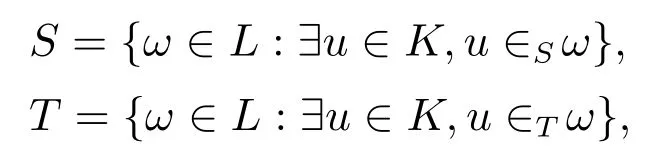
即S和T分别表示L中包含S型模式故障和T型模式故障的串的集合.集合

即ΨS(K)和ΨT(K)分别表示恰好发生S型模式故障和T 型模式故障的串的集合.
记号δ(x,σ)!表示转移δ(x,σ)在G中有定义.有效事件函数Γ :X →2Σ定义为Γ(x){σ :δ(x,σ)!}.对于任意x ∈X,

两个自动机G1和G2的并是一个自动机,其生成和标记的语言分别为
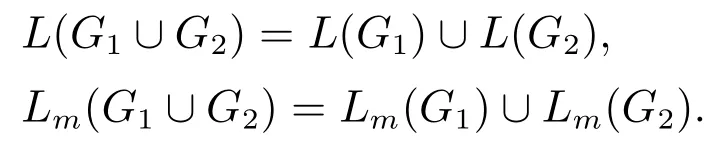
一个标签Petri网是一个七元组
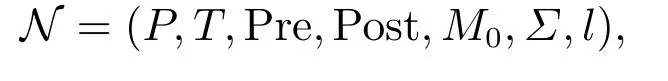
其中: P是库所的有限集,T是变迁的有限集,Pre(P×T)→{0,1,2,···}是连接库所和变迁的有向弧函数,Post:(T ×P)→{0,1,2,···}是连接变迁和库所的有向弧函数,M0:P →{0,1,2,···}是初始标识函数,l :T →2Σ为标签分配函数.库所pi含有的令牌数量表示为M(pi).标识

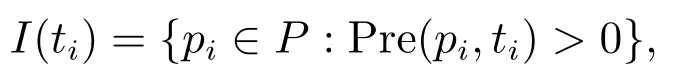
输出库所集为O(ti){pi∈P :Post(ti,pi)>0}.类似地,

3 模式故障的在线诊断
文献[8]给出了一种模式故障的离线诊断方法,在本节中作者将提出一种在线诊断方法,其主要思路如下:假设观察到的系统历史运行路径为ω(已发生的事件串),在每次观察到新事件σ发生后,计算出系统可能的实际运行路径∆{P−1(ωσ)∩L(G)}.若∆中所有的串都不包含故障,那么可以判定系统没有发生故障;若∆中既有包含故障的串,也有不包含故障的串,那么不能确定系统是否发生了故障;若∆中所有的串都包含故障,则可以判定系统发生了故障.用符号N表示系统没有发生故障,A表示不确定系统是否发生了故障,F表示确定系统发生了故障,则以上诊断过程可定义为函数diag.
定义1diag:→{N,A,F}为一个满足如下规则的函数:对于任意ωσ ∈
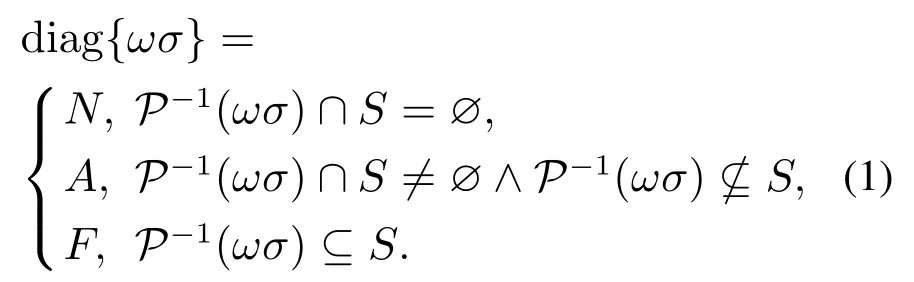
为方便起见,引入模式故障串标记自动机.
定义2给定一个模式故障串ki∈K及其模式故障类型,定义模式故障串标记自动机

其中: Xi{0,1,2,···,∥ki∥},
对于任意的x ∈Xi和σ ∈Σ,当ki为S型故障时,

当ki为T型故障时,

定义2中的Θ函数用来匹配当前已发生的串与模式串ki,其具体的算法可使用克努特–莫里斯–普拉特操作(Knuth-Morris-Pratt,KMP)算法.
定义3给定一个离散事件系统
和一个模式故障集K,令

则GD定义为

定理1给定一个离散事件系统G,一个模式故障集K及其模式故障类型,记L(G)L,

下面通过一个例子来说明如何根据GD和定理1对离散事件系统S型模式故障进行在线诊断,T型模式故障在线诊断方法可类似得到.
例1如图1所示,设系统G生成的语言为L,可观事件集为Σo{c,d,e},不可观事件集为Σuo{a,b},故障模式集为K{ac,bd},G关于L 是S 型模式故障可诊断的.根据定义2构造H(ac),H(bd)如图2–3所示,根据定义3构造G′,GD如图4–5所示.现在根据定理1用GD对系统进行在线诊断:假设历史运行路径ωcec,当观察到事件σd,可计算出δD(0,cecd){11,12},而{11,12}∩Xm,D{11}且{11,12}Xm,D,根据定理1,此时不能确定系统是否发生故障.同理,当继续观察到事件d后,计算出δD(0,cecdd){11},而{11}⊆Xm,D,根据定理1,可以确定系统发生了故障,诊断结束.其余路径的诊断过程相同.
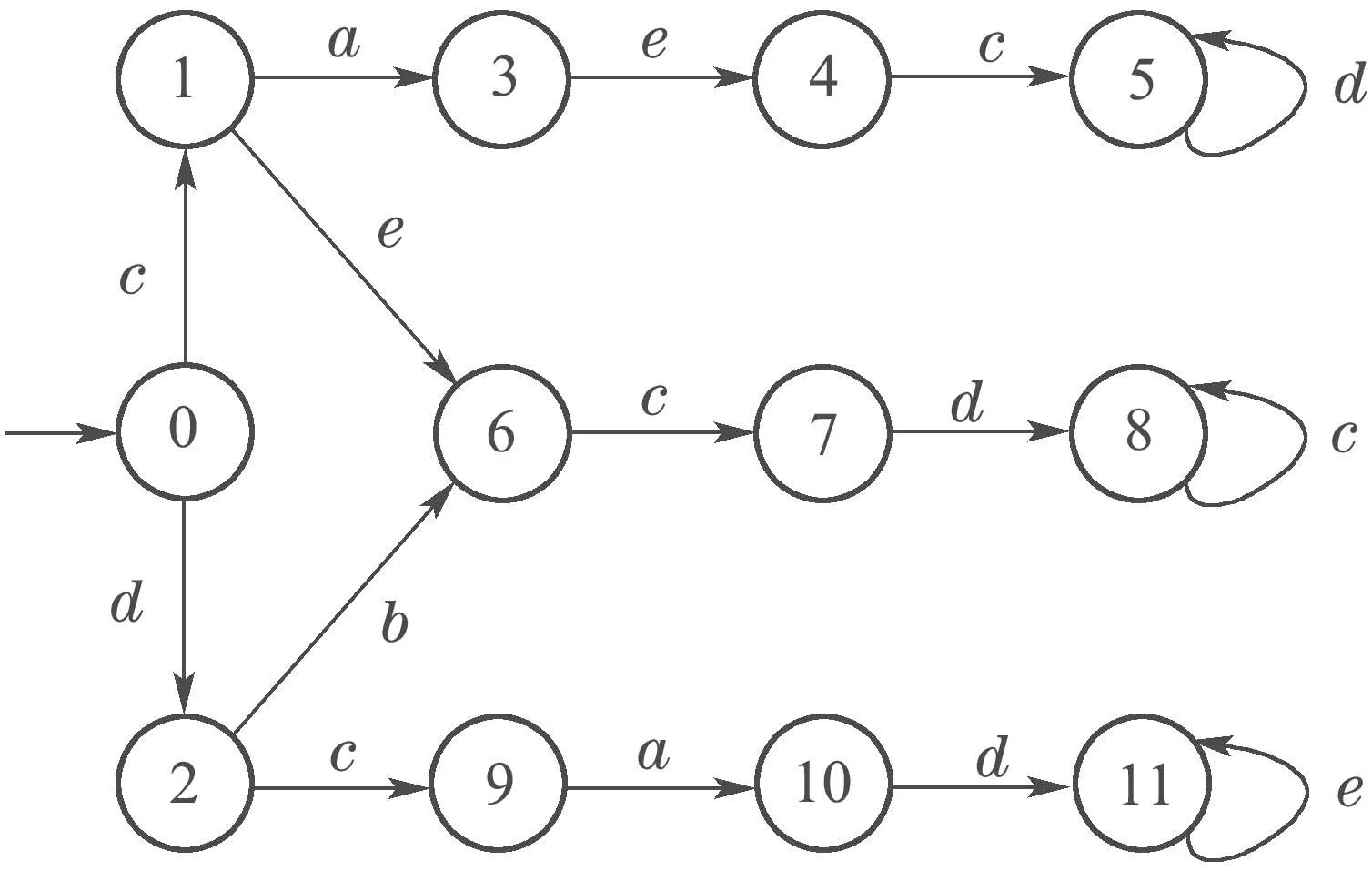
图1 一个离散事件系统GFig.1 A discrete-event system G

图2 自动机H(ac)Fig.2 Automation H(ac)

图3 自动机H(bd)Fig.3 Automation H(bd)

图4 自动机G′Fig.4 Automation G′
4 基于Petri 网诊断器的模式故障在线诊断的验证算法
为验证定理1中的条件,下面提出构建Petri网诊断器ND的方法(算法1)并给出基于Petri网诊断器的模式故障在线诊断的验证算法(算法2).
算法1构造Petri网诊断器ND.
输入:G,K.
输出:ND(PD∪{N,F},TD∪{tf},PreD,PostD,M0,D,Σo,lD,InD).
步骤1根据定义3构造GD.
步骤2将GD转换为Petri网.
步骤2.1对于每个状态xi∈XD,创建一个对应的库所pi∈PD.
步骤2.2对于每个库所pi∈PD,若对应的状态xi有δD(xi,σ),则创建一个变迁tj∈TD并分配标签lD(tj){σ},令PreD(pi,tj)1.对于所有的xl∈δD(xi,σ),令PostD(tj,pl)1.
步骤2.3对于所有pi∈PD,若对应的状态xi∈x0,D,则令M0,D(pi)1,否则M0,D(pi)0.
步骤3构造ND.
步骤3.1对于每个库所pi∈PD,若对应的状态xi∈XD有Γ(xi)∩ΣoΣo,则创建一个变迁
步骤3.2创建一个变迁tf,创建库所N和F.令lD(tf){λ},PreD(N,tf)PostD(tf,F)1.
步骤3.3对于所有pi∈PD,若对应的状态xi∈XDXm,D,则令InD(pi,tf)1,否则令InD(pi,tf)0.
步骤3.4令
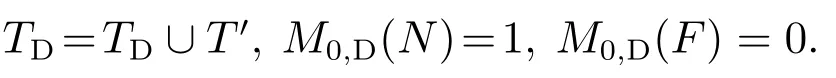
步骤3.5所有未定义的PreD(p,t),PostD(t,p),令PreD(p,t)0,PostD(t,p)0.
步骤4算法结束.

图5 自动机GDFig.5 Automaton GD
为了获得GD的状态估计,规定当GD处于状态xi时,对应的库所pi有一个令牌,否则,pi没有令牌,即每个库所只有一个令牌或没有令牌.因此,规定ND为一个二元Petri网.
定理2给定一个离散事件系统G,一个模式故障集K及其模式故障类型,记L(G)L,
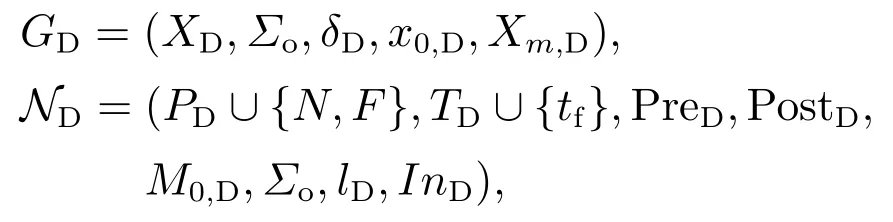
若L关于K是S型(或T型)模式故障可诊断的,则对于任意的u∈P(L),diag{u}F当且仅当Mu(F)1.
证由定理1的证明可得

根据定理2,用Petri网诊断器对系统进行在线诊断的过程中,当库所F中有一个令牌时,可以判定系统出现了故障.
算法2基于Petri网诊断器ND的模式故障在线诊断算法.
输入:
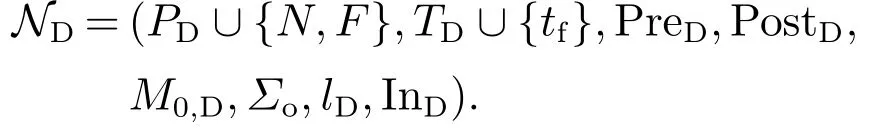
输出:Mu(F).
步骤1初始化系统,令uωσσ′ε,
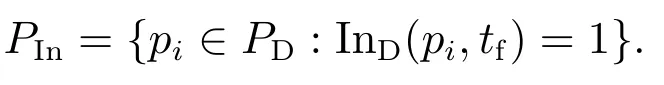
步骤2记录系统事件σ,当σσ′,跳转到步骤3.
步骤3令uωσ,对于所有ti∈TD,若
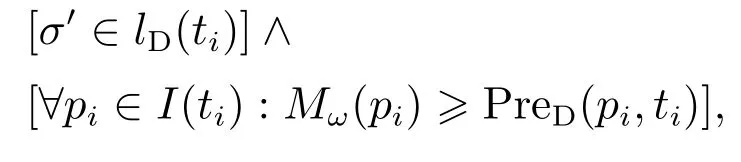
则ti发生.
步骤4对于所有∀pi∈I(ti)∪O(ti),进行计算Mu(pi).
步骤5若所有pi∈PIn都有Mu(pi)0,则有Mu(F)1,否则Mu(F)0.
步骤6令σ′σ, ωωσ.
步骤7若Mu(F)1则算法结束,否则跳转到步骤2.

转移数在最坏的情况下为
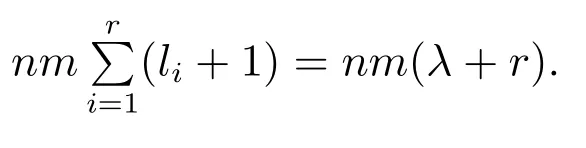
GD的状态数和转移数与G′相同.Petri网诊断器ND由GD转换得到的Petri网构造而成,在最坏的情况下,ND的库所数与抑制弧数相同,为
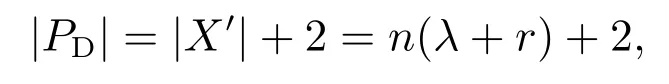
变迁数为

有向弧数为n(2m+1)(λ+r)+2.
因此,算法1步骤1的复杂性(即构造GD的复杂性)为O(λnm);步骤2的复杂性(即将GD转换为Petri网的复杂性)与构造的复杂性相同;步骤3的复杂性(即构造诊断器ND的复杂性)为O(λnm).综上可得,算法1的复杂性为O(λnm),它与系统的状态数和事件数为线性关系.
例2考虑图1的离散事件系统G,根据算法1构造Petri网诊断器ND如图6所示.
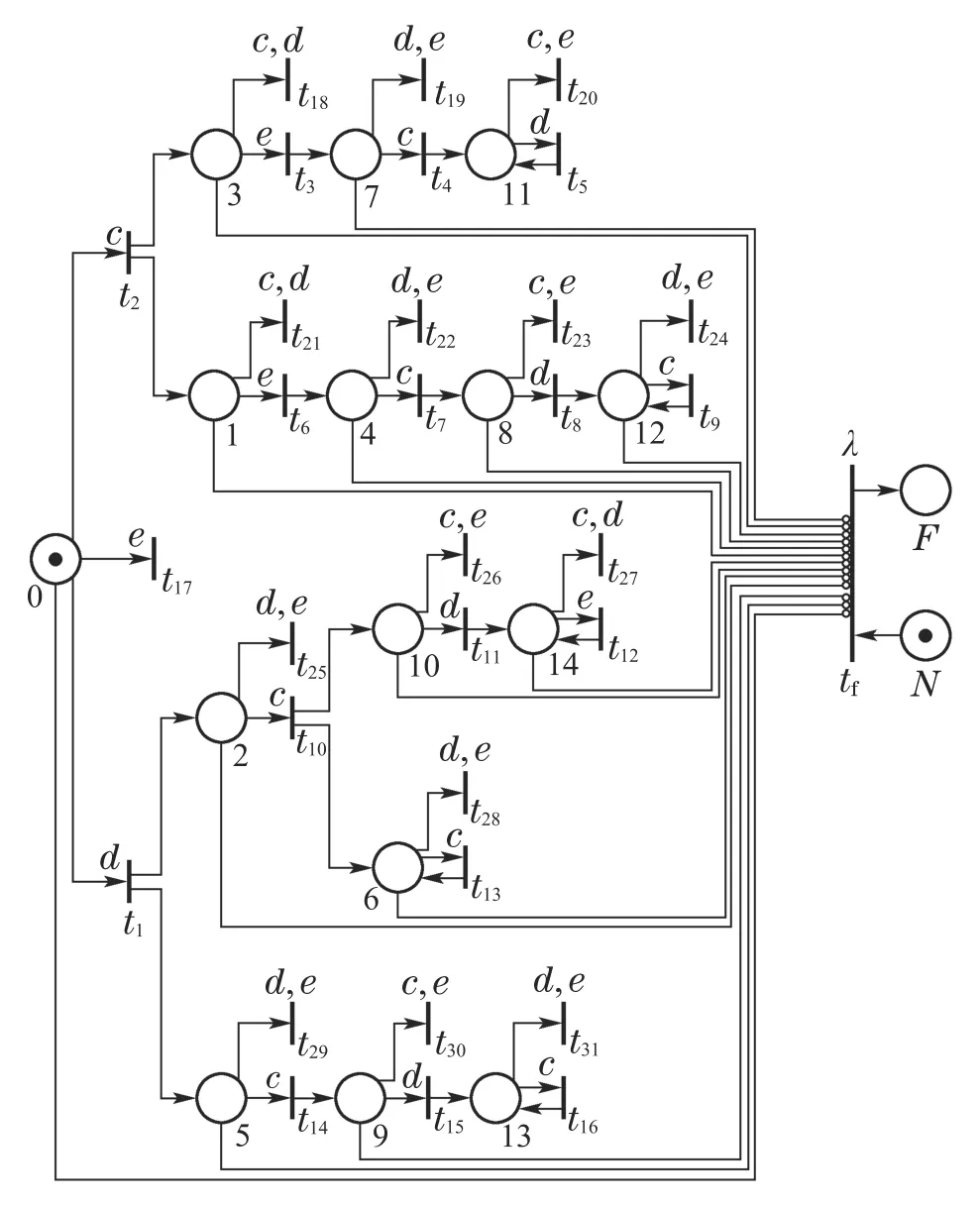
图6 Petri网诊断器NDFig.6 Petri net diagnosers ND
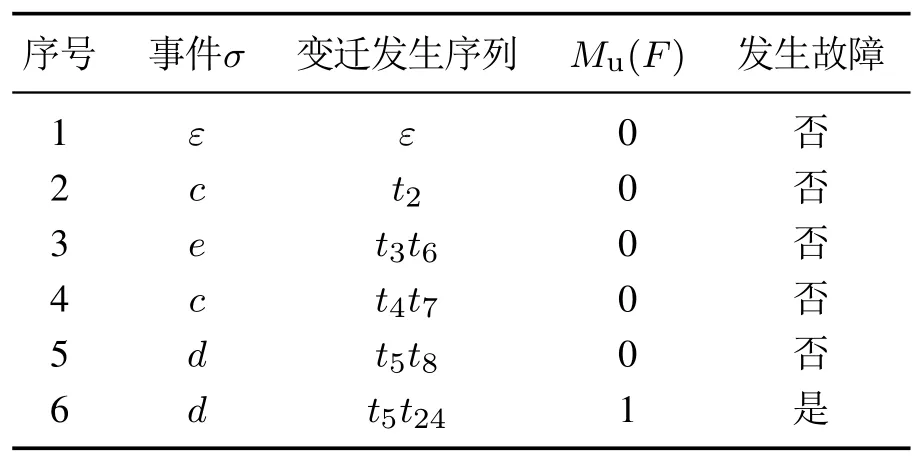
表1 诊断结果Table 1 Diagnostic result
5 总结
本文研究了离散事件系统的模式故障在线诊断问题,提出自动机GD可用于S型模式故障和T型模式故障在线诊断.根据GD提出Petri网诊断器ND的构造算法及在线诊断算法.本文提出的Petri网诊断器具有多项式的空间复杂性,在在线诊断的过程中根据库所的令牌数便可判断系统是否发生了故障,具有所需储存空间小、效率高等优点.
