突发交通事件对山区高速公路交通运行影响的VISSIM仿真分析及预测

郑 楠，杨文臣，马 力，韩 辉

(1.云南省交通规划设计研究院有限公司陆地交通气象灾害防治技术国家工程实验室，云南 昆明 650031；2.交通运输部公路科学研究院，北京 100088)

我国高速公路快速化、规模化和网络化发展带来了较为严重的交通事故、交通拥堵和交通污染等问题，道路交通安全形势不容乐观，尤以不利天气、重大交通事故、大范围交通拥堵等突发交通事件对山区高速公路网的交通运行安全和可靠性的挑战最为突出[1]。突发交通事件对高速公路交通运行态势影响的定量化、精细化研判是快速响应和及时处置突发交通事件的关键，是高速公路交通安全防控和应急管理研究中迫切需要解决的研究热点和实践难题。

交通事件对高速公路交通运行态势的影响分析方法可分为三类，即历史数据实证研究方法、数值模拟方法和交通仿真分析方法。历史数据实证研究方法[2-4]以历史交通事件数据、交通流数据、交通事故数据为基础，采用描述性统计分析方法或多元非线性回归等数理统计模型，定量研究交通事件对高速公路交通流和交通运行安全的宏观影响。数值模拟方法根据突发交通事件下交通运行机理，采用交通流理论与建模技术，构建交通事件条件下车辆跟驰、换道等数学模型，分析不同交通事件下交通运行态势的时空变化规律，其中以离散的元胞自动机模型的应用最为广泛[5-7]。交通仿真分析方法[8-10]根据突发交通事件下道路条件、交通流条件和驾驶行为，采用VISSIM、PARAMICS、CORSIM等微观交通仿真软件，建立了道路交通流仿真模型，通过在线或离线仿真模拟不同实验场景下高速公路的交通流运行，可视化研判突发事件对交通系统的影响。历史数据实证研究方法需要丰富的历史数据，且宏观预测模型移植的精度有限；数值模拟方法基于一定假设，建立了中观交通流的动力学模型，但受限于实际交通系统的复杂性、时变不确定性，难以建立精确的数学模型描述交通事件；而VISSIM等微观交通仿真软件，作为一种无偏的评价工具，已被广泛应用于交通事件的理论研究和工程应用中。

本文以山区高速公路复杂的桥隧群区段为研究对象，提出了一种基于VISSIM的突发交通事件对山区高速公路交通运行影响的仿真分析与建模方法，分析了不同交通流量、封闭车道数和事件持续时长下突发山区高速公路交通运行态势的时空演化规律，并建立了最大排队长度预测模型，可为突发交通事件应急管理提供参考。

1 突发交通事件仿真建模

1.1 交通安全影响分析方法比较

(1) 历史数据实证研究方法[2]是一种事后统计分析方法，需要有大量的高质量历史交通数据，且由于交通事件对高速公路交通运行影响的范围及程度表现出较强的时空异质性，因此需要强化本地化建模与分析方法。

(2) 数值模拟方法[6]是基于机理的数学建模分析方法，这种方法的理论性和逻辑性完备，但是由于交通系统是一个复杂、开放的巨系统，交通事件对高速公路交通运行的影响因素众多，难以建立精确、统一的数学模型，因此如何提取交通事件对高速公路交通运行影响的重要特征因子，并建立合适的交通事件影响预测模型是该方法面临的重要挑战，且这种分析方法需要较强的数学基础，目前理论研究应用较多，工程应用研究相对较少。

(3) 交通仿真分析方法[10]无须从微观交通流建模分析入手，可直接利用交通仿真软件中成熟的交通流模型，快速构建应用对象的仿真模型，可视化和定量分析交通事件对交通运行的影响，适用于“事前、事中和事后”的全过程交通影响分析，但如何通过交通仿真参数校准等构建逼近“真实”的交通场景是该方法结果有效性的关键，适合于快速工程应用。

1.2 交通事件分类及仿真配置

影响交通安全和通行效率的交通事件多指非重现的交通事故、临时交通管制、雨雾冰雪等不利天气及其组合事件。根据高速公路交通事件的灾害类别及特点，交通事件可分为单点事件、路段事件和区域事件，典型高速公路交通事件分类及仿真配置需求见表1[11-13]。

表1 典型高速公路交通事件分类及仿真配置需求Table 1 Classification and simulation configuration of typical highway traffic incidents

1.3 交通事件的VISSIM仿真建模

1.3.1 交通事件仿真模拟的关键问题

突发交通事件下，路段乃至路网的交通环境发生了改变，并导致交通流和驾驶行为发生了相应的变化。突发交通事件下高速公路交通运行仿真模拟的关键问题包括三个方面：一是交通事件模拟，建立典型的突发交通事件仿真模型，能够可视化模拟各类突发交通事件对高速公路交通运行造成的影响；二是交通事件影响分析，支持输出排队长度、延误、通过量、速度、交通冲突等结果数据，选取合理的评价指标分析突发交通事件对高速公路交通运行影响的时变特性；三是交通运行影响态势预测，提取突发交通事件对高速公路交通运行影响的重要特征变量，建立交通运行影响范围预测模型，分析高速公路交通运行态势的演化趋势。

1.3.2 交通事件的VISSIM仿真建模流程

VISSIM是一种可视化的微观交通仿真软件，能对单一车辆行驶特性和驾驶行为进行微观处理，并可模拟、分析和评价实际道路上交通流的运行，作为一种无偏的技术手段，VISSIM已被广泛应用于交通工程应用研究。本文利用VISSIM仿真软件，开发了高速公路交通运行仿真实验平台，对不同交通流条件下突发交通事件的影响因素进行了定量的仿真评价和分析。高速公路突发交通事件的VISSIM仿真建模流程主要包括：基础路网仿真建模(几何结构)、仿真模型参数校准(行为参数)、交通事件仿真模拟、交通运行仿真模拟和仿真结果统计(评价指标)，详见图1。

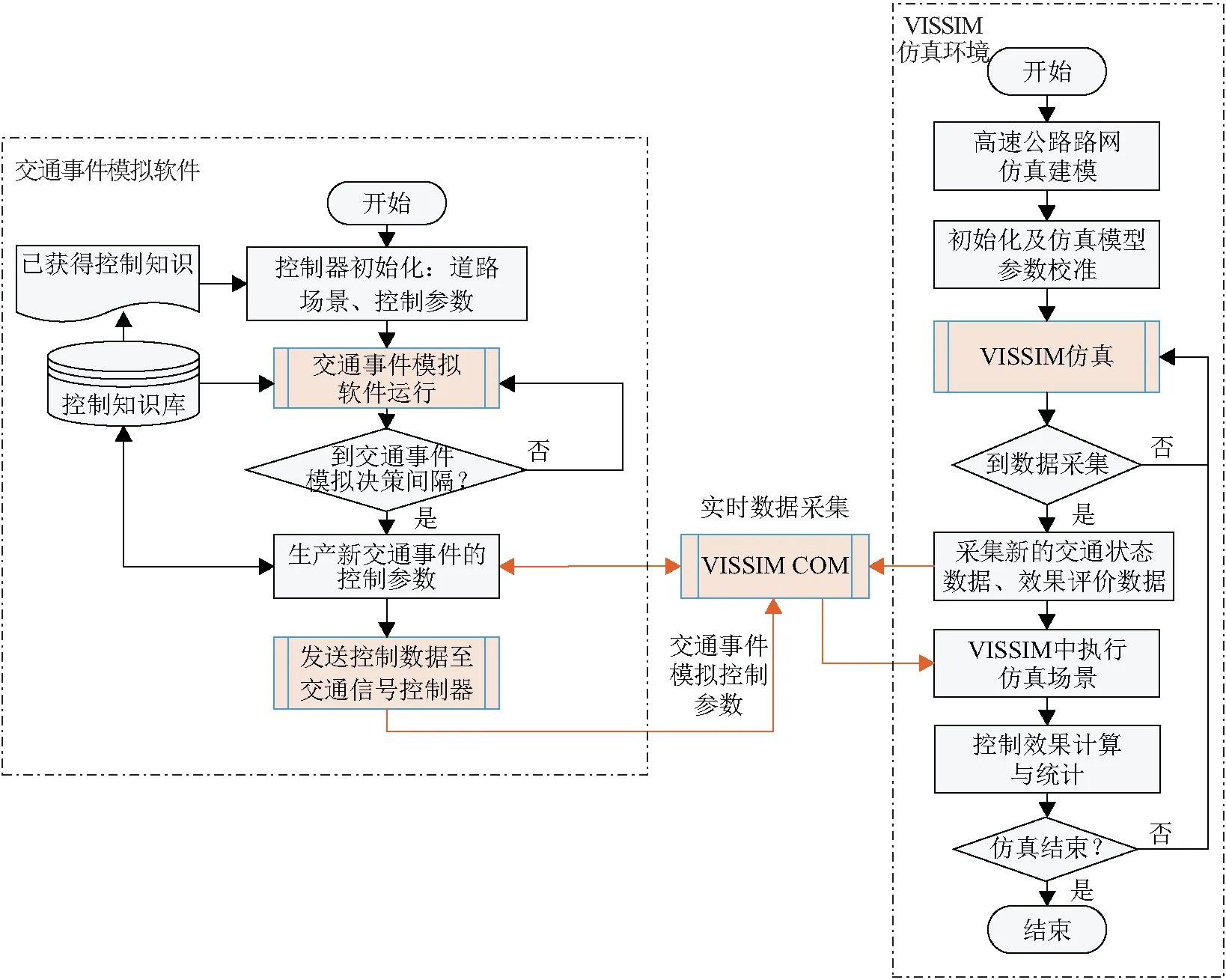
图1 高速公路突发交通事件的VISSIM仿真建模流程Fig.1 VISSIM simulation procedure of emergent traffic incidents on highway

根据具体的交通事件特性，确定调整的仿真模型参数和模拟方法，而针对突发交通事件和特殊路段交通运行的仿真模拟主要通过调整仿真模型中交通流参数、驾驶行为参数、道路控制参数或车辆参数来实现。其中，车辆参数包括行驶速度、加速度、减速度等；驾驶行为参数包括跟驰、换道行为、车头时距等；交通流参数包括OD流量和期望速度等；道路控制参数包括车道关闭、行驶路径等。

2 应用案例与实验设计

2.1 案例描述

受光照条件、结构物空间、交通环境、不利天气等多种因素的影响，山区高速公路桥隧密集区的行车条件会发生频繁变化，随着交通流量的增加，桥隧密集区已逐渐成为山区高速公路事故多发路段。故本文选取云南某山区高速公路的桥隧密集区段(K35～K47)为研究对象，该路段共含2座桥梁和5条隧道，桥隧比高达90%，采用双向四车道分离式设计，设计车辆行驶速度为80 km/h，隧道内车辆限速为60 km/h，行车安全隐患较为突出。对隧道路段的模拟，要根据设计车辆行驶速度，通过在该隧道路段突发交通事件VISSIM仿真模型中设置起始/终点断面并分别设置期望速度决策点来实现。

图2 山区高速公路桥隧路段突发交通事件VISSIM仿真模型Fig.2 VISSIM simulation model of mountainous highway bridge-tunnel group section

2.2 参数校定

以通行能力为指标，根据渝昆高速公路设计的车辆行驶速度、通行能力和大小型车辆构成，通过调整驾驶行为参数并多次仿真[14]，使该路段通行能力达设计通行能力的95%以上。经过多次试验，Wiedemann99模型参数的标定结果如上：CC0(停车间距)为1.5 m，CC1(车头时距)为2.5 s，CC2(跟车变量)为4.0 m，CC3(进入跟车状态的阀值)为-8.00，CC7(加速度波动幅度)为0.25 m/s2，最大前视距离为250.0 m。

2.3 实验设计

假定在A和B两个隧道间(K400+100)发生交通事故，通过配置不同的事件持续时长(即事件持续时长)t、封闭车道数N和交通流量V，模拟不同的交通事件场景，VISSIM仿真实验方案设计见表2。其中，仿真预热时间取15 min，事件发生的时间点为仿真900 s，大车率为0.3。在仿真路段范围内设置排队计数器(Queue Counter)和数据采集器(Data Collection)采集交通事件条件下车辆的排队、行驶速度、通过量等数据。其中，排队计数器布设在事件发生地点上游20 m处，数据采集器在事故发生地点，上游布设35个断面，下游布设2个断面。

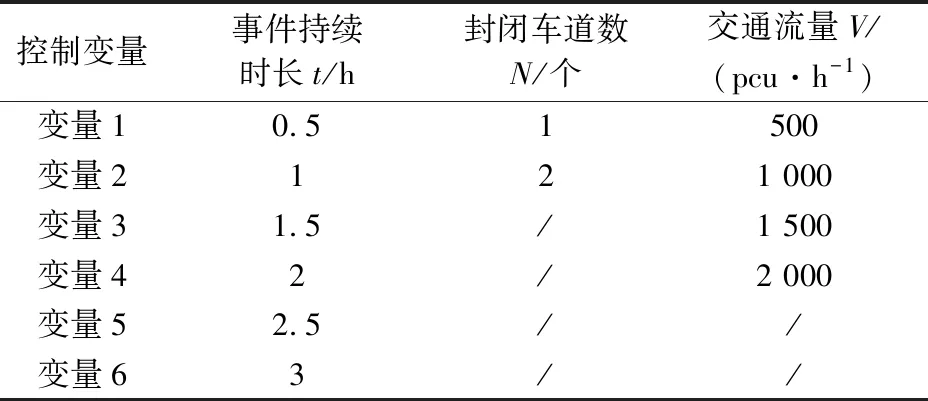
表2 VISSIM仿真实验方案设计Table 2 Experiment plan of VISSIM simulation

3 突发交通事件对山区高速公路交通运行的影响与态势演化特征分析

3.1 不同事件持续时长的影响

本文以封闭1个车道、交通流量为1 500 pcu/h的突发交通事件为例，利用VISSIM仿真模型模拟得到了不同事件持续时长(t)下车辆行驶速度的时空分布图，见图3。图中颜色图谱表征车辆行驶速度，深红色表示行驶速度低，绿色表示行驶速度高。

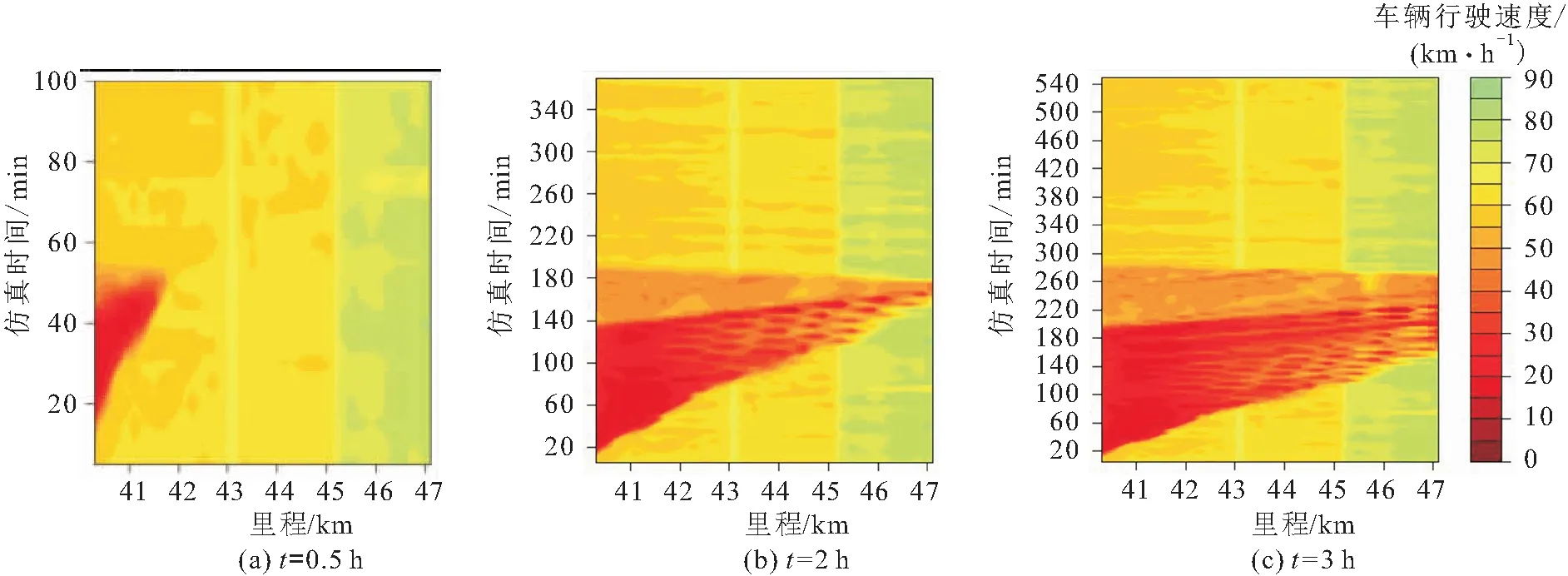
图3 不同事件持续时长下车辆行驶速度时空分布图(N=1个，V=1 500 pcu/h)Fig.3 Spatial-temporal distribution of the driving speed with different incident duration (N=1，V=1 500 pcu/h)

由图3可见，在交通事故发生时(15 min)，离事故发生地点最近的断面开始出现拥堵，车辆行驶速度开始大幅下降至0，此后，事故路段上开始出现排队，并以集结波的形式迅速向上游蔓延；当交通事故消除后，事故发生地点通行能力恢复，离事故发生地点最近的断面开始出现消散波，由于消散波的速度大于到达集结波的速度，两者交汇处为最大排队长度，之后车辆行驶速度逐渐恢复至正常水平。

本文利用VISSIM仿真模型模拟得到了不同事件持续时长(t)下事故路段车辆平均行驶速度(v)和最大排队长度(LQ)的分布曲线，见图4。

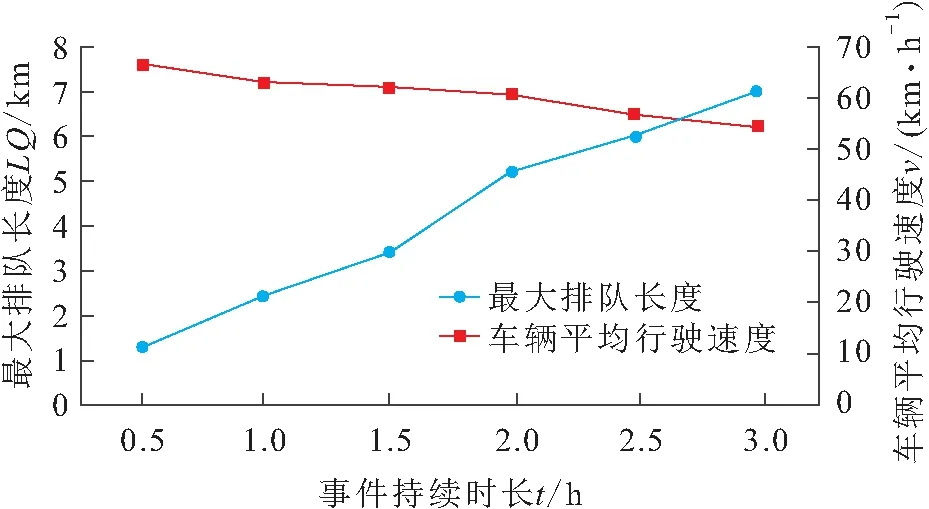
图4 不同事件持续时长下事故路段车辆平均行驶 速度和最大排队长度的分布曲线Fig.4 Curves of the average driving speed and the maximum queue length with different incident duration

由图4可见，当封闭车道数和交通流量一定时，离事故发生地点最近的断面车辆平均行驶速度与事件持续时长呈线性负相关关系，最大排队长度与事件持续时长呈线性正相关关系，即事件持续时长越长，受影响时段内路段上车辆平均行驶速度越低，最大排队长度越大，交通流运行条件越差。

事故路段上车辆平均行驶速度、最大排队长度与事件持续时长的线性拟合关系式如下：

LQ=1 194.1t,R2=0.992 3

v=-2.362 9t+68.753,R2=0.975 2

(1)

式中：LQ为最大排队长度(m);v为车辆平均行驶速度(km/h);t为事件持续时长(h)。

由公式(1)可知，R2均大于0.97，表明关系模型的线性拟合度好。

3.2 不同封闭车道数的影响

本文以交通流量为500 pcu/h、事件持续时长为1 h和2 h的突发交通事件为例，利用VISSIM仿真模型模拟得到了不同封闭车道数下车辆行驶速度的时空分布图，见图5。

由图5可见，当交通事故阻断1个车道时，路段上剩余车道的通行能力能满足交通流量，不同事故条件下路段上车辆行驶速度没有明显变化；当事故阻断2个车道时，路段完全中断，车辆行驶速度表现为事故发生时快速下降、事故清除后快速上升，且车辆行驶速度下降-上升的时空影响范围与事件持续时长呈正相关。这是因为受影响车道数与路段上剩余车道的通行能力呈负相关，而剩余车道的通行能力与交通流量的关系直接决定着交通流的运行状态，但是只考虑剩车道的余通行能力而忽视交通流量，无法客观地分析突发交通事件对高速公路交通运行的影响与态势演化特征。

图5 不同封闭车道数下车辆行驶速度的时空分布图(V=500 pcu/h)Fig.5 Spatial-temporal distribution of the driving speed with different closed lane numbers (V=500 pcu/h)

3.3 不同交通流量的影响

本文以封闭2个车道、事件持续时长为0.5 h的突发交通事故为例，利用VISSIM仿真模型模拟得到了不同交通流量下车辆行驶速度的时空分布图，见图6。

由图6可见，在事件持续时长和封闭车道数确定的情况下，交通流量越大，车辆行驶速度降低的断面就越多，交通拥堵消散(车辆行驶速度恢复)的时间也越长；当到达的交通流量(2 000 pcu/h)远大于道路通行能力时，仿真时空范围内(仿真时长-里程)甚至无法观测到完整的车辆行驶速度“下降—上升”的过程，交通事件对高速公路交通流的影响极为严重，高速公路接近“交通中断”。

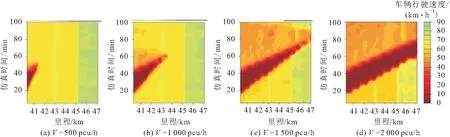
图6 不同交通流量下车辆行驶速度的时空分布图(N=2，t=0.5 h)Fig.6 Spatial-temporal distribution of the driving speed with different arriving traffic volume (N=2，t=0.5 h)

本文利用VISSIM仿真模型模拟得到了不同交通流量下事故路段车辆平均行驶速度和最大排队长度的分布曲线见图7。

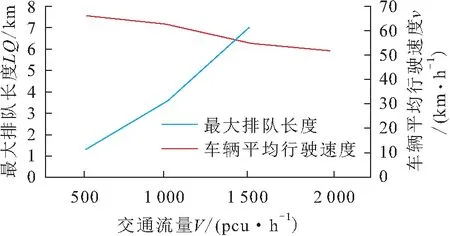
图7 不同交通流量下事故路段车辆平均行驶速度和 最大排队长度的分布曲线Fig.7 Curves of the average driving speed in the accident highway section and the maximum queue length with different traffic volume

由图7可见，突发交通事件影响范围内事故路段上车辆平均行驶速度、最大排队长度与交通流量的线性拟合结果表明：车辆平均行驶速度与交通流量呈线性负相关关系，线性拟合度好(R2=0.974)；最大排队长度与交通流量的线性拟合度较好(R2=0.903)，表现出幂函数关系。

事故路段上车辆平均行驶速度和最大排队长度与交通流量的线性拟合关系式如下：

LQ=2 094V，R2=0.903

v=-5.14V+72.55,R2=0.974

(2)

式中：V为交通流量(pcu/h)。

4 基于最大排队长度的交通运行影响范围预测模型

4.1 交通运行影响范围预测及指标选取

最大排队长度是集结波和消散波速度达到均衡时的排队长度，可直观地表征突发交通事件对高速公路交通流运行影响的空间范围和严重程度。本文选取最大排队长度作为评价指标，通过筛选其重要影响因素，构建了最大排队长度的预测模型，并采用仿真实验数据估计模型参数，预测突发交通事件对高速公路交通流运行的影响，研判其演化态势。

4.2 最大排队长度预测模型建立

根据上述不同道路交通条件下突发交通事件对高速公路交通流运行影响的分布特征(见图3至图7)分析可知，最大排队长度与交通事件持续时长、封闭车道数呈正相关的线性关系，最大排队长度与交通流量呈正相关的幂函数关系。最大排队长度预测模型建立的原理如下：①定义最大排队长度为因变量，事件持续时长、封闭车道数和交通流量为自变量；②采用累乘法综合表征3个自变量对最大排队长度的累积交互效应；③由于最大排队长度与交通流量间存在幂函数关系，在不改变最大排度长度与事件持续时长、封闭车道数和常数项3个变量间关系规律的同时，分别对其进行自然指数的变换，以采用“简单、适用”的线性回归估计最大排队长度预测模型的参数。因此，最大排队长度预测模型采用指数函数和幂函数的组合模型形式，其基本模型如下：

LQ=ea0·ea1N·ea2t·Va3

(3)

式中：N为封闭车道数(个)；a0为模型常数项系数；a1、a2、a3为模型自变量系数。

对公式(3)进行对数变换，则最大排队长度对数的多元线性回归预测模型为：

ln(LQ)=a0+a1N+a2t+a3ln(V)

(4)

采用最小二乘法对公式(4)的多元线性回归模型进行参数估计，模型参数估计和显著性检验结果，见表3。

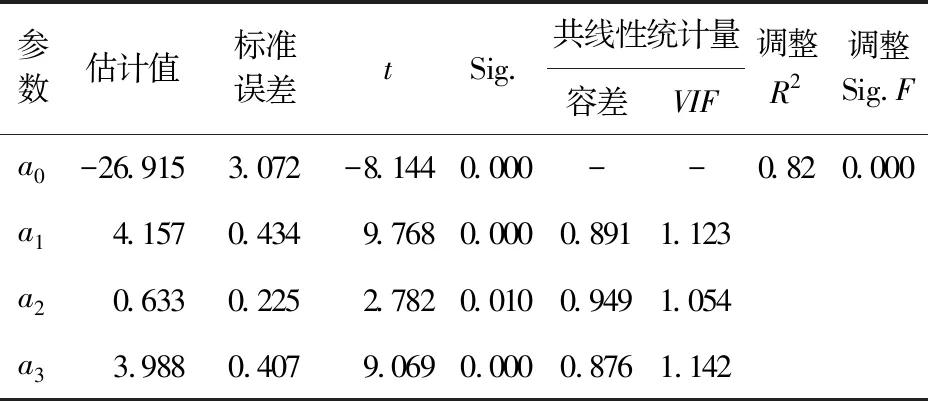
表3 最大排队长度预测模型参数估计和显著性检验结果Table 3 Parameters estimation and significance test result of the maximum queue length predictive model

由表3可知，调整R2达到0.820，表明模型拟合优度可接受；模型显著性F检验结果显示，Sig.值为0.000，拒绝F检验的原假设，表明拟合的模型具有统计学意义。

经参数估计后的最大排队长度预测模型如下：

lnLQ=-26.915+4.157N+0.633t+3.988lnV,R2=0.82

(5)

该预测模型形式简单、实用，可解释突发交通事件条件下最大排队长度对数值的82%变化，具有较好的工程适用性。

对公式(5)进行自然指数变换，由于最大排队长度的对数值存在拟合误差，经自然指数转换后该误差将被指数级放大，故采用修正系数f对误差进行修正，修正后的最大排队长度预测模型如下：

LQ=f·e-26.915·e4.157N·e0.633t·V3.988

(6)

上式中的修正系数f在实际应用中须采用实际最大排队长度数据进行标定，但由于缺乏突发交通事件下实测的最大排队长度数据，故本文采用仿真最大排队长度进行标定，f的计算值为2.123，R2为0.973，说明建立的最大排队长度预测模型拟合精度好，具有明显的统计意义。

本文以实验路段20%的仿真实验数据作为基准，检验本文建立的最大排队长度预测模型[见公式(6)]预测结果的准确性。最大排队长度预测与仿真结果的对比，见图8。

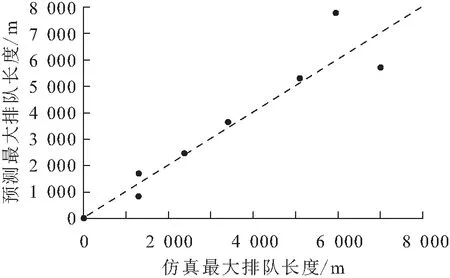
图8 最大排队长度预测与仿真结果的对比Fig.8 Comparison between the predicted and simulated maximum queue length

由图8可见，预测模型的预测值向45°参照线集中，平均绝对相对误差为23.24%，与45°参照线偏离的误差较稳定，说明最大排队长度预测模型的准确性较好。

5 结 论

(1) 系统梳理了交通事件下高速公路交通运行态势影响分析的三类方法，包括历史数据实证研究方法、数值模拟方法和交通仿真分析方法，归纳了其技术特征，分析了其关键问题和适用边界；归纳了高速公路交通事件类型及仿真需求配置，从“简单、快速”的工程应用角度，提出了一种基于VISSIM的突发交通事件对山区高速公路交通运行影响的仿真分析与建模方法。

(2) 提出了突发交通事件VISSIM仿真实验场景设计方法。以云南某山区高速公路事故多发的桥隧群区段为研究对象，提出了仿真模型参数标定的准则及标定结果，并通过控制事件持续时长、封闭车道数和交通流量3个变量的变化，模拟了不同突发交通事件仿真场景。

(3) 分析了不同事件持续时长、封闭车道数、交通流量下突发交通事件对山区高速公路交通流的影响与运行态势的演化特性，结果表明：最大排队长度与交通流量表现出正相关幂函数关系，而最大排队长度与事件持续时长、封闭车道数表现出线性正相关关系。

(4) 采用指数函数和幂函数的组合形式，提出了最大排队长度预测模型的基本形式，并采用最小二乘法估计模型参数，结果表明：预测模型的拟合度和显著性较高，可预测约80%的最大排队长度变化，且该模型的对数形式是简单的多元线性回归模型，具有较好的工程实用性，但预测模型的实际预测精度仍需在实践中利用实测数据进一步检验。