风化花岗岩隧道矿山法施工地下水渗流特征与防水技术研究
2020-08-14胡文艺陈令强罗其奇朱六兵陈建平
胡文艺,陈令强,罗其奇,冯 勇,朱六兵,陈建平
(1.广州地铁集团有限公司,广东 广州 510220;2.中南大学土木工程学院,湖南 长沙 410075;3.中铁十九局集团有限公司,北京 100176;4.中国地质大学(武汉)工程学院,湖北 武汉 430074)
隧道工程建设会打破原有的地下水环境平衡状态,造成地下水资源流失,对地下与地表生态环境产生不良的影响,而隧道突涌水也严重危害了隧道施工安全[1-3]。相较于盾构法和TBM施工,矿山法施工会对隧道围岩造成更严重的扰动和损伤,形成明显的开挖损伤区,使该区域内的围岩渗透性增强,进一步加剧地下水资源流失,包括造成地下水水位下降和地下水水质变化等,对隧道沿线村庄耕地、植被等生态环境产生不良的影响[4-6]。
目前国内外学者针对隧道建设与地下水环境之间的相互影响关系已进行了大量的研究。如Raposo等[7]将地下水平衡模型运用于地下水环境分析中,改进了隧道施工工艺和防排水结构,降低了隧道施工对地下水的影响;刘志春等[8-9]在裂隙岩体隧道中研究了隧道施工与地下水环境之间的相互影响机理,为地下水环境保护提供了理论依据。
但是,当前关于隧道建设与地下水环境之间相互作用的分析主要集中在岩溶隧道,很少涉及风化花岗岩矿山法施工隧道,也较少考虑矿山法施工措施及不同防排水结构等因素的影响。为了避免矿山法施工中可能遇到的隧道突涌水灾害,本文以风化花岗岩隧道为工程背景,通过现场监测和数值模拟手段,研究了风化花岗岩隧道在矿山法施工条件下地下水的渗流规律,并通过不同防水结构下流固耦合特征的分析,探讨了不同防水结构下地下水对二次衬砌的影响,在此基础上考虑地下水环境变化,在代表性断面处提出了合适的防水控制措施,该研究成果可为隧道矿山法防水施工提供技术依据,具有重要的实际应用价值。
1 工程概况
广州地铁21号线长平站—金坑站区间,隧道为双洞单线隧道,地形起伏大,地下水水位埋藏差异较大,地下水水位的变化与地下水的赋存、补给和排泄关系密切,并受大气降水和季节变化的影响严重。
该地铁隧道所处的地层主要为花岗岩全风化带、花岗岩强风化带、花岗岩中风化带、花岗岩微风化带,风化花岗岩颗粒粗、孔隙率大、透水性强,基岩整体局部破碎,工程性质一般,地下水为孔隙水和基岩裂隙水,富水性强,地下水水头高度最高约为115 m,研究区域纵剖面见图1。地铁隧道主要采用以防为主的指导思想,通过全包防水结构和控制性全包防水结构来控制地下水流失,两种防水结构均全断面布置了一层致密的防水板,区别在于控制性全包防水结构在拱脚处设置了排水盲管。
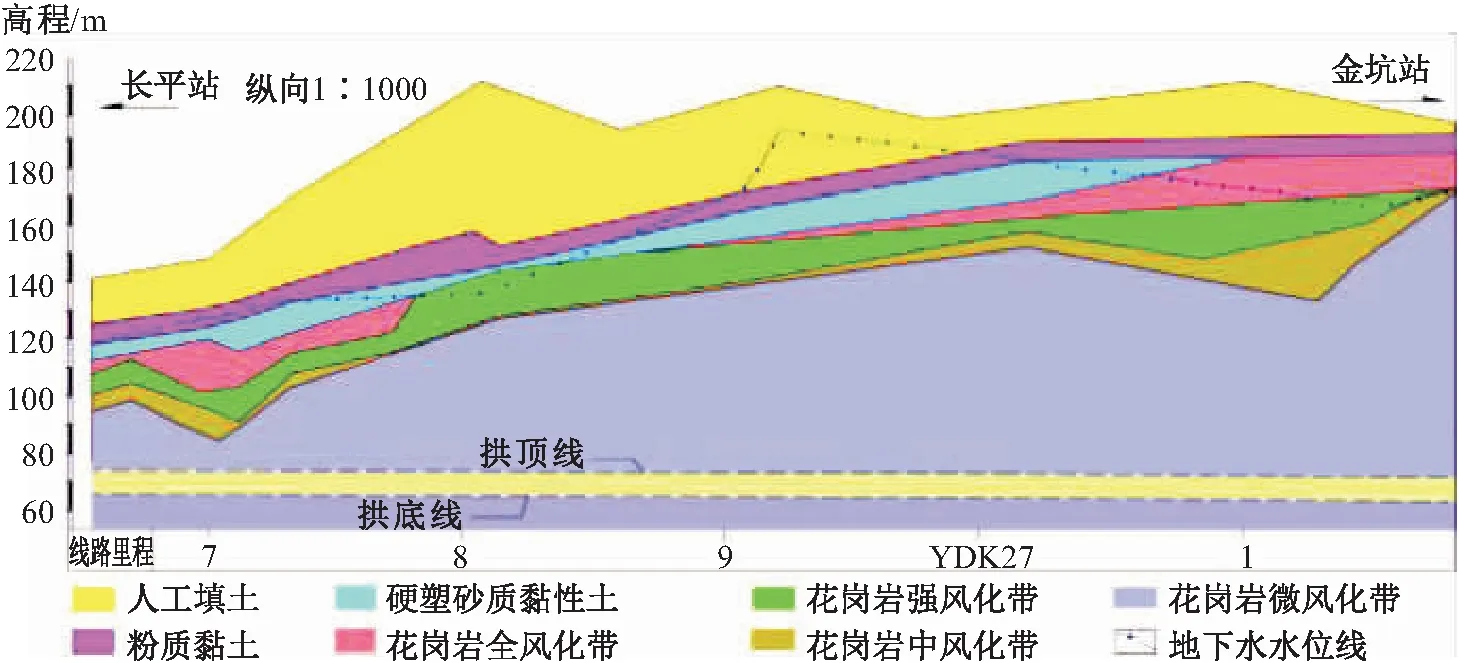
图1 研究区域纵剖面图Fig.1 Longitudinal section diagram of the research area
2 风化花岗岩隧道在矿山法施工条件下地下水的渗流特征分析
2.1 计算模型
为了便于研究,对风化花岗岩地层条件进行了适当简化,计算模型中隧道断面采用Ⅲ级围岩复合式衬砌标准断面,见图2,采用全包防水结构。复合式衬砌主要参数为:初期支护采用100 mm厚C25喷射混凝土;二次衬砌采用300 mm厚C40模筑钢筋混凝土。
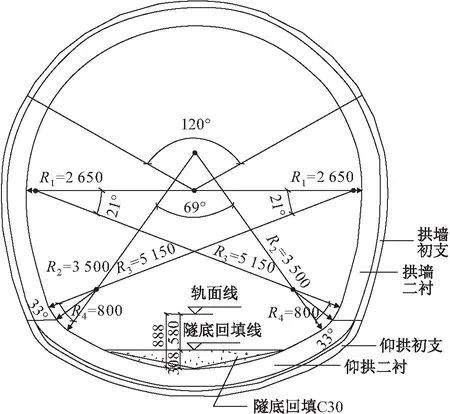
图2 隧道Ⅲ级围岩复合式衬砌标准断面设计图 (单位:mm)Fig.2 Design diagram of the standard section of the composite lining of Ⅲ-grade surrounding rock (Unit:mm)
采用ABAQUS数值模拟软件建立隧道瞬态渗流模型,对风化花岗岩隧道矿山法施工过程中不同施工阶段的地下水渗流场进行瞬态分析,模型宽500 m、高200 m,隧道埋深50 m。使用四边形孔压实体单元(CEP4P)对计算模型进行网格划分,隧道界限附近15 m范围局部加密,计算模型网格剖分见图3。隧道施工采用矿山法施工中的全断面开挖法,工序依次为拱墙开挖、拱墙支护、仰拱开挖、仰拱支护、仰拱衬砌、拱墙衬砌。
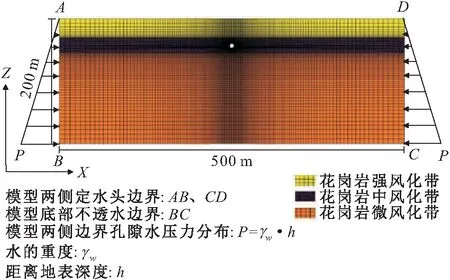
图3 隧道瞬态渗流模型示意图Fig.3 Schematic diagram of tunnel transient seepage flow model
2.2 渗流计算基本原理
(1) 达西定律:达西以饱和砂土为渗流介质,进行了地下水渗透试验,得出了达西定律。达西定律的表达式如下:
(1)
式中:Q为单位时间地下水渗流量(m3/d);L为地下水渗流路径长度(m);K为含水层渗透系数(m/d);h为地下水总水头损失(m);A为地下水过水断面面积(m2)。
(2) 渗流基本方程:地下水在渗流过程中,满足质量守恒定律,有如下的渗流连续性方程:
(2)
式中:S为水头变化单位高度时,从单位体积含水层中存储或释放的水量(m3);v为流速(m/s);t为时间(s)。
2.3 模型计算参数与边界条件
初始地下水水位位于地表处,取隧道水平面内平行于地表方向为X轴,垂直于地表方向为Z轴。模型力学边界条件为:限制模型两侧边界X向位移,限制底部边界位移。模型渗流边界条件为:模型两侧边界孔隙水压力沿深度分布,为定水头边界;模型底部为不透水边界,左右边界孔隙水压力固定,地下水水位保持动态变化。
根据勘察资料和试验资料确定的模型计算参数见表1,各计算参数分别对应图2和图3中的结构,围岩使用Mohr-Coulomb本构模型,初期支护和二次衬砌使用弹性本构模型。

表1 模型计算参数表Table 1 Table of model calculation parameters
2.4 隧道矿山法施工过程中地下水流速的变化规律
风化花岗岩隧道矿山法施工不同阶段地下水流速矢量分布,见图4。
由图4可以看出:
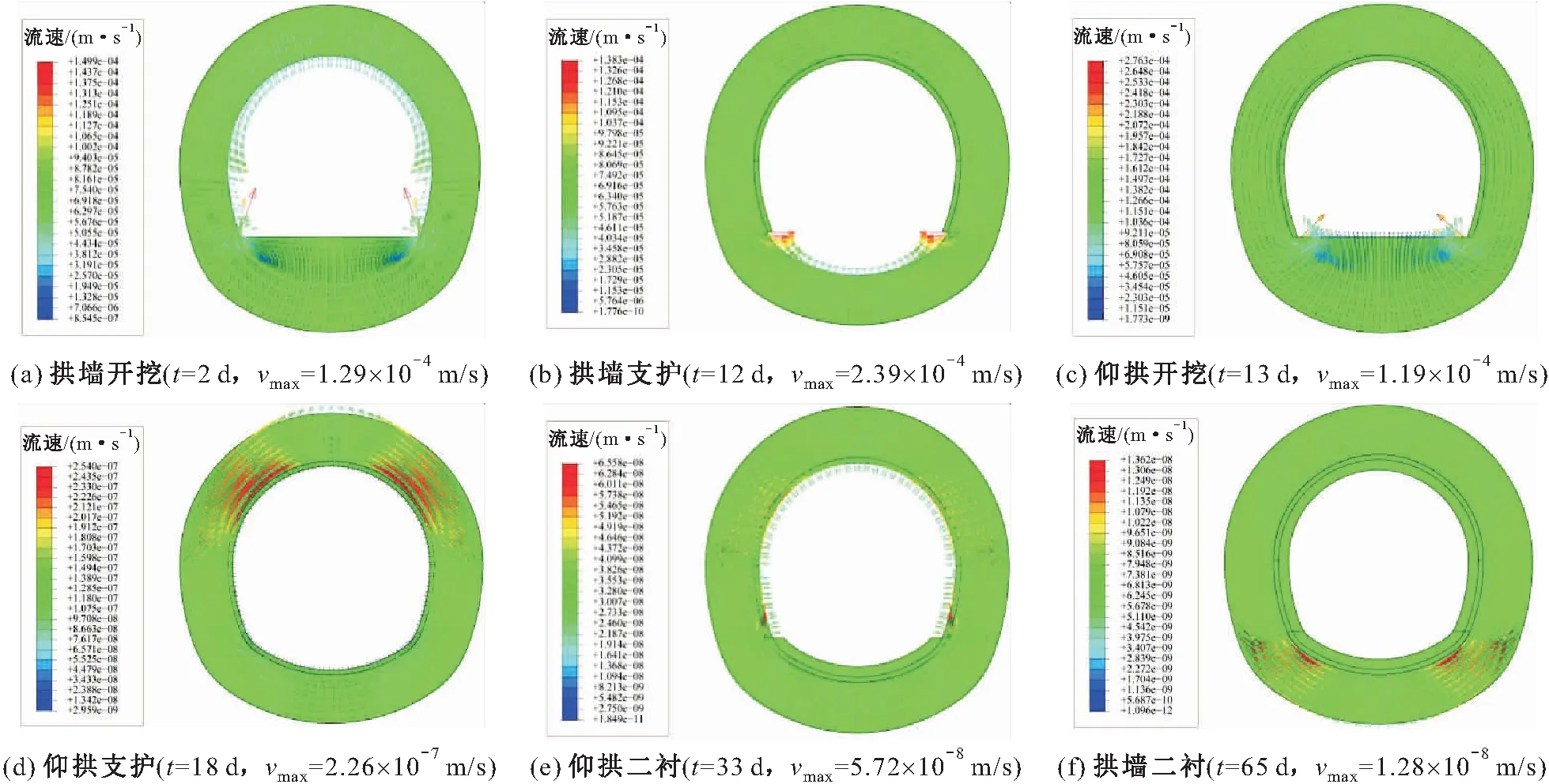
图4 风化花岗岩隧道矿山法施工不同阶段地下水流速矢量分布图Fig.4 Distribution diagram of velocity vector of groundwater flow in the weathered granite tunnel in different stages of mining method construction
(1) 拱墙开挖后(t=2 d时刻),由于开挖面的排水,地下水向开挖面集中,开挖面拱脚附近地下水流速最大,流速最大值vmax为1.29×10-4m/s;拱墙支护之后(t=12 d时刻),仰拱断面处的地下水在水压力的作用下向上渗流,地下水流速显著增大,由于支护之后排水断面减小,地下水向仰拱断面集中,仰供断面拱脚处地下水流速最大,流速最大值vmax为2.39×10-4m/s。
(2) 仰拱开挖之后(t=13 d时刻),地下水沿着初期支护结构向仰拱部分渗流,仰拱部位的地下水向隧道净空面渗流,在仰拱开挖面与支护结构的交界面处仰拱断面拱脚处地下水流速最大,流速最大值vmax为1.19×10-4m/s;仰拱支护后(t=18 d时刻),初期支护结构封闭成环,整个断面处流速显著减小,地下水环境逐渐恢复平衡,在初期支护外侧拱肩处地下水流速最大,流速最大值vmax为2.26×10-7m/s,地下水沿初期支护外侧向拱顶渗流。
(3) 仰拱衬砌之后(t=33 d时刻),仰拱处地下水渗流显著减弱,渗流方向沿仰拱流向拱顶,地下水流速继续减小,在两侧拱脚处地下水流速最大,流速最大值vmax为5.72×10-8m/s;拱墙衬砌之后(t=65 d时刻),整个隧道支护工程施工结束,地下水环境逐渐恢复,此时地下水渗流速度最小,地下水由拱顶至仰拱渗流,在仰拱部位地下水流速最大,流速最大值vmax为1.28×10-8m/s。
2.5 隧道矿山法施工过程中地下水水位的变化规律
风化花岗岩隧道矿山法施工不同阶段地下水水位变化情况,见图5,取地下水水位最低点至初始地下水水位间的距离为最大水位降深,绘制隧道矿山法施工不同阶段最大水位降深hmax随施工进程的变化曲线,见图6。
由图5和图6可见,仰拱支护期间,最大水位降深达到最大值,其值为17.37 m;拱墙开挖期间,地下水水位降深为7.96 m,占最大水位降深的45.80%;拱墙支护期间,地下水水位降深最大,达到7.96 m,占最大水位降深的45.85%;仰拱开挖期间,地下水水位降深增速减缓,地下水水位降深为1.02 m,占最大水位降深的5.87%,地下水水位下降速度明显减缓;仰拱支护期间,地下水水位下降至最大水位降深后开始上升,地下水水位在最低点处上升了2.33 m,上升速度最快,上升高度占总上升高度的15.42%;仰拱二衬期间,地下水水位上升幅度继续增加,期间地下水水位上升了7.35 m,上升高度占总上升高度的48.62%;拱墙二衬期间,地下水水位继续上升,期间地下水水位上升了5.44 m,上升高度占总上升高度的35.96%。
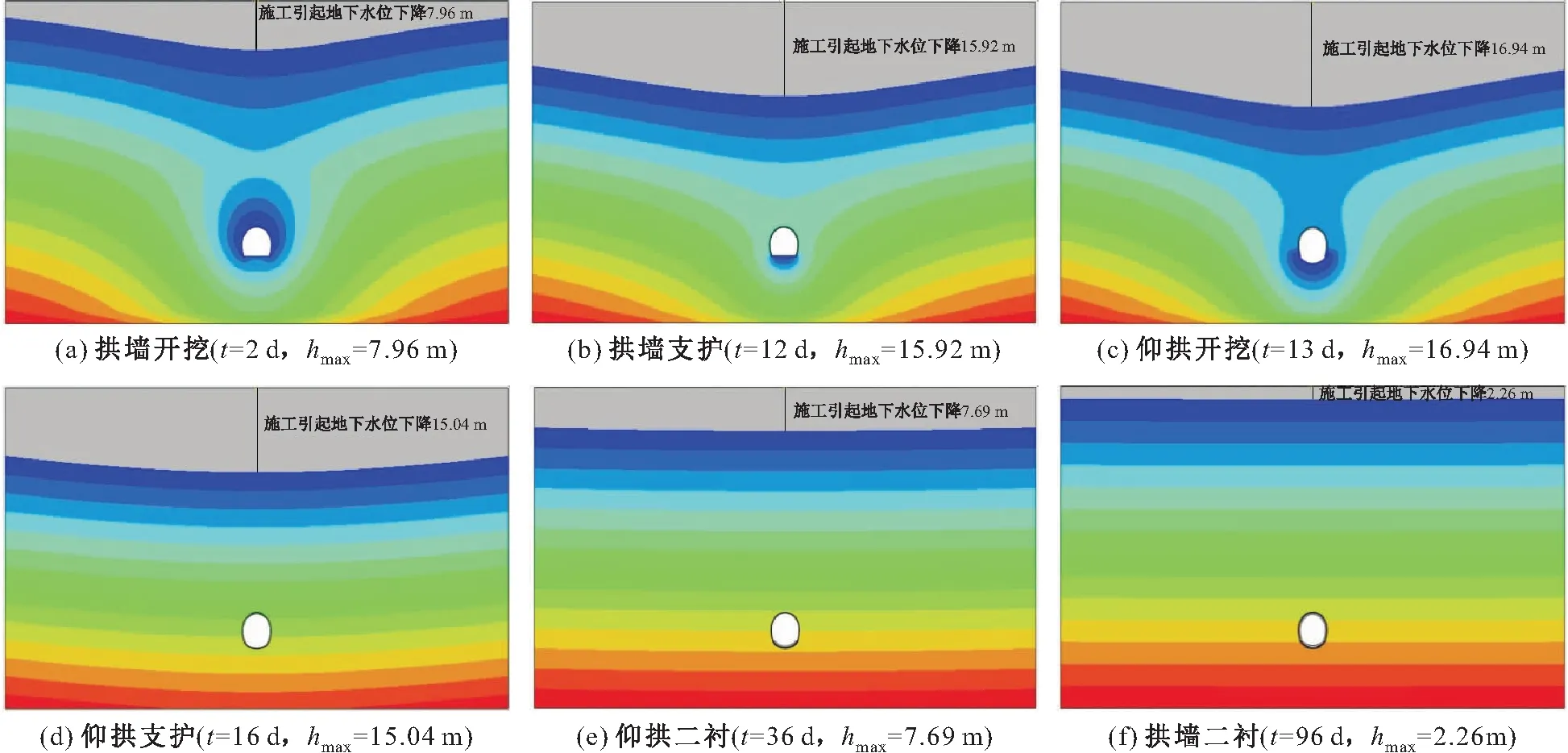
图5 风化花岗岩隧道矿山法施工不同阶段地下水水位分布图Fig.5 Distribution diagram of groundwater level in the weathered granite tunnel in different stages of mining method construction
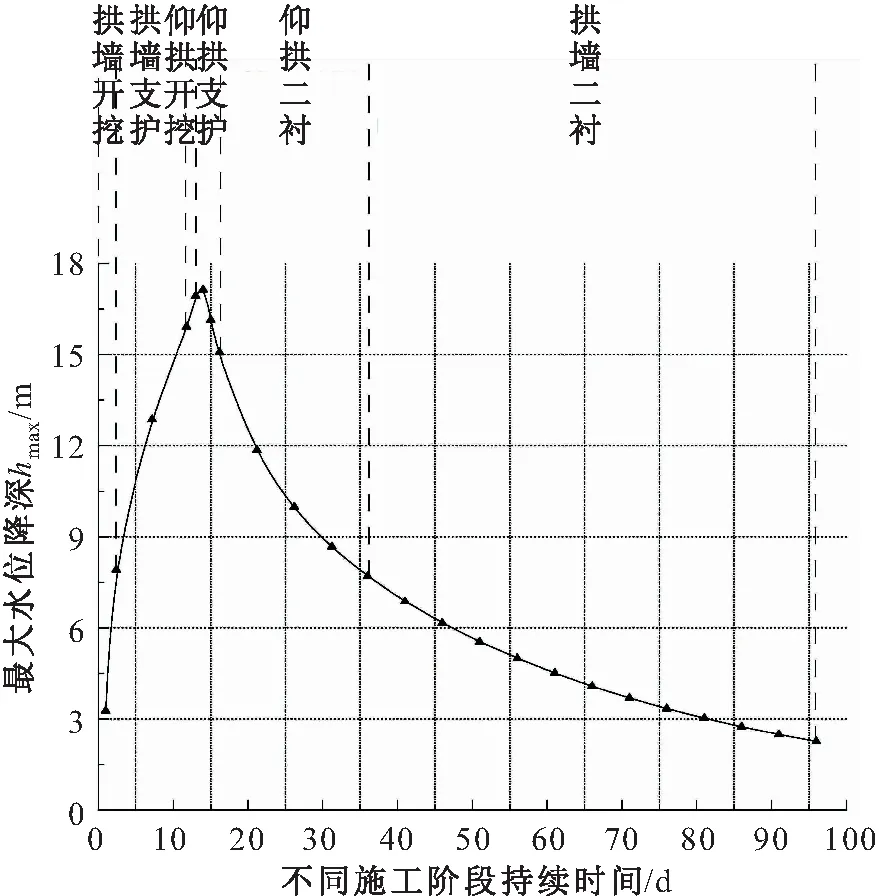
图6 风化花岗岩隧道矿山法施工不同阶段最大水位 降深随施工进程的变化曲线Fig.6 Variation curve of maximum water level drawdown in the weathered granite tunnel in different stages of mining method construction with the construction process
综上分析可见,拱墙开挖期间,地下水水位降低速度最快;拱墙支护期间,地下水水位降低幅度最大;仰拱支护期间,地下水水位开始恢复,地下水水位恢复速度最快;二次衬砌施作期间,地下水水位恢复速度减缓,地下水水位恢复幅度增加;仰拱二衬期间,地下水水位上升幅度最大;整个隧道施工完毕一段时间之后,地下水水位保持稳定,地下水水位较初始情况降低了2.26 m。
3 不同防水结构下流固耦合特征分析
3.1 计算模型
本文采用ABAQUS有限元数值模拟软件在风化花岗岩隧道YDK26+930断面处进行了不同防水结构下地下水渗流场模拟,并结合岩土层参数(见表1)建立二维有限元模型。计算模型中隧道断面采用Ⅲ级围岩复合式衬砌标准断面(见图2),隧道埋深为130 m,地下水补给充足,在地表以下15 m处地下水水位线始终保持不变。数值模拟过程中,通过设置在拱脚处的排水孔来实现控制性全包防水结构的模拟[10],在控制性全包防水结构中排水孔以外的部分不透水。将衬砌内边界水头设为0,保证地下水自由通过隧道内表面,建立了不同防水结构下流固耦合特征分析模型,见图7。
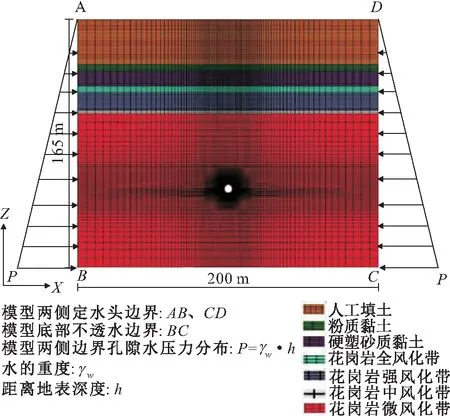
图7 不同防水结构下流固耦合特征分析模型Fig.7 Fluid-solid coupling analysis model under different waterproof structure
3.2 计算参数与边界条件
流固耦合数值模型中放置与2.3节相同的位移和渗流边界,围岩使用Mohr-Coulomb本构模型,初期支护和二次衬砌使用弹性本构模型。模型注浆圈半径为2 m,注浆圈渗透系数为2.16×10-2m/d;通过在计算模型中设置排水孔的方式模拟实际排水管,模型中排水孔设置在衬砌结构中,与二次衬砌材料参数相同,但与二次衬砌材料渗透系数不同。在计算模型中将排水孔孔隙水压力设为0,排水孔渗透系数通过流量相等原则确定。计算模型中排水孔渗透系数的计算公式如下:
(3)
式中:K1为隧道中实际排水管渗透系数,根据实际排水管流量计算出K1为20 cm/s;D为实际排水管直径,为10 cm;L为实际排水管纵向间距,为10 m;d为计算模型中的排水孔宽度,为30 cm[11-12]。
根据公式(2)计算出数值计算模型中排水孔渗透系数K2为45.2 m/d,风化花岗岩隧道YDK26+930断面模型计算参数见表2。
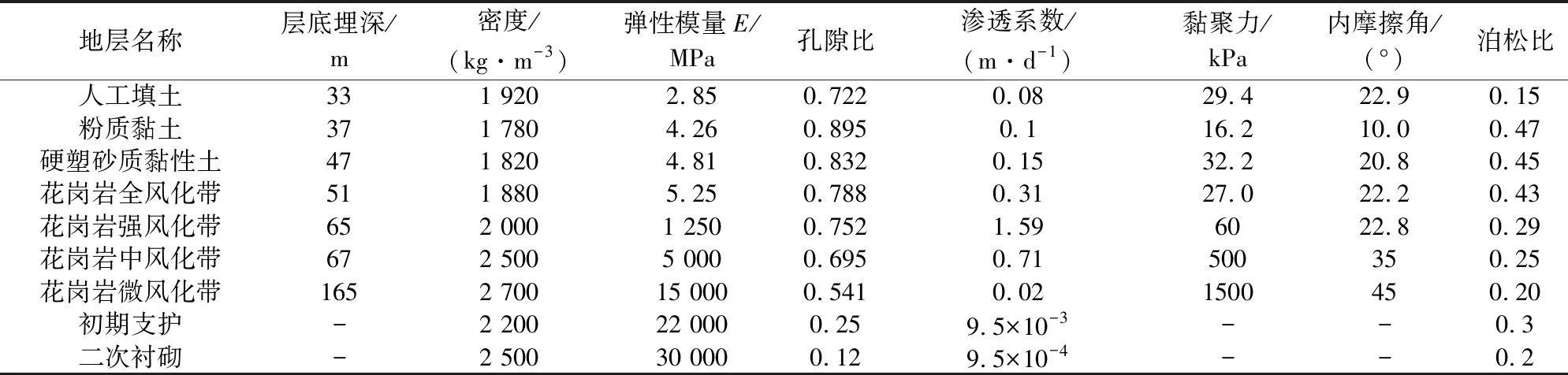
表2 风化花岗岩隧道YDK26+930断面模型计算参数表Table 2 Table of calculation parameters of YDK26+930 section model for the weathered granite tunnel
3.3 不同防水结构下流固耦合特征分析
3.3.1 控制性全包防水结构下流固耦合特征分析
控制性全包防水结构下风化花岗岩隧道YDK26+930断面处二次衬砌背后孔隙水压力分布云图,见图8。
由图8可见,由于防水板的全断面铺设,隧道断面处二次衬砌上几乎没有孔隙水压力分布;靠近仰拱部分,孔隙水压力较小;二次衬砌背后孔隙水压力最大值为0.64 MPa,位于拱顶,最小值为-0.98 Pa,位于二次衬砌与初期支护接触面拱脚排水孔处。
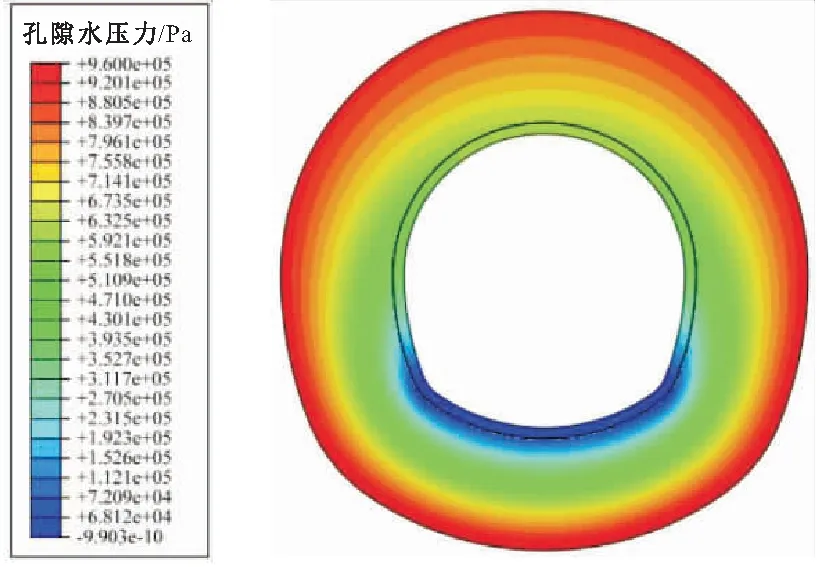
图8 控制性全包防水结构下风化花岗岩隧道YDK26+ 930断面处二次衬砌背后孔隙水压力分布云图Fig.8 Cloud map of the pore water pressure in the YDK26+930 section behind two liners of the weathered granite tunnel under the controlling fully wrapped waterproof structure
由此可见,控制性全包防水结构下风化花岗岩隧道YDK26+930断面处二次衬砌背后孔隙水压力最大值基本位于初期支护与二次衬砌接触面的拱肩以上部分,其最小值基本位于拱脚排水孔处,拱腰以上部分孔隙水压力平均值较大。
3.3.2 全包防水结构下流固耦合特征分析
全包防水结构下风化花岗岩隧道YDK26+930断面处二次衬砌背后孔隙水压力分布云图,见图9。
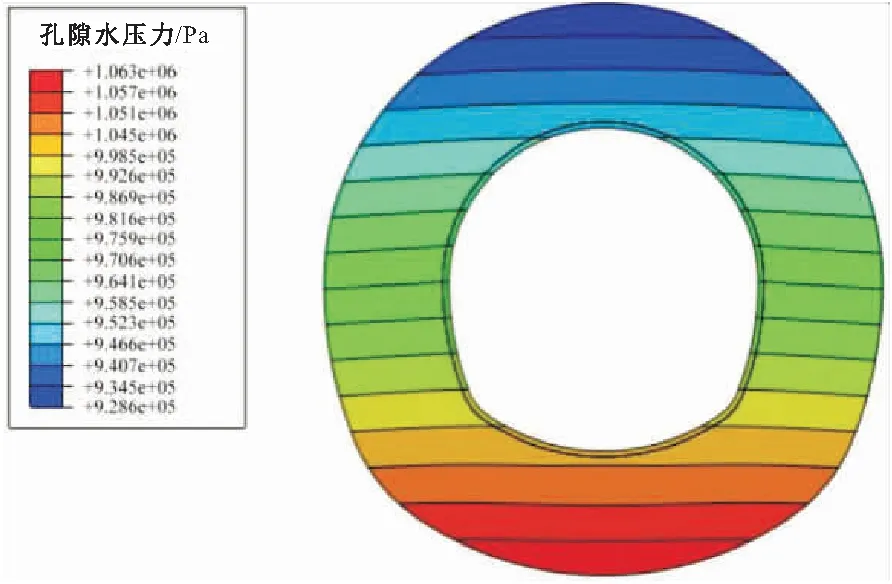
图9 全包防水结构下风化花岗岩隧道YDK26+ 930断面处二次衬砌背后孔隙水压力分布云图Fig.9 Cloud map of the pore water pressure in the YDK26+930 section behind two liners of the weathered granite tunnel under the fully wrapped waterproof structure
由图9可见,隧道断面二次衬砌背后孔隙水压力与静水压力分布一致,竖直方向呈现梯度变化;二次衬砌背后孔隙水压力最大值均位于拱底处,其最小值均位于拱顶处,二次衬砌周围孔隙水压力等值线大致为水平直线,与隧道断面处地层的初始孔隙水压分布基本一致。
3.3.3 模拟结果与现场监测结果的对比分析
为了揭示地下水对二次衬砌的荷载作用,通过埋设在防水板与二次衬砌之间的土压力盒来监测二次衬砌外圈的荷载[13]。二次衬砌附加荷载现场数据采集见图10,风化花岗岩隧道YDK26+930断面

图10 二次衬砌附加荷载现场数据采集Fig.10 Field data acquisition with the load on secondary lining
处二次衬砌荷载时态曲线见图11。
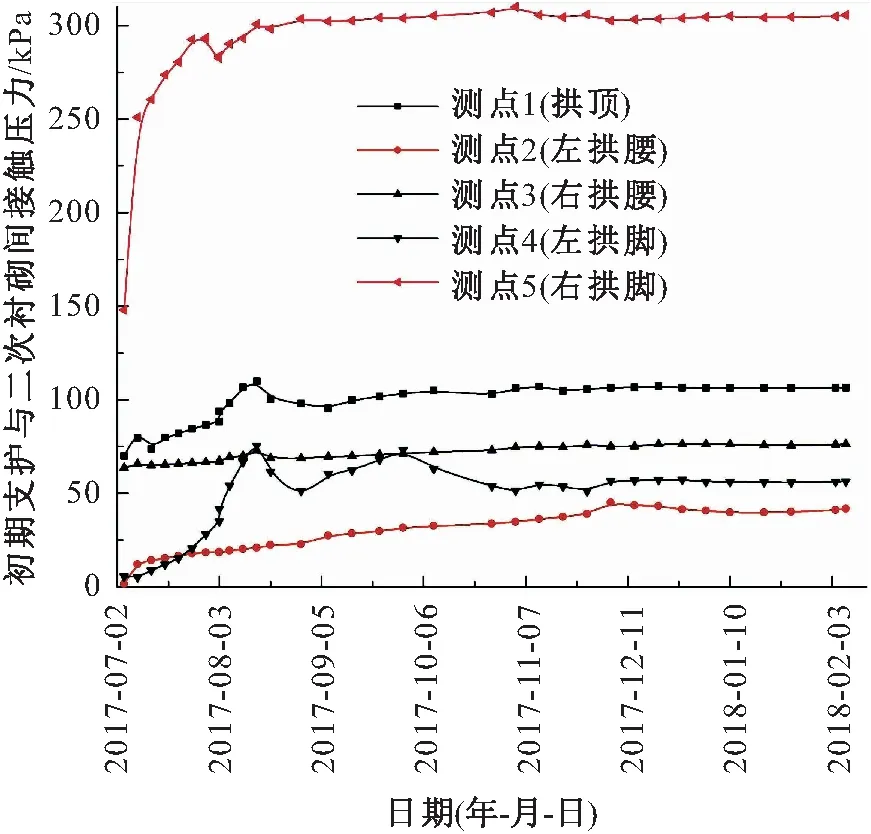
图11 风化花岗岩隧道YDK26+930断面处二次衬砌 荷载时态曲线Fig.11 Time series of the load on secondary lining in YDK26+930 section of the weathered granite tunnel
由图11可见,隧道断面处二次衬砌荷载主要集中于拱顶,拱顶荷载较大,拱脚荷载较小,隧道上部荷载平均值较大。
4 考虑地下水环境变化的防水控制措施
4.1 二次衬砌背后孔隙水压力变化特征
隧址区场地地下水受地形的影响,地下水埋深变化大,地下水水位的变化与地下水赋存、补给和排泄的关系密切,并受季节变化的影响,地下水水位年变化幅度在5 m以内。隧道防水控制措施的选择需要考虑地下水环境的变化,因此本文根据场地地下水水位变化幅度,在不同初始地下水水位埋深条件下模拟不同防水结构对地下水渗流场的影响,研究二次衬砌上孔隙水压力的变化情况,并根据隧道断面特征位置处的孔隙水压力的变化情况,在特征断面处选择合适的防水控制措施。
在流固耦合过程中,地下水补给充足,初始地下水水位保持不变,设定初始地下水水位在原先基础上下浮动6 m,隧道YDK26+930断面处初始地下水水位分别为地表以下9 m、12 m、15 m、18 m、21 m。分别取隧道拱顶、拱腰、拱脚、拱底5个特殊位置为观测点,观测不同防水结构下特殊点的孔隙水压力。不同防水结构下风化花岗岩隧道YDK26+930断面处二次衬砌背后孔隙水压力的数值模拟结果见表3。

表3 不同防水结构下风化花岗岩隧道YDK26+930断面处二次衬砌背后孔隙水压力数值模拟结果Table 3 Numerical simulation results of pore water pressure in the YDK26+930 section behind two liners of the weathered granite tunnel under different waterproofing structures
由表3可知,初始地下水埋深不同时,隧道断面处二次衬砌背后孔隙水压力有着明显的差别,初始地下水水位距离地表越近,二次衬砌背后孔隙水压力差异越明显;通过比较不同防水结构下隧道断面处二次衬砌背后孔隙水压力的变化情况发现,隧道下部结构对防水结构的变化更敏感,仰拱和拱腰处孔隙水压力受防水结构变化的影响较小;全包防水结构下,地下水向隧道下部断面渗流,拱顶处的孔隙水压力最小;控制性全包防水结构下,拱脚处的孔隙水压力最小;初始地下水水位到隧道拱顶处的地下水头越高,不同防水结构下隧道下部结构孔隙水压力分布的差异越大,控制性全包防水结构对孔隙水压力的折减效果越明显。
4.2 防水控制措施
为了直观地表现风化花岗岩隧道各个断面在不同初始地下水水位埋深条件下孔隙水压力的折减效果,定义孔隙水压力折减系数为控制性全包防水结构下孔隙水压力与全包防水结构下孔隙水压力的比值。
经计算,风化花岗岩隧道YDK26+930断面处采用控制性全包防水结构时,拱顶处孔隙水压力折减系数平均值在0.65左右,拱腰处孔隙水压力折减系数平均值在0.39左右,拱脚处孔隙水压力折减系数平均值在0.02左右,拱底处孔隙水压力折减系数平均值在0.064左右,说明排水孔的施作对隧道各个部分的孔隙水压力均起到了很好的折减作用,包括一般情况下折减效果不太显著的拱顶位置,且该断面处的孔隙水压力几乎下降50%,表明在隧道YDK26+930断面处采用控制性全包防水结构能够有效地降低二次衬砌上的孔隙水压力,对提高衬砌结构的安全性作用显著。
5 结 论
(1) 本文通过现场监测和基于ABAQUS有限元数值分析方法,对风化花岗岩隧道在矿山法施工条件下地下水渗流特征和不同防水结构下的流固耦合特征进行了数值模拟与分析,综合考虑了隧道围岩的渗流和力学特征,并在代表性断面处提出了合适的防水控制措施。
(2) 全包防水技术在广州地铁隧道矿山法施工中取得了良好的应用效果,有效地避免了实际隧道施工中地下水的渗漏问题,验证了本文研究成果的合理性。
(3) 全包防水技术和与控制性全包防水技术可在地下水控制要求严格的各类隧道施工过程中应用。
