基于单脉冲跟踪技术的高精度二次雷达跟踪算法

周光鲁 徐 静 高 渊 毛梦月 余 苗

0 引言

二次雷达[1-4]是由询问雷达和应答雷达所组成的无线电电子测位和辨认系统。询问雷达发射电磁波，应答雷达（又称雷达信标）接收到询问电磁波后被触发，发射应答电磁波，询问雷达根据接收到的应答电磁而工作，实现识辨和测位。

某型二次雷达主要用于两台或者多台设备的动态精确跟踪定位。对精度和捕获目标效率有较高要求。单脉冲测角技术[5]可满足高精度的测角要求，但是在满足精度的同时，还需要快速的捕获目标。所以在实现上采用了两段式的工作方式。即先使用宽波束快速搜索目标，再使用窄波束在引导角度上通过α- β 滤波器[6]进行多次迭代跟踪。为保证跟踪的精度以及设备工作稳定性，该设备工作周期为1s，时间上分成一次搜索以及若干次连续跟踪。在每个工作周期内均重复进行搜索- 跟踪的过程，当初次捕获目标或者未建立稳定跟踪时，使用搜索角度作为跟踪的引导角度。建立稳定跟踪以后通过α- β 滤波器实现闭环跟踪[7]。此时搜索过程仍然继续以保证跟踪稳定性。

1 简述跟踪模型

用较宽的波束进行跟踪具有效率高，捕获速度快的优点，但是精度较差。而窄波束跟踪具有高精度的特点，但是捕获目标较为困难。结合两者的优缺点，建立了利用宽波束捕获目标，窄波束跟踪目标的跟踪模型。该模型主要分为以下两部分：

（1）宽波束搜索目标。

（2）窄波束跟踪目标。

由宽波束搜索为窄波束跟踪提供引导角度，跟踪稳定后窄波束进入闭环跟踪，同时宽波束也在同步搜索。跟踪和搜索分时工作。一个完整的跟踪周期分为一次宽波束搜索以及若干次窄波束跟踪，见图1。

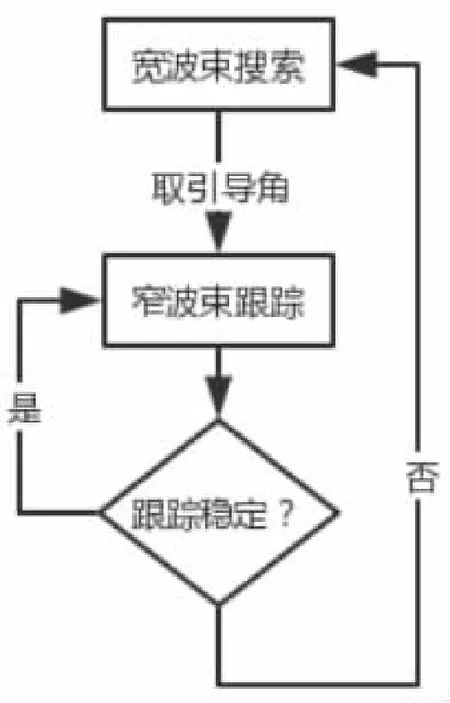
图1

2 宽波束搜索目标

FPGA[8]控制波束在波控最大指向角的范围内进行一次快速扫描，该次扫描以宽波束的波束宽度为步进量，扫描完成后返回具有最大回波强度的波位以及该波位的和差信号，利用该波位的和差信号进行一次角度测量，最终获得宽波束下测量到的目标方位。宽波束搜索目标一个跟踪周期进行一次，见图2。

图2

设阵面的扫描范围为±α°，宽波束波宽为βw，波位数为P，则：

P=（2×α）/βw

扫描完成后，每个波位都会得到一组和差信号。利用和差信号计算信号强度，并取其中具有最大信号强度的波位号Pmax（0≤Pmax≤P），设目标所在方位为 A'，则：

A'=Pmax×βw

该角度A'为目标所在的大致方位，需要利用该波位Pmax所对应的和差信号，进行一次单脉冲测角，计算出误差角Ew。其中：

AW=EW+A'

最终得到的角度AW即为宽波束引导角。该过程每个测量周期进行一次，当捕获目标或者目标丢失时，引导窄波束进行跟踪。

3 窄波束跟踪目标

3.1 单脉冲测角

当初次捕获或者目标丢失时，使用宽波束测量到的目标方位作为窄波束跟踪的引导角度进行引导跟踪。当窄波束跟踪接收到的和差信号满足跟踪稳定门限后，转为闭环跟踪，见图3。窄波束跟踪稳定时不使用引导角度。

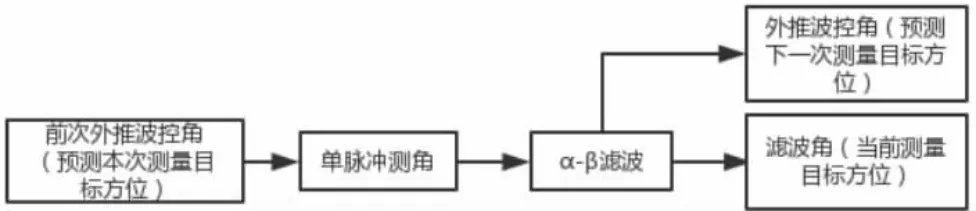
图3

初次捕获目标或者目标丢失时，将波束指向引导角度AW，并利用在方位AW所获取到的和差信号进行一次单脉冲测角[9]，计算出当前的误差角En，则有：

An=Aw+En/cos（Aw）

其中An为该次窄波束测量得到的目标方位。

3.2 A-β 滤波

A-β 滤波器适用于加速度较小的运动目标跟踪，将测量到的目标方位、距离进行滤波，可以平滑噪声带来的测量误差，同时可以预测下一次测量时目标所在方位，即滤波外推。该设备采用RTT 算法[10]进行距离测量，原理如下：

两台设备均采用高精度铷钟产生一个1pps，在采用同样的通信机制下进行信号收发（该通信方式是把1 秒划分为若干等间隔的时间段，采用一定的规则在指定时间段内进行通信），最终可以实现两台设备的时间同步[11]。

当两台设备完成时间同步后，接收方从该信号中解调出信号发出时刻的时戳T1，根据本地接收到信号的时戳T2，信号在机器内部传输的时延T3，以及电磁波在空气中传播的速度V，可由下列公式计算出两台设备间的距离Dn。

Dn=（T2- T1- T3×2）×V

随后对测角值An以及测距值Dn进行α-β 滤波。由于该方位和距离信息属于极坐标系，而极坐标系不是稳定的坐标系，在极坐标系下滤波会造成目标方位抖动。所以为得到稳定的目标距离、方位，需要将极坐标系转换为稳定直角坐标系[12]，在直角坐标系下进行滤波外推处理[9]，转换公式如下：

X=Dn×cos（P）×sin（An）

Y=Dn×cos（P）×cos（An）

Z=Dn×sin（An）

其中P 为俯仰角，由于当前设备均在水平方向上工作，故可认为俯仰角为0。X，Y，Z 分别为直角坐标系下目标所在方位。随后经过α-β 滤波器进行滤波外推，最终输出为：

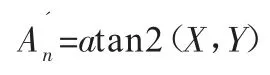
4 实验结果

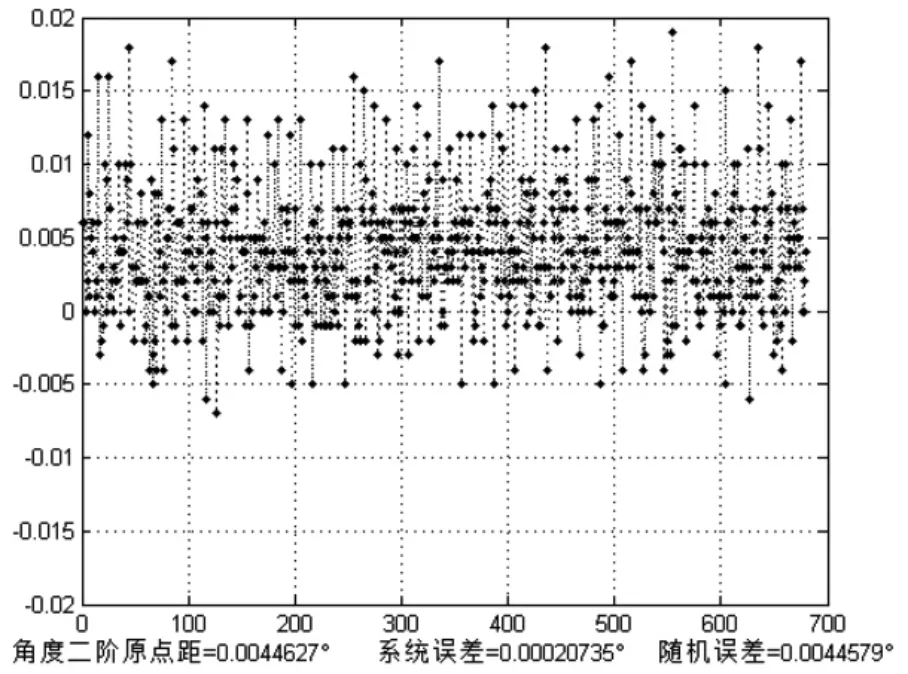
图4

图5

实验结果如图4、图5 所示。其中图4 为滤波前的测量角度，图5 为滤波后的输出角度，最终的角度跟踪精度以及跟踪的稳定性满足系统的设计要求。

以上结果表明本文提出的基于单脉冲跟踪技术的高精度二次雷达跟踪算法是成功的，能实现精确跟踪的功能。