小学数学结构化教学思维的建构策略
2020-08-13周凤花
周凤花

【摘要】文章在结构化思维教学方式的主导与建模的基础上,从关注单元知识结构化设计,关注阶段性知识结构化设计,关注教材重组结构化设计,关注阶段性复习中教学过程的设计四个方面入手,对实现结构化教学思维的构建提出了具有建设性的建议。
【关键词】小学数学;结构化教学思维;建构策略
【基金项目】本文系2018年福建省中青年教师教育科研项目(基础教育研究专项)课题“构建思理相生小学数学课堂的实践研究”中期研究成果,课题立项批准号:JZ180228。
通常而言,结构化教学思维的构建在培养学生思维品质方面发挥了重要作用:一方面,有利于激发学生学习的积极性和主动性,培养学生自主学习能力和自主探究能力;另一方面,有利于培养独立思考的意识,为促进学生的智力发育打下坚实的基础。因此,如何科学构建结构化教学思维是教师在小学数学教学过程中必须思考和解决的问题。
一、关注单元知识结构化设计
首先,教师要树立系统、整体的教学观念,在新课开始之前,要做好对单元知识的结构化设计,通过采用构建横向架构的方式,在教学过程中渗透和融入相关知识点,从而提高学生的学习效率和效果。
例如,复习“多边形面积”相关知识时,教师为学生布置一道练习题:如图1左所示,求解阴影部分的面积。
全班几乎所有学生都采用“梯形面积与三角形面积之差”的方式进行求解。教师在这道练习题的基础上,去掉了一个已知条件,即“梯形的底边长”,要求学生求出阴影部分的面积。此时,学生有点无计可施,不知道如何解答。如果教师利用假设法讲解这道练习题,显然不符合教学的目标和要求[1]。因此,教师利用三角形面积相关推导思想,以常规解题思路为起点,设计出以下解题步骤,帮助学生进行引导和探究,将会取得意想不到的教学效果。
第一,分别画出长方形、平行四边形,然后分别沿着两个图形的对角线将其分成大小相同的两个三角形,并探究出三角形与长方形、平行四边形两个之间的关系,即“等底等高”的关系。由此得出一个结论:三角形的面积是等底等高长方形或者平行四边形面积的一半。
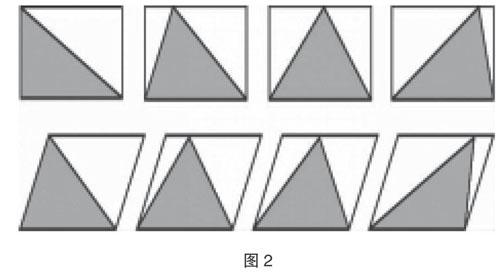
第二,如图2所示,沿着长方形或者平行四边形的底边,对三角形的某一个顶点进行移动,可以得到不同形状的三角形,试问所有不同形状的三角形面积是否均为长方形或者平行四边形面积的一半?如果是,请说出理由。
第三,进入拓展环节。在两个面积和形状都一样的长方形或者平行四边形中,找出其中面积最大的三角形。
第四,进入推理环节[2]。将长方形分割成两个不同形状的三角形,分析两个三角形的面积之和与长方形面积之间的关系,如果分割成三个或四个三角形又有什么关系?
第五,进入延伸环节。有了上面的知识储备后,同学们对如何将两个三角形面积转化为一个三角形面积有了一个新的认识和体会。此时,为学生设计以下练习题:“长方形的长和宽分别为25cm和10cm,试计算出阴影面积。”学生在解答这类题目时就会轻而易举、迎刃而解。然后回到最开始的练习题,利用以上规律,将阴影部分转化为一个三角形进行求解,
由此可见,在日常的数学教学过程中,教师如果能以数学的本质为起点,看重数学知识点的系统性和整体性,引导学生寻找并理解各个知识点之间的内在联系和本质规律,使学生以小见大,科学归纳和整合各个课时知识点之间的联系,就能为更好地培养学生的结构化数学思维创造良好的条件。
二、关注阶段性知识结构化设计
为了进一步培养学生的数学结构化思维,教师在日常教学中要重视对阶段性知识结构的科学设计,引导学生找出知识本源与学习本源之间的异同点,以达到培养学生迁移抽象知识的能力。
例如在讲解“分数的意义”相关知识时,部分学生在应用分数意义的过程中经常出现对不同类型分数的混用问题,例如数量倍数比关系的分数与具体数量分数之间的混用。为了解决这一问题,教师可以为学生详细讲解“五分之三块”的两种含义:第一种含义为一块饼的五分之三;第二种含义为三块饼的五分之一。利用除法运算法则可以实现对分数意义的进一步拓展。拓展后分数的意义既表示整体与部分的关系,又表示求解的每份数(当求解的每份数不满1时用分数表示)。
由此可见,教师在实际教学过程中,要引导学生在联系旧知识的基础上学习新知识,通过找出新旧知识之间的联系,使学生以整体性的思维将分数与整数进行有效联系,以达到深入认识和理解“分数意义”的目的,为后期轻而易举地解答复杂的分数应用题打下坚实的基础。
三、关注教材重组结构化设计
首先,要科学合理地重组和整合教材内容,对数学知识结构进行整体性的把握和系统性的讲解,以设计出符合学生认知特征和学习能力的教学活动,使得学生对所学知识点有一个深入的拓展和延伸,不断训练和提高自身的数学结构化思维,从而提高利用数学知识解决实际生活问题的能力,让学生体会到数学这门学科的应用价值。
例如教师在讲解“简易方程”相关知识时,为了培养学生的创新思维和数学结构化思维,要避免让学生使用传统的四则运算法则对简易方程进行求解,而是让学生利用等式性质对简易方程进行求解。为了实现这一教学目标,教师首先要重视对教学等式性质的讲解,让学生在理解和应用等式性质的基础上,完成对简易方程的快速求解。但是在这个过程中,学生难免会遇到形如“c-x=d”的方程,此时,学生可能会无计可施,不好求解。在这样的情况下,教师要为学生收集和整理含有字母式子的相关练习题,对学生进行专项训练,不断地提高学生恒等变形的能力,从而培养学生熟练应用等式性质求解简易方程的能力,进而加深对“同等变形”这一数学思想的认识和理解。
同时,为了拓宽学生的知识面,提高学生利用不同知识求解简易方程的能力,教师还要为学生讲解利用四则混合运算求解简易方程的过程,让学生认识求解方程的两种方法是相互统一的,而非相互矛盾。例如“甲三角形的面积比乙三角形面积多6cm2,试求解CE的长度”,此时学生就可以运用等式性质对这道题进行求解,求解过程如下:
首先根据题中的条件,列出相应的等式“甲三角形面积-乙三角形面积=6”;然后利用等式性质,在等号的两边同时加上丙梯形的面积;最后将等式转化为“正方形面积-三角形面积=6”,从而快速求解出三角形的面积,进而求出CE的长度。
通过引导学生求解这种类型的练习题,学生对等式性质的应用有了更深入的认识和理解,为培养学生的数学结构化思维提供了有力的保障。
由此可见,教师可以通过关注教材重组结构化设计,引导学生从整体性的角度对知识内部规律进行系统把握。这样一来,不仅有效突破了原有课时不足的局限和束缚,而且能充分理解和尊重学生的主体地位,在科学设计教学内容的基础上,让学生利用原有的认知结构认识和理解新知识,从而发展学生的数学结构化思维。
四、關注阶段性复习中教学过程的设计
教师在日常教学中,要根据学生的学习情况和认知能力,在充分考虑学生思维水平差异性的基础上,以培养学生数学结构化思维为目标,实现对每个单元的复习阶段的科学设计,让学生在实际学习的过程中,将自己已掌握的知识进行重组,训练利用数学结构化思维深入思考和理解题意的能力,从而提高学生对所学知识举一反三和融会贯通的能力。
五、结语
综上所述,为了促进学生智力发展,提高学生的独立思维能力,教师在构建结构化教学思维的过程中,除了要做好以上四个方面,还要树立与时俱进的教学观念,不断改革和创新结构化教学思维构建方法,以设计出新颖有趣的数学教学活动,不断激发学生的学习兴趣,提高学生的智力水平,使学生的思维品质得到全面培养。
【参考文献】
孔祥林.小学生数学思维结构化培养策略初探[J].小学教学参考,2019(05):74.
徐海明.小学数学结构化教学的实践与思考[J].当代家庭教育,2019(35).
