物理题“圆”来可以这样解
2020-08-13江苏陈宏奎
◇ 江苏 陈宏奎
《普通高中物理课程标准(2017年版)》明确指出,高中物理课程应在义务教育的基础上,进一步促进学生物理学科核心素养的养成和发展.通过高中物理课程的学习,学生应具有建构模型的意识和能力;能运用科学思维方法,从定性和定量两个方面对相关问题进行科学推理、找出规律、形成结论.在日常教学过程中,教师应有意识地强化物理问题的辅助线构建,提升学生科学思维能力.从发展学生物理学科核心素养的角度看,培养这种意识是必要的.
辅助线不仅仅局限于作直线,还包括作圆.“圆”是一个完美的图形,高中生基本上对圆知识做到了深入理解,一旦解题时涉及或符合建圆条件,构建辅助圆往往能获得事半功倍的效果.下面结合实例,谈谈如何突破物理问题中的圆辅助线思维.
1 从矢量方向可变的角度切入,构建辅助圆
例1已知力F的一个分力F1与F成30°角,大小未知,另一分力F2的大小为,方向未知.则F1大小可能有几种解( ).
A.无解 B.唯一解
C.两种解 D.不能确定
分析学生都知道用三角形定则(或平行四边形定则)来解决力的合成与分解问题,但本题容易形成漏解.考虑到分力F2大小确定而方向未知的情况,从矢量方向可变的角度切入,可知把所有可能满足条件的F2矢量一端连起来应该正好构成一个圆,一旦想到和画出这条辅助线,即构建辅助圆(如图1),就能看出符合要求的有两种解,问题得以完美解决.
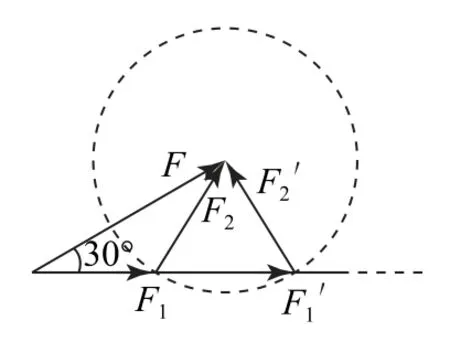
图1
2 从圆周角定理角度切入,构建辅助圆
例2如图2所示,重力为mg的物体用两根绳子OA、OB悬挂,开始时绳OA水平,现将两绳同时顺时针缓慢转过90°,始终保持α角大小不变且物体始终静止,绳OA的拉力为FT1,绳OB的拉力为FT2,则在此旋转过程中不可能发生的是( ).
A.FT1先减小后增大
B.FT1先增大后减小
C.FT2逐渐减小
D.FT2最终变为零
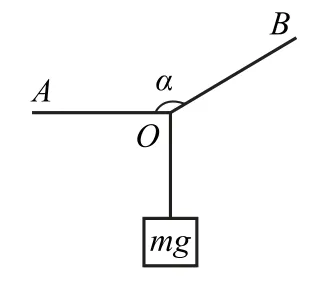
图2
分析分析结点O受力,总有三力合力为零,始终构成一个首尾顺次相连的封闭三角形.注意到矢量三角形一条边固定,即重力大小方向不变,相当于一条弦固定,而两绳同时顺时针缓慢转动变化过程中,矢量三角形另外两条边所夹角度始终保持大小不变,可以由圆周角定理及其推论(一条弦或弧同一侧有相等的圆周角)切入,在初状态的矢量直角三角形的基础上,以表示绳OB的拉力FT2矢量为直径构建辅助圆,再画出后续动态矢量三角形如图3所示,由图看出,FT1先增大后减小,FT2逐渐减小,直到为零,故选项A 正确.
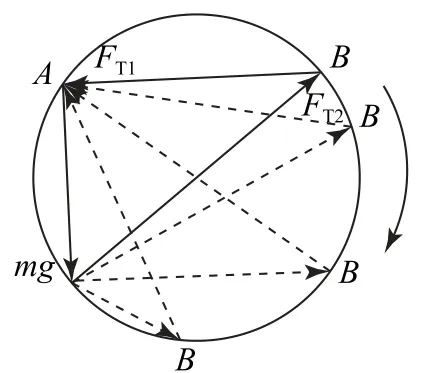
图3
3 从求解微小位移的角度切入,构建辅助圆
例3如图4所示,用一根轻绳拉住一置于水平地面上的物体,绳的另一端通过定滑轮系在一辆小车上,则当小车匀速水平向左拉绳时,物体将做( ).
A.匀速运动
B.减速运动
C.加速运动
D.不能确定
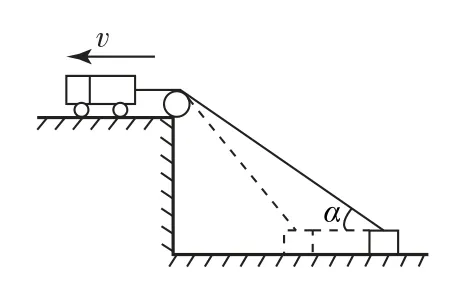
图4
分析本题考查连接体速度关系,即绳(轻杆)两端连接的物体在沿绳(轻杆)方向上的分速度相等.先明确绳两端两物体运动方向.物体的实际运动是水平向左,它的速度可以产生两个效果:一是使定滑轮右侧绳子缩短;二是使定滑轮右侧绳子与竖直方向的夹角减小.所以将物体速度沿绳方向和垂直绳方向进行正交分解,设小车匀速向左拉绳速度为v,得物体速度而α逐渐增大,则物体速度v1逐渐增大,选项C正确.
连接体速度关系是高中物理知识难点,不少学生掌握不好,不清楚知识本质,导致解题错误.其实,根据速度等于位移除以时间,借助微元思想,依然可以有效求解.在极短时间t内,要找沿绳方向绳子缩短的速度(小车匀速向左拉绳速度)和物体向左运动速度之间的关系,只需要找到位移关系即可.从求解微小位移的角度入手,以定滑轮结点O为圆心,以缩短后绳长OB为半径构建圆辅助线如图5,则小车速度而物体速度v1=根据数学知识,在极短时间Δt内,∠COB极小的情况下,△ACB可视为直角三角形,易得sABcosα=sAC,则得出一致结果.
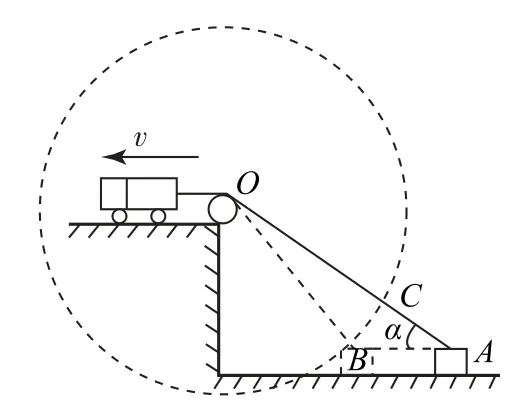
图5
4 从等时圆模型的角度切入,构建辅助圆
例4如图6所示,AB弧是半径为R的1/4圆弧,在AB弧上放置一上表面光滑的木板DB.一质量为m的木块在DB板的上端由静止下滑,然后冲上水平面BC,在BC上滑行L距离后停下(设在B点无能量损失).已知木块m与BC间动摩擦因数为μ,求木块m在DB板上运动过程中重力的平均功率.
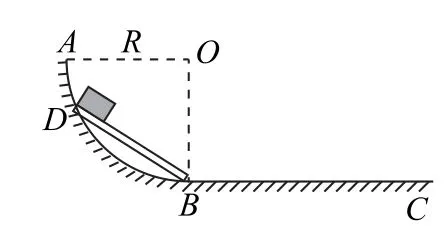
图6
分析本题难点不在于求木块在木板上运动时重力做的功,而在于木块在光滑木板上运动时间的求解.看似题给条件不充分,实则暗藏等时圆模型(附:物体沿位于同一竖直圆上所有光滑弦由静止下滑,到达圆周最低点所用时间相等,这样的竖直圆即简称为“等时圆”).该题立意新颖,出题角度独特,对考生的模型构建、知识迁移、分析综合能力要求较高.
补全半径为R的1/4圆弧形成一个“等时圆”,由“等时圆”结论可知:木块在光滑木板上运动时间等于从圆最高点向下做自由落体运动2R距离到B点所用时间,即,由此问题得以突破.
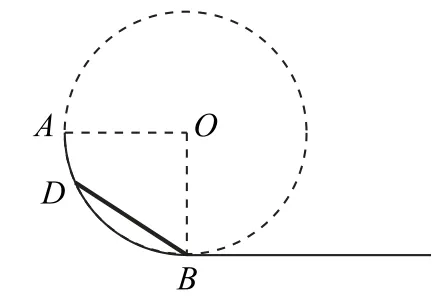
图7
5 从卫星变轨问题的角度切入,构建辅助圆
例5航天飞机在完成对哈勃空间望远镜的维修任务后,在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图8.航天飞机在轨道Ⅱ上经过B的速度与在轨道Ⅰ上经过A的速度相比哪个大?
分析航天飞机运动在轨道Ⅱ上经过B的速度是椭圆轨道近点的速度,大于在轨道Ⅱ上经过A点的速度(远点速度).由变轨知识知轨道Ⅰ上经过A的速度也大于在轨道Ⅱ上经过A点的速度.题给问题貌似无法比较,思路陷入僵局.
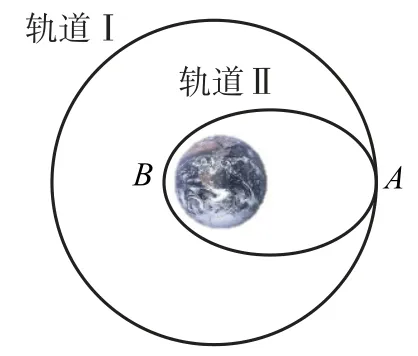
图8
椭圆轨道与圆轨道比较线速度大小肯定要从卫星变轨问题的角度切入,所以过B点构建一与椭圆轨道相切的圆轨道Ⅲ,由变轨知识,即加速离心转高轨推知航天飞机在轨道Ⅱ上经过B的速度大于航天飞机在圆轨道Ⅲ上经过B的速度,由圆周运动知识可知在圆轨道Ⅲ上经过B的速度大于在圆轨道Ⅰ上经过A的速度,则航天飞机在轨道Ⅱ上经过B的速度大于在轨道Ⅰ上经过A的速度.

图9
6 从点电荷等势面的角度切入,构建辅助圆
例6某点电荷的电场线分布如图10所示,同一电场线上有A、B、C三点,且满足距离AB=BC,试比较UAB与UBC的大小关系.
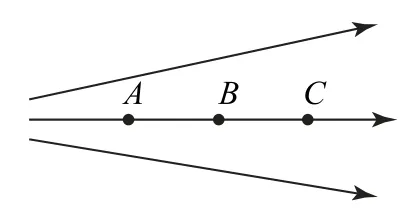
图10
分析由题意判断出点电荷带正电,由点电荷等势面的特征可知等势面为同心球面,且离点电荷越远等势面越稀疏,从点电荷等势面的角度切入,先画出过A点与C点的等势面辅助圆如图11所示,再画A、C两点中间电势的等势面,这有助于加深理解相应知识,解决问题自然也会更迅速.
总之,高考物理改革的总趋势为从知识立意转为能力立意,高中生要将物理知识的学习内化为具备物理学科特性的必备品质和关键能力,养成从题目中提炼核心关键信息并多思考的习惯,训练自己借助辅助线综合分析和解决实际问题的能力.
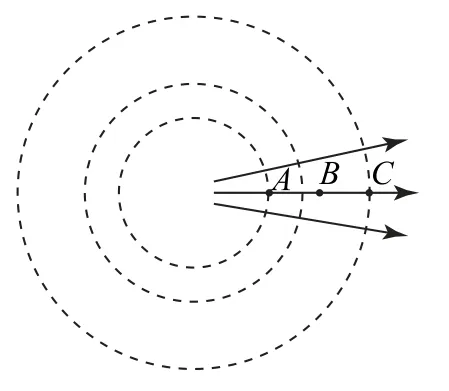
图11
