分离常数法解决高考导数恒成立问题

◇ 福建 韩 旭

导数大题通常是高考数学试卷中的压轴题.《普通高中数学课程标准(2017 年版)》指出导数思想丰富、内涵深刻、应用广泛,对学生的直观想象、逻辑推理、数学抽象和数学运算等核心素养进行了有效考查.总结历年各省市的数学高考题中的导数大题,发现第一问多考查求函数解析式、求函数的切线方程、判断函数单调性、求函数的极值最值等;第二问多考查高阶导数的相关知识、洛必达法则下的导数问题、恒成立问题、根的分布情况、不等式的证明等.

笔者在分析高考题后发现导数中的恒成立问题在所有题型中出现的频率最高,并且该问题常出现在导数大题的第二问中,是拉开学生分数的关键.因此分析和总结恒成立问题的题型和解答方法是十分必要的,本文主要对导数中的恒成立问题展开分析.

1 什么是导数中的恒成立问题

1)题中有明显词语

如“恒成立”“恒有”“总有”“都有”“对任意……有……”“存在……有……”等.

2)和定义域有关的说法

3)和最值有关的说法

如f(x)在[α,β]上最大值为2,用恒成立的角度考虑问题可以转化为f(x)≤2在[α,β]上恒成立.

2 分离常数法解决导数恒成立问题

分离常数法是利用导数求参数范围的首选方法,所谓分离常数是指想要求哪个参数就把哪个参数看成常数放在不等式的一侧,其余量放在不等式的另一侧,再构造新函数h(x),结合题意求解.

2.1 直接求得导函数零点

例1设a∈R,f(x)＝ax3－3x2,若g(x)＝f(x)＋f′(x),x∈[0,2],在x＝0处取得最大值,求a的取值范围.

解析

依题意有g(x)＝ax3－3x2＋3ax2－6x＝ax3＋(3a－3)x2－6x≤0在x∈[0,2]上恒成立,即

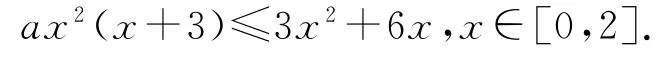
当x＝0时,解得a∈R.当0＜x≤2时,解得a≤,令再求h(x)的最小值即可.

h′(x)＝恒小于0.h(x)在(0,2]上单调递减,则当x＝2时,h(x)有最小值h(2)＝,故.

2.2 无法求出导函数零点

当无法直接求出h′(x)＝0的根,或不能直接判断h′(x)的正负,无法得到h(x)增减性(如当h′(x)是由y＝ax,y＝logax,y＝sinax,y＝ax等函数中至少两类构成时,x的值无法解出)时,我们可以在h(x)的基础上设新的函数t(x),利用t(x)的最值进行解题(实质是求高阶导数).

例2f(x)＝ex－1－x－ax2,当x≥0 时,f(x)≥0恒成立,求a的取值范围.

解析

依题意有ex－1－x－ax2≥0,即ax2≤exx－1.

当x＝0时,解得a∈R.

当x＞0时再求h(x)的最小值即可.

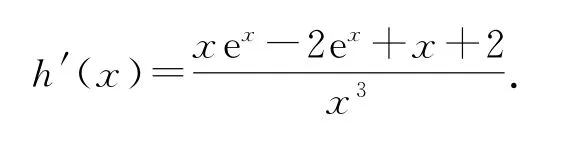
令t(x)＝xex－2ex＋x＋2,t′(x)＝xex－ex＋1.(发现仍无法求出t′(x)＝0的根,故继续求导.)

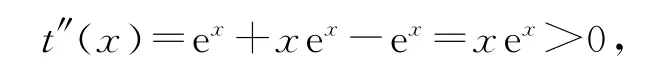
则t′(x)在x＞0上单调递增,故t′(x)＞t′(0)＝0.因此t(x)在x＞0 上单调递增,t(x)＞t(0)＝0.所以h′(x)＞0,h(x)在x＞0 上单调递增,则有h(x)＞h(0).故即.

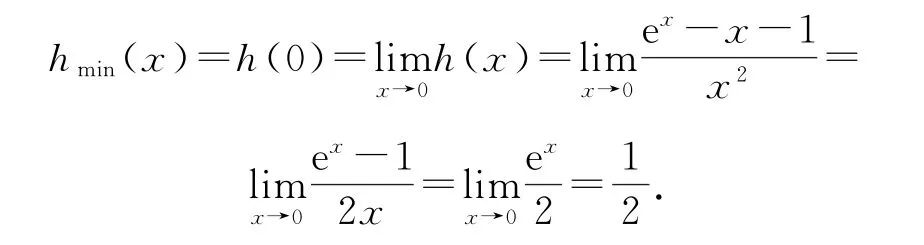
综上所述,a≤.

2.3 区间端点值不为0

若在计算中得到t(x)大于某一正数或t(x)小于某一负数,则可用零点定理进行估根.

[零点定理](介值定理推论)函数f(x)在闭区间[a,b]上连续且有f(a)·f(b)＜0,则∃ξ∈(a,b),使f(ξ)＝0.

例3成立,求整数k的最大值.

解析

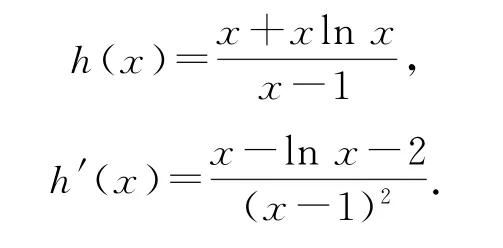
接下来对t(x)＝0估根.因为t(3)＝1－ln3＜0,t(4)＝2－ln4＞0,则存在ξ∈(3,4),使得

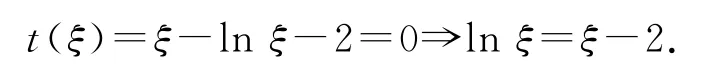
分析其单调性,如表1.

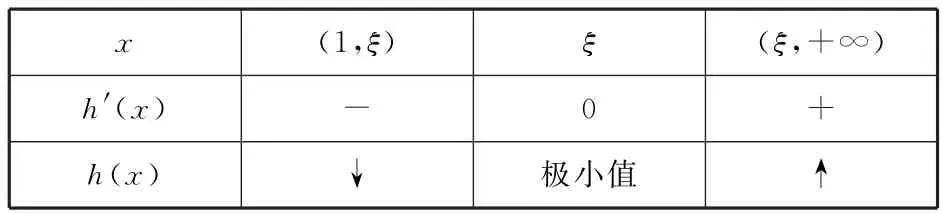
表1

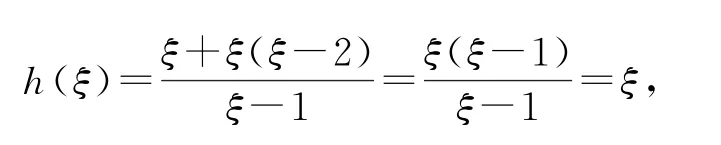
所以k＜ξ.又因为3＜ξ＜4且k∈Z,则kmax＝3.