圆锥曲线中三点共线的坐标度量与常见变形

◇ 山东 李 浩

众所周知,圆锥曲线的问题一般可通过设线与设点进行求解,而椭圆、双曲线内的问题又以设线居多,究其原因,是设点运算的不对称性或代数运算较大导致的.现行的几个版本高中教材中,很少分析三点共线的设点代数表达,人教版《选修2-1》中,也只提到了椭圆及双曲线与直线的相交联立,结合根与系数的关系运算.本文旨在通过以截距定值的弦为例,探究三点共线的坐标度量与常见变形,为读者提供问题求解的思考角度.

1 操作演示

假设A(x1,y1),B(x2,y2)是椭圆(a＞b＞0)上不同的两点,且直线AB经过点M(m,0),则

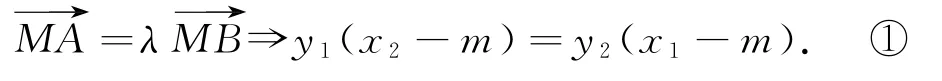
图1

我们单从设点的角度切入分析,不考虑设线联立,利用根与系数的关系,对式①一般可进行如下操作.

操作1平方

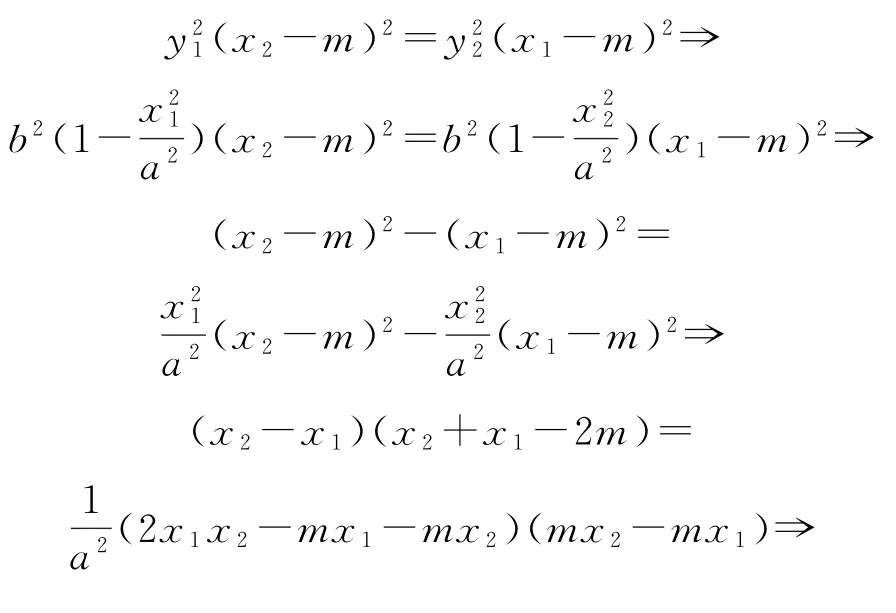
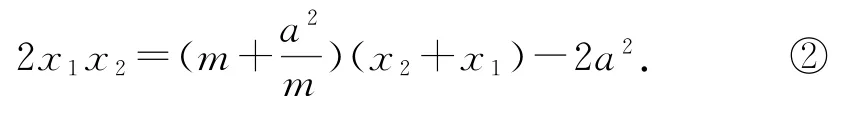
(这是两根和积关系的线性表示.)

分析此操作的目的可以实现共线的三点横坐标之间的互化,以达到“知二求一”的目的,为后续的快速解题提供方便.当然该式的获得也可从根与系数的关系代数运算推得,有兴趣的读者可以自行尝试.

操作2移项对偶构造

分析此操作的目的是可以实现杂交项x1y2和x2y1的代数求解,用两根之和与两根之差来线性表示,结果不仅呈现了对称美,更反映了横坐标与纵坐标之间的内在联系.

操作3等比定理

分析这里若是结合式②,我们还能得到更奇妙的表示,即y1y2能以x2＋x1或x1x2单独线性表示,实现共线三点纵坐标与横坐标之间的线性互化.如：

图2

类比椭圆操作：假设A(x1,y1),B(x2,y2)是抛物线y2＝2px(p＞0)上不同两点,且直线AB经过点T(t,0),则

操作1平方

操作2移项对偶构造

从上述操作中,我们不难发现,设点运算对于共线三点的坐标间的关系描述尤为细致,彼此之间可以实现对称转化,这为我们实际解题提供了新的方法,下面我们来看看上述操作在实际中的应用.

2 实例分析

例若双曲线左、右两支上各有一点A,B,点B在直线上的射影是点B′,若直线AB过右焦点,求证：直线AB′必过定点.

图3

证法1设A(x1,y1),B(x2,y2),由A,B的任意性及曲线的对称性可知,AB′所过的定点必在x轴上,记(x0,0),易得又A,F,B三点共线,y1(x2－2)＝y2(x1－2),由对偶性构造可得

代入x0可得,

证法2设A(x1,y1),B(x2,y2),由A,B的任意性及曲线的对称性可知,AB′所过的定点必在x轴上,记为(x0,0),易得

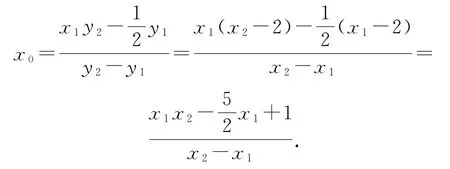
又A,F,B三点共线,y1(x2－2)＝y2(x1－2),平方处理化简,可得

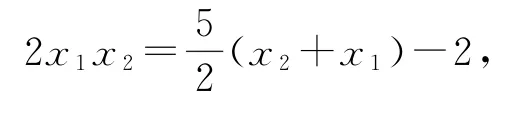
代入x0,可得

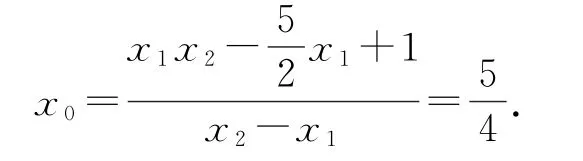
点评

证法1侧重于对形式x1y2的求解,从而想到对偶式的构建.证法2侧重于对未知数x的处理、两根和积关系的转化,两种解法的共同特点都是把原式“非齐次”问题转化为“齐次”处理,2个例题都为我们设点后的坐标代数处理提供了很好的实践机会.

3 结语

本文以截距为定值的弦为例,展现了设点下的三点共线坐标度量与常见变形,分别是平方、移项构造对偶式求解、等比定理,然后利用点在圆锥曲线上,用圆锥曲线方程整体代换的思想,其他直线过定点的情况也可通过坐标平移转化成截距为定值的弦的情况考虑.通过上述案例的分析,我们不难发现,圆锥曲线中的设点代数运算,并没有想象中那么复杂,合理利用结构形式,观察发现需要怎样的变化,应该是设点求解中最重要的.