处理归纳推理问题的几个基本原则

◇ 江苏 姜亚琴

归纳推理是由某一事物的局部特征探究其整体规律的一种思维方式,是由特殊到一般的推理方法.通过归纳提出问题,进而对问题进行分析、求解.在数学中很多重要公式、性质、定理的发现都是通过归纳推理得出的.高考或模拟考试中的归纳推理问题,是考查考生分析问题、解决问题能力以及创新思维的有效载体.本文提出求解归纳推理问题的几个基本原则,供同学们参考.

1 要明确归纳对象的存在条件

例1设数列{an}的通项公式为an＝3n(n∈N*).数列{bm}定义如下：对任意m∈N*,bm是数列{an}中不大于32m的项的个数,则b3＝________;数列{bm}的前m项和Sm＝________.

解析

当m＝1时,32m＝9,由3n≤9,得n≤3,所以b1＝3;当m＝2 时,32m＝34,由3n≤34,得n≤33,所以b2＝33;当m＝3时,32m＝36,由3n≤36,得n≤35,所以b3＝35;

……

依此类推,可得bm＝32m－1,所以数列{bm}是以3为首项,32为公比的等比数列,故

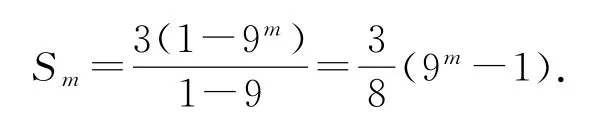
点评

本题归纳的对象存在于新定义的数列中,通过准确理解新定义的概念,探究新定义数列的形式,归纳前几项的规律,明确了新数列的本质,从而使问题顺利获解.

2 要准确应用归纳问题的背景

例2给n个自上而下相连的正方形着黑色或白色,当n≤4时,在所有不同的着色方案中,黑色正方形互不相连的着色方案如图1所示,由此推断,当n＝6时,黑色正方形互不相连的着色方案共有________种,至少有两个黑色正方形相连的着色方案共有_________种(结果用数值表示).

解析

由已知条件,可得当n＝1 时,有2 种着色方案;

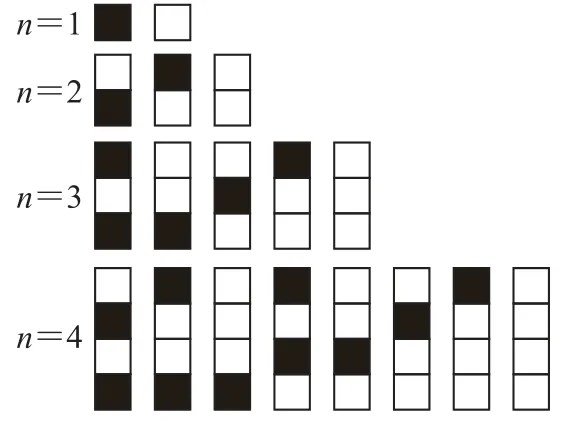
图1

当n＝2时,有3种着色方案;

当n＝3时,有2＋3＝5种着色方案;

当n＝4时,有3＋5＝8种着色方案;

当n＝5时,有5＋8＝13种着色方案;

当n＝6时,有8＋13＝21种着色方案.

因为当n＝6时,每个小正方形有2种着色方案,故共有26＝64种着色方案,黑色正方形互不相连的着色方案有21种,故根据补集法,可得至少有两个黑色正方形相连的着色方案为64－21＝43种.

点评

本题归纳对象的背景源于“斐波那契数列”,即满足F1＝F2＝1,Fn＝Fn－1＋Fn－2(n＝3,4,5,…)的数列{Fn}.本题可设符合题目条件的着色的方案种数为an.

当n≥3时,有两种情况：

1)第1个正方形着白色,则后面的n－1个正方形的着色方案数是an－1;

2)第1个正方形着黑色,则第2 个正方形着白色,后面的n－2个正方形的着色方案数是an－2,所以a1＝2,a2＝3,an＝an－1＋an－2(n＝3,4,5,…),进而得数列{an}的各项依次是2,3,5,8,13,21,….所以n＝6时,共有21种着色方案.

3 要敏锐识别归纳对象隐藏的关系

例3按图2的规律摆放的图形中,“圆点”的个数分别为1,3,6,10,… 将其记为数列{an},在数列{an}中能被5整除的数按从小到大的顺利构成一个新的数列{bn},则

(1)b2020是{an}中的第________项;

(2)b2k－1＝________(用k表示).

图2

解析

通过归纳上述规律猜想

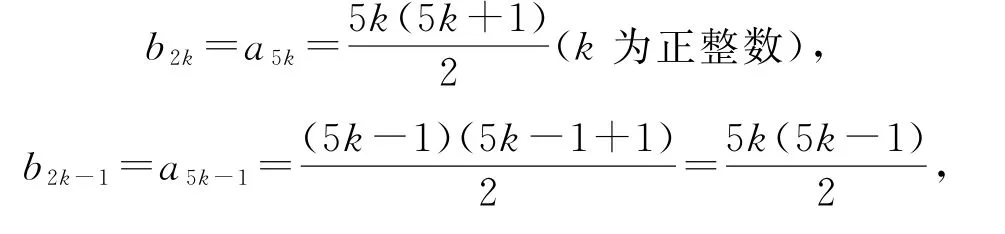
所以b2020＝b2×1010＝a5×1010＝a5050,即b2020是数列{an}中的第5050项.

点评

本题求解中先归纳各图形中“圆点”个数,猜想数列{an}的通项公式,再列举归纳bn与an的关系,从而将隐含的规律一一挖掘出来.

4 要对归纳结论对错进行判断

例4已知数列{an}(an＞0)的前n项和为Sn,且∀n∈N*,有恒成立.

(1)求a1,a2;

(2)猜想{an}的通项公式,并证明.

解析

(1)当n＝1时因为an＞0,所以a1＝1.

当n＝2 时,即a1＋a2＝将a1＝1代入得a2＝2.

(2)当n＝3时,a3＝3,故可猜an＝n.

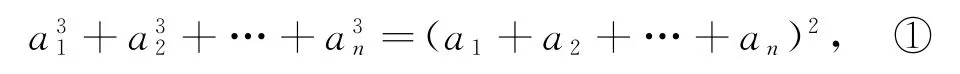
则

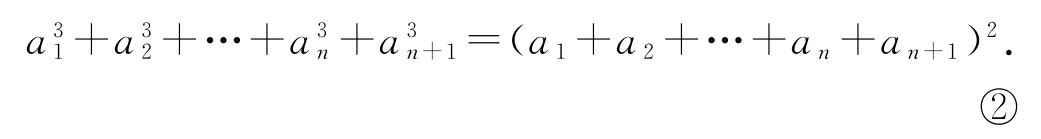
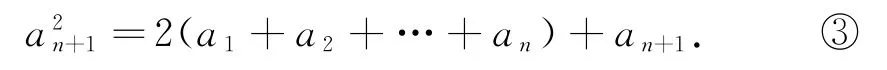
同理

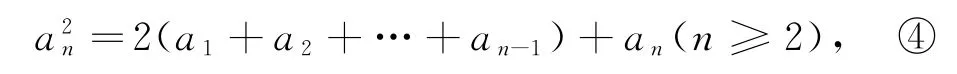
因为a2－a1＝1,即n≥1时均有an＋1－an＝1,故{an}是以1 为首项,1 为公差的等差数列.所以an＝n.

点评

归纳猜想得出的结论正确与否需要进行证明,数学归纳法是一种重要的证明方法.需要注意的是有时归纳推理得出的结论不一定正确,但我们可以通过对不正确的结论进行调整,以期得出更合理的猜想.