基于排队理论的自动化物流仓储系统规划研究
2020-08-13章俊哲李金村
章俊哲,李金村,徐 健,杨 骁,蔡 靖
(1.北京机械工业自动化研究所,北京 100120;2.北自所(北京)科技发展有限公司,北京 100120)
0 引言
国家的立国之本在于制造业,制造业的蓬勃发展意味着国家经济的突飞猛进。在制造业自动化生产的过程中,产生了一些新的问题,比如输送、仓储等。美国的福特汽车公司曾经做出过调查,生产工艺只花费了大概5%的时间,而95%的时间花在了零件的搬运和成品货物的仓储,大大浪费了成本。从中可以看出,越来越多的企业选择自动化物流仓储系统作为企业构成的重要环节[1]。
随着自动化物流仓储系统应用越来越广泛,很多学者开始对其进行研究和优化。薛亚莉通过对遗传算法和模拟退火算法[2]进行改进和融合,优化了立体仓库的货位。刘恺文等人为了合理进行货位的分配,研究了定位存储和随机存储两种入库策略[3]。Banu.Y.Ekren通过穿梭式储存和检索系统[4]对自动化立体库进行设计,克服了由于电商增加而导致的问题,具有更高的处理订单效率。褚东亮等人通过计算机仿真软件Flexsim对某物流企业的自动化立体仓库进行动态建模仿真,研究人员效率、设备利用率是否能达到预期的效果[5]。以往的学者对物流仓储系统中的自动化立体仓库进行了优化,但是对自动化物流仓储系统整体布局和规划分析的较少。
本文应用排队理论对自动化物流仓储系统进行数学模型的抽象研究,推算出评价参数来合理地规划物流设备数量,保证在投入成本最小的情况下得到最优的方案。确定方案以后进行仿真,验证该物流方案。
1 自动化物流仓储系统的排队模型
1.1 系统概述
图1是A厂的自动化物流仓储系统流程图,主要设备包括货架、堆垛机、机器人、输送线等。
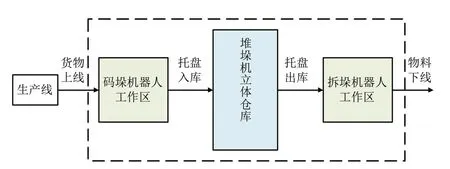
图1 A厂自动化物流仓储系统流程图
机器人进行对货物的码垛和拆垛,每次抓取1件货物。立体仓库中每个巷道均有左右两排货架,具有多层多列,每个货位可存放一个托盘;堆垛机是完成托盘在库内存取,并与输送线交互实现托盘的出入库的设备;输送线的作用是将货物或者托盘在各个环节之间进行传送。
1.2 排队理论概述
排队理论是解决现实中的“服务问题”的一种方法,是一种研究系统由于各种随机因素导致整个系统出现堵塞的现象,从而通过调节一些因素来减少堵塞现象的理论,一般模型如图2所示。排队理论可以通过设定参数,建立模型,来模拟实际情况。再通过计算,得到一些指标参数,优化与分析整个系统。
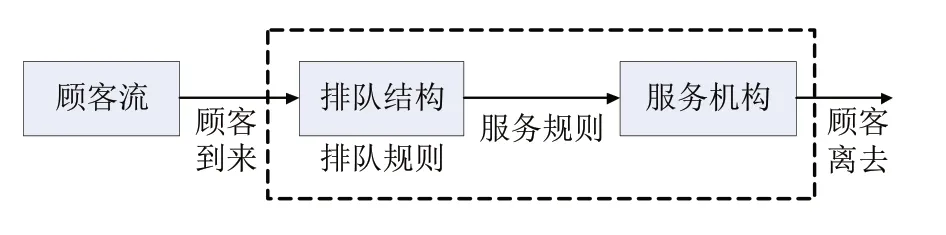
图2 排队模型框图
1.3 排队模型建立
根据排队理论对A厂的物流系统各环节进行建模:
1)入库前,顾客流为单件货物,码垛机器人为服务机构,单件货物通过输送线运送至码垛机器人进行码垛,6件货物码放为一垛,码垛完毕视为服务结束,即顾客离去。
2)入库时,顾客流为托盘,服务机构为堆垛机,堆垛机将托盘存入相应的货位后,视为服务结束。
3)出库时,顾客流为托盘,服务机构为堆垛机,托盘被堆垛机运送至出库端放置完毕后,视为服务结束。
4)出库后,托盘被运送至拆垛机器人,顾客流为托盘,服务机构为拆垛机器人,拆垛机器人进行拆垛,拆垛完成以后,视为服务结束。
结合排队理论,根据A厂的设计参数,对系统做出模型的约束松弛条件:
1)所有的顾客流均服从先到先服务(FCFS)原则:

2)顾客的到达数量无限且相互独立,单个顾客到达服务台的过程服从泊松分布,顾客到达时间间隔服从负指数分布;
3)系统中各服务台的服务时间相互独立,服务台的作业时间服从负指数分布;
4)整个系统不存在等待损失。
根据以上的约束松弛条件可知,系统符合多服务台等待制排队模型。
多服务台等待制排队模型可以分为两类:多队列多服务台等待制排队模型,即s个M/M/1排队模型;单队列多服务台等待制排队模型,即M/M/s排队模型。根据文献[6]可知1个M/M/s系统的工作效率要比s个M/M/1系统的工作效率高,因此要根据M/M/s排队模型对物流仓储系统进行规划。如图3所示,M/M/s模型的顾客都会排成一队,当有服务台处于空闲时,顾客进入服务台进行服务。

图3 单队列多服务台等待制排队模型框图
1.4 系统运行指标
图4是基于多服务台等待制M/M/s排队模型的A厂物流系统流程图。
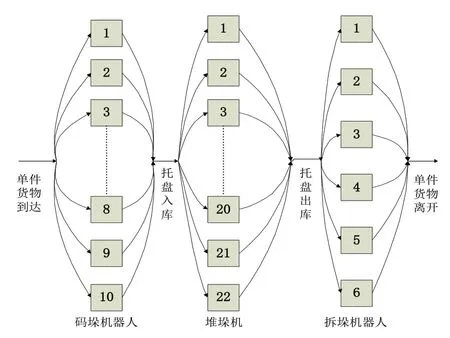
图4 A厂多服务台等待制M/M/s排队模型
设系统各环节的顾客到达过程服从参数为λi的泊松分布,各环节的服务台服务时间服从参数为μi的负指数分布,其中i=1,2,3,4。M/M/s的排队理论模型评价指标的计算方法[7]如下:
1)系统服务强度为:

2)系统中所有服务台都空闲的概率为:
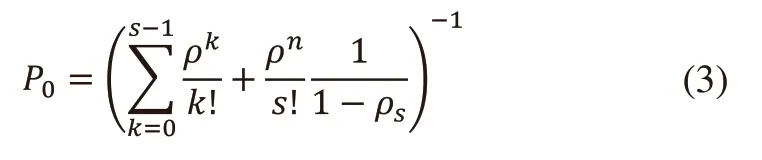
3)平均队长为:
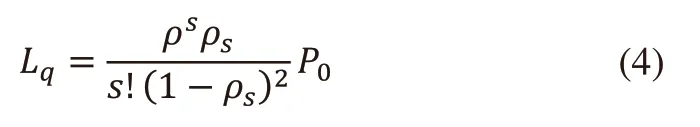
4)平均正在服务窗口:

5)系统队长:

6)货物的平均等待时间:

7)系统内货物必须排队的概率:

8)服务台的运行效率:

2 实例分析
2.1 根据需求计算出入库流量
1)码垛入库系统的流量计算
根据A厂厂商计划,预计到2030年产量最高会达到1520万件,每年工作300天,每天工作16个小时,一个托盘存放6件货物,可以计算出每小时的入库量为3166件/h,即527托盘/h。
2)出库系统的流量计算
通过对零售和电商的出库数据进行处理分析,并考虑企业发展规划,对未来物流中心零售业务的物流需求进行预测,当前规划的日出库目标值为50000件,出库系统每天工作24小时,即347托盘/h。
2.2 各环节排队模型输入参数确定
1)码垛系统
设定码垛机器人的码垛能力μ1为大约10s抓取一件货物,即μ1=60托盘/h;已知系统的入库流量λ1为527托盘/h,即λ1=527托盘/h。根据以上参数,可以得到系统服务强度:ρ1=λ1/μ1=8.78。故码垛机器人的数量需要大于等于9台。
2)入库、出库系统
码垛机器人码放完毕以后,托盘通过输送线运送至堆垛机,执行入库流程。根据出库订单,堆垛机执行出库任务取货,将托盘出库。立体仓库作为系统的中间环节,需要对堆垛机的数量进行优化。
对于单台堆垛机,单一平均作业效率δsin为1.47分钟/盘,即40盘/小时,复合平均作业效率δcom为2.23分钟/2盘,即53盘/小时。根据出入库实际数据可知,堆垛机的单一作业概率sin为11%,复合作业概率com为89%,堆垛机空闲率π为15%。单台堆垛机系统综合出入库作业能力ω定义为:
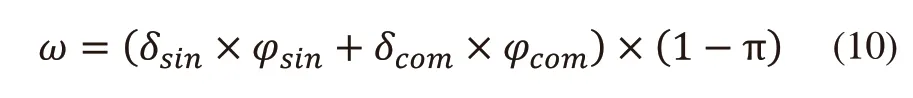
单台堆垛机的入库能力μ2和出库能力μ3分别定义为:
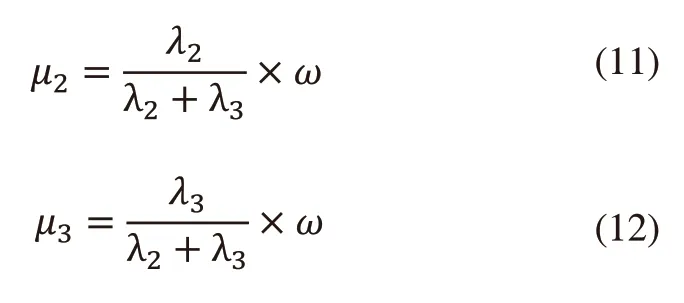
由于入库流量λ2为527托盘/h,出库流量λ3为347托盘/h,所以可以得到:ω=43.8盘/小时,μ2=26.4托盘/h,μ3=17.3托盘/h。由式(1)得系统服务强度ρ2=19.9,ρ3=20.05,故堆垛机的数量应该大于等于21台。
3)拆垛系统
出库系统得出库流量即为拆垛系统的输入流量λ4为347托盘/h,拆垛机器人的拆垛能力μ4为9s处理1件货物,即μ4=66.6托盘/h,所以可得系统的服务强度ρ4为5.21。故拆垛机器人的数量需要大于等于6台。
2.3 各环节排队模型数据分析
如图5所示,根据式(7)和式(9)计算出各环节服务台数量变化时的货物平均等待时间和服务台运行效率。值的注意的是,式(4)平均队长和平均等待时间成正比,系数为λ,曲线趋势完全一致,故不画出。
如图5(a)所示,服务台数量为10台时是曲线的拐点,此时ρs1<1,码垛系统稳定;如图5(b)所示,服务台数量为22台时是曲线的拐点,此时ρs2<1且ρs3<1,入库、出库系统稳定;如图5(c)所示,服务台数量为7台时是曲线的拐点,此时ρs4<1,拆垛系统稳定。
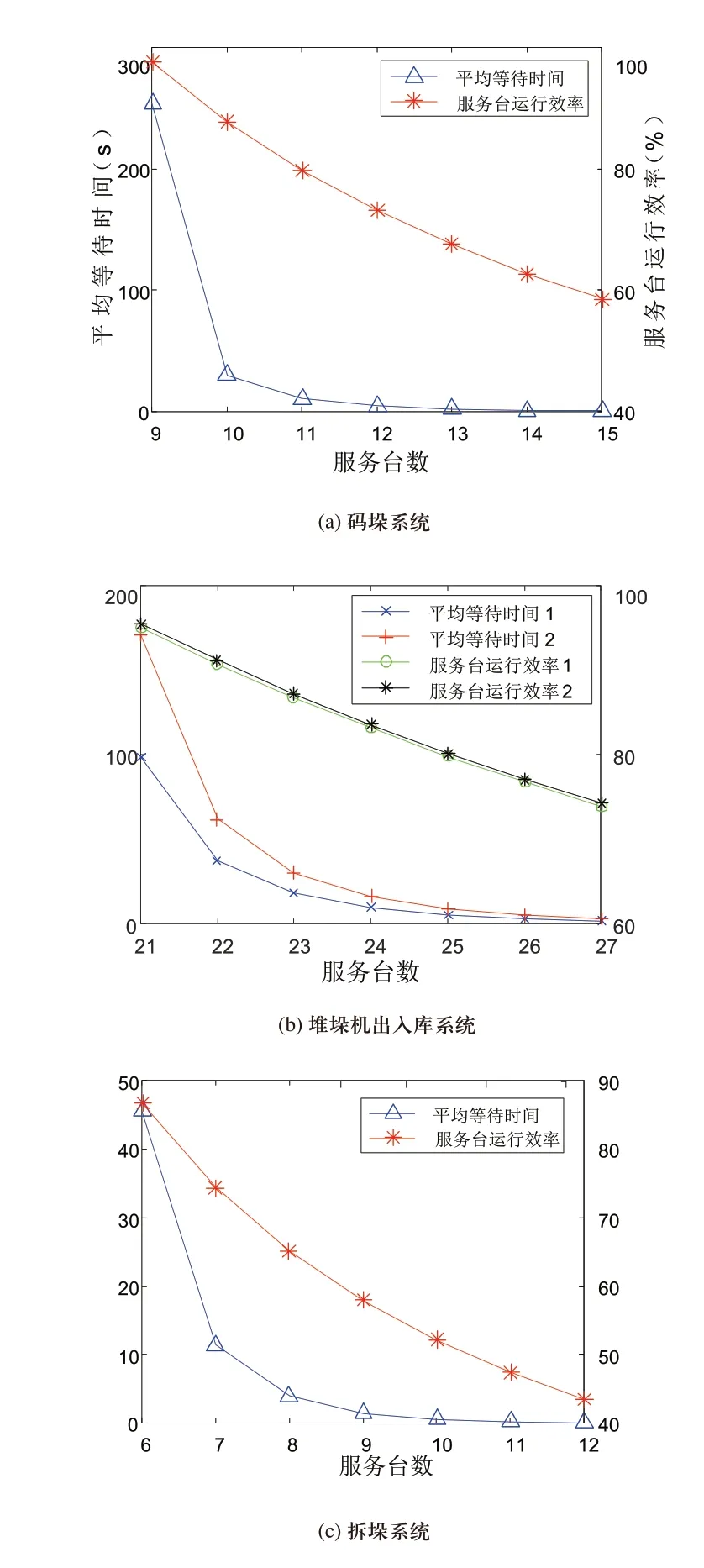
图5 物流仓储系统各环节不同数量服务台曲线图
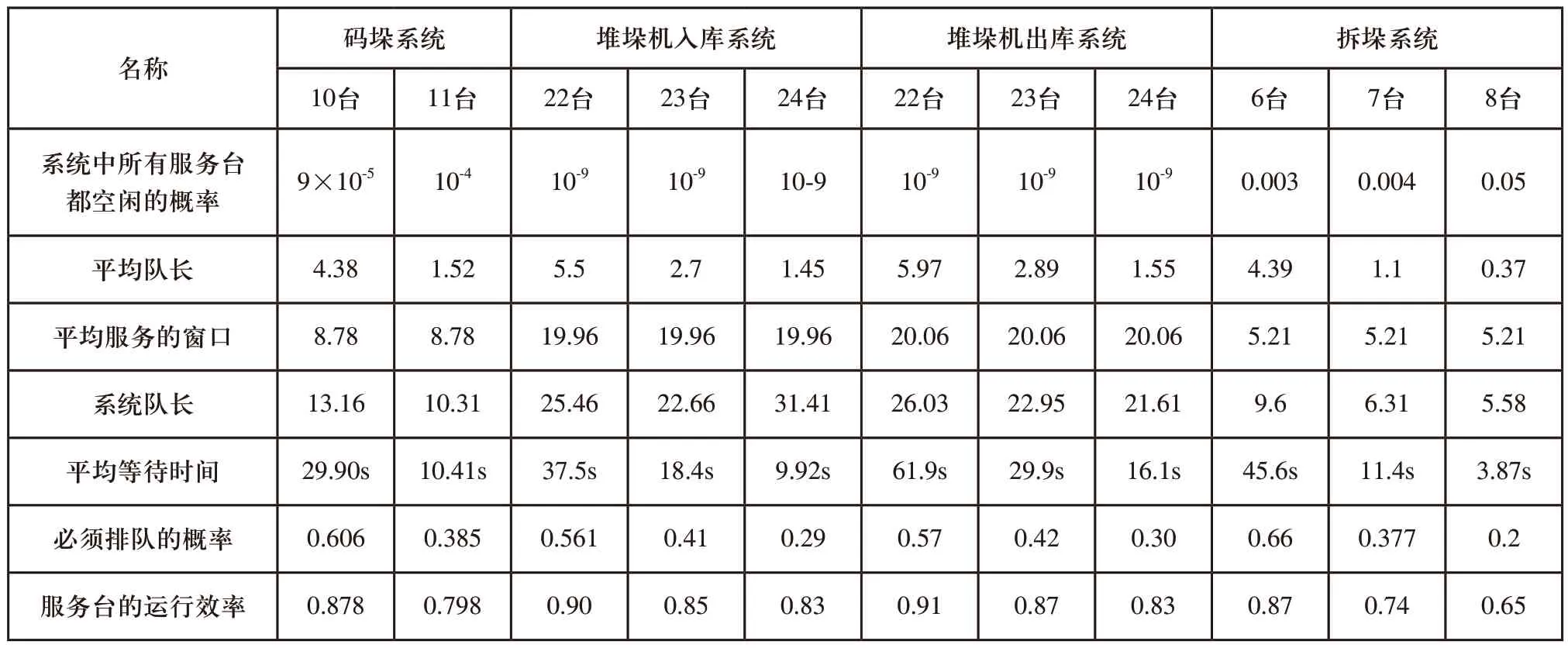
表1 物流仓储系统各环节排队模型参数
各环节服务台数量在拐点附近确定。根据式(1)~式(9)计算出各环节拐点附近部分服务台数量的评价指标数据,如表1所示
1)码垛系统
当码垛机器人数量为10台时,平均队长Lq为4.38个托盘(26.28件货物),货物的平均等待时间Wq为29.9s。对于码垛系统来说,输入端堵塞的是货物,不是托盘,系统拥堵情况有点严重,等待时间过长,会影响效率,所以需要通过增加码垛机器人来优化排队系统,减少排队队长和排队时间。码垛机器人增加至11台时,平均队长Lq为1.52托盘(9.12个货物),货物的平均等待时间Wq为10.41s,与10台相比,明显减少了排队拥堵和等待时间,提升了整体运行效率。
2)入库、出库系统
堆垛机数量为22台时,等待时间过长影响效率。堆垛机增加至23台时,入库、出库等待时间分别减少了50.94%和46.15%。堆垛机增加至24台时,入库、出库等待时间分别减少了73.58%和74.05%。并且综合考虑到堆垛机系统的容错率,堆垛机为24台时,显著地减少了等待时间,优化了出入库系统。
3)拆垛系统
考虑到系统的容错性和冗余量,当拆垛机器人数量为7台或8台时,平均队长和等待时间与6台相比有明显提升,并且7台和8台效果差距不大。因此A厂可结合投入预算,自行选择7台或8台拆垛机器人。
3 仿真分析
3.1 仿真建立
建立物流仓储系统动态模型,设仿真时间为t,在t时间内,顾客到达总量为m。顾客的到达过程服从泊松分布,第n个顾客的到达时间间隔为an。服务台的服务时间服从负指数分布,服务台为第n个顾客服务的服务时间为sn。第n个顾客到达系统的时间间隔为An,系统为第n个顾客开始服务的时间为Bn,第n个顾客离开系统的时间为Cn。有公式:
第n个顾客的到达时刻An为:
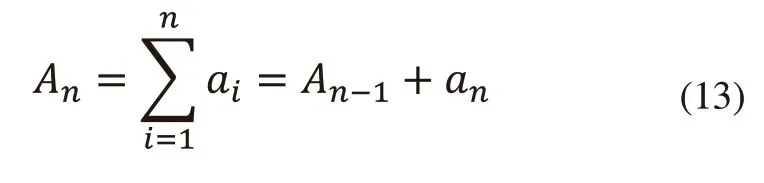
系统为第n个顾客开始服务的时间Bn为:

系统中所有顾客的平均等待时间Wq为:
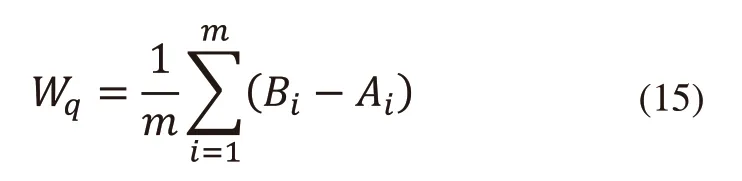
3.2 仿真数据
采用3.1节中建立的仿真模型对码垛系统进行仿真,仿真结果如图8、图9所示。当码垛机器人数量设置为11台,货物数量为200件时,得到平均等待时间为10.05s,平均队长为1.47件。例如,第101件货物的到达时间为585.8s,服务时间为14.6s,等待时间为10.6s,当前排队数量为8件,离开时间为611.1s。
10台和11台码垛机器人进行15次仿真实验,货物数量为5000件的数据如表2所示。
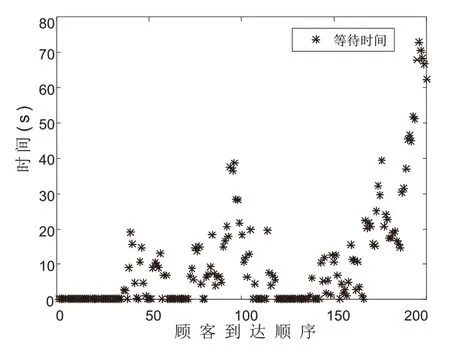
图8 11台码垛机器人等待时间仿真图
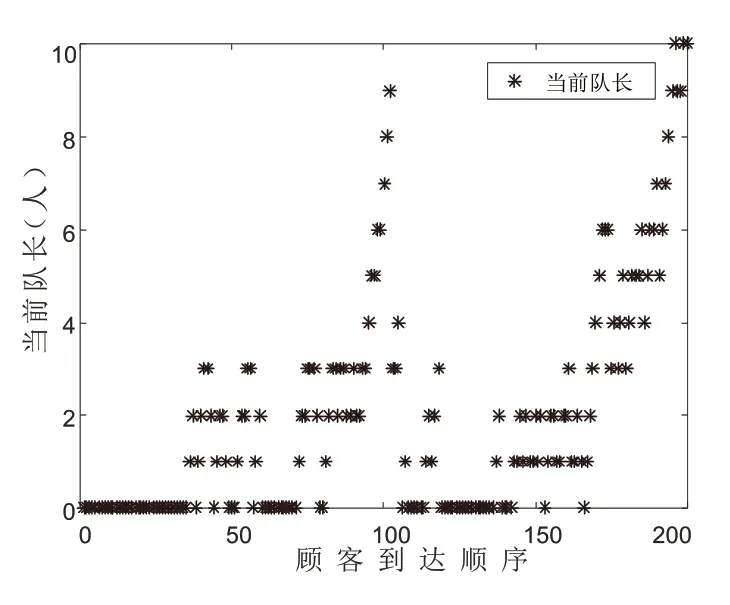
图9 11台码垛机器人队长仿真图
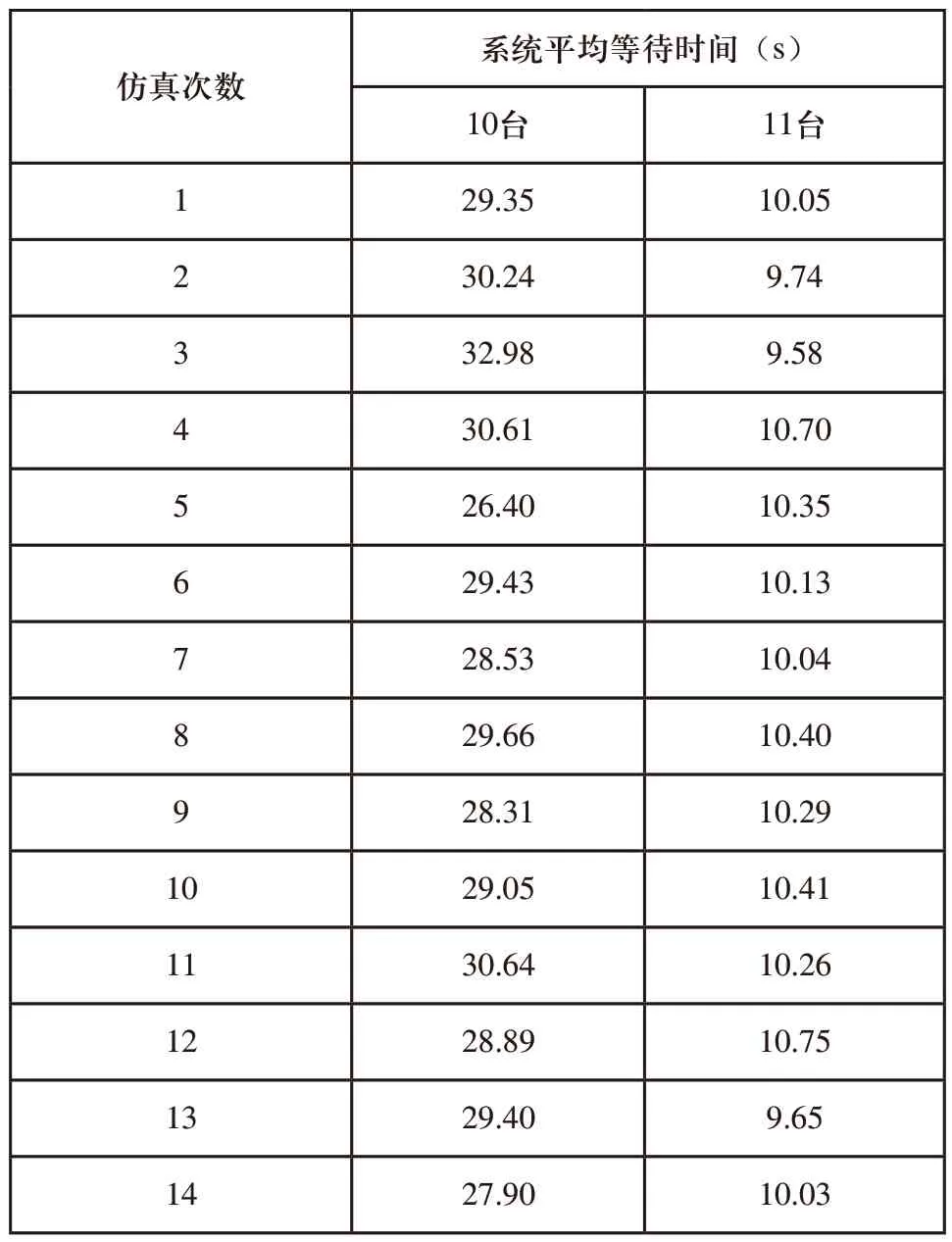
表2 码垛系统仿真数据
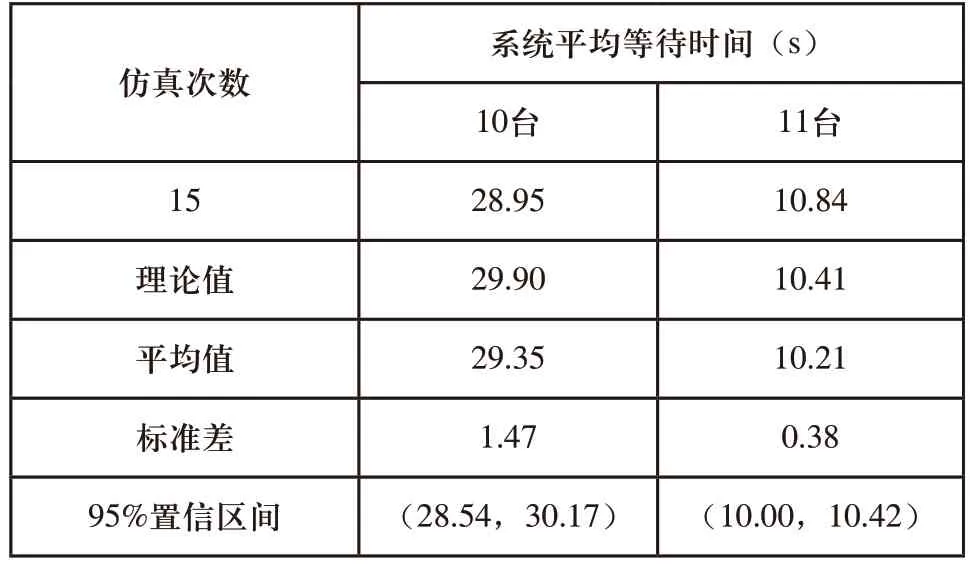
表2(续)
样本数据服从正态分布,运用数理统计计算出样本的平均值、标准差和95%置信区间。10台码垛机器人时,平均排队时间的理论值为29.9s,样本得出的95%置信区间范围为(28.54,30.17),理论值在置信区间内,说明排队理论运用在码垛系统中合理。11台码垛机器人同理。
出入库系统和拆垛系统仿真结果如表3所示。各系统的理论值均在95%置信区间内,说明排队理论运用在各系统合理。
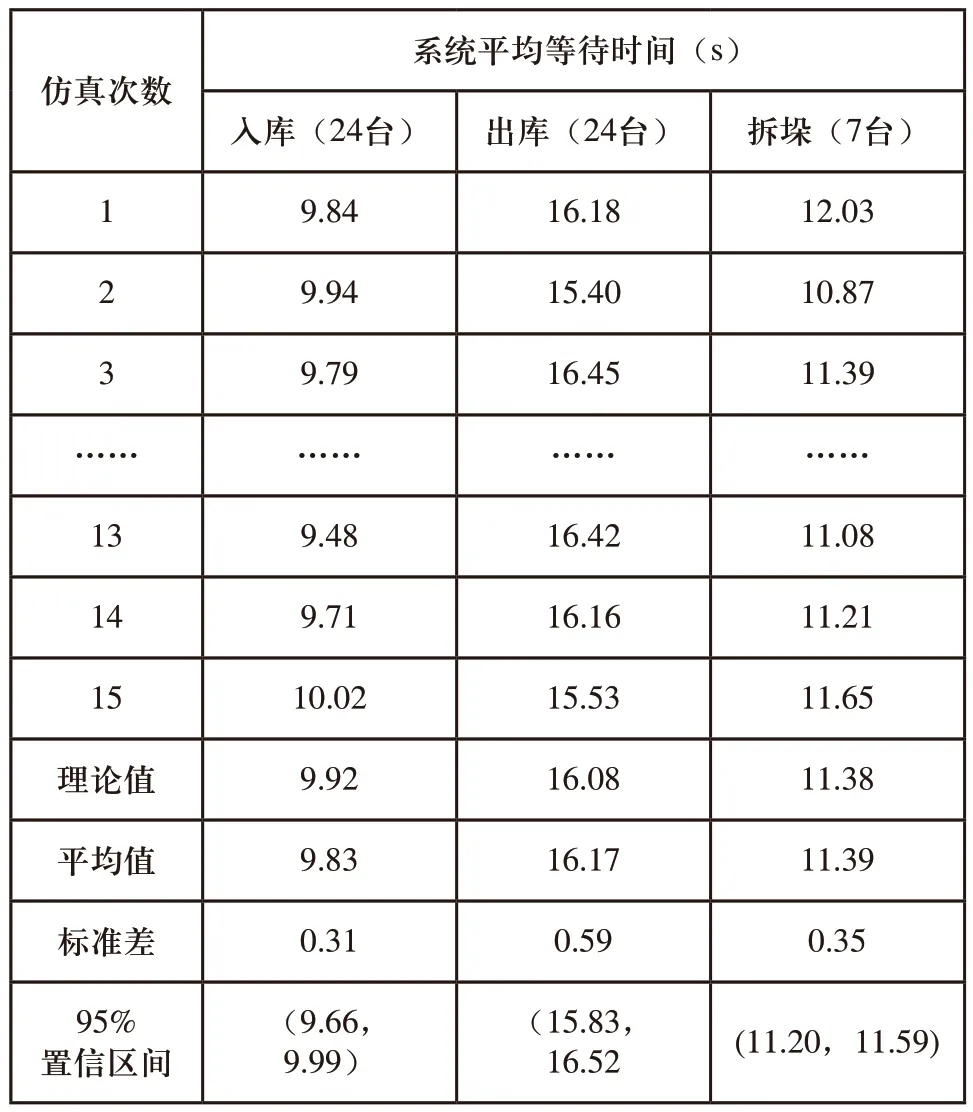
表3 出入库和拆垛系统仿真数据
4 结语
本文提出了一种基于排队理论规划自动化物流仓储系统的方法,并针对系统各环节进行分析。通过数学建模得出指标参数,求出最优方案。通过仿真验证排队理论运用在该系统的合理性。同时为A厂节约了成本投入,提高了物流效率。
自动化物流仓储系统还有许多其他的环节,例如环穿车系统、AGV系统等。鉴于篇幅有限,其他环节也可用类似的方法进行研究,因此本文不再赘述。
