往复式自动化压缩机管道结构减振方法研究
2020-08-13余思颖吴晓南苟珈源
余思颖,吴晓南,苟珈源
(西南石油大学 土木工程与测绘学院,成都 610500)
0 引言
管道系统是流体输送设备,在化学化工、石油化学等领域中均有广泛应用,但是目前还没有提出与管道设计相关的振动校核方法,导致管道的振动问题[1],从而在生产过程中带来一些危害,例如管道系统的结构和管路的附件发生疲劳损坏、管道保温材料破损、控制系统产生误动作、测量仪器仪表失真以及导管破坏、阀片磨损至损坏等,在这些危害中对压缩机的工况影响是最为严重的,也是生产过程的关键。往复式压缩机管道系统的振动会导致管路附件发生破裂会松动,造成管道泄漏,甚至会引起管道爆炸[2,3]。因此对往复式压缩机管道结构减震方法进行研究具有重要的现实意义和理论意义[4]。
丁继超[5]等人提出基于ANSYS模拟分析的管道结构减震方法,该方法根据现场管道振动情况通过ANSYS模态分析获得压缩机管道振动的原因,在阻尼减震原理的基础上对阻尼减震的可实时性进行分析,并通过SAP2000阻尼进行减震仿真,根据仿真结果获得管道结构减震的最佳方案,但是该方法不能准确的对管道振动原因进行分析,导致精准度低问题。涂瀚[6]等人提出基于Fluent软件的管道结构减震方法,该方法通过Fluent软件对侧压管内压力分布和管道压力反馈时空压机主管道的压力分布进行数值计算,根据数值计算结果,设计管道结构减震方法,该方法减振后的管道振动速度峰值较高,存在减振效果差的问题。
为解决上述方法中存在的问题,提出往复式压缩机管道结构减震方法,在气流脉动分析理论的基础上结合管道模态特性分析结果,实现往复式压缩机管道结构的减振。
1 管道模态特性
管道结构系统在往复式压缩机内的振动微分方程为:
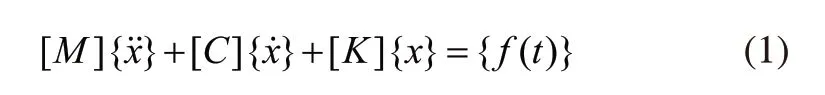
对于往复式压缩机管道结构的自由振动,即无激励力、无阻尼的振动[7],管道结构对应的振动微分方程如下:
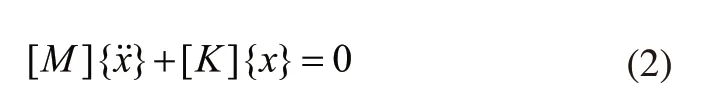
下式为线性系统方程对应的通解形式:
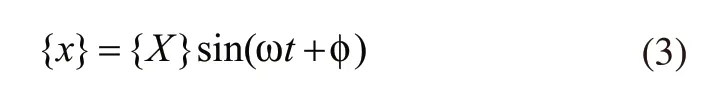
结合式(2)和式(3)获得下式:
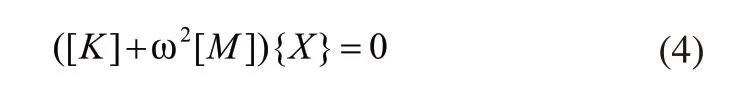
管道结构的节点在自由振动时的位移不能全是零,因此式(7)需要存在非零解,即:
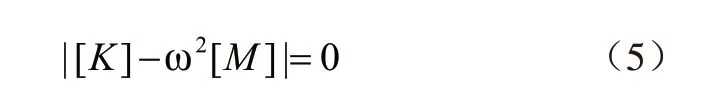
上式方程为频率方程,存在n个自由度的往复式压缩机管道结构系统中具有n个根ω1,ω2,…ωn,ωn表示往复式压缩机管道系统对应的第n阶固有阶段,将其代入式(6)中,获得下式:
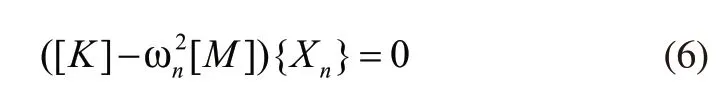
式中,{Xn}代表的是振型向量,表示往复式压缩机管道结构的固有振型。
1.1 管道的轴向振动
设l代表的是往复式压缩机管道长度;A(x)代表的是压缩机管道的截面积;P表示往复式压缩机管道轴向截面微元中存在的力。
当单位长度的压缩机管道中的作用力为f(x,t)时,力平衡方程如下:
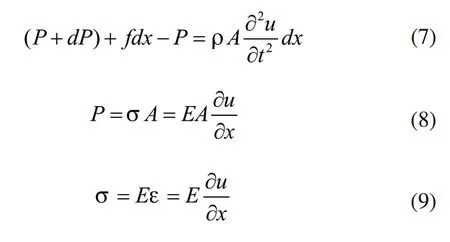
式中,P表示轴向力;ρ代表的是管道结构的密度;E表示杨氏模量;u表示轴向位移;σ 表示轴向应力;ε表示轴向应变。
在几何关系的基础上,获得下式:

对往复式压缩机管道的振动方程进行简化,获得下式:
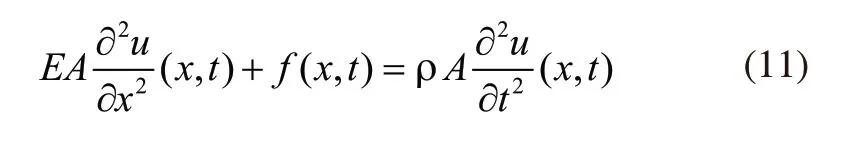
对于往复式压缩机管道的自由振动,f(x,t)的值为零,存在下式:
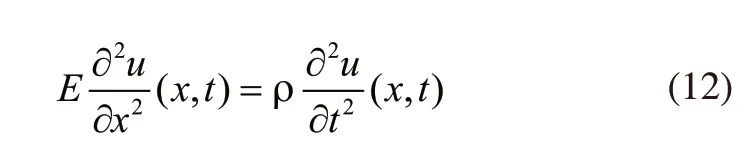
可以通过分离变量法对管道的轴向振动方程进行求解[8],假设U(x)、T(t)分别独立于x、t,获得u(x,t)的通解:
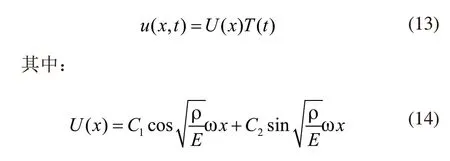
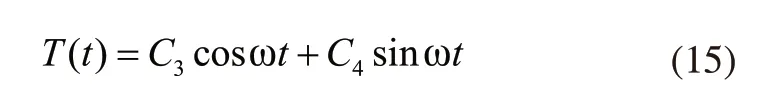
式中,ω代表的是往复式压缩机管道对应的轴向振动角频率;C1、C2、C3、C4均为常系数,通常由边界条件和初始条件确定。
以长度为l的往复式压缩机管道为例,自由端的应变为零,固定端的位移为零,对应的边界条件如下:
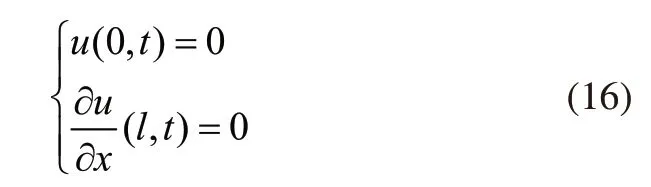
在式(16)的基础上获得下述公式:
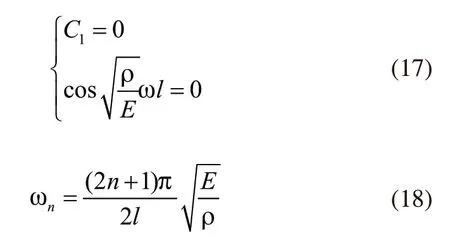
通过上述分析,获得固有频率f的计算公式:
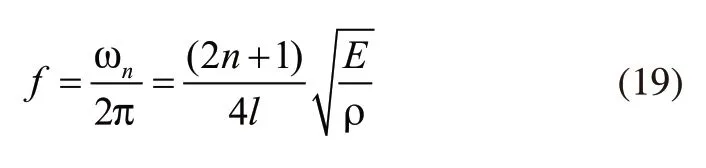
因此振型函数Un(x)的表达式如下:
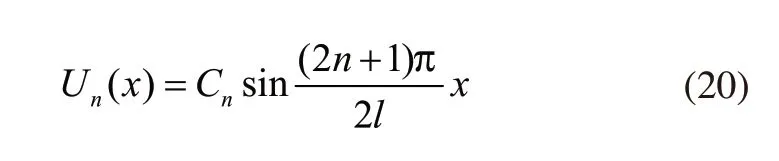
1.2 管道的横向振动
在管道力矩平衡方程和力平衡方程的基础上获得下式:
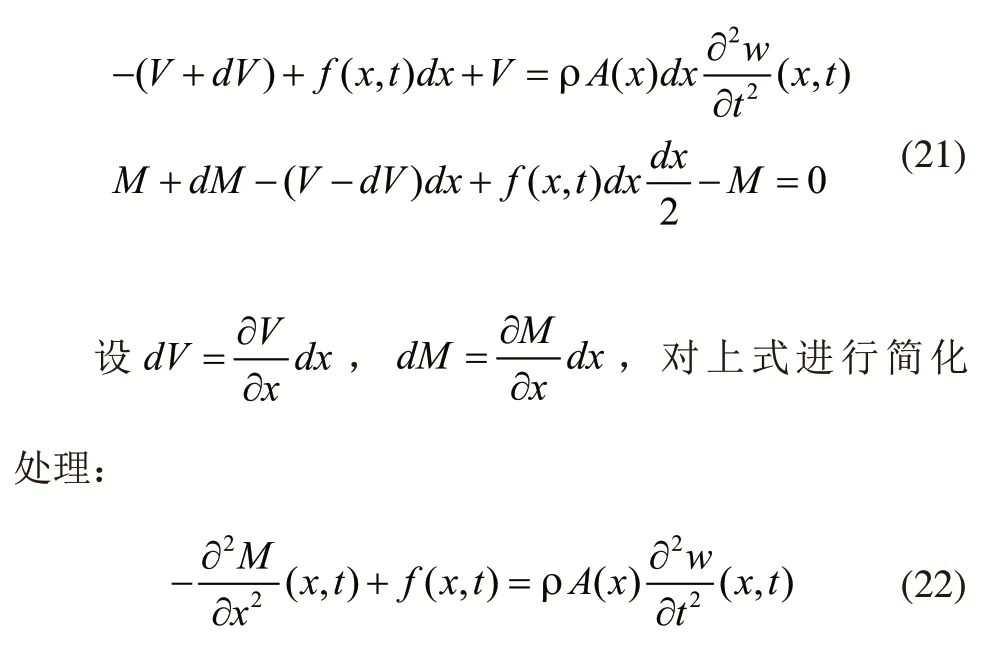
变形和弯曲力矩之间存在的关系可以在欧拉-伯努利梁理论的基础上获得[9]:
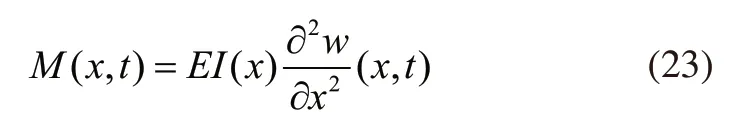
式中,I(x)表示y轴中存在的惯性矩。
通过上述分析获得往复式压缩机管道的受迫振动方程:
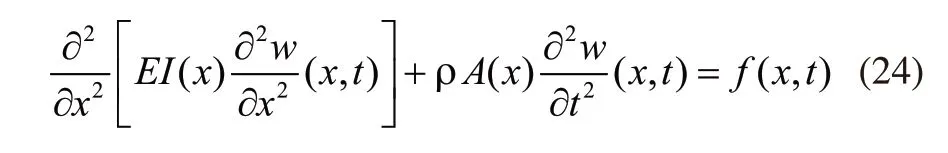
对于均匀截面的往复式压缩机管道,对上式进行简化:
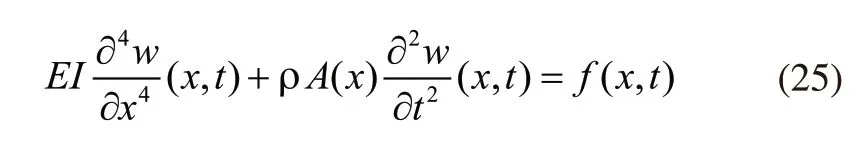
f(x,t)的值在自由振动时为零,此时自由振动方程的表达式如下:
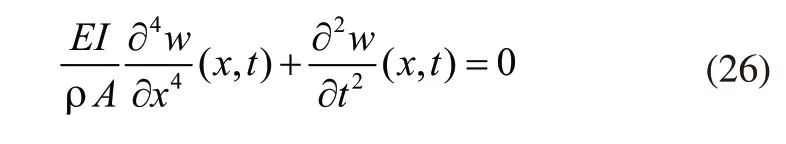
通过分离变量法对振动方程进行求解:
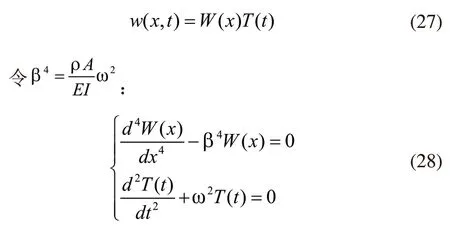
通过上述公式,获得方程的通解:
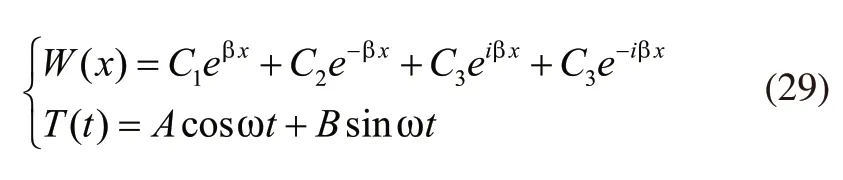
在双曲余弦、双曲正弦和欧拉公式的基础上获得振型函数W(x)的表达式:
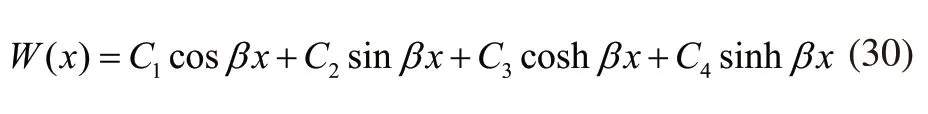
2 管道结构减震方法
可以通过消减气流脉动降低管道振动,实现往复式压缩机管道结构减震。
2.1 气流脉动分析理论
平面波动理论是气流脉动分析的基础,管道内存在的气流,由于压缩机的周期运动,形成了介质稀疏与稠密相间隔的压力脉动气流,波的传播方式与上述传播方式相似,因此可以参考波的传播现象对压缩气流在压缩机管道内的传播现象进行描述[10]。在波动方程的基础上对气流脉动在往复式压缩机管道内的平面波动进行计算。下式为平面波动方程:

式中,p表示管道I处流体在某时刻的压力。
通过传递矩阵法对气柱固有频率进行计算:
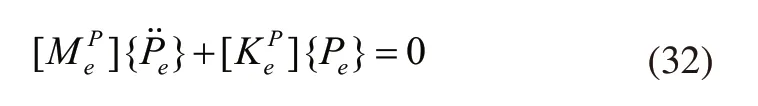
设气体在往复式压缩机管道内做简谐振动,此时存在下式:

式中,ω表示振动角;A表示振动向量。结合式(32)和式(33)获得下式:
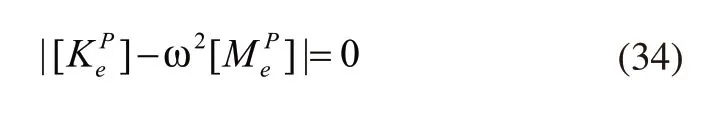
当气柱固有频率和管道结构固有频率在压缩机激振频率的共振区内时,往复式压缩机管道结构此时会发生共振[11],设fex代表的是压缩机激振频率,可通过下式计算得到:

式中,n表示压缩机转速;m表示压缩机气缸作用方式。
2.2 减震方法
2.2.1 设置缓冲罐
在往复式压缩机气缸的排气口或进气口周围安装缓冲罐,隔离往复式压缩机管道与气缸。缓冲罐的主要作用是消减脉动的气流,使脉动在往复式压缩机管道内变得轻微。管道系统内的固有频率可以通过缓冲罐得以改变,提高缓冲罐与气缸之间的气柱固有频率值,避免往复式压缩机管道的低阶气柱共振;足够大的缓冲罐在往复式压缩机管道内起到稳压作用;缓冲罐对高频波具有明显的衰弱作用,是一种低通滤波器[12]。
1)缓冲罐容积
通过下述公式对脉动抑制装置的最小初始容积进行计算:
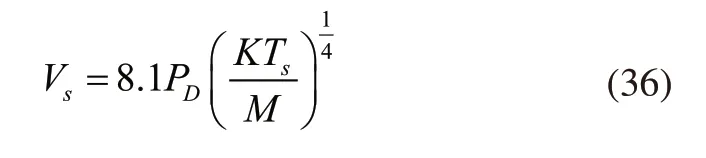
式中,Vs表示需要的最小吸入缓冲容积;PD表示净容积;K表示气体的等熵压缩指数;M表示气体分子量;Ts表示入口绝对温度。
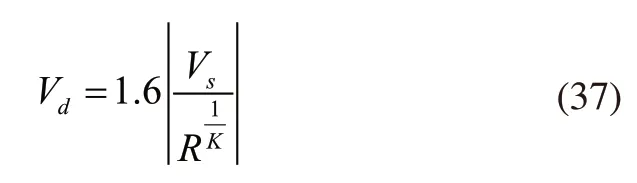
式中,Vd表示需要的最小排出缓冲容积;R表示气缸处的压力比。
2)缓冲罐的配置方式
越靠近气缸,缓冲罐的缓冲效果越好,缓冲容积距离气缸较远时越大,缓冲效果较好。安装缓冲罐时,在空间允许的情况下尽量直接与气缸排气口、进气口相连。
3)缓冲罐的形状
缓冲罐存在两种形式,分别是球形和圆筒形,两种形式具有相同的容积,无论从消减气流脉动的角度,还是从容器受力的角度进行考虑,球形缓冲罐更优越[13]。
2.2.2 设置集管气
多台往复式压缩机并联运行过程中,为了控制脉动气流的压力不均度在规定范围内,需要使用集管气。为了提高脉冲效果,集管气的流通面积要大,同时要考虑集管气分支管的长度。
2.2.3 调整气柱固有频率
在设计配管过程中,需要对往复式压缩机管道的气柱固有频率进行计算,通过调整气柱固有频率避免产生1~3阶的气柱共振。可以通过改变盲管的配置、管道长度、分支管的增减、管径、容器位置和容器大小对气柱固有频率进行调整。
3 实验结果与分析
为了验证往复式压缩机管道结构减震方法的整体有效性,需要对往复式压缩机管道结构减震方法进行测试,本次测试采用的操作系统为Windows 64位。
对往复式压缩机管道结构进行减震时,需要对往复式压缩机管道的振动特性进行分析,分别采用往复式压缩机管道结构减震方法、文献[5]提出的基于ANSYS模拟分析的管道结构减震方法、文献[6]提出的基于Fluent软件的管道结构减震方法进行测试,对比不同方法的分析精准度,测试结果如下:
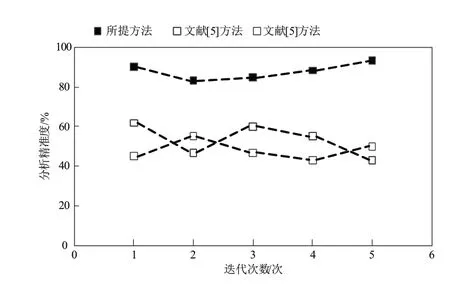
图1 不同方法的分析精准度
分析图1可知,在多次迭代中所提方法的分析精准度均高于文献[5]方法和文献[6]方法的分析精准度,因为所提方法通过管道的轴向振动和管道的横向振动对管道的振动特性进行分析,提高了方法的分析精准度。
在管道结构中设置5个测试点,对比所提方法、文献[5]方法、文献[6]方法减震前后的振动速度峰值,测试结果如下:
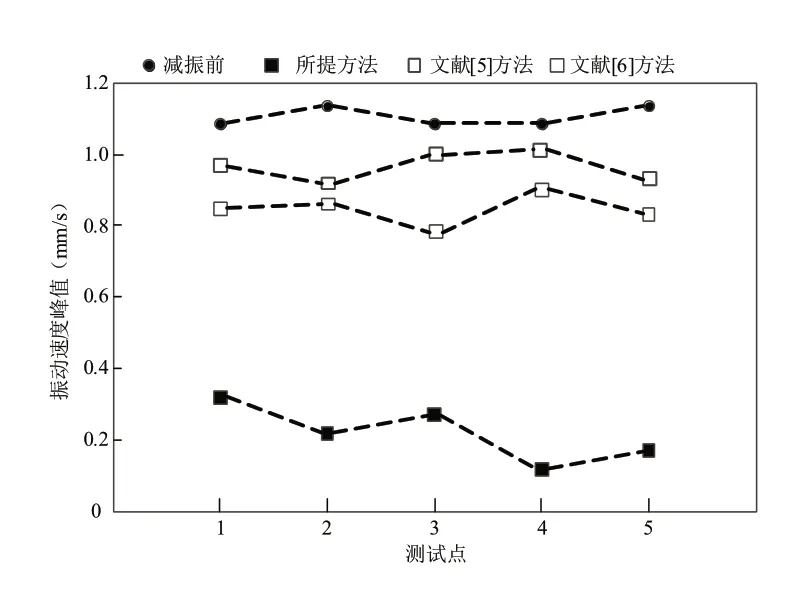
图2 不同方法的振动速度峰值
将所提方法、文献[5]方法、文献[6]方法减振后测点的振动速度峰值与减振前测点的振动速度峰值对比可知,采用所提方法对往复式压缩机管道结构进行减振后,各个测点的振动速度峰值明显下降,文献[5]方法、文献[6]方法对往复式压缩机管道结构进行减振后,各个测点的振动速度峰值下降的不明显。对比所提方法、文献[5]方法、文献[6]方法的测试结果可知,所提方法的减振效果较好。
4 结语
往复式压缩机在天然气加工、集输、开采等领域中得到了广泛的应用,但往复式压缩机间歇性的工作方式,在不同程度上容易导致管道发生振动,往复式压缩机管道结构发生振动时会导致仪器仪表失真、管道结构疲劳损坏等问题,甚至会引起爆炸、气体泄漏和管道断裂等事故,因此需要对往复式压缩机管道结构进行减振处理。当前管道结构减振方法存在分析精准度低和减振效果差的问题,提出往复式压缩机管道结构减振方法,对管道结构的振动特性进行分析,根据分析结果对管道结构进行减振处理,为往复式压缩机的安全工作提供了保障。
