多级圆柱直齿轮轮系传动比优化设计研究

王宝超，张培培，孙浩沩，尚鹏飞

（1.中机生产力促进中心，北京 100044；2.电子科技大学，成都 611731）

0 引言

轮系传动比分配方法一般是设计者根据已知的各种装置工况，在机械设计手册所推荐的范围内选择一组合适的传动比，这样往往主观性太强，使得设计随意性和误差较大。设计者所选择的传动比是否为最优，并没有严格的数学验证和实际的工程验证。与传统的盲目选择传动比相比，已有很多关于传动比和传动级数选择优化的研究工作。比较早的研究是余茂芃[1]和齐人光[2]，他们进行了详细的模型推导。罗登峰[3]和范舟[4]在轮系设计方法提出了优化思想。廖仁文等[5]和朱文峰[6]在轮系传动比分配中提出了多目标优化的方法。李阿楠[7]和关维娟[8]等将轮系优化设计在MATLAB中实现，实现了模型和优化算法结合。

另外Thompson等人[9]是以变速器体积最小为优化目标，以满足表面接触强度的基本要求出发建立数学模型，通过模型求得最优的传动级数和各级传动比。Chong等[10]从轮系的传动误差的最大值出发建立数学模型，在分析齿轮固有误差，安装误差以及回转误差对运动精度的影响下，以轮系在啮合传动过程中产生的转角误差与传动比的关系来求得最优的传动比分配方案。

这些文献很多都是运用轮系的总体积，总转动惯量，总转动误差进行优化。但是在关于轮系传动比分配方案，一般遵循的原则是，使得轮系外轮廓尺寸较小，结构较紧凑，重量轻，有足够的承载能力且转动惯量较小，传动误差小，传动精度高，传动平稳等。

因此文本未直接运用轮系的总体积，总转动惯量，总转动误差，而是从设计原则出发，设置了三个无因次变量，即体积比V，转动惯量比J，以及转角误差比β，建立其传动级数和传动比之间的数学模型，并进行优化，从而得到设计轮系需要最优级数和传动比。

论文安排如下：第1部分为轮系传动比分配数学模型的构建；第2部分为传动比分配的优化和结果分析；第3部分为总结。

1 轮系传动比分配数学模型的构建

1.1 多级圆柱直齿轮轮系分析

多级圆柱直齿轮轮系传动装置（如图1所示），总传动比为I，传动的总级数为N，且任意一级的小齿轮齿数相差不大。要求设计出一个转动惯量J较小，结构较紧凑，且传动误差较小，传动精度高的多级圆柱直齿轮轮系。

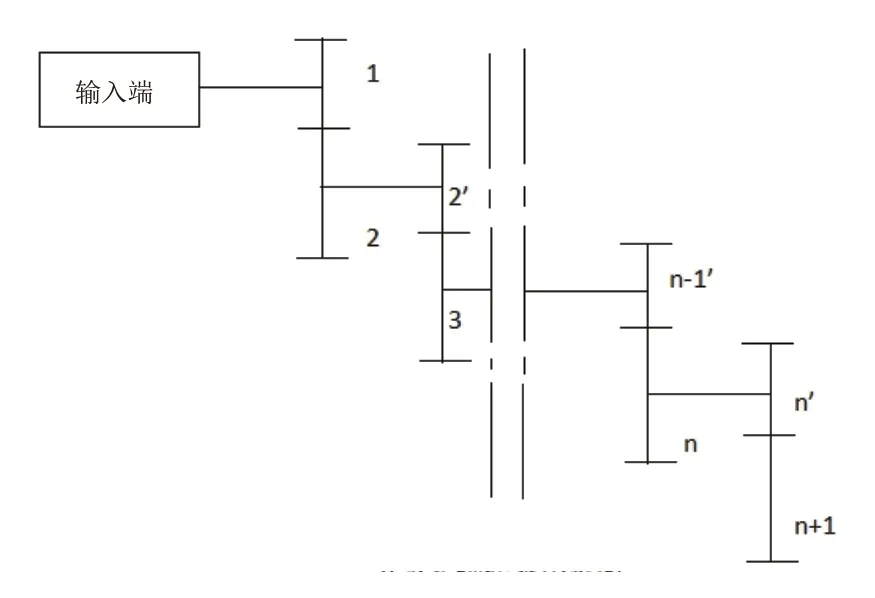
图1 n级定轴轮系示意图

首先设立数学模型中的变量：已知该多级圆柱直齿轮轮系的传动总级数为N，所以自变量为每一级的传动比，将每一级的传动比假设为：Xj（j=1，2，3，…，n），其为第j级的传动比。

根据多级圆柱直齿轮定轴轮系的传动特点得到如下约束：

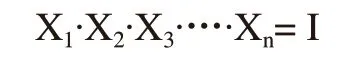
其中，1-Xj·＜ 0，j=1，2，…，n。

从模型构建的出发点来看，为了实现多级轮系的转动惯量比J小，结构紧凑也就意味着体积比V最小，还有就是传动误差比β小即传动的精度高。

为了统一目标，运用线性加权将三者合起来，即：转动惯量比J，体积比V，传动误差比β，得到多级圆柱直齿轮轮系最优的传动级数以及最优的各级的传动比。

1.2 传动级数和各级传动比与转动惯量比的单一模型

前提假设为：各小齿轮转动惯量相同；轴和轴承的转动惯量忽略；各个齿轮均是实心圆柱体便于计算而且齿宽和材料相同。

设：Je为等效到输入轴上的转动惯量；J1为主动齿轮相对于自身的转轴转动的转动惯量；J2为从动齿轮相对于自身的转轴转动的转动惯量。

对于n级圆柱齿轮传动，第k级的传动比为：

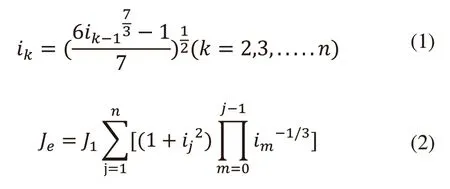
式中用xk表示传动比ik，所以轮系的转动惯量比与轮系的传动比建立的目标函数为：

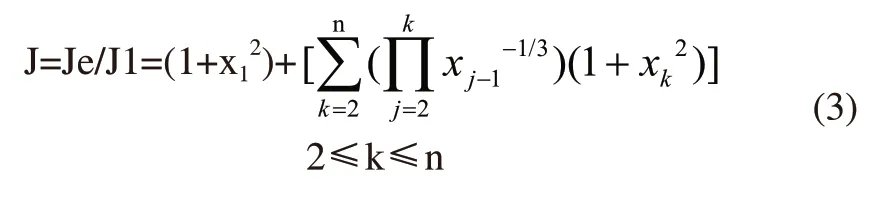
1.3 传动级数和各级传动比与体积比的单一模型

前提假设为：每一级小齿轮体积相差不大，也就是说质量相近。每一个齿轮为实心圆柱体便于计算而且齿宽和材料都相同。由于第一个和第二个齿轮体积为v1和v2（式(1)和式(2)），根据其传动比，换算得到第二个和第三个齿轮的体积（式(6)和式(7)）。

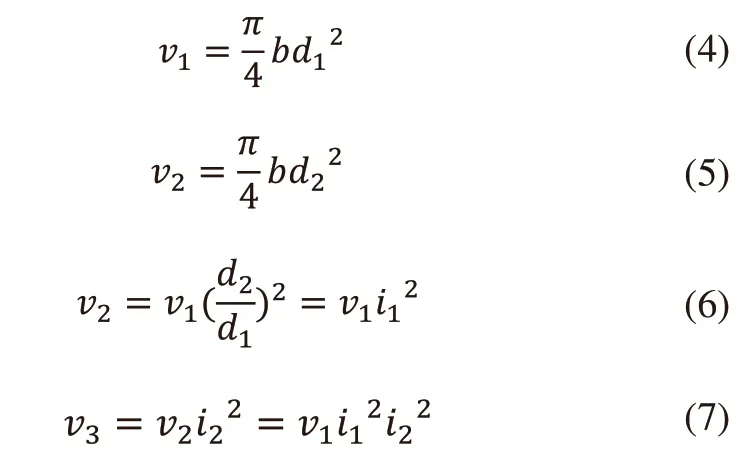
所以轮系的总体积为：

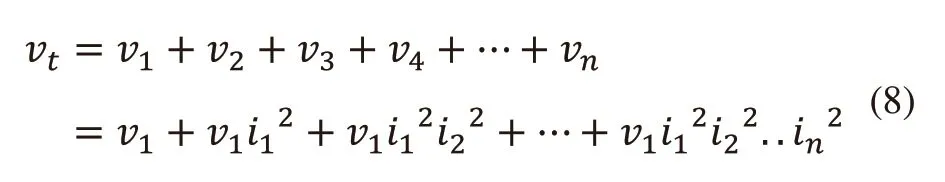
体积比即体积的无因次系数：

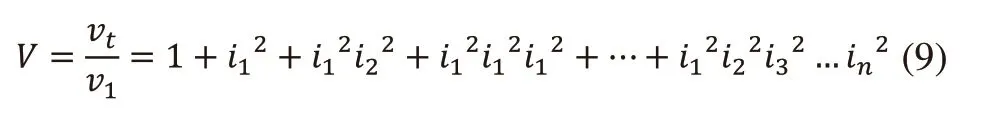
V为总体积与第一个齿轮体积的比值，为体积的无因次系数。所以轮系的体积比与轮系各级的传动比建立的目标函数为：

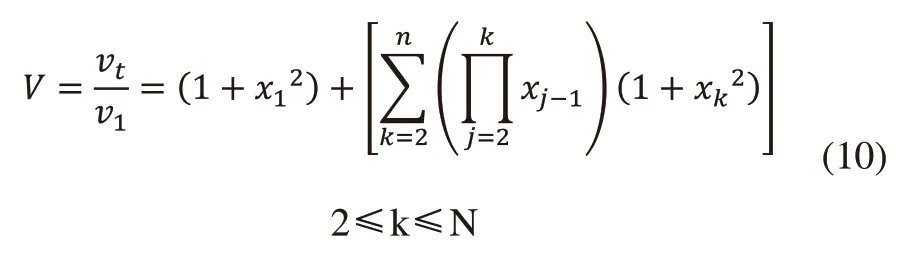
1.4 传动级数和各级传动比与传动误差比的单一模型

对于表示圆柱直齿轮轮系的传动精度，因为每一级都会存在转角误差，而总系统的误差是由于各级轮系从动轮的转角误差叠加造成的，如果假设圆柱直齿轮传动轮系中各级从动轮的转角误差均相等的话，可以根据之前的假设推出：

一级齿轮传动的转角误差β1：

二级齿轮传动的转角误差：β1+β1i1；

三级齿轮传动的转角误差：β1+β1i1+β1i1i2；

n级齿轮传动的转角误差：

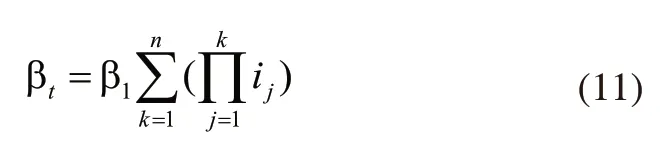
式中的β为类似于之前提到的转动惯量比J以及体积比V的转角的无因次系数；βt为圆柱齿轮轮系的总的转角误差；β1为第一级传动的转角误差。所以圆柱直齿轮轮系传动比与轮系的转动误差比，转动精度建立的目标函数为：

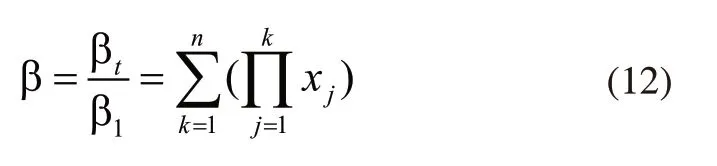
1.5 传动级数和各级传动比与三个无因次变量的耦合模型

基于所建立的三个目标函数，可以分别讨论圆柱直齿轮轮系中转动惯量比J与各级传动比，体积比V与各级传动比，以及传动误差比β与各级传动比的关系，但为了使研究优化的结果更为精确更符合实际情况且达到最优的效果，本文采取综合考虑转动惯量比J，体积比V还有转动误差比β三者与轮系的传动级数n各级的传动比ik的关系。

设总的目标函数为F为F（x1，x2，…，xn）即变量为总级数n以及每一级的传动比ik。

设a1为转动惯量比的线性加权系数，a2为体积比的线性加权系数，a3为传动误差比的线性加权系数，其总和为1（a1+a2+a3=1），于是总的目标函数（要求最小）可以表示为：

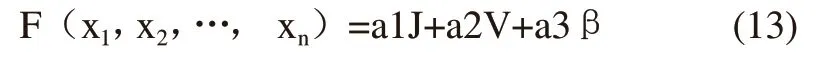
2 优化结果和分析

2.1 优化过程说明

若多级轮系的总的传动比为I，传动级数N，假设每一级的小齿轮的齿数z相同，求解并且设计的多级传动装置的转动惯量比J最小、结构最紧凑而且传动精度最高传动误差最小的多级定轴圆柱齿轮传动的轮系。为了研究各个目标与级数n还有每一级传动比ik的大小是否有关系，研究过程分为：单独研究转动惯量比即转动惯量的无因次系数与传动比的关系；单独研究多级轮系的结构是否紧凑与传动比的关系，用体积比V来表示，这里的体积比为多级圆柱直齿轮轮系的总体积与第一级中的小齿轮的体积的比值，为一个无因次无单位的系数；单独研究多级轮系的传动误差即传动精度与传动比的关系，转动误差可以用传动的转角误差β来表示；得到每一个分目标函数与传动级数n以及各级传动比ik的关系之后将三个分目标函数结合成一个总的目标函数，即每一个分目标函数前面乘上相关的系数，之后求和从而得到总的目标函数，然后再分析优化总目标函数与传动级数n和各级传动比ik的关系，最终得出最优的结果，即在多级圆柱直齿轮轮系总传动比为一个定值时，得出最优的传动级数n，并且求得每一级的传动比ik，最优的级数以及每一级的传动比确定后，应用于到实际的多级圆柱直齿轮轮系的设计中去，从而为实际生产实践提供最优的参考。

2.2 传动级数和各级传动比与转动惯量比的单目标优化

对于转动惯量比J与传动级数n以及各级传动比ik，为了使多级圆柱直齿轮轮系的转动惯量比J最小，可求解得除最优的级数n和各级传动比ik的大小。

假设多级圆柱直齿齿轮轮系总传动比为I=100，运用序列规划方法（SQP）求解目标函数（如式(3)所示），最后结果得出最优级数为8级，每一级的传动比如表1所示。

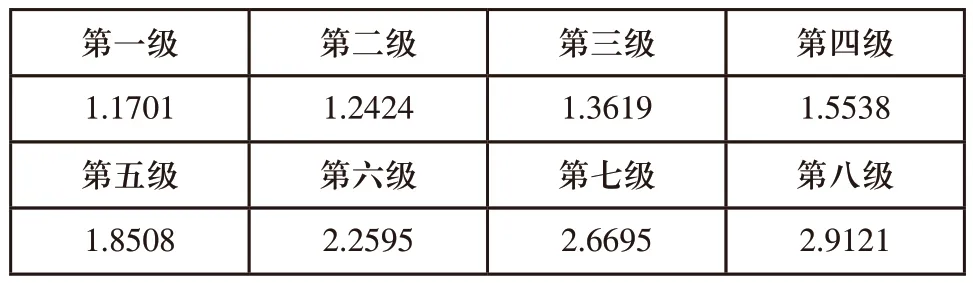
表1 基于转动惯量比各级传动比

传动级数是影响转动惯量的一个因素，图2给出了多级圆柱直齿轮轮系传动级数n与转动惯量比J的关系。

图2 传动级数n与转动惯量比J的关系

从图2可以看出，目标函数多级圆柱直齿轮轮系的转动惯量比J与传动的级数n的关系，可以用一个类似于开口向上的的抛物线来表示，在多级轮系的传动级数小于8级时，随着传动级数的增加，该多级圆柱直齿轮轮系的转动惯量比是逐渐减小的，而且下降趋势是十分明显的，而当多级轮系的传动比大于8级的时候，随着轮系的传动级数的增加，该多级圆柱直齿轮轮系的转动惯量比又是逐渐增加的，而且增加的十分缓慢，并且最终由变为一条定转动惯量比的直线的趋势。而在轮系的传动级数为8的时候，轮系的转动惯量比J处在图中的极小值点，即为最小，再观察这8级每一级的传动比，每一级相比于前一级的传动比略有增大，而通过计算出来的结果可以得知，传动级数为8级时，此时系统的转动惯量无因次系数J的值确实为最小，则此时轮系总传动比为100时，单看转动惯量可以得到最优的级数为8级，因此便于设计者的实际规划级数n。

2.3 传动级数和各级传动比与体积比的单目标优化

对于分析多级圆柱直齿轮轮系的体积比V与传动级数n以及各级传动比ik的关系，目的就是通过构建的数学模型求得最优的级数和各级传动比的大小，从而使的多级轮系的结构最为紧凑。假设所设置的多级圆柱直齿轮轮系总传动比为100，运用序列规划方法（SQP）求解目标函数（如式(10)所示）。最后结果得出最优级数为5级，每一级的传动比如表2所示。

表2 基于体积比各级传动比

传动级数是影响体积比的一个因素，图3给出了多级圆柱直齿轮轮系传动级数n与体积比V的关系。

图3 传动级数n与体积比V的关系

由图3可以看出，目标函数多级圆柱直齿轮轮系的体积比V与传动的级数n的关系，可以用一个类似开口向上的抛物线来表示，类似于转动惯量比J与传动级数的趋势，由图可看出，当传动级数n为5时，体积比V的值为最小，而在传动级数小于5的情况下，多级轮系的体积比下降的十分明显，而当传动级数大于5时，由图可看出，该多级圆柱直齿轮轮系的体积比近似为一条直线，即体积比近似于一个定值，由所绘制的求每一级的传动比的公式，得到的每一级的传动比，可以看出每一级相比于前一级的传动比略有增大，每一级相比于前一级传动比增大差不多0.2左右。当所设置的多级圆柱齿轮轮系总传动比为100时，单看体积比V可以得到最优的级数为5级，因此便于设计者的实际规划级数。

2.4 传动级数和各级传动比与传动误差比的单目标优化

对于传动误差，用传动误差β来表示，研究其与传动级数以及各级传动比关系，是为了求得多级轮系的最优的传动级数n和每一级的传动比ik的大小使的多级圆柱直齿齿轮轮系的传动精度最高，传动误差最小。

假设所设置的多级圆柱直齿轮轮系总传动比为100，运用序列规划方法（SQP）求解目标函数（如式(11)所示）。最后结果得出最优级数为8级，每一级的传动比如表3所示。

表3 基于转动误差比各级传动比

传动级数是影响传动误差的一个因素，图4给出了多级圆柱直齿轮轮系传动级数n与转动误差比β的关系。

图4 传动级数n与转动误差比β的关系

由图4可以看出，其实传动比的级数n与转角误差β的关系其实并不是很大，没有明显的关系，由图可得当所设的传动级数在3级到50级进行变化时，目标函数β的变化量在很小，而且观察所求出来的传动级数在4左右，而由计算出来的结果可以知道，当轮系的总传动比为100，最优的级数确实为4级，也就是说在多级圆柱直齿轮轮系的总传动比为100的情况下，当传动级数为4级的时候，该轮系的传动误差比β达到最小，即轮系的传动精度最高。若想确定，其他大小的总的传动比下，最优的级数n，只需改变程序中的总的传动比大小，即可以求得该总传动比下最优的级数，而且代入求各级传动比的程序中，即可求出每一级的传动比大小。

2.5 传动级数和各级传动比与三个无因次变量的多目标优化

为了得到多级圆柱直齿轮轮系的传动级数n与轮系的转动惯量比J，体积比V，传动精度（用转动误差比β表征）三者结合的关系，可以建立轮系传动级数n与三者总目标函数F的关系，并且求得并分析二者的关系，进而求解出当多级轮系的传动级数为n时，使得目标函数F能达到最小值，则在该级数的情况下，该多级轮系的转动惯量比J最小，体积比V最小，传动装置的结构最为紧凑，而且多级轮系的传动误差β最小，轮系的传动的精度最高。

假设所设置的多级圆柱直齿齿轮轮系总传动比为I=100，运用序列规划方法（SQP）求解目标函数（如式(12)所示）。加权系数设置为：a1=0.5954；a2=0.1282；a3=0.2764。最后结果得出最优级数为5级，每一级的传动比如表4所示。

表4 基于多目标的各级传动比

传动级数与转动惯量比J，体积比V，传动精度β三者之间彼此影响。图5给出了传动级数n与总目标函数F的关系。

图5 传动级数n与总目标函数F的关系

由求解出的结果以及图5可以看出，在多级轮系的总传动比为一个定值的情况下，传动的级数n与目标函数F为一个类似于开口向上的抛物线，图形类似于单独分析转动惯量比J与传动级数n，单独分析体积比V与传动级数n的图像，由图5可以看出当传动级数小于5级时，目标函数随着级数的增加而减小，而当传动的级数大于5级时，目标函数会随着级数的增加而增加，当级数为5级时，目标函数达到最小值，所以最优的传动级数为5级，这与表4显示的结果一致，但综合考虑并对比与之前三个单独目标函数的分析结果，此总目数优化得到的最优级数更符合实际的情况，设计的传动的级数以及优化的结果是充分考虑转动惯量比小，结构较为紧凑，以及传动误差最小传动的精度最高的要求。这为传动装置轮系的优化提供了方便，在工程实践中有重要意义。综上可以得出，本文所构建的多级圆柱直齿轮传动比优化的数学模型准确性和有效性，优化出来的结果可以使多级圆柱直齿轮的转动惯量达到了最小，体积结构变得紧凑，传动误差变小，传动的精度大大提高。

3 结语

对于构建的多级圆柱直齿轮轮系传动比分配的数学模型进行分析，运用序列规划方法进行优化，当轮系的总传动比为一个定值的情况下，可以得到轮系的体积比V，转动惯量比J，相对于轮系的传动级数的图形为一条近似开口向上的抛物线，观察其最低点所对应的传动级数，即为最优级数。并且还可得出体积比V，转动惯量比J，以及转动误差比β三者共同构造的目标函数相对于传动级数的图像也近似为一条开口向上的抛物线，其最低点对应的级数即为最优级数，在该级数下，多级轮系的转动惯量最小，结构较为紧凑，并且传动的误差较小，传动的精度较高。相比于之前从单个目标进行分析，多目标优化结果更符合实际生产应用，故对生产实践提供了理论支撑。