基于干扰误差补偿的自动化电机自适应滑模反演控制

郭海全，刘 烨，周秋坤

（上海工程技术大学 电子电气工程学院，上海 201600）

0 引言

自动化设备通常是由多台单自由度电机组成的。采用大量辅助装置，一方面大大增加了电机体重、降低刚度[1]，另一方面，受到外界电磁干扰，电机运行控制系统遭受一定影响，无论是响应速度，还是动态性能都变得较差，严重时该系统直接影响整个电机的稳定性[2]。目前，对于电机自动化研究主要集中在电机设备配置、磁场分析及检测装置等方面，并在国内取得了一定研究成果[3]。然而，由于电机特殊的自动化机理，要想实现电机真正意义上的实用性能，需搭建合理的数学分析模型[4]。文献[5]提出一种电液位置伺服系统自适应反演滑模控制方法，利用自适应控制策略对系统建模，分析干扰误差，利用反演滑模控制算法设计位置控制器，完成伺服系统的精确控制；文献[6]提出基于混合网络的直流电机控制系统，组态设计分布式现场系统，将PLC分别设置成总控制器和现场端控制器，集成DP到I/O模块中，搭建基于混合网络的直流电机控制系统试验平台。

上述两种方法都是在钢体模型基础上展开研究的，该模型虽然在一定程度上降低了控制难度，但可靠性及电机运行真实性难以保证。因此，针对该问题，提出了基于干扰误差补偿的电机自动化自适应滑模反演控制方法。电机自动化自适应滑模反演结构控制作为一种有效控制方法，具有结构简单、鲁棒性强的优势，近几年被广泛应用于交流电机系统之中。通过电机动力学建模，据此设计电机干扰观测器，利用自适应滑模反演控制计算干扰误差，通过跟踪转子输出轴完成自动化电机自适应滑模反演控制。

1 自动化电机动力学建模

1.1 电机基本结构

自动化电机的基本结构如图1所示。

图1 实际自动化电机的基本结构

自动化电机主要是由定子球壳、转子球体两个部分组成的，采用实心结构，嵌有柱状钕铁硼永磁体加工的磁极。此外，在转子中心安装输出轴，以此实现转子的自由度运动[7]。自动化电机的特点是：磁极数目众多，能够提高转矩输出，同时通过磁体决定转子运动范围。

1.2 动力学建模

依据自动化电机基本结构，可知电机转子采用三维运动形式，该形式可以等效看作转子球心坐标轴独立旋转[8]。因此，应先确定坐标系（X，Y，Z），保持定子球壳位置不变，使转子球体与惯性主轴重合[9]。然后使用卡尔丹角（α，β，χ）将电机的转子动力学模型表示出来，卡尔丹角坐标变换如图2所示。

图2 卡尔丹角坐标变换

利用卡尔丹角坐标变换得出电机的动力学模型如下所示：

上述公式中：a=[α，β，χ]T表示卡尔丹角具体位置；表示角速度和角加速度；A（α）表示电机转子惯性矩阵；表示离心力矩阵；A1，A2表示坐标系下转动惯量；C表示施加在主轴上的控制力矩；Cf表示外界扰动[10]。

2 干扰误差补偿设计

研究自动化电机的干扰误差补偿，应根据电机的动力学模型设计干扰观测器，获取非线性干扰预测误差，根据观测器误差动态方程，得出干扰的不确定因素，并将其转化为电机相应的控制量。

设计的干扰观测器，其计算形式如式(4)所示：

式(4)中：λ（x1，x2）表示非线性函数；K（x1，x2）表示非线性预测增益；h表示不确定性干扰因素；f为电机输出值；W为重力加速度；λ为俯仰角速度[11]。

K（x1，x2）应满足：

依据上述公式，获取非线性干扰预测误差。正常情况下，相对于电机自动化动态特性受到的不确定性干扰变化是缓慢的，结合式(4)可得到观测器误差动态方程：

依据式(6)可知，K（x1，x2）＞0，此时可按照非线性预测的误差进行指数收敛。

非线性干扰预测的输出值传送给增益调整模块，并将预测的干扰不确定性因素转化为相应控制量[12]。

3 电机自适应滑模反演控制方案的实现

由于电机受到不确定性干扰因素影响，使得自动化电机自适应滑模反演效果较差。因此，应先使用干扰预测方法预测出电机的干扰，而未预测的部分干扰则使用滑模反演控制进行非线性补偿。

电机控制结构如图3所示。

图3 电机控制结构

电机设计的初衷就是转子输出轴能够实现从任意初始角度位置出发都能达到既定的轨迹运动形式，从控制方向来看，连续控制问题即是跟踪控制问题。因此，采用干扰误差补偿机制控制电机自动化滑模反演。

按照滑模反演理论，需定义电机的两个子误差分别是：

其中：e1、e2分别表示预测得到的干扰误差及未能预测的干扰误差，η1为虚拟控制量。

针对第一个误差，电机的虚拟控制量为：

针对第二个误差，电机动态公式为：

引入滑模切换函数，如下所示：

式(11)中：m为滑模面，由此获取控制力矩。

依据上述内容，设计的控制流程如图4所示。

图4 控制流程

具体控制方案为：

Step1：向自动化电子中输入既定轨迹，依据电机控制结构，结合两个误差以及滑模面函数，使电机达到最优的滑动模态。同时，通过设置自适应滑模面消除电机自身振动问题所带来的影响。

Step2：通过电磁参数及转子动力学惯性逆矩阵，改善外界扰动未知影响问题。

Step3：构造实际控制力矩阵，通过跟踪转子输出轴完成自动化电机自适应滑模反演控制。

4 仿真分析

为了验证基于干扰误差补偿的自动化电机自适应滑模反演控制方法的可行性，利用Simulink实现电机自适应滑模反演稳定控制，仿真平台如图5所示。

图5 仿真平台

在参考输入一种情况下，分别采用文献[5]方法和基于干扰误差补偿控制方法进行仿真实验。设置干扰信号为5sin(t)为时变信号，惯性平台仿真参数和控制器参数设置如表1、表2所示。

表1 惯性平台仿真参数

在突加外部干扰和突加信号干扰两种情况下仿真分析电机的控制性能。突加外部干扰控制仿真结果如图6所示。

表2 控制器参数

图6 突加外部干扰控制仿真结果

1）控制输入

在不同时间下，采用文献[5]方法与基于干扰误差补偿控制方法的控制输入值一致。

2）转角

在不同时间下，采用文献[5]方法与基于干扰误差补偿控制方法的转角值存在一定出入，最大相差0.001。

3）干扰

在时间为2t下，采用文献[5]方法的干扰值为2.8，而基于干扰误差补偿控制方法的干扰值为3.8，实际干扰值为3.75；在时间为4t下，采用文献[5]方法的干扰值为1，而基于干扰误差补偿控制方法的干扰值为-2.8，实际干扰值为-2.81；在时间为6t下，采用文献[5]方法的干扰值为0.9，而基于干扰误差补偿控制方法的干扰值为-1.7，实际干扰值为-1.71；在时间为8t下，采用文献[5]方法的干扰值为1.8，而基于干扰误差补偿控制方法的干扰值为0.8，实际干扰值为0.85；

综上所述：采用文献[5]方法会随着干扰具有明显波动趋势，而使用基于干扰误差补偿的控制方法，随着干扰没有明显波动情况。表明基于干扰误差补偿控制方法能够较好跟踪实际干扰信号变化轨迹，为干扰补偿提供帮助。

突加信号干扰控制仿真结果如图7所示。

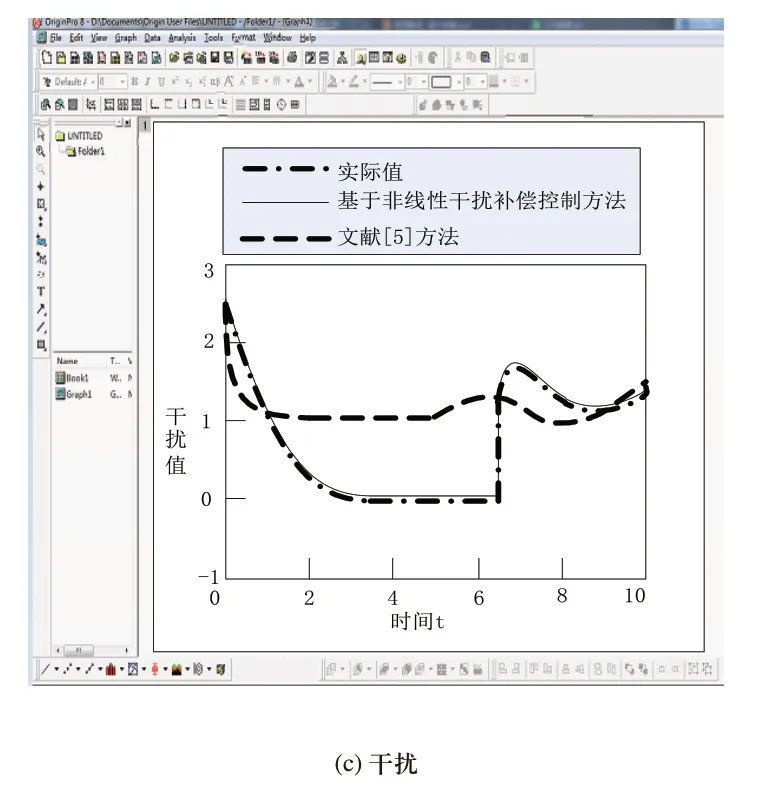
图7 突加信号干扰控制仿真结果

1）控制输入

文献[5]方法与基于干扰误差补偿控制方法的控制输入值基本一致。

2）转角

文献[5]方法转角波动小于基于干扰误差补偿控制方法的转角值。

3）干扰

在时间为2t下，采用文献[5]方法的干扰值为1.1，而基于干扰误差补偿控制方法的干扰值为0.3，实际干扰值为0.29；在时间为4t下，采用文献[5]方法的干扰值为1，而基于干扰误差补偿控制方法的干扰值为0.1，实际干扰值为0；在时间为6t下，采用文献[5]方法的干扰值为1.5，而基于干扰误差补偿控制方法的干扰值为0.1，实际干扰值为0；在时间为8t下，采用文献[5]方法的干扰值为1，而基于干扰误差补偿控制方法的干扰值为1.21，实际干扰值为1.2。

综上所述：基于干扰误差补偿控制方法在突加信号干扰情况下，也能较好跟踪实际干扰信号变化轨迹。

5 结语

结合自适应反演滑模算法对电机进行自动化控制，以此确定电机参数，同时控制滑模收敛性。在提出的基于干扰误差补偿的电机自适应滑模反演控制中，使用干扰误差补偿机制，使滑模误差在规定时间内收敛性达到最低。通过干扰误差补偿机制实现对干扰情况下控制效果的准确估计，避免外界干扰，使控制误差降到最低，以此提高电机抗干扰性能。实验表明该控制方法具有精准控制效果，在突加信号干扰情况下，也能较好跟踪实际干扰信号变化轨迹。

本文实验条件有限，未能对电机自动化长时间实际应用情况展开分析，因此，在今后研究进程中，以此为基础，进行该方面的研究。