圆弧树杈型压电能量收集器的设计与研究

宋 娟，刘琪才，陆颢瓒，杨佳慧，朱宇宬,王德波

(1.青岛黄海学院智能制造学院，山东青岛 266427；2.南京邮电大学电子与光学工程学院，江苏南京 210023)

0 引言

在振动能量收集领域中，压电式振动能量收集器作为一种较好的解决方案，有着结构简单、输出功率大、电能直接输出、发热较小、不受电磁干扰以及易于通过MEMS技术集成等诸多优点，目前成为振动能量收集领域应用较多、研究较多的一种能量收集方式[1-3]。现有的大多数能量收集器件均为基于线性几何构型设计的悬臂梁结构，但是单一悬臂梁能量收集器工作频带窄，输出电压低且受到激励方向的限制，针对上述存在的缺点，人们开发出了多种不同的悬臂梁结构以提高能量收集器的性能[4-6]。

Kasyap等设计了具有多种谐振频率的能量收集器结构，通过改变自由端质量块的大小实现多种谐振频率的线性悬臂梁组合构型[7]，或通过线性几何构型的尺寸变化来改变多阶谐振频率的间距[8]，进而实现不同频率宽带的压电振动能量收集器[9]；陈仁文等提出了褶皱型悬臂梁结构，利用曲面悬臂梁实现输出性能的提升；侯志伟提出了蒲公英状悬臂梁结构[10]，利用不同指向的线性悬臂梁构型实现不同方向的能量收集，当能量收集器的方向偏离最佳方向时，收集器的效率明显下降。上述新型结构虽然为提高压电式振动能量收集器性能提出了较为可行的解决方案，但实际应用中可能会面临诸多问题，尤其是线性几何构型的设计理念无法实现单一构型下多方向同频率振动能量的吸收，其效率方面也没有突破性的提高。

针对现有方案的不足，本文综合考虑工作频带、多方向效率和负载特性3个因素，提出了一种基于平面工艺集成的“圆弧树杈型压电式能量收集器”，并且建立了相应的器件阵子模型用于分析圆弧悬臂梁的受力情况。在非线性圆弧构型理论的基础上，建立多自由度系统理论，并通过测试分析器件的工作状态，检验该模型的稳定性，得到理论输出电压、输出功率、方向性效率以及耦合度大小，为下一代压电式振动能量收集器的设计提供新思路。

1 圆弧树杈型能量收集器的理论分析

1.1 圆弧树杈型悬压电能量收集器结构

圆弧树杈型压电式能量收集器结构如图1所示，整个结构通过固定梁、直形主梁，圆弧形副梁以及副梁上的质量块组成，其中每个副梁上的质量块的厚度不同，因此质量块的质量不同，以及每个副梁上的质量块距固定端的有效距离也不同，由此可以达到不同谐振频率的目的，本文所述的结构为一种演示结构，实际应用时可根据实际需求扩展副梁的数量。

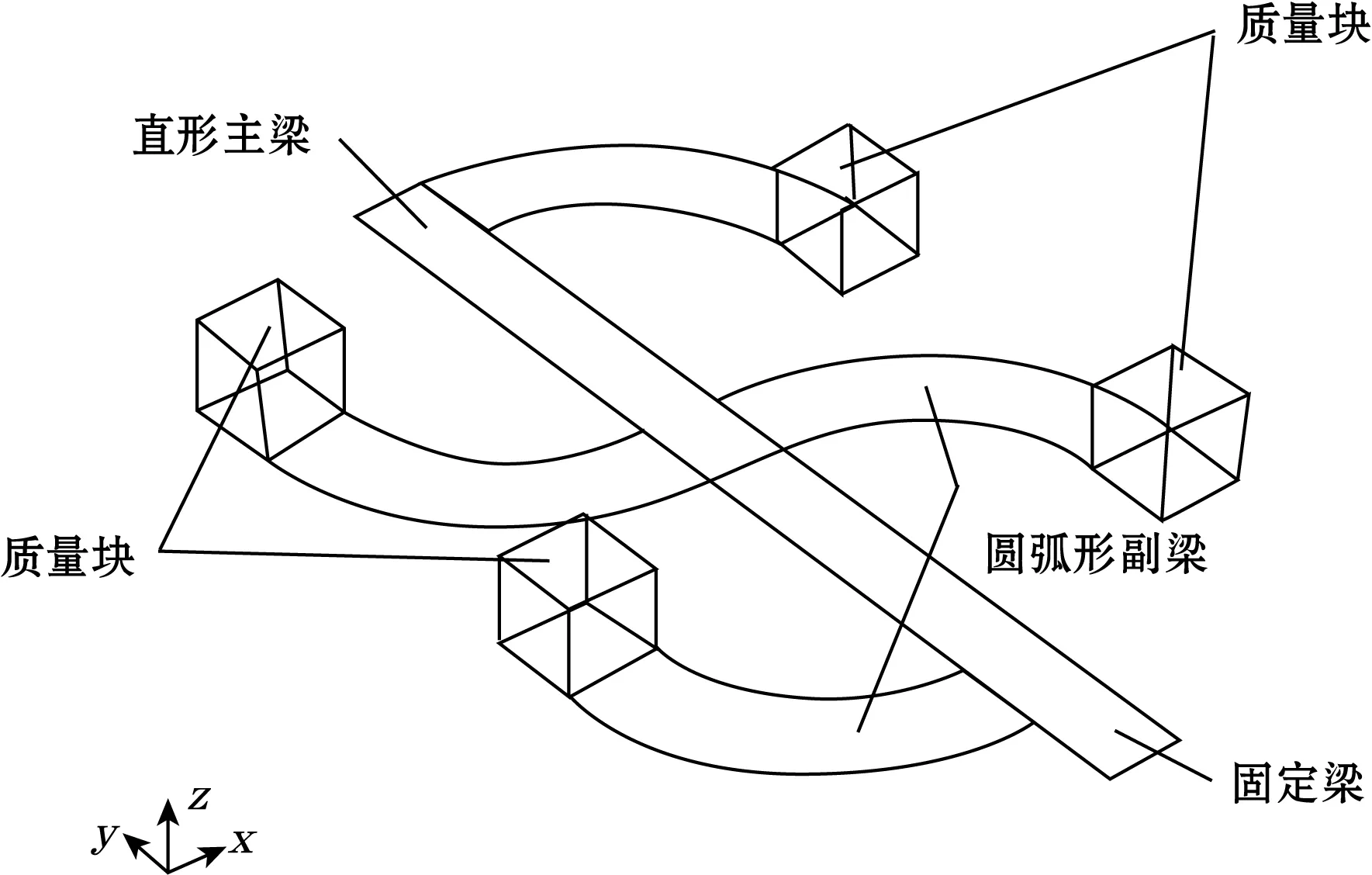
图1 圆弧树杈型压电式能量收集器结构

该结构通过4个质量块不同的圆弧悬臂梁实现4个相邻的谐振频率，从而提高器件的整体工作带宽，同时通过树杈的方式组合降低了器件占用面积，提高了面积使用率。在悬臂梁的设计上，基于非线性几何构型的设计理念，使用了新颖的圆弧梁设计，不同于常见的线性直型梁构型，只能利用弯矩产生的应力变化，圆弧梁在受到外部激励的作用下能同时产生弯矩和扭矩两种应力源，其中扭矩产生的应力变化远大于弯矩产生的应力变化，而压电式能量收集器的输出电能是与压电材料表面所受应力成正比的，因此基于圆弧梁的压电能量收集器能够产生更大的输出电压和输出功率。因此，圆弧梁能够有效吸收各个方向的激励，而常见的直形悬臂梁的最佳接收方向为梁平面的法方向，一旦激励偏离这一方向就无法有效产生弯矩，悬臂梁的形变、表面应力以及压电材料的电能输出将大幅度下降。

1.2 树杈型悬臂梁多阶频率

根据能量守恒理论，系统的动能和势能在任意时间之和为常数，即

(1)

式中：Ed为系统动能；Es为系统势能。

推广至树杈振动系统，树杈圆弧压电式能量收集器的动能和势能分别表示为[11]

(2)

式中：kz为直形主梁的等效弹性系数；kf为圆弧副梁的等效弹性系数；mz为直形主梁的等效质量；mf为圆弧副梁以及副梁上质量块的等效质量；rf为各圆弧副梁的振动偏移；rz为直形主梁的振动偏移。

由于直形主梁的几何构型呈线性，当发生自由振动时，固定端向载重端一方的截面应力分布均匀，所以线性构型下的振动偏移方程rz可近似等效为

rz=Acos(vt+φ)

(3)

式中：A为直形主梁的振幅；v为振动速度；φ为直形主梁与固定梁之间的相对转角。

将式(3)代入式(2)，可得树杈振动系统的自由振动方程[12]：

(4)

对式(4)进一步求解可得：

(5)

该行列式中线性主梁构型的弹性系数经化简得：

(6)

式中：d为直形主梁的长度；Tt为直形主梁弹性模量；Jl为直形主梁的惯性矩。

假定直形主梁的弹性系数kz理想状态下对各圆弧形副梁的振动影响相同，但实际中由于圆弧形副梁固定于直形主梁的位置存在差异，所以对各圆弧形副梁的振动影响不同。假定各圆弧形副梁间振动无耦合，各圆弧形副梁的弹性系数kf均可等效为单圆弧形压电能量收集器的弹性系数k0：

(7)

式中：b为质量块边长；l为圆弧副梁的弧中点半径；Ec为圆弧副梁弹性模量；Ic为圆弧副梁的惯性矩。

基于此，联立式(5)-式(7)可得到树杈系统在理想情况下前四阶谐振频率的值分别为

(8)

1.3 树杈型悬臂梁开路电压分析

由于圆弧梁的几何构型呈非线性，当发生自由振动时，固定端向载重端一方的截面应力分布不均匀，根据文献[13]的微分方程组和模态分析理论用于处理非线性圆弧副梁构型，可解得各圆弧形副梁的振动偏移为

(9)

式中：ρc1(x)为圆弧梁模态；υm为圆弧形树杈振动模型的多阶谐振频率；Cc各圆弧副梁的压电层间电容;Rl为层间电阻；Fo为外部激励；υn为系统的一阶固有频率；υo为外部激励频率；ζm为阻尼比。

由式(9)可得各圆弧形副梁的开路电压方程为

(10)

式中：Rd为负载电阻；χ为等效耦合系数。

1.4 建模与仿真

建立树杈圆弧形悬臂梁压电式能量收集器的模型，其器件结构参数如表1所示，材料参数如表2所示。

表1 圆弧树杈型压电能量收集器结构参数 mm

表2 能量收集器材料参数

利用Comsoltm有限元仿真软件，设定激励加速度1.1g(g为重力加速度)，设定频率取值在3～6 Hz，假设圆弧树杈型及单自由度能量收集器的振动方向为Z轴方向，通过改变作用在其上的振动频率，仿真结果如图2所示。

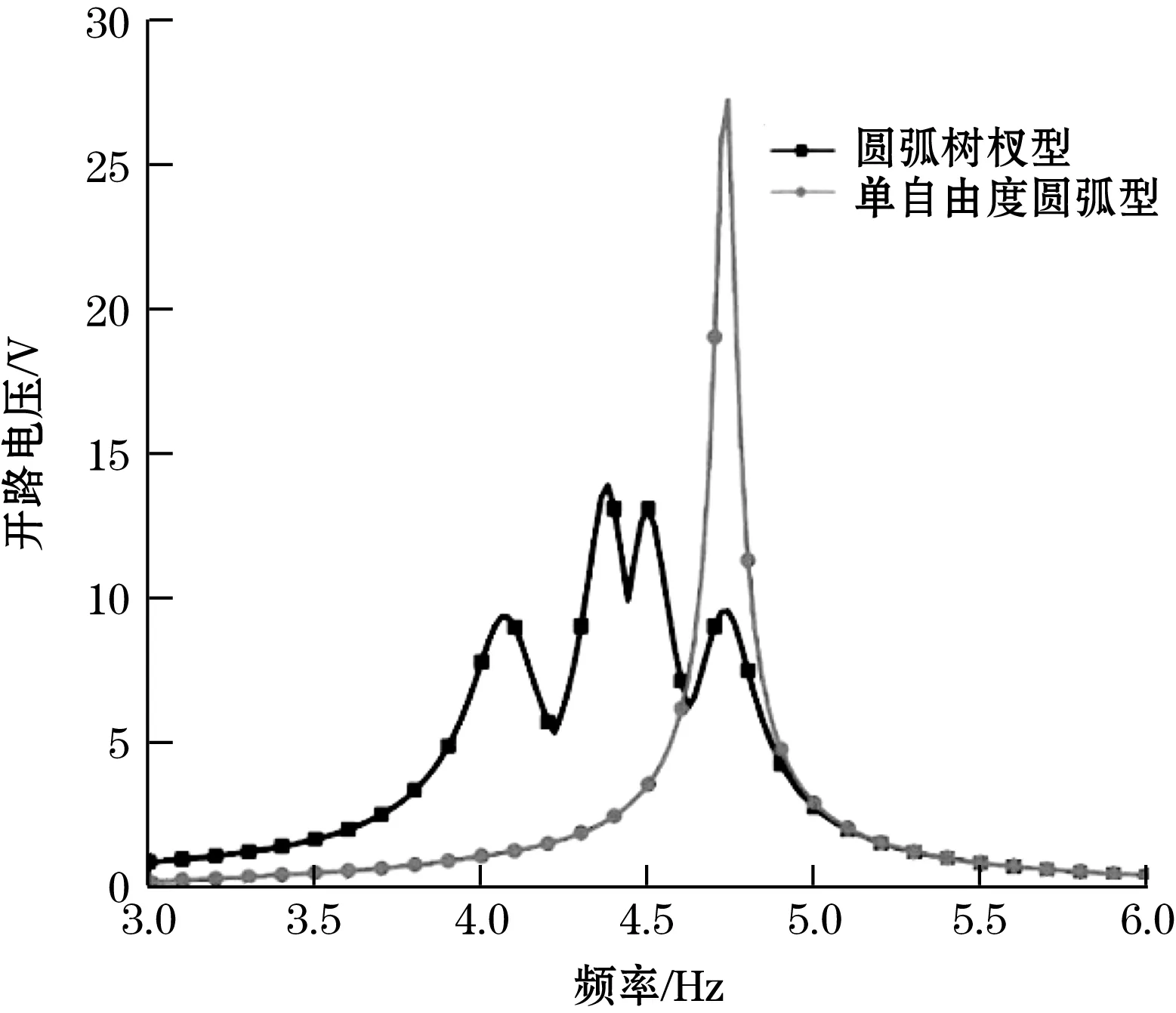
(a)X轴激励方向的理论频率响应

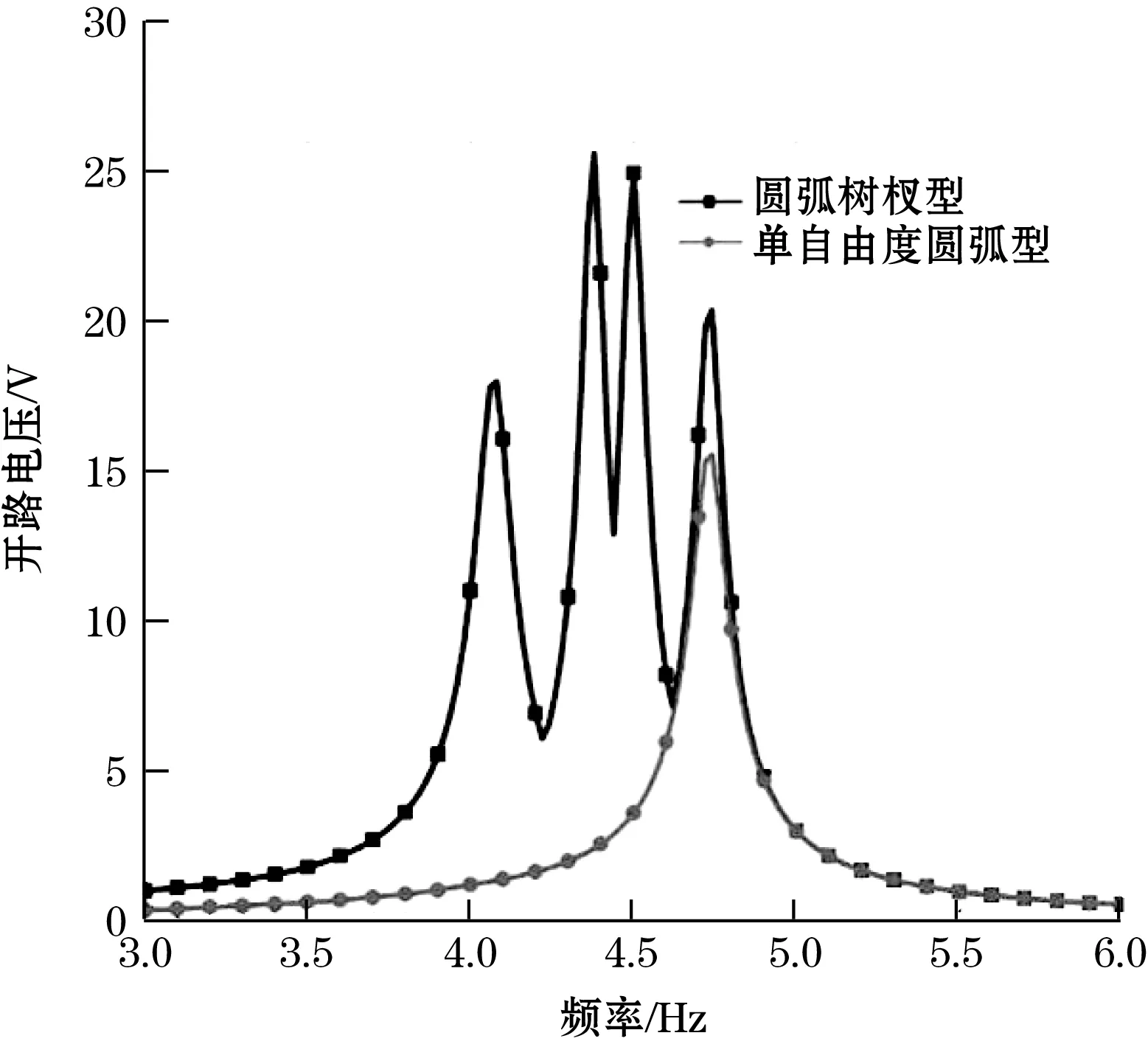
(b)Y轴激励方向的理论频率响应

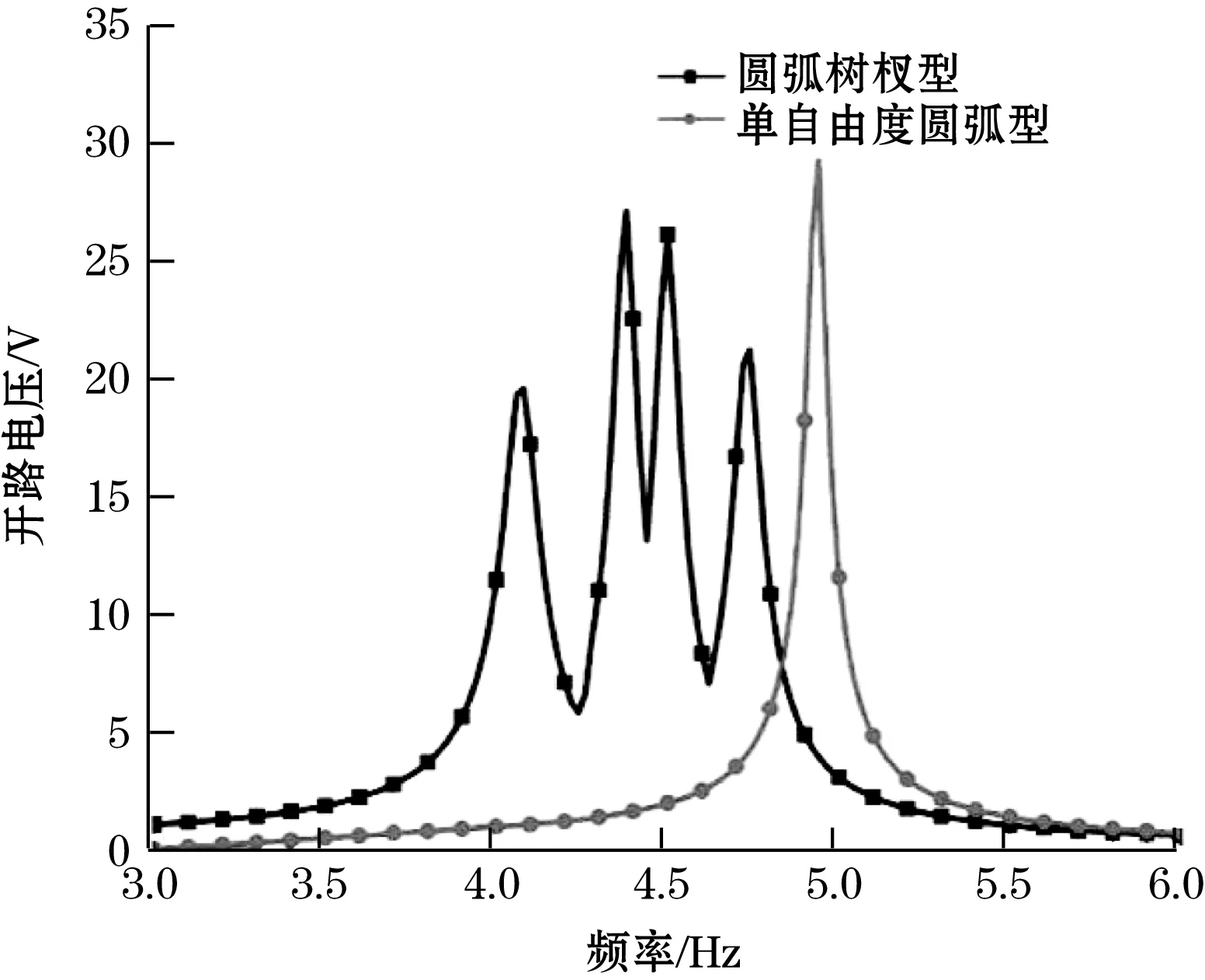
(c)Z轴激励方向的理论频率响应

单自由度与树杈型的谐振频率都与式(8)的理论谐振频率基本一致。根据仿真结果，树杈及单自由度圆弧形器件的谐振频率及对应开路电压如表3所示。

从表3可以看出：树杈圆弧形压电式能量收集器的四阶谐振频率分别为：4.08、4.38、4.50、4.74 Hz，对应的开路电压分别为：19.45、26.93、25.93、21.1 V。单自由度圆弧形器件的一阶谐振频率及开路电压为4.74 Hz和31.38 V。由于树杈型结构具有四阶谐振频率且在各方向上相差不大，较之于只有一阶谐振频率的单自由度结构显著提高了其工作频率，具有高宽带的优势。

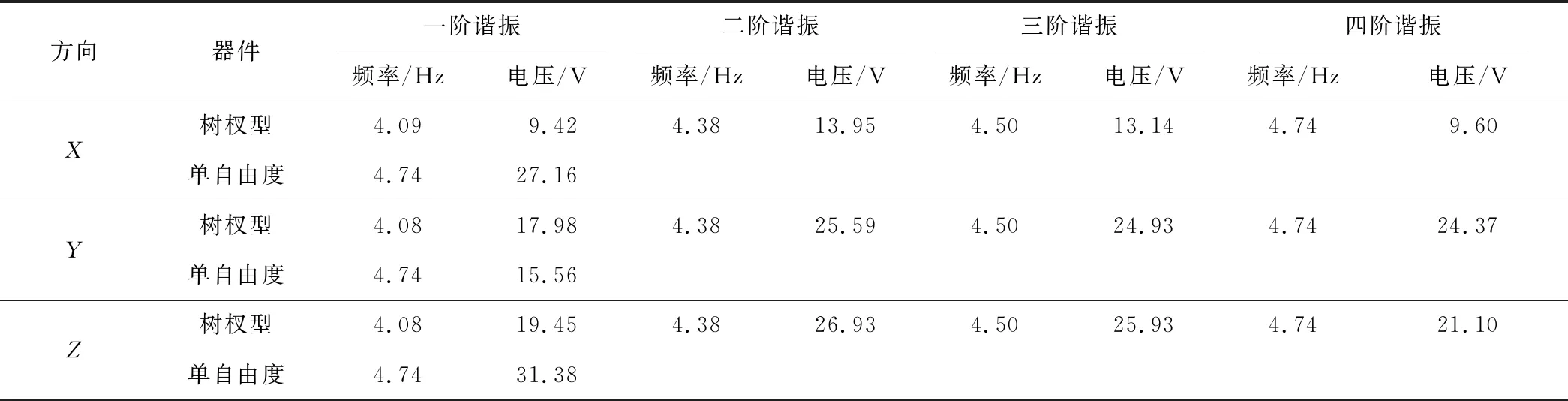
表3 圆弧树杈形压电能量收集器频率响应理论值

2 圆弧树杈型能量收集器实验测量

2.1 圆弧树杈型能量收集器频率响应测试

为验证圆弧树杈型压电式能量收集器具有宽频带特性，首先以Z振动方向为例，利用振动台控制振动频率变化进行扫频实验测量开路电压，获取能量收集器的频率响应测试值，由该模型的电压理论式(10)可得Z轴振动方向下两系统开路电压与频率的关系如图3所示。

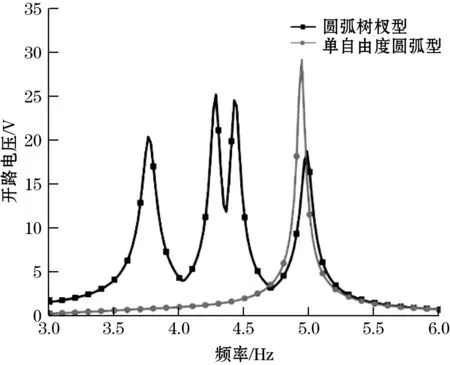
图3 Z轴方向下开路电压与频率关系图

由图2(a)可知单自由度圆弧型能量收集器的理论宽带为0.24 Hz，圆弧树杈型能量收集器的理论宽带为0.98 Hz，有效带宽扩展了0.74 Hz。根据图3及测试得到的数据可知：单自由度圆弧型能量收集器的测量宽带也是0.24 Hz，而圆弧树杈型的测量宽带为1.45 Hz，有效带宽扩大了1.21 Hz。对比实测与理论的频带宽度结果发现其存在一定的差异，造成这个差异的原因可能为理论模型采用的是无级间耦合时的理想情况，忽略了外力及阻尼的影响。而实际测试中圆弧悬臂梁在同一主梁上的振动将相互传递，从而使得其阻尼比之差减小，阻尼比的差异将导致实测的系统具有较宽的频带。

2.2 树杈及单自由度圆弧型能量收集器方向性对比

通过理论结果可知两圆弧形系统在X轴及Y轴方向仍有有效输出，为验证圆弧树杈型压电式能量收集器在不同方向激励下的效率，按照上述测试方法分别施加X轴、Y轴方向的振动激励以获得其频率响应，水平振动方向下开路电压与频率的关系如图4与图5所示。振动激励方向的变化不会影响各圆弧悬臂梁谐振频率的变化，即两圆弧形结构具备多方向同频率吸收能量的特点。分析两系统不同方向下的频率响应特性可知：同时激励方向为Z轴和Y轴时电能输出变化差异小，激励方向为X轴时电能输出有明显下降，但依旧有有效输出。因此，对比树杈型及单自由度圆弧型能量收集器的理论及实测数据，由于树杈型系统具有四阶谐振频率，提高了压电式能量收集器的宽带工作特性，但在Z轴和X轴激励方向下较之于单自由度圆弧型系统具有较低的开路电压输出。

图4 X轴方向下开路电压与频率关系图

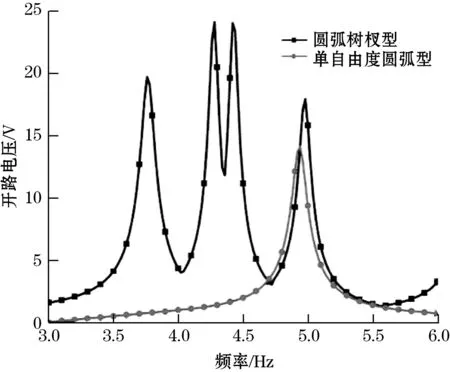
图5 Y轴方向下开路电压与频率关系图

3 结束语

本文通过对树杈型圆弧压电式能量收集器的设计，在单圆弧多方向压电能量收集理论的基础上建立了新的理论模型，并且分析了圆弧非线性构型在不同方向激励作用下的输出。该系统成功缩减了多阶频率间距，通过对理论模型的分析以及实验测试验证了树杈型圆弧压电式能量收集器在工作频带、输出电压、输出功率、方向效率上的诸多优点。实验结果表明：该能量收集器的四阶谐振频率差异小，相比于单圆弧压电能量收集器具有大宽带接收能力，同时相比于传统的直型悬臂梁可输出更高的电能；由于非线性构型较传统线性构型的优势，该模型各圆弧副梁均具备单一构型多方向振动能量吸收的优点。实际应用中可以通过增加圆弧副梁的方式进一步扩宽器件的工作频带，也能通过改变圆弧副梁的指向进一步改善器件整体的方向效率。