GP-周期势随机共振在无线电弱信号检测中的应用

杜太行，陈 霞，孙曙光，郝 静，王锐雄，梁 杰

(1.河北工业大学人工智能与数据科学学院，天津 300130；2.河北经贸大学信息技术学院，河北石家庄 050000；3.河北水利电力学院自动化与通信工程学院，河北沧州 061000)

0 引言

弱信号检测技术在故障诊断、无线电监测等领域应用广泛，实际环境中，由于电磁信号的复杂性，而且还伴随着噪声干扰，无线电信号在传播过程中，导致信号接收的不确定性，加之无线电信号频率很高，因此用常规的信号检测方法难以将它们检测出来并加以利用。因此，从嘈杂的背景中实现无线电弱信号检测既是研究的热点，也是广大学者研究的方向[1]。

由意大利学者R BENZI.等人研究古气象冰期周期性递归现象时提出的随机共振是一种与传统去噪方法不同的新方法[2]，将噪声变废为宝，与传统处理噪声的方法相比，让噪声、周期激励信号和随机共振非线性系统达到某种匹配，一定程度的噪声不仅不会给信号造成负面作用，还可显著增强随机共振系统的输出，增强弱信号的同时又削弱噪声信号，进而达到信号检测的目的。

目前为止，国内外学者对传统随机共振的模型对称反射四次势的研究已经较为成熟，学者们又发现其他势阱也能发生随机共振现象。文献[3]提出了周期势随机共振系统用来检测轴承故障。文献[4]对周期势系统中的共振进行了理论研究。文献[5]研究了布朗粒子受到谐波激励和有色噪声影响时的周期势系统。文献[6]利用周期势系统势函数作为随机共振的数学模型，其与传统随机共振系统相比具有更好的检测效果。文献[7]和文献[8]将Woods-Saxon势阱模型与径向Gaussian Potential势阱模型结合，分别检测叶片裂纹和轴承故障，与传统随机共振进行对比，目标频率处的频谱更清晰。

针对传统随机共振系统只能适用于小参数信号即低频(f≤1 Hz)周期信号的检测这一问题，学者们提出了频移变换[9]，归一化变换[10]，二次采样技术[11]，调节阻尼系数与频率相匹配的高频检测方法[12]。

基于以上基础，本文将周期势系统势阱与GP势阱结合提出一种GP-周期势随机共振系统，然后采用调节阻尼系数与频率相匹配的方法克服随机共振检测小参数信号的限制，来检测无线电弱信号，同时就检测效果与传统随机共振系统和周期势随机共振系统进行对比。

1 随机共振系统模型

1.1 传统随机共振

产生随机共振有3个条件必不可少：非线性系统，周期激励信号和噪声驱动。

传统随机共振系统的描述方程如下：

(1)

(2)

〈n(t)〉=0

(3)

〈n(t)n(t′)〉=2Dδ(t-t′)

(4)

将式(2)代入式(1)中，可得到描述传统随机共振系统的非线性Langevin方程为

(5)

式中：t为时间变量；x为系统响应；a和b为传统随机共振系统势函数的参数；k为随机共振系统阻尼系数；s(t)为输入的周期激励信号；D为噪声强度；n(t)为均值为0，方差为1的高斯白噪声；U(x)为传统随机共振系统的势函数；δ(t)为狄拉克函数。

1.2 Gaussian Potential(GP)势阱模型

在核物理学的研究中，一般用GP模型来描述复核散射[7]，径向GP模型可以表示为

(6)

式中：V为势阱深度；R为势阱宽度。

图1和图2表明了不同参数对GP势阱的影响。由图1所示，固定V，仅调节R改变的是GP势阱的宽度，并且随着R减小，势阱宽度也在逐渐变窄，势阱的两壁也逐渐变得陡峭，势阱的两端也越来越快地收敛于0。由图2所示，固定R，仅调节V改变的是GP势阱的深度，并且随着V减小，GP势阱的深度也逐渐变浅，并且势阱深度由V唯一决定。

图1 GP势阱结构参数R影响分析

图2 GP势阱结构参数V影响分析

1.3 周期势系统

周期势系统[6]的势函数Up(x)可表示为

Up(x)=-acos(bx)

(7)

式中：a,b为周期势系统的参数。

上述势阱也可描述为受到白噪声干扰的外部的扭矩的摆动。周期势系统势函数可描述为如图3所示。

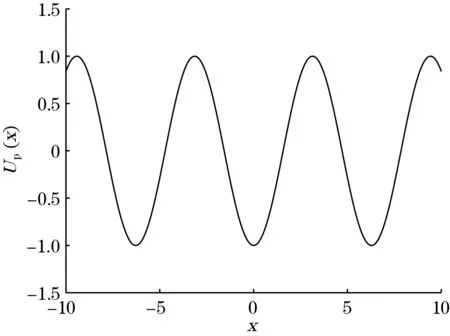
图3 周期势系统势函数

1.4 GP-周期势随机共振系统的势阱模型

基于以上GP势阱和周期势系统势阱，将GP势阱模型和周期势系统势阱模型相结合，提出一种GP-周期势随机共振系统模型，势函数如下：

(8)

根据复合函数求导法则对Ub(x)进行求导，得到GP-周期势随机共振系统的势阱力Ub′(x)为

(9)

将GP-周期势随机共振系统的势函数替代传统随机共振系统中的势函数，可以得到GP-周期势随机共振系统方程为

(10)

图4是GP-周期势随机共振系统的势函数图。该势阱让在单一的周期势系统势阱中振荡的布朗粒子的运动变成在2个势阱间进行跃迁的运动，可以提高噪声的利用率，从而改善输出频谱，使非线性系统、周期激励信号、噪声三者良好匹配，得到更好的随机共振效果，进而提高系统检测信号的性能。

图4 GP-周期势随机共振系统势函数

1.5 调节阻尼系数

源于绝热近似理论[13]和线性响应理论[14]的随机共振系统，只能适用于小参数信号即低频(f≤1 Hz)周期信号的检测，而无线电信号通常都是高频甚至超高频，因此，采用文献[12]调节阻尼系数与频率相匹配的方法，来打破传统随机共振检测小参数信号的限制，从而检测无线电信号。

由于随机共振系统隶属于非线性系统，目前对随机共振系统的非线性方程通常采用数值法求解，一般选用四阶龙格-库塔(Runge-Kutta)算法求解式(10)，如式(11)：

(11)

式中：h为步长；n为采样点。

2 仿真信号分析

为了说明上述GP-周期势随机共振系统的有效性，通过仿真信号进行验证，采用式(11)算法对随机共振系统非线性方程进行求解，同时对随机共振系统输出的信号进行频谱分析。

2.1 混合信号分析

首先构造了频率为10 MHz和30 MHz，噪声强度系数为D=0.6的无线电弱信号。sn(t)由无线电弱信号和高斯白噪声构成：

sn(t)=Asin(2πf1t)+Bsin(2πf2t)+n(t)

式中：A=B=0.3；f1为10 MHz；f2为30 MHz；n(t)为高斯白噪声。

将含噪信号分别输入GP-周期势随机共振系统、传统随机共振系统和周期势随机共振系统中。含噪信号经GP-周期势随机共振系统输出的频谱图如图5所示，和图6传统随机共振系统和图7周期势随机共振系统输出频谱相比有明显的2个谱峰并且波形平坦，杂频干扰少。

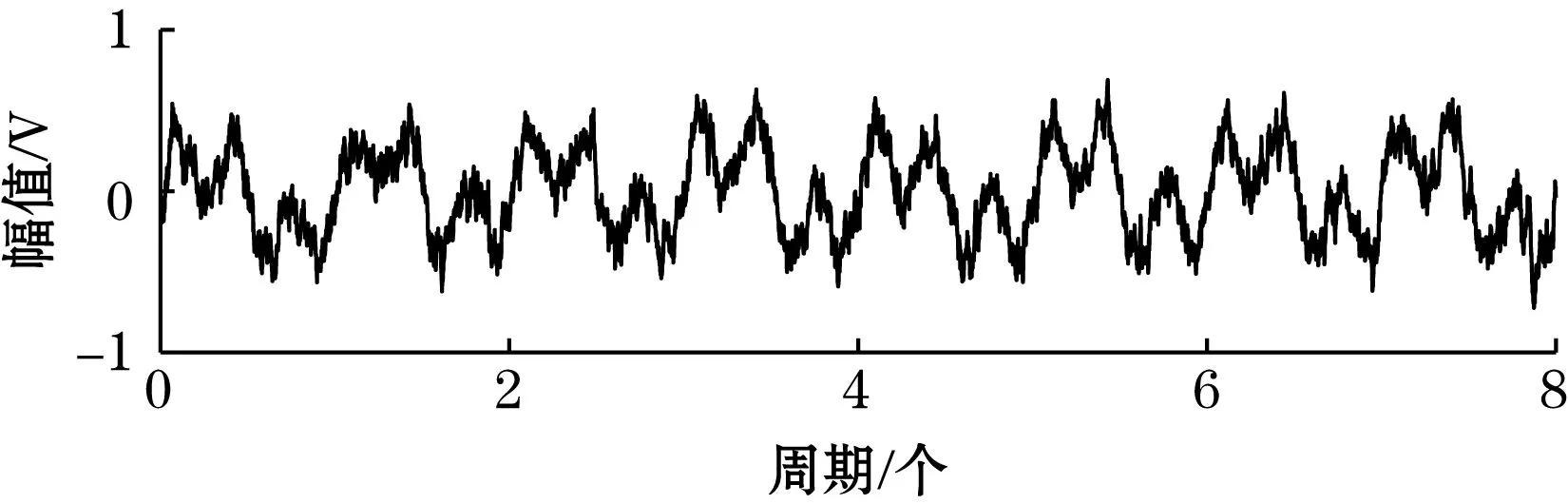
(a)系统输出信号时域图

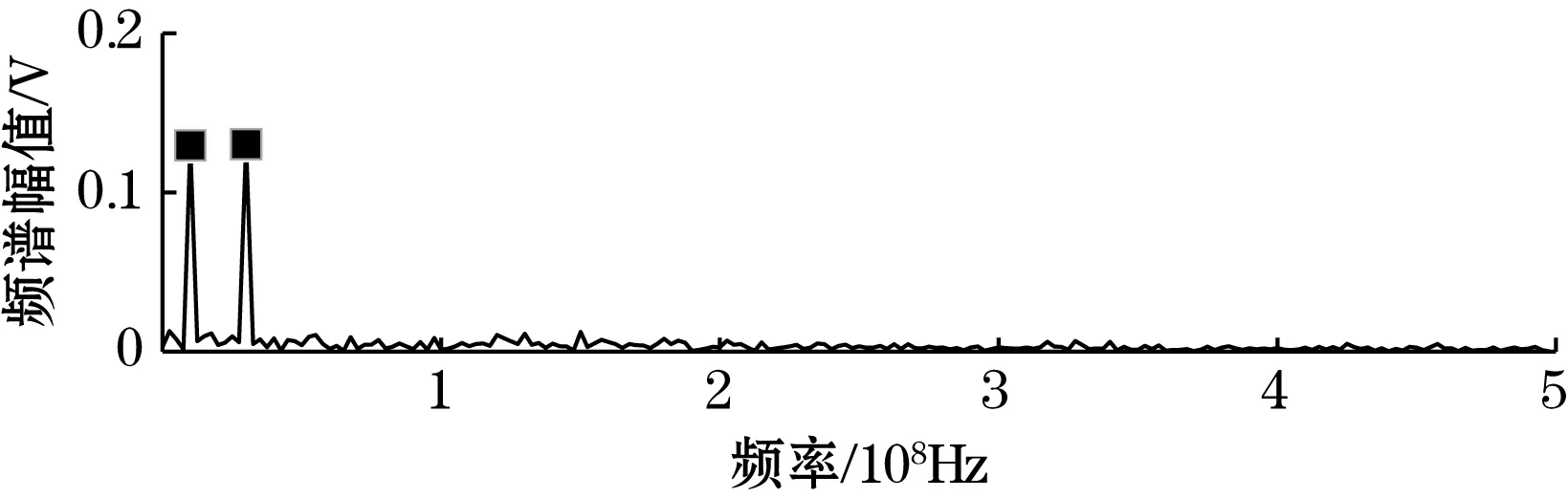
(b)系统输出信号频谱图图5 GP-周期势随机共振系统

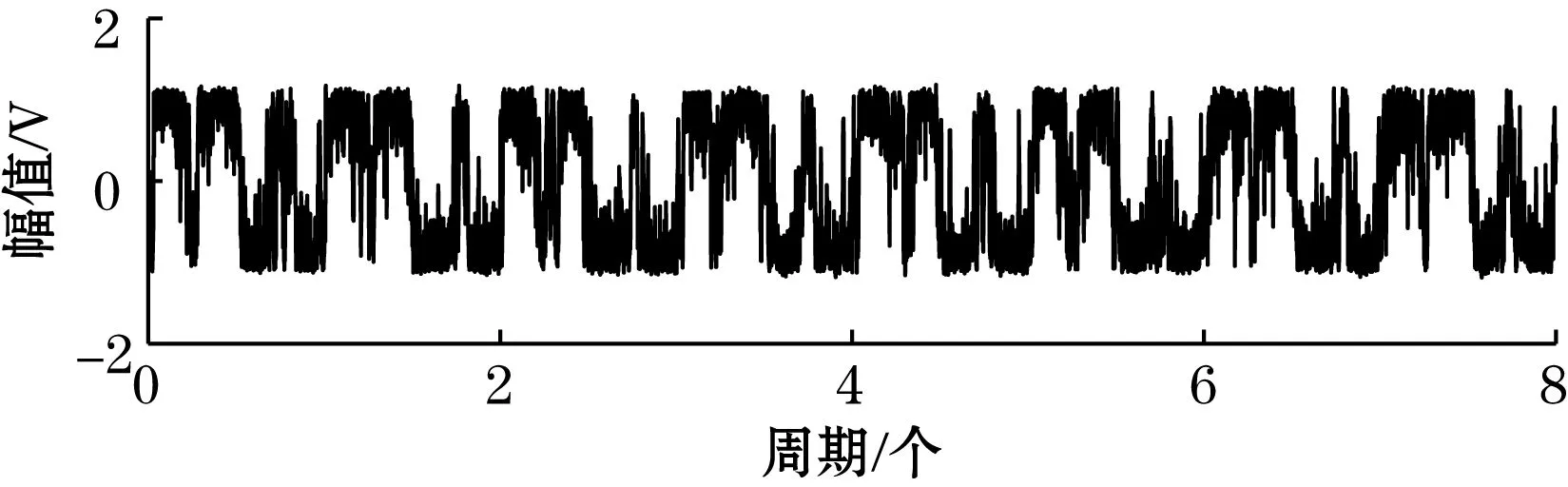
(a)系统输出信号时域图

(b)系统输出信号频谱图图6 传统随机共振系统

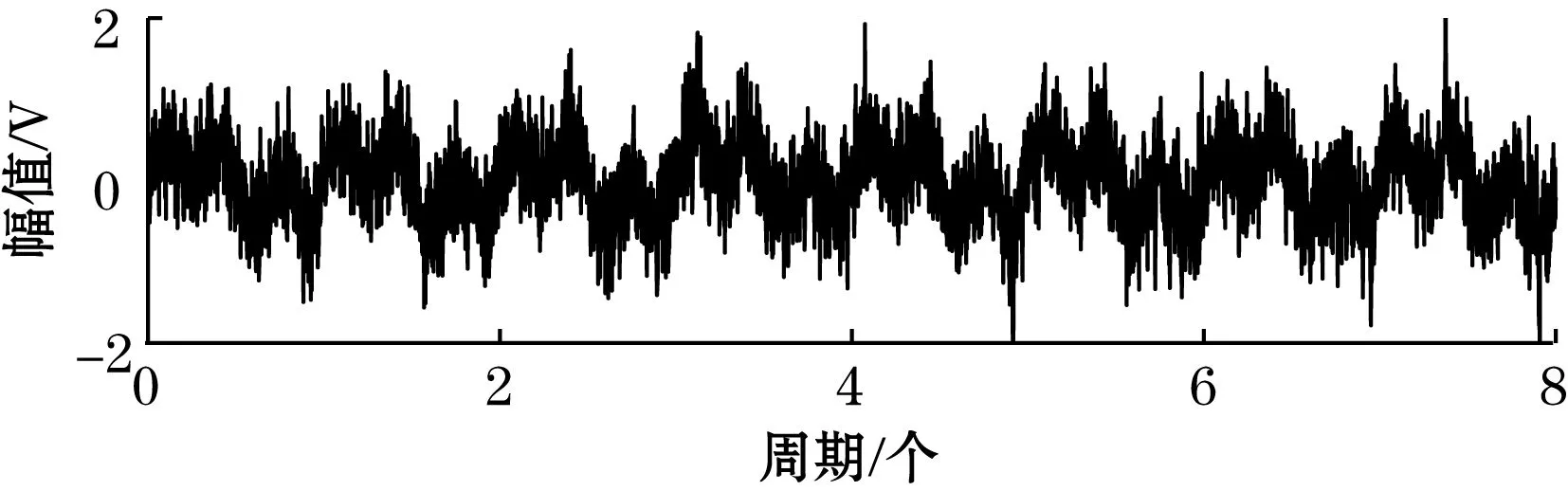
(a)系统输出信号时域图

(b)系统输出信号频谱图图7 周期势随机共振系统

随机共振系统检测信号的独特之处就是利用噪声，在非线性系统，周期激励信号和噪声共同的作用下，达到信号检测的目的。为了进一步说明GP-周期势随机共振系统对高斯噪声的利用率，通过在无线电弱信号中加入含噪更少的信噪比为50 dB的高斯白噪声进行验证，sn(t)由无线电弱信号和n(t)信噪比是50 dB的高斯白噪声构成。

sn(t)=Asin(2πf1t)+Bsin(2πf2t)+n(t)

式中：A=B=0.3；f1为10 MHz；f2为30 MHz。

如图8所示，含噪信号经GP-周期势随机共振系统输出的频谱，与图9所示传统随机共振系统输出频谱波形相比更为平坦，整个输出频段上的噪声几乎被滤除干净，并且与图10所示周期势随机共振系统输出频谱峰值相比约高0.05。由此可知，GP-周期势随机共振系统对噪声的利用率更高。

2.2 调制信号分析

无线电信号包括调制信号，下文对调制信号进行分析。采用阻尼系数与被调制信号频率fe相适应的原则。混合信号由无线电弱信号和高斯白噪声构成。

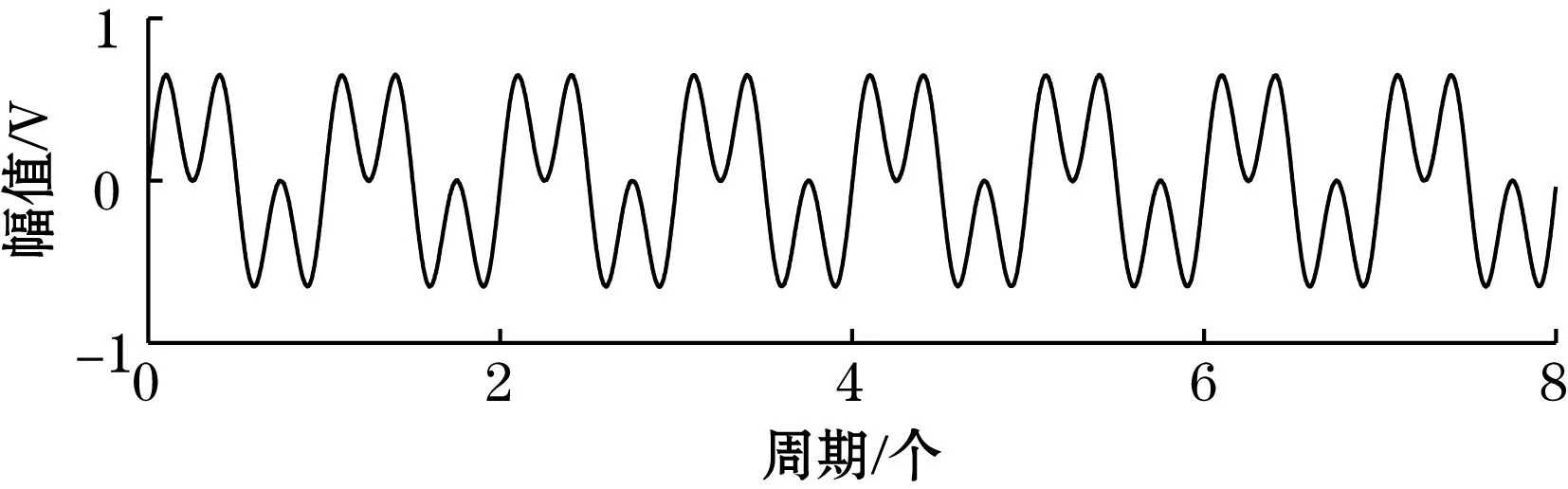
(a)系统输出信号时域图

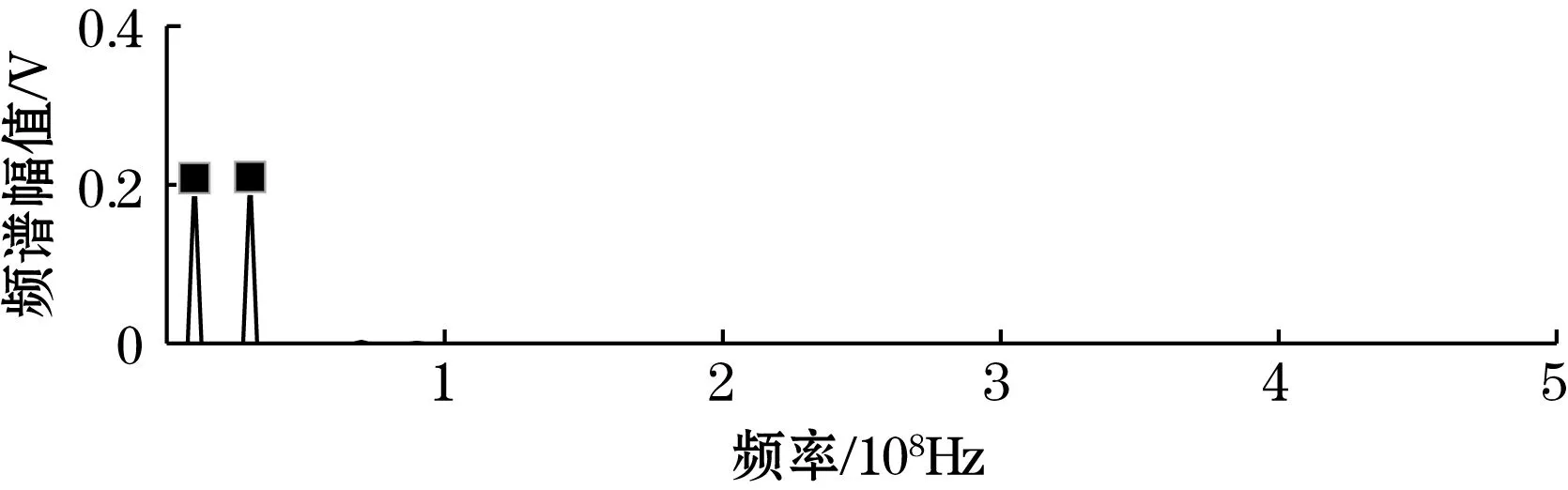
(b)系统输出信号频谱图图8 GP-周期势随机共振系统

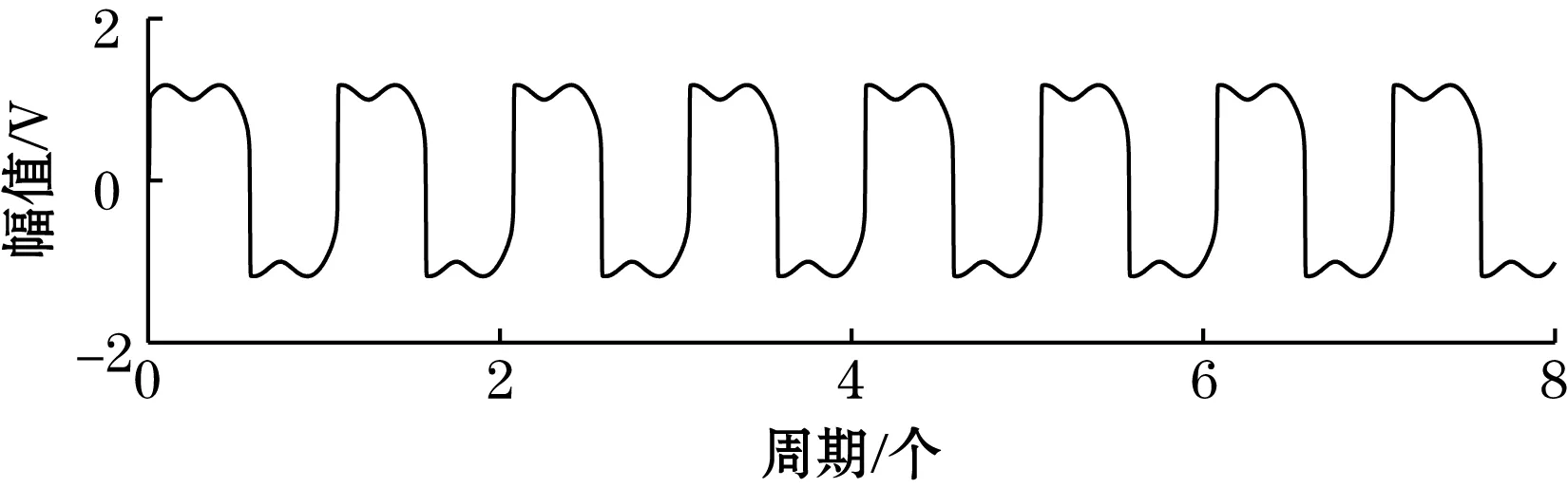
(a)系统输出信号时域图

(b)系统输出信号频谱图图9 传统随机共振系统

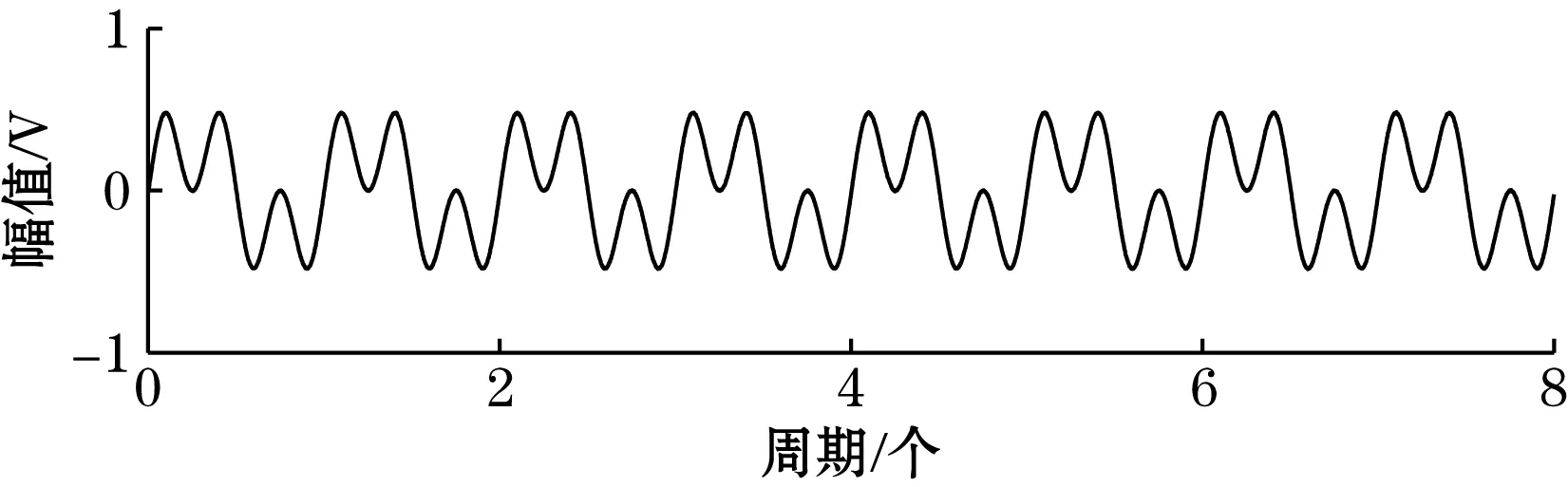
(a)系统输出信号时域图

(b)系统输出信号频谱图图10 周期势随机共振系统

式中：A=1；B=0.3；fc为调制频率，fc=1 500 Hz；fe为被调制频率，fe=60 Hz；D为噪声强度系数，D=0.6。

将无线电弱信号分别输入GP-周期势随机共振系统、传统随机共振系统和周期势随机共振系统中。含噪无线电弱信号经GP-周期势随机共振系统输出后如图11所示，清晰可见1 500 Hz的调制信号，并且在1 500 Hz前后的频谱波形都很平坦，噪声干扰少。经传统随机共振系统输出如图12所示，60 Hz的信号能被调制到1 500 Hz处，但是在频谱图中，明显看到频谱波形中1 000 Hz之前的信号频谱有明显的噪声干扰，“毛刺”较多，经周期势随机共振系统输出如图13所示，60 Hz被调制到1 500 Hz处，和图11相比，频谱平坦性较差。由此可知，GP-周期势随机共振系统对调制信号有良好的检测效果。

(a)系统输出信号时域图

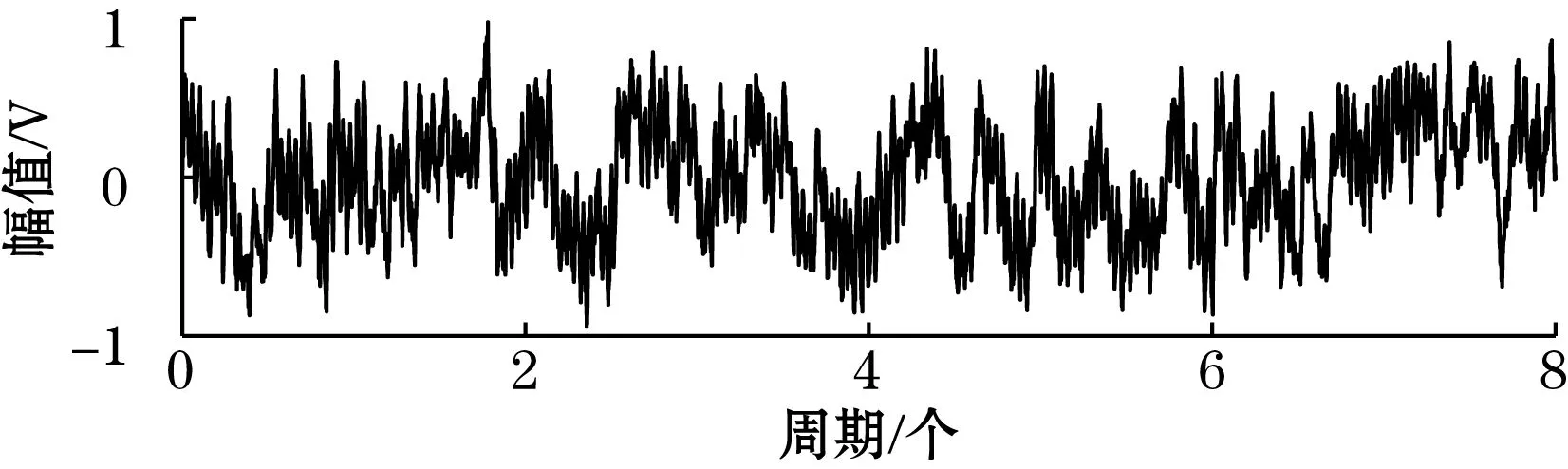
(a)系统输出信号时域图

(b)系统输出信号频谱图图12 传统随机共振系统

(a)系统输出信号时域图

(b)系统输出信号频谱图图13 周期势随机共振系统

3 结束语

本文将GP势阱模型与周期势系统势阱模型相结合，建立GP-周期势随机共振系统，并结合调节阻尼系数与频率相匹配的原则，检测高频和调制无线电弱信号。通过对高斯白噪声背景下的无线电弱信号检测，仿真结果表明，所提出的GP-周期势随机共振系统，与传统随机共振系统和周期势随机共振系统相比，减少了干扰频率成分的同时，突显了目标特征频率信号；同时增强了待测信号频谱幅值，提高了随机共振对噪声的利用率。表明GP-周期势随机共振系统检测无线电弱信号具有优势。