均质土微润灌湿润体模型构建及验证

范严伟，杨志伟，胡五龙

均质土微润灌湿润体模型构建及验证

范严伟1，杨志伟1，胡五龙2

（1. 兰州理工大学能源与动力工程学院，兰州 730050；2. 武汉理工大学理学院，武汉 430070）

为探明微润灌土壤湿润体运移的影响因素和变化规律，设置了56种微润灌情景（8种土壤质地、3种土壤基质势和10种微润管比流量的不同组合），利用HYDRUS-2D软件，模拟研究土壤饱和导水率、土壤基质势和微润管比流量对微润灌土壤湿润体的影响。综合考虑单位长度总渗水量、土壤饱和导水率、土壤基质势和微润管比流量等影响因素，基于量纲分析方法，建立了一种均质土微润灌湿润体尺寸估算模型，并利用数值模拟结果，定量获取了所建模型的待定参数，最后，采用试验资料评价了估算模型的可靠性。结果表明，土壤饱和导水率、土壤基质势和微润管比流量对微润灌土壤湿润体形状影响较小，且在湿润锋未到达地表前，湿润体形状均为以线源为轴线的近似“椭圆柱体”；相同土壤饱和导水率条件下，土壤湿润体水平、垂直向下和垂直向上方向上的湿润锋运移速率均随土壤基质势和微润管比流量增大而增大；当土壤基质势和微润管比流量恒定时，随土壤饱和导水率数值的增大，垂直向上和水平方向的湿润锋运移速率逐渐减小，而垂直向下的湿润锋运移速率存在先减小后增大的现象；所建模型的统计指标平均绝对误差、均方根误差均趋近于0，纳什效率接近1，说明模型估算效果良好，可为微润灌工程的运行及管理提供科学依据。

模型；土壤；湿润体；量纲分析；微润灌

0 引 言

微润灌是一种地下线源灌溉技术，其操作简单，工作水头低，对大田及温室作物具有较好的节水增产效果[1-2]。了解清楚不同影响因素下微润灌土壤湿润体的动态变化特征，进而构建湿润体特征模型，对设计经济高效的微润灌溉系统至关重要。

田间灌溉时，土壤湿润体的特性主要受土壤特性参数和灌水技术要素的影响。就土壤特性参数而言，土壤质地对湿润模式影响显著[3-4]，然而，即使是同一土壤质地，其容重不同，土壤内部的孔隙分布不同，土壤湿润体的运移速率也会有较大的差异，因此，灌溉参数不能仅视田间土壤质地状况而定；土壤饱和导水率受土壤质地、孔隙分布特征和容重的影响较大，同时在灌溉、排水系统工程的设计和土壤剖面中水通量的计算中起重要作用，所以，在确定灌溉参数时，可以考虑采用土壤饱和导水率来表征土壤质地、容重以及孔隙分布的差异。土壤特性参数还包括土壤基质势，根据土壤基质势制定灌溉方案是一种非常实用的方法[5-6]，因为其易于在各种田间条件下使用，无需对土壤类型或盐分水平进行校准，很多学者的研究表明，田间启动灌溉的土壤基质势适宜阈值大致在−50～−10 kPa之间[7-9]。从灌水技术要素考虑，微润管比流量与埋深是微灌系统较重要的2个参数。研究表明，相较于地下滴灌，微润管比流量更易受土壤质地、土壤容重、微润管埋深、压力水头、土壤初始含水率等因素影响[10-13]；埋深直接影响微润管周围土壤湿润体的水分分布位置，但对土壤湿润体的运移速率影响较小[11,14]。因此，在进行土壤湿润体运移距离的研究时，重点应考虑微润管比流量。

土壤湿润体特征值是灌溉计划制定和灌溉系统设计的重要依据，但田间灌溉时土壤湿润体难以直接观测，导致问题研究变得复杂。为此，国内外学者开发了一些解析模型[15-18]、数值模型[19-20]和经验模型[21-24]来描述湿润体运移过程。Kandelous等[25-27]对上述3类模型进行了分析与评价：解析模型较复杂，求解较困难；数值模型在已知土壤水力特性参数的前提下对湿润体的动态变化描述详细，但也存在模拟过程复杂和模拟参数难以获得等问题；经验模型形式简单，但大多数针对具体灌溉技术而建，其在不同灌溉模式下的普适性不强。量纲分析法能够合理恰当地选择特征尺度，将有量纲量转化为无量纲量，达到简化参数、量纲和谐的效果，为量化湿润体尺寸、解决湿润体不易观测的问题提供一种方便而实用的手段。

为探明微润灌土壤湿润体运移的影响因素及变化规律，采用HYDRUS-2 D软件，模拟研究土壤饱和导水率、土壤基质势以及微润管比流量对微润灌湿润体的影响；通过量纲分析法得到微润灌土壤水平向、垂直向上和垂直向下的湿润体尺寸与土壤饱和导水率、土壤基质势、微润管比流量以及单位长度总渗水量之间的关系，构建土壤湿润体尺寸的估算模型；采用试验数据验证预测模型的可靠性，为微润灌溉工程的设计和运行提供科学依据。

1 基于数值模拟方法分析湿润体运移影响因素

1.1 数值模拟

1.1.1 基本方程

假定微润管的渗水速率沿微润管方向呈均匀分布且土壤均匀和各向同性，微润灌土壤水分运动可近似为点源在垂直面上的二维运动，其土壤水流控制方程为二维Richards方程[28]，即

式中为垂向坐标，规定向下为正；为水平向坐标；为基质势，cm；为土壤体积含水率，cm3/cm3；为时间，min；()为土壤非饱和导水率，cm/min。

通过van Genuchten-Mualem (VG-M)模型描述式（1）中、()和三者之间的关系[29]。即

式中S为土壤相对饱和度，S=(−θ)/(θ−θ)；K为土壤饱和导水率，cm/min；θ和θ分别为土壤残余含水率和饱和含水率，cm3/cm3；和为经验常数，其中>1，=1−1/；为经验参数，cm-1；为经验系数，通常取0.5。

1.1.2 定解条件

图1为微润灌土壤水分运动模拟示意图。考虑田间微润管水平向铺设的对称性，模拟计算域的选取原则是，竖直向以微润管为起点的上至土壤表面、下至不受灌水影响的深度，水平向以微润管为起点向右至微润管间距的一半。

注：D是微润管埋深，cm；W是微润管间距，cm；Dd为模拟计算域深度，cm；Ψ为土壤基质势，cm；Ψ0为土壤初始基质势，cm。

模拟开始前，不同土壤类型的基质势均采用初始基质势。灌溉过程中，上边界与大气相接触，按大气边界设置；下边界在选取研究区域时不受灌水的影响，按自由边界设置；左边界为向下穿过微润管的中心线，右边界为相邻微润管中心线，均按零通量边界设置；单位长度微润管的出流量基本恒定[30-31]，按定流量边界设置。

1.1.3 模拟方案

为体现土壤类型的广泛性和研究成果的普适性，选取田间常见的8种土壤质地，其VG-M模型参数取自Carsel等[32]资料，土壤容重取自Pachepsky等[33]资料，具体见表1。

表1 8种典型土壤的VG-M模型参数

依据文献[7-9]，选取3种值（−100、−300和−500 cm）。参考文献[1,10-12,30]，压力水头取值范围为0.6～2.4 m，取值大致在10～40 cm之间。通过给定的、和，采用文献[34]中的比流量计算式确定模拟方案中的微润管比流量，模拟方案共计56种（8种土壤质地、3种土壤基质势和10种微润管比流量的不同组合），具体模拟方案见表2。

表2 模拟方案

1.1.4 求解方法

利用HYDRUS-2 D软件[35]进行数值求解时，考虑到田间实际和计算精度的要求，模拟区域设为D=100 cm，/2=60 cm的矩形区域，空间步长为1 cm，时间步长为0.1 min。求解时，对土壤剖面采用Galerkin有限元法进行空间离散，对时间采用隐式差分格式进行离散。

1.2 模拟分析湿润体运移影响因素

1.2.1 湿润体运移的影响因素

从56组模拟方案中，选取不同K、和影响因素组合下的7组单因素对比方案，绘制土壤湿润体运移变化图，如图2所示。

由图2可见，湿润锋未到达地表前，土壤湿润体形状差异较小，其轮廓线均为近似“椭圆柱体”；湿润锋到达地表后，微润管上部湿润体形状由“半椭圆”转化为“梯形”，微润管下部湿润体形状继续保持“半椭圆”。随灌水时间延长，湿润体向外逐渐扩展增大，但扩展速率逐渐减小。湿润体尺寸符合垂直向下>水平方向>垂直向上的规律。

注：纵坐标20 cm处为微润管所在位置。

1）土壤饱和导水率对湿润体运移的影响

图2a、2b和2c显示了不同K条件下湿润体随时间的变化规律。对比图2a、2b和2c，发现相同和条件下，随K的增大，同一时刻垂直向上和水平方向上的湿润锋运移距离逐渐减小。如持续微润灌24 h，K=0.007 5 cm/min土壤的垂直向上和水平湿润尺寸分别为12.0和12.3 cm，K=0.017 3 cm/min的土壤则减小为11.1和11.6 cm，而K=0.073 7 cm/min的土壤则再缩减为10.2和11.0 cm。相同和条件下，随K的增大，同一时刻垂直向下方向上的湿润锋运移距离表现出先减小后增大的现象。如持续微润灌48 h，3种K（0.007 5、0.017 3和0.073 7 cm/min）下的垂直向下湿润尺寸分别为12.7、12.0和13.2 cm。灌水结束时（132 h），3种K（0.007 5、0.017 3和0.073 7 cm/min）下的垂直向上的运移距离比垂直向下的运移距离分别下降35.5%，31.8%和38.1%；而水平方向的运移距离比垂直向下的运移距离分别下降6.5%，8.5%和28.9%。

2）土壤基质势对湿润体运移的影响

图2d、2f和2g给出了壤土在不同条件下湿润体的运移特性。对比图2d、2f和2g，发现相同K和条件下，3个方向上值越高，同一时刻湿润体运移距离越大，而且垂直向下方向上对湿润锋运移的影响更显著。如持续微润灌24 h，=−500 cm的3个方向（垂直向上、水平方向和垂直向下）湿润尺寸分别为11.5、12.0和12.5 cm，=−300 cm的增长为12.3、12.9和13.5 cm，而=−100 cm的再提升为13.3、15.0和17.0 cm。灌水结束时（132 h），3种值下垂直向上方向的湿润体运移距离均到达地表，水平方向，=−100和−300 cm的湿润体运移距离分别比=−500 cm的运移距离大31.0%，34.6%；而垂直向下方向，=−100和−300 cm的湿润体运移距离分别比=−500 cm的运移距离大7.5%，9.3%。

3）微润管比流量对湿润体运移的影响

对比分析3种条件下壤土湿润体运移过程（图2b、2d和2e）。可以看出，相同K和条件下，值越大，湿润体运移速度越快，同一时刻湿润体尺寸越大。如持续微润灌48 h，3种（0.010 7，0.014 5和0.018 2 mL/(cm·min)）下3个方向湿润尺寸分别为15.5、16.3、17.1 cm（垂直向上），17.1、18.1、19.2 cm（水平方向）和18.7、19.6、21.0 cm（垂直向下）。灌水结束时（132 h），3种下垂直向上方向的湿润体运移距离均到达地表，水平方向，微润管比流量为0.014 5和0.018 2 mL/(cm·min)的湿润体运移距离分别比0.010 7 mL/(cm·min)的运移距离增大11.2%和20.5%；而垂直向下方向，微润管比流量为0.014 5和0.018 2 mL/(cm·min)的湿润体运移距离分别比0.010 7 mL/(cm·min)的运移距离增大13.1%和23.7%。

1.2.2 湿润体运移轮廓

对图2进行分析，发现均质土条件下微润灌湿润体轮廓可分上下两部分，当上半部分在湿润边界未到达地表前，可用半椭圆形方程表示，如式（4）所示。

式中为水平向的最大湿润体尺寸，cm；为垂直向上或垂直向下的最大湿润体尺寸，cm；为湿润体轮廓上任意点的坐标。

由式（4）可知，湿润体的大小由水平向、垂直向上以及垂直向下的湿润体尺寸的最大值确定，基于此，建立3个方向上湿润体尺寸的估算模型则为确定湿润体大小的关键。

2 模型建立与评价

2.1 量纲分析

通过定性分析微润灌湿润体运移的影响因素，可知：K、和对微润灌土壤湿润体尺寸均有影响，另外，湿润体尺寸还受灌水时间的影响，故依据文献[21]将灌水时间对湿润体尺寸的影响用单位长度总渗水量（，mL/cm）代替。基于此，最终确定微润灌溉系统的水平向（）、垂直向上（1）以及垂直向下（2）的湿润尺寸取决于K、、以及。假设这些参数之间的关系为

式中表示参数之间存在某种关系。

式（5）中的7个参数根据量纲分析法及定理可得到5个独立的项，其之间的关系表示如下：

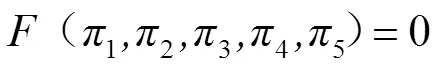
式中表示5个独立的项之间存在某种关系；1、2、3、4和5为由定理得到的无量纲量。

根据量纲和谐原理得到5个独立项的具体表达式，即

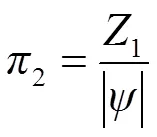
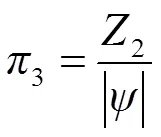
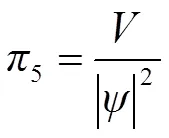
无量纲体积*、无量纲水平向湿润尺寸*、无量纲垂直向上湿润尺寸1*以及无量纲垂直向下湿润尺寸2*可由5个独立项的组合产生：

1）4与5的乘积得到无量纲体积*，表示如下：

2）1的平方与4的乘积得到无量纲水平向湿润尺寸*，表示如下：

3）2的平方与4的乘积得到无量纲垂直向上湿润尺寸1*，表示如下：

4）3的平方与4的乘积得到无量纲垂直向上湿润尺寸2*，表示如下：

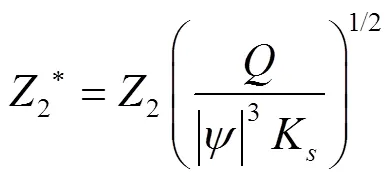
式（12）～式（15）所表示的无量纲参数之间的关系由文献[21]可得，即

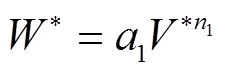
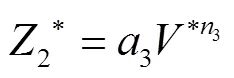
在式（16）～式（18）中，1、2和3是指数，1、2和3是系数。将W和V的值代入式（16）中获得式（19）：

同样地，将1*2*和*的值放在式（17）与式（18）中获得式（20）与式（21）：

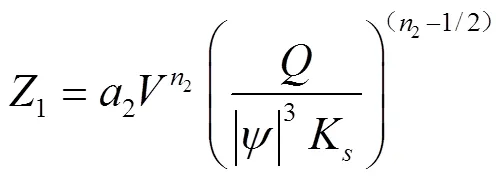
2.2 参数确定及模型构建

利用HYDRUS-2D软件的模拟结果及式（12）~式（15）计算无量纲项*1*2*和*，并借助Origin 9.0，采用式（16）～式（18）拟合获得参数1、2、3和1、2、3，如图3所示。其中，式（12）～式（15）与式（19）～式（21）中的微润管比流量（）为单位长度微润管的总出流量。

由图3可见，利用式（16）~式（18）拟合得到无量纲水平向湿润尺寸W、无量纲垂直向上湿润尺寸1以及无量纲垂直向下湿润尺寸2与无量纲体积*之间的关系，其指数1、2、3分别为0.53、0.53、0.56，常数1、2、3分别为2.91、2.65、4.88，拟合回归线的决定系数2分别为0.96、0.97、0.97，均接近1，说明拟合效果良好。将拟合获得的结果代入式（19）～式（21），得到不同K、、以及下的湿润体尺寸预测模型。即：

注：W*、Z1*、Z2*分别代表无量纲条件下水平方向、垂直向上和垂直向下湿润尺寸。

2.3 土箱试验

土箱试验用于模型的验证，供试土样分别取自甘肃省兰州市七里河区的粉壤土和武威市民勤县的砂黏壤土，且取土深度均为0～40 cm。土样经风干、碾压、过2 mm筛后待用。为获得均匀土壤剖面，试验前，土样按设定基质势加水并均匀混合，然后用塑料薄膜将土样密封，静置1 d，之后按设定好的容重分层（每层5 cm）装入土箱。装土完毕静置1 d开始试验，灌水时间设为3 d。土壤特性参数和灌水技术参数见表3。

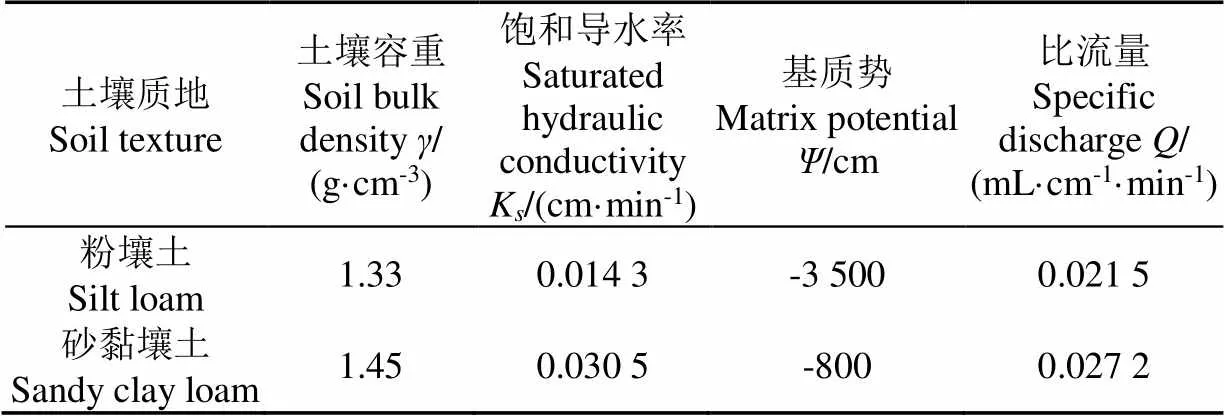
表3 供试土样特性参数和灌水技术参数

试验装置由土箱、高度可调节支架、橡胶管、马氏瓶和微润管组成（图4）。土箱由10 mm厚的有机玻璃制成，尺寸为60 cm（长）×60 cm（宽）×100 cm（高）。为防止土体内部气阻的发生，土箱底部留有多个通气孔（直径2 mm）。为便于观测湿润体形状与尺寸，装土时将微润管紧靠土箱壁，水平放置于设定的埋深处。试验中，马氏瓶在恒定水头下提供水量，马克笔绘制不同时刻湿润体轮廓。

2.4 误差分析

用平均绝对误差、均方根误差和纳什效率系数对模型的性能进行评价。如果比较结果显示平均绝对误差和均方根误差接近0，纳什效率系数接近1，则表明模型具有良好的模拟性能。统计参数使用以下方程计算[36]：

式中MAE、RMSE和NSE分别为平均绝对误差、均方根误差和纳什效率系数；O和C分别为第个实测值和第个计算值；为所有实测值的平均值；表示数据总个数。

注：H为供水面至土壤表面的压力水头，cm。

3 结果与分析

为进一步评价预测模型的准确性，利用室内土箱试验和已发表的有关微润灌湿润体运移的文献资料[12,30,37]中的实测数据对预测模型进行验证，并绘制实测值与预测模型计算值对比图（图5），且已发表文献资料中的土壤的相关基本性质见表4。采用式（25）～式（27）对计算值与实测值进行统计学分析（表4）。

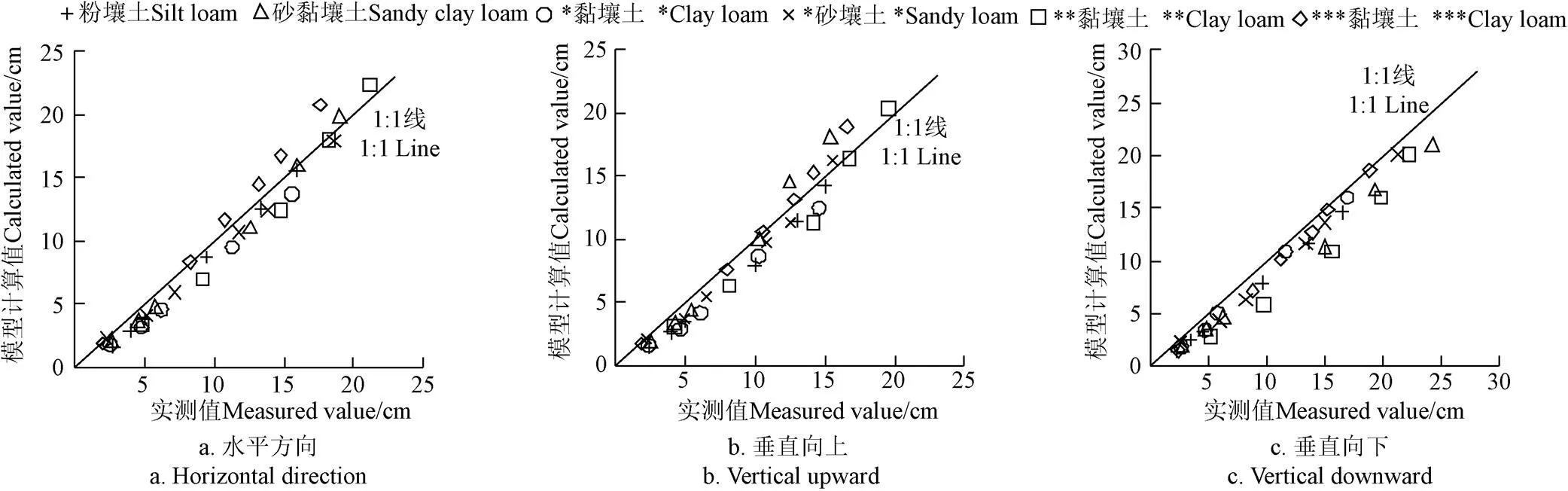
注：*表示取自文献[30]; **表示取自文献[12]；***表示取自文献[37]。

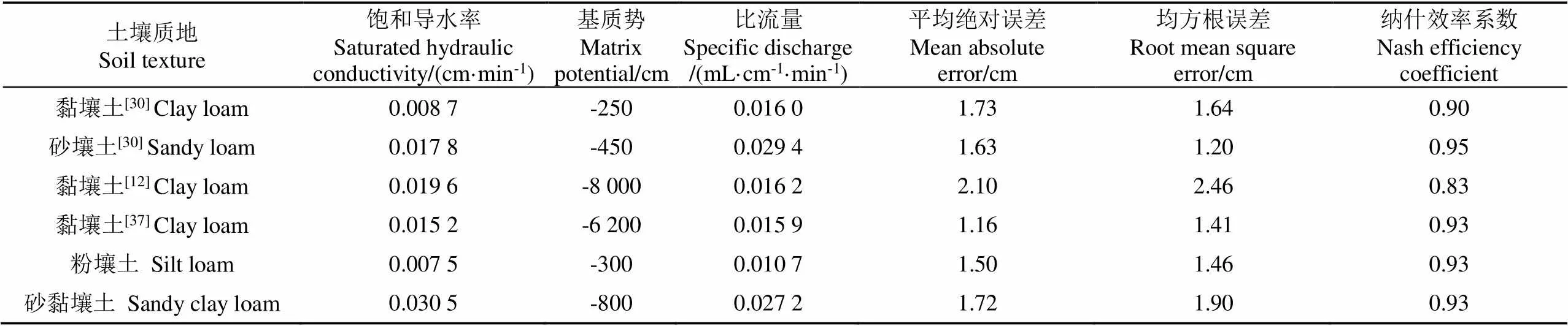
表4 湿润体运移距离实测值与模型计算值

由图5可见，以各土壤的水平、垂直向上以及垂直向下方向的湿润体运移距离的实测值与模型计算值为坐标的点均分布在1:1线附近，且利用检验计算得到各土壤在水平、垂直向上以及垂直向下方向的值均大于0.05，说明3个方向上各土壤的实测值与模型计算值均无显著性差异，一致性较好。借助指标MAE、RMSE和NSE对模型误差进行统计分析，如表4所示。由表4可知，MAE介于1.16～2.10 cm之间，RMSE介于1.20～2.46 cm之间，NSE介于0.83～0.95之间，模型预测效果良好。

4 讨 论

相同和条件下，水平和垂直向上的湿润锋运移距离随K的增大而减小，而垂直向下的湿润锋运移距离随K的增加存在先减小后增大的现象。分析原因可能是：1）相同和条件下，土壤饱和度随K的增大而减小，而饱和度越低，土壤的储水能力越强，湿润锋运移越慢[38-39]；2）相同和条件下，微润管处土壤基质势随K的增大而增大，而此处基质势越高，土壤水势梯度越大，湿润锋运移越快；3）相同和条件下，K越大，越有利于土壤水分运动。文中模拟情景融合了上述3种原因的影响，使K对土壤水分运动规律的影响变得较为复杂，后期仍需进一步定量研究其影响机理。

湿润锋运移距离随的增大而增大。究其原因为：1）相同K和条件下，越大，土壤初始越高，而初始越高，入渗开始前土壤孔隙所含水分越多，则土壤达到饱和状态时所需水分越少，所需时间越短[38]；2）土壤初始越大，()越大，水分在土壤中的运移速率越快[40]。湿润锋运移距离随的增大而增大。主要是越大，相同时间内进入土壤的水量越多，湿润锋运移越快。

灌水过程中，微润管内外水势梯度会影响微润管比流量，但作用时间较短，一般48 h后会保持稳定，这在牛文全等[13,41]的研究中得到验证。需要说明的是，微润灌作为一种地下续灌技术，可能会在植物整个生育期持续灌溉，土壤水分消耗问题是不可避免的，土壤水分消耗主要包括根系吸水消耗与土壤水分蒸发损失。因此，后期将结合根系吸水和土壤水分蒸发等对水分消耗开展研究，以期将湿润体大小保持在有效根区。

湿润体模型包含的土壤物理参数（土壤饱和导水率和土壤基质势）和灌溉技术参数（微润管比流量）容易测定，便于设计者针对不同土壤特性确定合理的灌水参数。需要说明的是，灌水推进过程中，湿润边界会达到地表，垂直向上的式（20）不再适用，但估算值大于微润管埋深时可取埋深值。湿润边界到达地表对水平向与垂直向下的湿润体运移影响不大，式（19）与式（21）依旧适用。

5 结 论

1）土壤饱和导水率、土壤基质势和微润管比流量对微润灌湿润体运移影响显著。3个方向（水平、垂直向上和垂直向下）湿润锋运移速率随基质势和比流量增大而增大；随饱和导水率的增大，水平和垂直向上的湿润锋运移速率逐渐减小，而垂直向下的湿润锋运移速率先减小后增大。

2）基于量纲分析法建立了一种均质土微润灌湿润体模型。采用试验数据进行验证，平均绝对误差介于1.16～2.10 cm之间，均方根误差介于1.20～2.46 cm之间，纳什效率系数介于0.83～0.95之间，所建模型估算效果良好，能够解决微润灌地下土壤湿润体难以观测的问题，为微润灌的工程设计和田间运行提供科学依据。

[1] 张明智，牛文全，路振广，等. 微润灌对作物产量及水分利用效率的影响[J]. 中国生态农业学报，2017，25(11)：1671-1683.

Zhang Mingzhi, Niu Wenquan, Lu Zhenguang, et al. Effect of moistube-irrigation on crop yield and water use efficiency[J]. Chinese Journal of Eco-Agriculture, 2017, 25(11): 1671-1683. (in Chinese with English abstract)

[2] Sun Q, Wang Y, Chen G, et al. Water use efficiency was improved at leaf and yield levels of tomato plants by continuous irrigation using semipermeable membrane[J]. Agricultural Water Management, 2018, 203: 430-437.

[3] 余小弟，刘小刚，朱益飞，等. 土壤质地和供水压力对竖插式微润管入渗的影响[J]. 排灌机械工程学报，2017，35(1)：71-79.

Yu Xiaodi, Liu Xiaogang, Zhu Yifei, et al. Effects of soil texture and water pressure on moistube infiltration in vertical inserting mode[J]. Journal of Drainage and Irrigation Machinery Engineering, 2017, 35(1): 71-79. (in Chinese with English abstract)

[4] Wang J J, Huang Y F, Long H Y, et al. Water and salt movement in different soil textures under various negative irrigating pressures[J]. Journal of Integrative Agriculture, 2016, 15(8): 1874-1882.

[5] Létourneau G, Caron J, Anderson L, et al. Matric potential-based irrigation management of field-grown strawberry: Effects on yield and water use efficiency[J]. Agricultural Water Management, 2015, 161: 102-113.

[6] 万书勤，闫振坤，康跃虎，等. 温室滴灌土壤基质势调控对番茄生长、品质和耗水的影响[J]. 灌溉排水学报，2019，38(7)：1-9.

Wan Shuqin, Yan Zhenkun, Kang Yuehu, et al. Response in growth, quality and water consumption of greenhouse tomato to change in matric potential at 20 cm below the emitter of drip irrigation [J]. Journal of Irrigation and Drainage, 2019, 38(7): 1-9. (in Chinese with English abstract)

[7] Klein I. Scheduling automatic irrigation by treshold-set soil matric potential increases irrigation efficiency while minimizing plant stress[J]. Acta Horticulturae, 2004, 664: 361-368.

[8] Liu H, Yang H, Zheng J, et al. Irrigation scheduling strategies based on soil matric potential on yield and fruit quality of mulched-drip irrigated chili pepper in Northwest China[J]. Agricultural Water Management, 2012, 115: 232-241.

[9] Contreras J I, Alonso F, Cánovas G, et al. Irrigation management of greenhouse zucchini with different soil matric potential level. Agronomic and environmental effects[J]. Agricultural Water Management, 2017, 183: 26-34.

[10] 张俊，牛文全，张琳琳，等. 初始含水率对微润灌溉线源入渗特征的影响[J]. 排灌机械工程学报，2014，32(1)：72-79.

Zhang Jun, Niu Wenquan, Zhang Linlin, et al. Effects of soil initial water content on line-source infiltration characteristic in moistube irrigation[J]. Journal of Drainage and Irrigation Machinery Engineering, 2014, 32(1): 72-79. (in Chinese with English abstract)

[11] 牛文全，张俊，张琳琳，等. 埋深与压力对微润灌湿润体水分运移的影响[J]. 农业机械学报，2013，44(12)：128-134.

Niu Wenquan, Zhang Jun, Zhang Linlin, et al. Effects of buried depth and pressure head on water movement of wetted soil during moistube-irrigation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(12): 128-134. (in Chinese with English abstract)

[12] 张国祥，申丽霞，郭云梅. 压力水头与土壤容重对微润灌溉水分入渗的影响[J]. 干旱地区农业研究，2017，35(4)：67-73.

Zhang Guoxiang, Shen Lixia, Guo Yunmei. Effect of pressure heads and soil bulk density on water infiltration under moistube irrigation[J]. Agricultural Research in the Arid Areas, 2017, 35(4): 67-73. (in Chinese with English abstract)

[13] 牛文全，张明智，许健，等. 微润管出流特性和流量预报方法研究[J]. 农业机械学报，2017，48(6)：217-224.

Niu Wenquan, Zhang Mingzhi, Xu Jian, et al. Prediction methods and characteristics of flow for moistube[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(6): 217-224. (in Chinese with English abstract)

[14] 范严伟，赵彤，白贵林，等. 水平微润灌湿润体HYDRUS-2D模拟及其影响因素分析[J]. 农业工程学报，2018，34(4)：115-124.

Fan Yanwei, Zhao Tong, Bai Guilin, et al. HYDRUS-2D simulation of soil wetting pattern with horizontal moistube-irrigation and analysis of its influencing factors[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(4): 115-124. (in Chinese with English abstract)

[15] Philip J R. Travel times from buried and surface infiltration point sources[J]. Water Resources Research, 1984, 20(7): 990-994.

[16] Chu S T. Green-Ampt analysis of wetting patterns for surface emitters[J]. Journal of Irrigation and Drainage Engineering, 1994, 120(2): 414-421.

[17] Cook F J, Thorburn P J, Fitch P, et al. WetUp: A software tool to display approximate wetting patterns from drippers[J]. Irrigation Science, 2003, 22(3/4): 129-134.

[18] Moncef H, Khemaies Z. An analytical approach to predict the moistened bulb volume beneath a surface point source[J]. Agricultural Water Management, 2016, 166: 123-129.

[19] Brandt A, Bresler E, Diner N, et al. Infiltration from a Trickle Source: I. Mathematical Models[J]. Soil Science Society of America Journal, 1971, 35(5): 683-689.

[20] Šimůnek J, van Genuchten M T, Šejna M. Development and applications of the HYDRUS and STANMOD software packages and related codes[J]. Vadose Zone Journal, 2008, 7(2): 587-600.

[21] Schwartzman M, Zur B. Emitter spacing and geometry of wetted soil volume[J]. Journal of Irrigation and Drainage Engineering, 1986, 112(3): 242-253.

[22] Malek K, Peters R T. Wetting pattern models for drip irrigation: New empirical model[J]. Journal of Irrigation and Drainage Engineering, 2011, 137(8): 530-536.

[23] Al-Ogaidi A A M, Wayayok A, Rowshon M K, et al. Wetting patterns estimation under drip irrigation systems using an enhanced empirical model[J]. Agricultural Water Management, 2016, 176: 203-213.

[24] 范严伟，邵晓霞，王英，等. 垂直线源灌土壤湿润体尺寸预测模型研究[J]. 农业机械学报，2018，49(10)：336-346.

Fan Yanwei, Shao Xiaoxia, Wang Ying, et al. Empirical model for predicting wetted soil dimensions under vertical line source irrigation[J].Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(10): 336-346. (in Chinese with English abstract)

[25] Kandelous M M, Simunek J. Comparison of numerical, analytical, and empirical models to estimate wetting patterns for surface and subsurface drip irrigation[J]. Irrigation Science, 2010, 28(5): 435-444.

[26] Subbaiah R. A review of models for predicting soil water dynamics during trickle irrigation[J]. Irrigation Science, 2013, 31(3): 225-258.

[27] Al-Ogaidi A A M, Wayayok A, Kamal M R, et al. Modelling soil wetting patterns under drip irrigation using HYDRUS-3D and comparison with empirical models[J]. Global Journal of Engineering and Technology Review, 2016, 1: 17-25.

[28] Richards L A. Capillary conduction of liquids through porous mediums[J]. Journal of Applied Physics, 1931, 1(5): 318-333.

[29] van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898.

[30] 张俊，牛文全，张琳琳，等. 微润灌溉线源入渗湿润体特性试验研究[J]. 中国水土保持科学，2012，10(6)：32-38.

Zhang Jun, Niu Wenquan, Zhang Linlin, et al. Experimental study on characters of wetted soil in moistube irrigation[J]. Science of Soil and Water Conservation, 2012, 10(6): 32-38. (in Chinese with English abstract)

[31] 张国祥，申丽霞，郭云梅. 微润灌溉条件下土壤质地对水分入渗的影响[J]. 灌溉排水学报，2016，35(7)：35-39.

Zhang Guoxiang, Shen Lixia, Guo Yunmei. Effect of soil structure on water infiltration under moistube irrigation[J]. Journal of Irrigation & Drainage, 2016, 35(7): 35-39. (in Chinese with English abstract)

[32] Carsel R F, Parrish R S. Developing joint probability distributions of soil water retention characteristics[J]. Water Resources Research, 1988, 24(5): 755-769.

[33] Pachepsky Y, Park Y. Saturated hydraulic conductivity of us soils grouped according to textural class and bulk density[J]. Soil Science Society of America Journal, 2015, 79(4): 1094-1100.

[34] Fan Y W, Huang N, Zhang J, et al. Simulation of soil wetting pattern of vertical moistube-irrigation[J]. Water, 2018, 10(5): 1-19.

[35] Šimůnek J, Šejna M, van Genuchten M T. The HYDRUS-2D Software Package for Simulating the Two-dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media: Version 2.0[M]. California: US Salinity Laboratory, Agricultural Research Service, US Department of Agriculture, 1999.

[36] Moriasi D N, Arnold J G, Liew M W V, et al. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations[J]. Transactions of the ASABE, 2007, 50(3): 885-900.

[37] 樊二东，王新坤，肖思强，等. 压力水头对微润灌溉土壤水分运移试验研究[J]. 排灌机械工程学报，2019，37(11)：986-992.

Fan Erdong, Wang Xinkun, Xiao Siqiang, et al. Experimental study of pressure head on water migration in soil under moistube-irrigation[J]. Journal of Drainage and Irrigation Machinery Engineering, 2019, 37(11): 986-992. (in Chinese with English abstract)

[38] 聂卫波，马孝义，王术礼. 沟灌入渗湿润体运移距离预测模型[J]. 农业工程学报，2009，25(5)：20-25.

Nie Weibo, Ma Xiaoyi, Wang Shuli. Forecast model for wetting front migration distance under furrow irrigation infiltration[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(5): 20-25.(in Chinese with English abstract)

[39] 曾辰，王全九，樊军. 初始含水率对土壤垂直线源入渗特征的影响[J]. 农业工程学报，2010，26(1)：24-30.

Zeng Chen, Wang Quanjiu, Fan Jun. Effect of initial water content on vertical line-source infiltration characteristics of soil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(1): 24-30. (in Chinese with English abstract)

[40] 王卫华，王全九，樊军. 原状土与扰动土导气率、导水率与含水率的关系[J]. 农业工程学报，2008，24(8)：25-29.

Wang Weihua, Wang Quanjiu, Fan Jun. Relationship between air permeability, water conductivity and water content for undisturbed and disturbed soils[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(8): 25-29.(in Chinese with English abstract)

[41] 张国祥，赵爱琴. “痕量灌溉”理论支撑与技术特点的质疑[J]. 农业工程学报，2015，31(6)：1-7.

Zhang Guoxiang, Zhao Aiqin. Query about theory and technical properties of trace quantity irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(6): 1-7. (in Chinese with English abstract)

Establishment and validation of wetting pattern model of moistube irrigation in homogeneous soil

Fan Yanwei1, Yang Zhiwei1, Hu Wulong2

(1.730050;2.430070)

Moistube irrigation is a kind of underground line source infiltration irrigation technology developed by using the principle of polymer semi permeable membrane. The growth and yield of crops are affected by the shape and size of soil wetting pattern but the wetting pattern is not easy to observe. Therefore, it is very important to understand the shape and size of wetting pattern for the design of economic and efficient moistube irrigation system. In order to facilitate users to quickly evaluate the moistube irrigation wetting pattern, a total of 56 moistube irrigation scenarios (different combinations of eight soil textures, three soil matrix potentials and ten specific discharges of moistube) were set up. By using HYDRUS-2D software, the dynamic changes of wetting pattern under different combinations of soil saturated hydraulic conductivity, soil matrix potential and specific discharge of moistube were simulated and analyzed. The results showed that before the soil wetting front reached the surface, there was little difference in the shape of the soil wetting pattern, and its contour was almost "elliptical cylinder"; after the wetting front reached the surface, the shape of the wetting pattern at the upper part of the moistube changed from "semi ellipse" to "trapezoid", and the shape of the wetting pattern at the lower part of the moistube kept "semi ellipse". In general, soil saturated hydraulic conductivity, soil matrix potential and specific discharge of moistube had little influence on the shape of the moistube irrigation soil wetting pattern; The size of moistube irrigation soil wetting pattern at the vertical downward was larger than that at the horizontal direction and vertical upward, and with the extension of irrigation time, the wetting pattern expanded outward gradually, but the expansion rate decreased gradually. Under the condition of homogeneous soil, the contour of moistube irrigation wetting pattern was divided into two parts: the upper part and the lower part. When the upper part of the wetting boundary did not reach the surface, it could be expressed by semi elliptic equation. Under the same soil matrix potential and specific discharge of moistube conditions, with the increase of soil saturated hydraulic conductivity, at the same time, the vertical upward and horizontal migration distance of the wet front gradually decreased, while the vertical downward migration distance of the wet front first decreased and then increased; Under the same soil saturated hydraulic conductivityand specific discharge of moistube conditions, there was a positive correlation between the migration distance of the wetting front and soil matrix potential in three directions. The higher the soil matrix potential value resulted in the greater the migration distance of the wetting pattern at the same time; Under the same soil saturated hydraulic conductivity and soil matrix potential conditions, the migration distance of wetting pattern was positively correlated with specific discharge of moistube. The larger the specific discharge of moistube value could result in the faster the migration speed of wetting pattern and the larger the size of wetting pattern at the same time. Generally speaking, soil saturated hydraulic conductivity, soil matrix potential and specific discharge of moistube had significant influence on the migration of wetting pattern in moistube irrigation. On this basis, taking into the influence factors such as the total water seepage per unit length, soil saturated hydraulic conductivity, soil matrix potential and specific discharge of moistube, and based on the dimensional analysis method, the estimation model for the wetting pattern of moistube irrigation of homogeneous soil was established, and the undetermined parameters of the model were obtained quantitatively by using the numerical simulation results. Finally, the reliability of the estimation model was evaluated by the test data. The mean absolute error was not more than 2.10 cm, the root mean square error was not more than 2.46 cm, and the Nash efficiency coefficient was not less than 0.83 of statistical index of the model. It showed that the measured value was consistent with the estimated value of the model, and the model estimation effect was well. It provides a scientific basis for the operation and management of moistube irrigation engineering.

models; soils; wetting pattern; dimensional analysis; moistube irrigation

范严伟，杨志伟，胡五龙. 均质土微润灌湿润体模型构建及验证[J]. 农业工程学报，2020，36(13)：83-91.doi：10.11975/j.issn.1002-6819.2020.13.010 http://www.tcsae.org

Fan Yanwei, Yang Zhiwei, Hu Wulong. Establishment and validation of wetting pattern model of moistube irrigation in homogeneous soil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(13): 83-91. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.13.010 http://www.tcsae.org

2020-03-25

2020-06-10

国家自然科学基金项目（51409137、51969013）；甘肃省科学基金项目（18JR3RA144）

范严伟，博士，副教授，主要从事水土资源利用和节水灌溉技术方面的研究。Email：fanyanwei24@163.com

10.11975/j.issn.1002-6819.2020.13.010

S274.3; S155.4+4

A

1002-6819(2020)-13-0083-09