基于无侧限抗压强度试验的土壤离散元参数标定

谢方平，吴正阳，王修善，刘大为，邬 备，张正中

基于无侧限抗压强度试验的土壤离散元参数标定

谢方平1,2，吴正阳1，王修善1,2，刘大为1,2，邬 备1,2，张正中1

（1.湖南农业大学机电工程学院，长沙 410128；2.智能农机装备湖南省重点实验室，长沙 410128）

为标定基于Edinburgh Elasto-Plastic Adhesion (EEPA)模型的土壤离散元参数，该研究通过单轴密闭压缩试验和无侧限抗压强度试验，以无侧限抗压强度σ为黏性指标，轴向应变ε为塑性指标，轴向压力-轴向应变曲线特征参数（，）为弹性指标，基于响应面标定了土壤离散元仿真参数。结合文献与实际情况确定参数试验范围，应用Plackett-Burman试验对7个初始参数进行筛选，发现塑性变行比λ和表面能Δ对黏塑性指标影响显著。根据试验结果，进行2次Central Composite试验，建立σ、ε与黏塑性参数的二次回归模型和σ、ε、、与弹性参数二次回归模型，并以实测值为目标优化求解，获得的优化参数组合为：塑性变形比为0.36、表面能为15.6 J/m2、恢复系数为0.37、静摩擦系数为0.6、滚动摩擦系数为0.26、黏性分支指数为4.24、切向刚度因子为0.52。最后将该参数组合下的仿真值与实测值进行对比验证，发现仿真ε和与实测值无显著差异，σ和与实测值存在较大差异。结果表明基于响应面法标定的EEPA模型参数可表征试验土壤的轴向塑性变形和3%～45%轴向应变内的应力-应变行为。

0 引 言

离散元法（Discrete Element Method，DEM）是一种将介质整体视为若干颗粒单元集合的数值模拟方法，利用牛顿第二定律和接触模型，以单个颗粒的运动学和动力学行为描述整体特征，被广泛用于谷物脱粒[1-2]与清选[3-5]、土壤与机具相互作用[6-10]等领域。研究对象外形各异、尺寸不一、粒度分布复杂、孔隙度不均匀，DEM模拟这些复杂的物理特性存在一定的误差，该误差会导致仿真对象的物理特性与实际情况存在较大差异[11-14]，为在DEM中再现研究对象的实际物理特性，需要确定合理的DEM参数以减小差异。因此，DEM参数的准确标定是成功仿真的关键，也是大部分离散元仿真的重要组成部分。近年来，DEM相关文献出版数量激增[15]，详细的DEM参数标定方法研究不断增多[16]。

在黏性介质的DEM参数标定研究中，一定固结应力条件下，无侧限抗压强度能直观地反映固结介质间的黏聚力水平[17-18]。土壤的无侧限抗压强度是指固结土壤在无侧限条件下，抵抗轴向压力的极限强度，是影响土壤抗破坏能力的重要指标[17]。土壤的无侧限抗压强度试验一般从单轴密闭压缩试验中获取固结试样。

Karkala等[17]在无侧限抗压强度仿真试验中，以100 mm/s的恒定速率（应变率=4 s-1）加载，直至试样失效；试验中记录压盘的压力和试样端面的变形，分析发现JKR表面能是无侧限抗压强度的极敏感参数，在JKR(Johnson-Kendall-Roberts, JKR）表面能参数的可行域内等分5组并逐一尝试，选择一组与实测值误差最小的JKR表面能参数作为标定结果。类似地，王宪良等[19]发现休止角、黏聚力和内摩擦角对颗粒半径、颗粒间静摩擦系数和滚动摩擦系数的敏感度都比其他参数高出一个数量级，利用响应面法得到这3项参考指标与3个主要参数的回归模型并优化求解得到最优的参数组合。Xia等[20]为模拟煤矿机械与煤矿之间的相互作用，根据黏性物料特性使用Johnson-Kendall-Roberts（JKR）模型，通过Plackett-Burman（PB）试验获得对休止角敏感的DEM参数，并将基于响应面法原理的Box-Behnken设计应用于标定。从已有文献发现，在多数离散元仿真研究中，仅对几个敏感参数进行标定是DEM参数标定常见的方法。其余未标定参数，如摩擦系数[21]、恢复系数[22]等，通常采用直接测量法确定，但JKR表面能、塑性变形比、粘结强度等参数难以通过直接测量法确定。

Coetzee[23]基于Hertze-Mindlin（no slip）模型以休止角为响应，对颗粒间摩擦系数进行标定。Ucgul等[24]将线性黏附内聚模型整合到线性Hysteretic Spring模型，并通过改变土壤静摩擦系数、滚动摩擦系数和恢复系数，获得与实际休止角和实测累计能量-贯入深度曲线相近的DEM参数。李俊伟等[25]以不同含水率的黑黏土为研究对象，基于JKR模型，通过休止角试验对颗粒间JKR表面能、静摩擦系数、滚动摩擦系数和恢复系数进行标定。Thakur等[26]首次提出Edinburgh Elasto-Plastic Adhesion (EEPA)接触模型，EEPA模型在Hertz接触理论的基础上，包含了颗粒塑性和黏性。Janda等[18]进一步证明EEPA模型适宜模拟黏重、可塑性强的农田土壤。基于JKR模型的黏弹性物料[17,25]、基于Hertze-Mindlin（no slip）模型的无黏性物料[14-16]和基于线性Hysteretic Spring模型的塑性变形物料[7,11,24]的DEM参数标定已有许多研究，而基于EEPA模型，对具备黏弹性的非线性塑性物料DEM参数标定鲜有报道。

Roessler等[16]认为，对于不同的应用，需要不同的标定试验，单独的宏观响应（例如堆积角）可能导致多个可行的参数组合，而多个参数组合可能无法用于单个响应以外的其他应用。本文以具有黏性且易产生塑性变形的土壤为研究对象，以轴向应变、无侧限抗压强度和压缩土壤时的非线性应力-应变特征为响应，通过Plackett-Burman和Central Composite试验进行EEPA模型的全部接触参数标定，并通过仿真与实测值进行对比验证，以期为基于EEPA模型的离散元仿真研究提供参数依据和可行的参数标定方法

1 材料与方法

本研究以单轴密闭压缩试验获得的固结土壤试样为材料，通过无侧限抗压强度试验，对EEPA模型参数进行标定。参数标定时，首先以恢复系数、静摩擦系数μ、滚动摩擦系数μ、表面能Δ、塑性变形比λ、黏结分支指数和切向刚度因子k为影响因素进行Plackett-Burman仿真试验，得到对轴向应变ε和无侧限抗压强度σ影响显著的因素，并以其为变量进行二次正交旋转组合仿真试验，得到ε和σ关于影响因素的回归方程，并以实测值为目标进行求解。在此基础上，以、μ、、k为影响因素进行4因素Central Composite仿真试验，得到4个影响因素对ε、σ和单轴密闭压缩阶段轴向压力-轴向应变曲线特征参数的方程组。在Design Expert 8.0.5软件中以实测的ε、σ和曲线特征参数为目标，对方程组求解，选择Desirability值最接近1(可靠度最高)的一组解。

1.1 土壤基本参数

利用圆孔筛筛分干土，取直径为2～3 mm的土壤颗粒。取样地点为湖南农业大学工程实训中心试验土槽，所用土壤来自湖南农业大学试验田，土质黏重、孔隙度大、可塑性强。为模拟土壤润湿过程，将土样放置于土槽内，喷洒适量水并覆盖地膜防止土样失水太快。放置12 h后进行含水率测定和后续试验，测定的试样含水率为26.25%。通过比重瓶试验测量土壤密度为2 670 kg/m3。由于可塑状态黏土的泊松比一般大于粉质黏土和沙土[8-10]，本文选取土壤泊松比为0.38。应力应变测试三轴剪切仪测量土壤剪切模量为1 MPa。

1.2 土壤物理特性参数

1.2.1 塑性和弹性指标

如图1所示，单轴密闭压缩试验时，内径40 mm、外径60 mm、高度150 mm的有机玻璃圆筒内壁涂抹适量润滑油，以减小限制壁与试样摩擦的影响。为便于后续取出试样进行无侧限抗压强度试验，将圆筒沿轴线均匀分割成2块并用抱箍固定。将240 g土样注入到圆筒中进行试验，万能力学试验装置以8 mm/s的恒定速率推动底部直径39 mm的压盘向下加载。加载至轴向压力为376.8 N（固结应力约为300 kPa）时以相同速率回车，直至完全卸载。使用线性EEPA模型达到300 kPa固结应力所用时间约为500 kPa所用时间的三分之一[18]，而非线性模型理论上将耗时更少，固结应力设置为300 kPa有利于节约仿真时长。

1.万能力学试验装置 2.压盘 3.抱箍 4.有机玻璃圆筒

利用试验获得土壤的轴向压力-轴向应变关系曲线（图2）表征土壤弹性。轴向压力-轴向应变拟合函数如下：

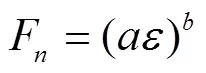
式中F是轴向压力，N；是试样的轴向应变，%；和是单轴密闭压缩阶段轴向压力-轴向应变曲线特征参数。

显然式（1）是经过原点的曲线，而万能力学试验装置以一定的入口力为起点采集数据，且加载初期，残余应变影响[27]导致式（1）与测量值的拟合程度不佳。因此，单轴密闭压缩期间试样的轴向压力-轴向应变曲线以固结应力为1 kPa即轴向压力约为1.256 N时的数据点为起点，将拟合曲线向左平移，使拟合曲线通过（0，1.256），为此，将式（1）调整为：

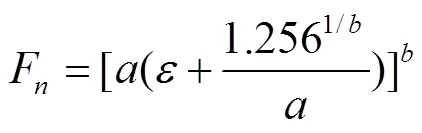
由于实际轴向压力-轴向应变曲线在45%的应变以后与仿真曲线有较大差别，残余应变约为轴向应变的0%～3%，所以式（2）仅拟合实测试验中加载阶段3.0%～45%的轴向应变。

利用试验后固结试样发生的轴向应变ε表征土壤塑性。ε定义为

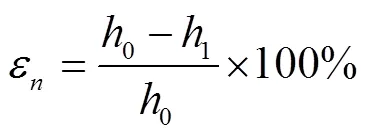
式中0是单轴密闭压缩试验中试样的初始高度，mm；1是到达预设固结应力并完全卸载后试样的高度，mm。

测量塑性指标时，将单轴密闭压缩期间轴向压力为1.2 N（固结应力约为1 kPa）时的试样高度记为0，完全卸载后的试样高度记为1，依据式（3）计算ε。测量弹性指标时，依据式（2）拟合3.0%～45%轴向应变的轴向压力-轴向应变数据，并根据式（2）求解曲线特征参数和。

试验重复3次，结果为：为0.038、0.039、0.046；为3.667、3.782、3.702；ε为36.19%、37.22%、34.17%。取平均值有：=0.041，=3.717，ε=35.86%。

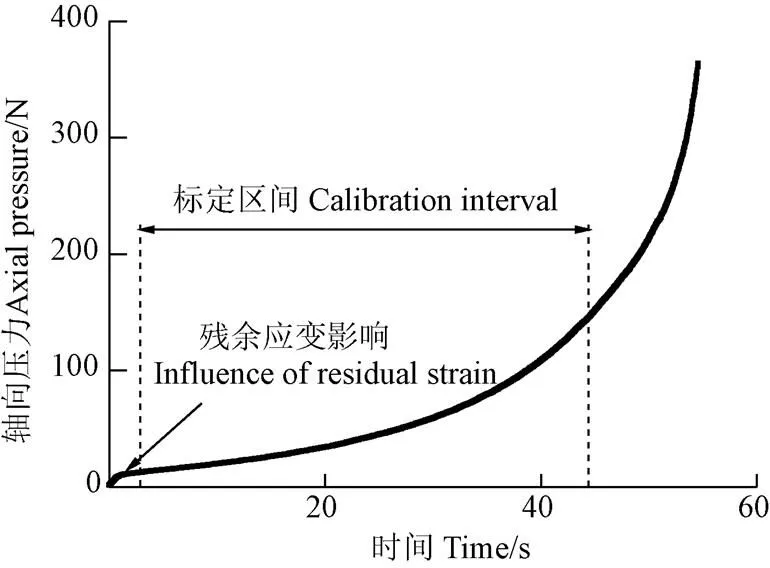
图2 单轴密闭压缩压力曲线

1.2.2 土壤黏性指标

利用无侧限抗压强度试验测量土壤无侧限抗压强度σ，试验如图3所示。

1.万能力学试验装置 2.压盘 3.失效试样

σ定义为

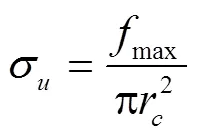
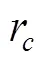
试验时，利用切土刀将单轴密闭压缩试验结束后的试样高度切削至81 mm。修整试样端面至平整，最后试样高度约为80 mm，进行无侧限抗压强度试验。万能力学试验机以3.2 mm/s的恒定速率推动底部直径为100 mm的压盘向下加载，直至时间-压力曲线出现峰值。设置轴向压力衰减至95%的峰值压力时停止并回车。记录峰值压力和回车后的试样端面校正半径。试验重复3次，依据式（4）计算得到σ分别为30.32，35.46和42.61 kPa，结果取平均值为36.13 kPa。

1.3 仿真参数设置

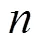
1.3.1 单轴密闭压缩仿真试验

单轴密闭压缩仿真试验中，选择颗粒-颗粒接触模型为EEPA模型，使用高300 mm（以保证以圆筒为颗粒工厂生成足够多的颗粒。实际试验中圆筒的高度为150 mm）、底部直径40 mm的圆柱模拟有机玻璃圆筒。仿真参数设置如表1所示。试验中土壤颗粒与限制壁之间黏性相比于土壤颗粒之间黏性较小，故不考虑限制壁与土壤颗粒黏性的影响，颗粒-接触部件模型选择Hertze-Mindlin (no slip) 模型。

表1 单轴密闭压缩仿真参数

Cleary[28]研究表明，无论颗粒间摩擦的角度如何，球形颗粒都不能代表“真实”固体，而非球形颗粒造成的颗粒群排列方式不同，可能导致试验数据的散射性较大。因此，单轴密闭压缩期间以圆筒为颗粒工厂，生成25 960个半径为1 mm的球形颗粒，以匹配与实际试验相同的初始填充质量。

仿真中对同一初始填充试样分别使用8（实际加载速率）、32.4和50 mm/s的加载速率（万能力学试验机能达到的加载速率范围为8～50 mm/s），发现3种加载速率下的试样应力-应变行为具有良好的一致性，如图4所示。此外，在50 mm/s的加载速率条件下，保持相同的仿真时间步长，较大k和组合下的单轴密闭压缩仿真试验容易发生穿模和崩溃。因此，为缩短仿真时间，单轴密闭压缩仿真试验的加载速率均为32.4 mm/s。

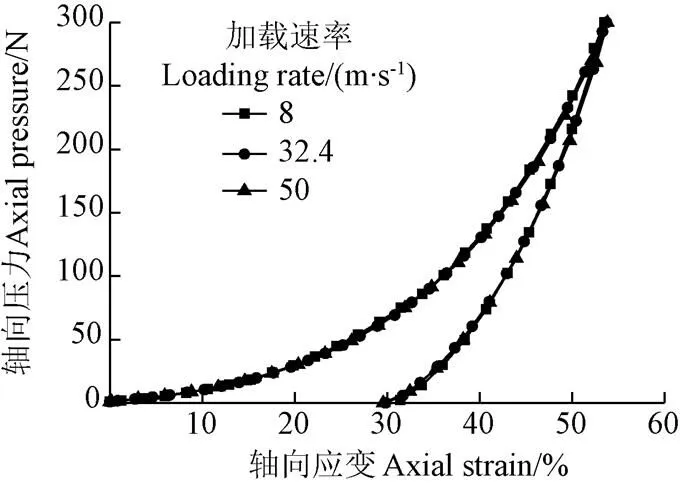
图4 不同加载速率下试样的轴向压力-轴向应变曲线

1.3.2 无侧限抗压强度仿真试验

单轴密闭压缩仿真试验结束后，去除限制壁，试样松弛0.2 s，以消除由于移除限制壁而增加的动能[18]。侧限移除将导致试样产生一定的径向膨胀加速度，为平衡径向加速度，防止无侧限抗压强度试验期间试样滑移出计算域，在去除限制壁之前，适当增加颗粒-几何体静摩擦系数至0.3。调整计算域高度以保留80 mm高度的试样，试样继续松弛0.2 s以消除由于部分颗粒移除而导致的动能变化。压盘以3.2 mm/s的恒定速率向下移动直至压力衰减至95%峰值压力，记录峰值压力和峰值压力时的校正半径，并根据式（4）计算σ。所有仿真试验的时间步长均为1×10-5s，Rayleigh时间步长约为6%。

2 参数标定试验与结果分析

根据EEPA模型可同时表征塑性和黏性的特点，利用塑性和黏性指标为响应值，依据仿真设置，通过Plackett-Burman试验筛选出与黏塑性显著相关的模型参数以减少参数标定试验因素。通过二次正交旋转组合试验，得到黏塑性指标与显著因素的回归模型，并求解与实测黏塑性指标对应的黏塑性参数。在标定黏塑性参数的基础上，通过二次正交旋转组合试验，得到弹性指标与待标定参数的回归模型，并求解与实测黏塑性指标和弹性指标对应的模型参数。

2.1 Plackett-Burman 试验

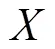
为从待标定参数中获取对ε和σ影响显著的参数，依据参数范围，以1个中心点估计试验随机误差和7个待标定参数为影响因素，以ε和σ为指标，Plackett-Burman仿真试验方案及结果如表2所示。

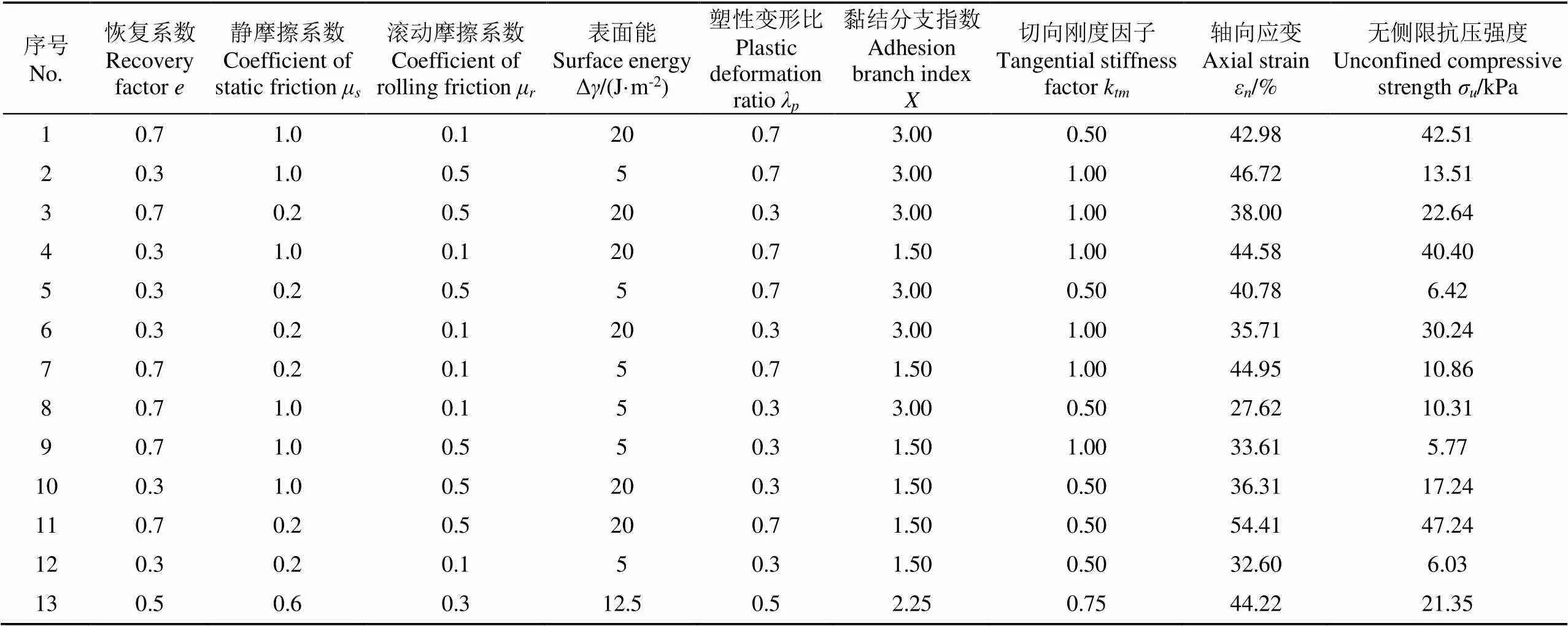
表2 Plackett-Burman试验方案与结果

对Plackett-Burman试验得到的ε和σ进行方差分析，以评价各参数对黏塑性指标的显著性。方差分析结果如表3所示。以置信度0.05与各因素值比较可知，λ对σ影响显著，Δ对σ影响极显著，λ对ε影响极显著，所以Δ和λ是影响土壤黏塑性的显著因素。

从表3可以看出，静摩擦系数μ的对σ和ε的值分别为0.695 7（>0.05）和0.804 7（>0.05），且当颗粒形状为球形时，静摩擦系数对单轴密闭压缩期间试样的应力-应变行为无显著影响[26]，说明μ在其试验范围（0.2～1）内对轴向压力-轴向应变曲线特征参数（，）、ε、σ均无显著影响。因此后续试验将μ取中间值0.6。

2.2 黏塑性参数标定结果与分析

为标定与实测黏塑性指标（σ和ε）对应的Δ和λ，基于Plackett-Burman试验因素范围，依据二次正交旋转组合试验原理，以3个中心点、2个因素（Δ和λ）、2个指标（σ和ε）进行二次正交旋转组合试验，试验因素水平如表4所示，试验方案和结果如表5所示。仿真试验中对黏塑性影响不显著的其他参数均取Plackett-Burman试验因素范围中间值，具体为：=0.5、μ=0.6、μ=0.3、=2.25，k=0.75。

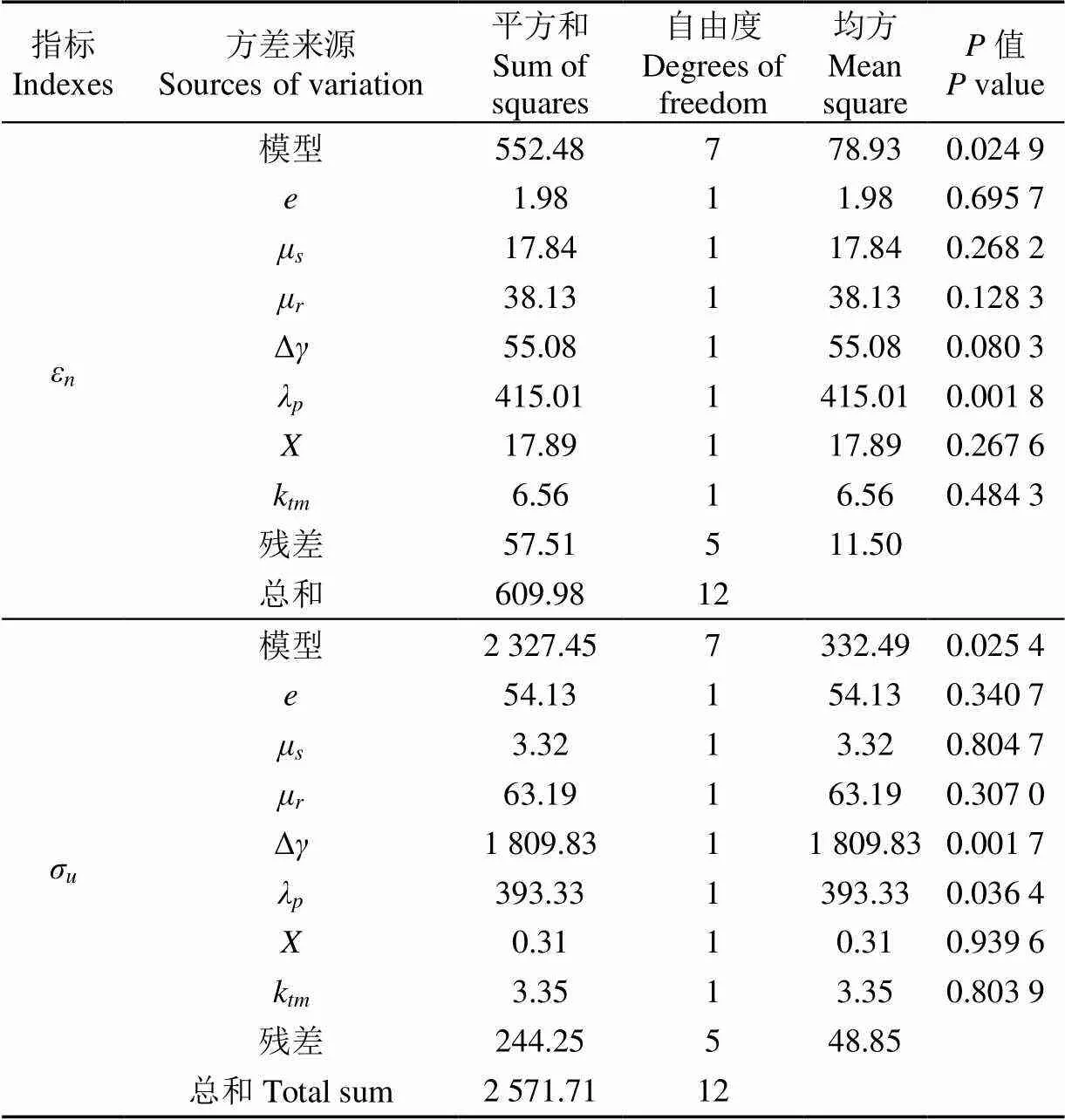
表3 εn和σu的方差分析

注：<0.01表示极显著，0.01≤<0.05表示显著，≥0.05表示不显著。下同。

Note:<0.01 means extremely significant, 0.01≤<0.05 means significant,≥0.05 means insignificant. The same as below.

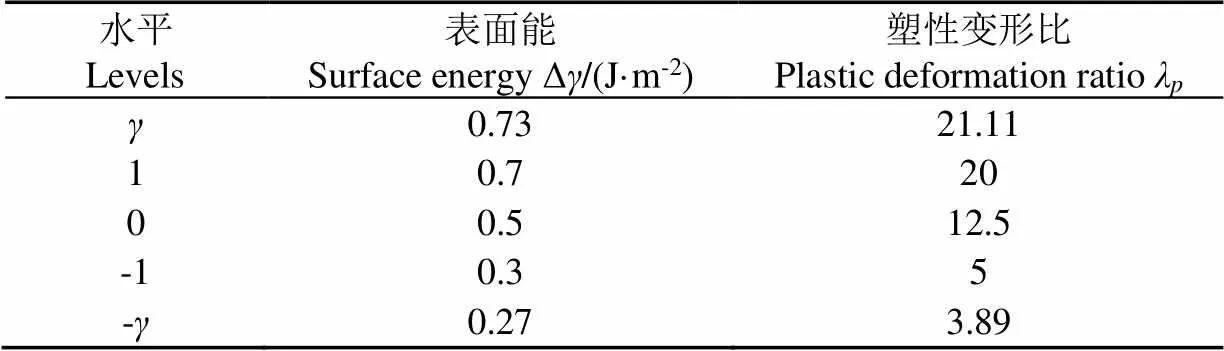
表4 Δγ和λp二次正交旋转组合试验因素水平编码表

根据表5，利用Design Expert 8.0.5得到以下2个回归方程：

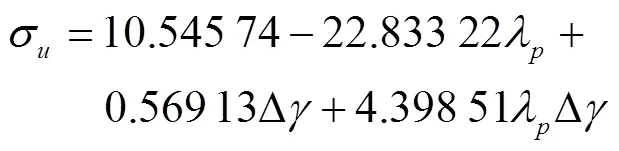
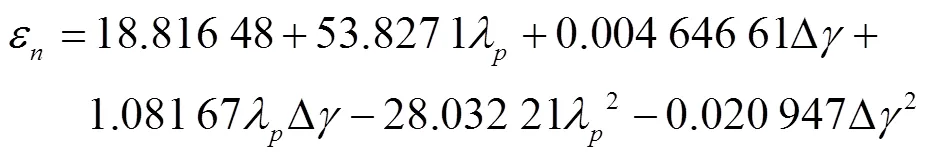
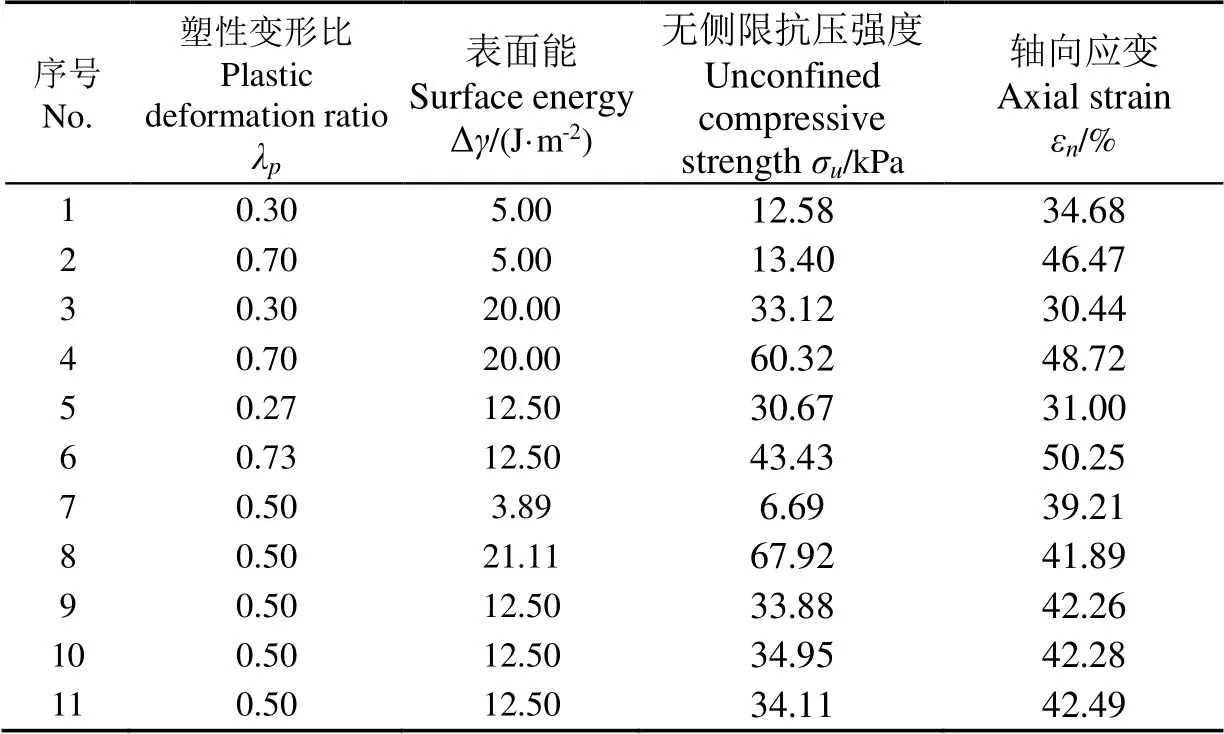
表5 Δγ和λp的二次正交旋转组合试验方案及结果

为验证所得ε和σ与Δ和λ关系模型的可靠性，进行3组验证试验。结果表明，ε的预测值与实测值的平均误差约为0.77%，标准差约为1.27%；σ的预测值与实测值的平均误差约为1.20%，标准差约为10.59%。所得模型可准确且稳定预测试样轴向应变ε，可准确预测σ但稳定性略差。

将式（5）和式（6）联立求解，得到与σ和ε对应的Δ和λ分别为15.6 J/m2和0.36。

2.3 弹性参数标定结果与分析

为减少与实测弹性指标（，）对应的弹性参数、μ、、k的解的数量，同时将黏弹塑性指标作为评价指标，以3个中心点、4个因素（、μ、和k）设计二次正交旋转组合试验，星号臂长1.546 71，因素水平如表6所示。将加载阶段试样的轴向压力-轴向应变数据与式（2）拟合，试验结果如表7所示。

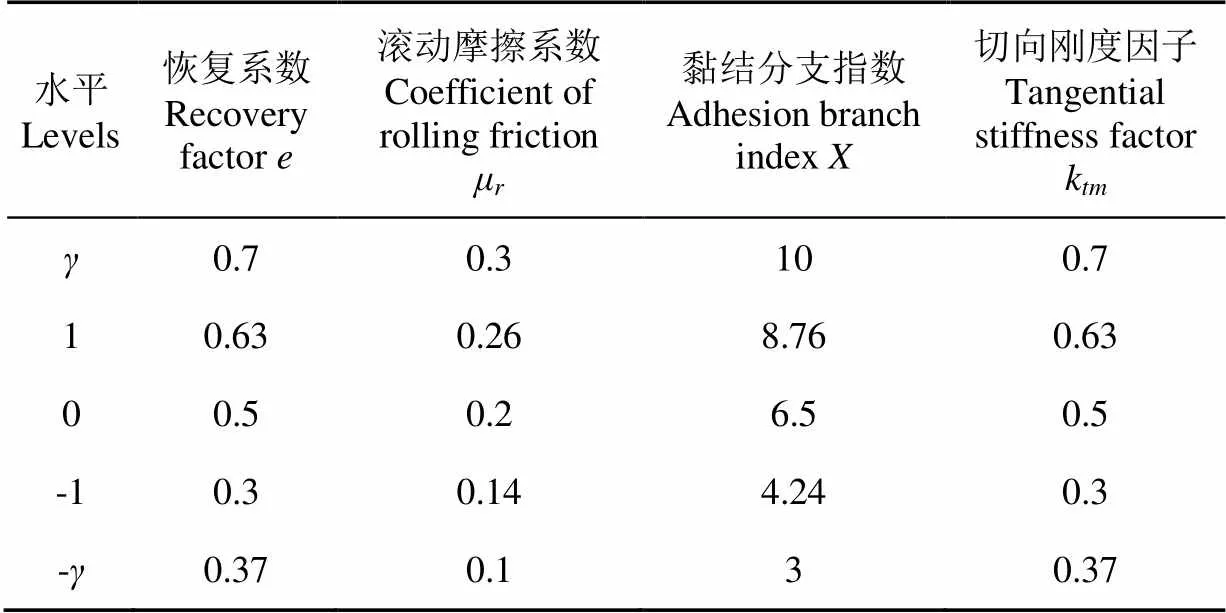
表6 弹性参数的二次正交旋转组合试验因素水平编码表

根据表7，利用Design Expert 8.0.5软件，保留不显著项的条件下得到以下4个回归方程：

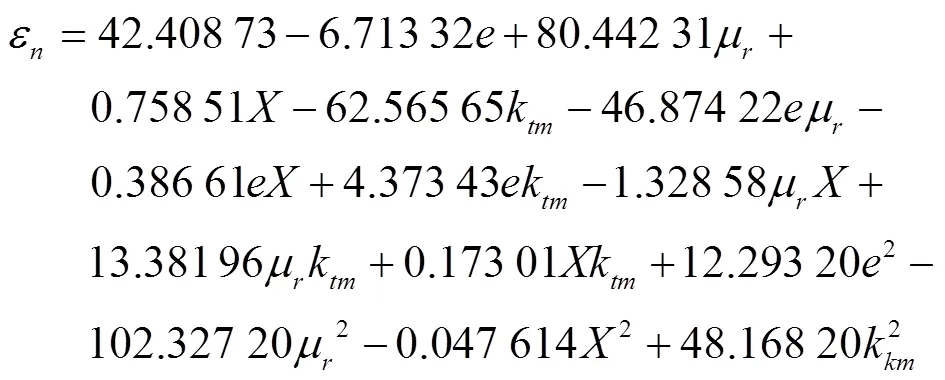
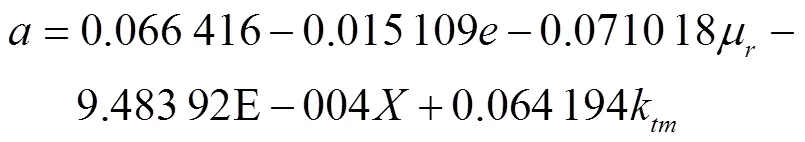
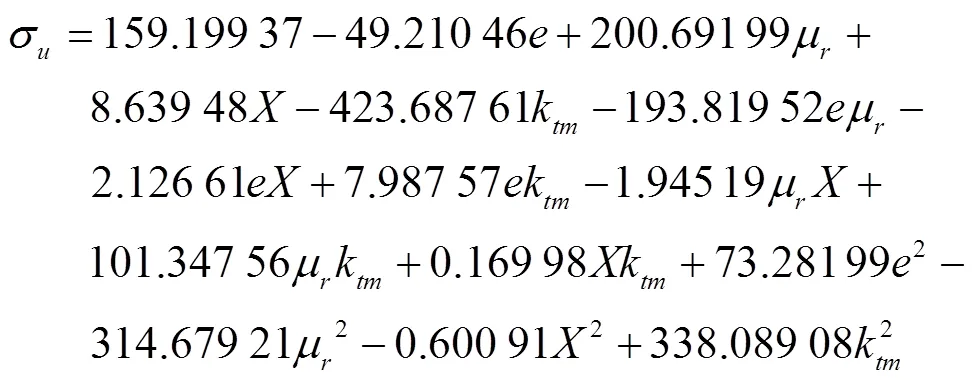
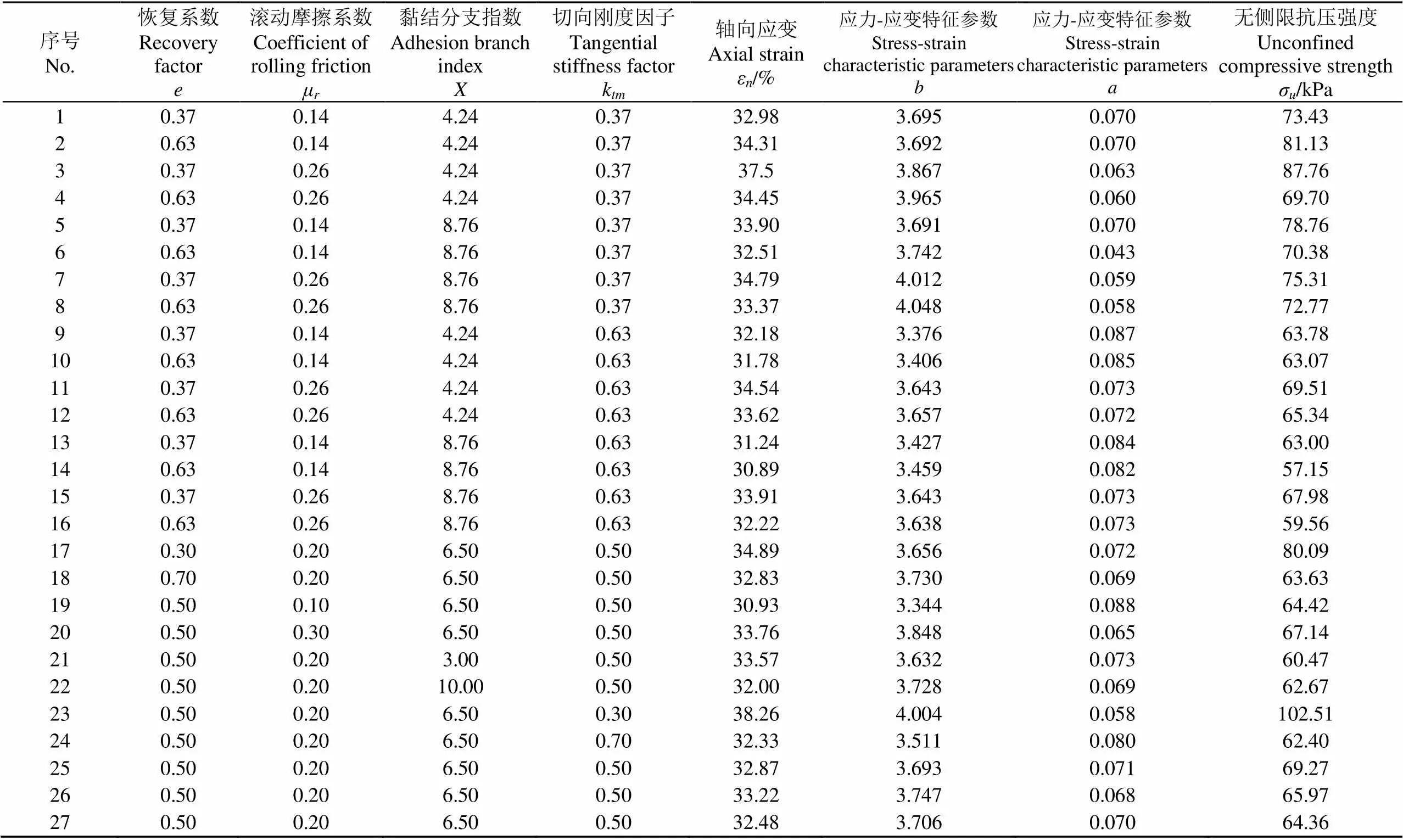
表7 e,μr, X和ktm的二次正交旋转组合试验方案及结果

对得到的ε、σ、和进行方差分析，结果如表8所示。根据表8，ε、σ、、的模型值分别为0.001 1（<0.01）、0.005 9（<0.01）、<0.000 1（<0.01）和<0.000 1（<0.01），说明标定弹性参数的各指标拟合模型均极显著，拟合模型能够准确描述因变量与自变量之间的关系。切向刚度因子k对ε、σ、、的值均为<0.000 1（<0.01），且k二次项对ε、σ影响极显著。

以实测的ε、σ、和为目标对式（7）～（10）方程组求解，获得27组解。这些解几乎无差异，以Desirability值为参考，选择一组Desirability值最接近1（可靠度最高）的参数=0.37、μ=0.26、=4.24和k=0.52。

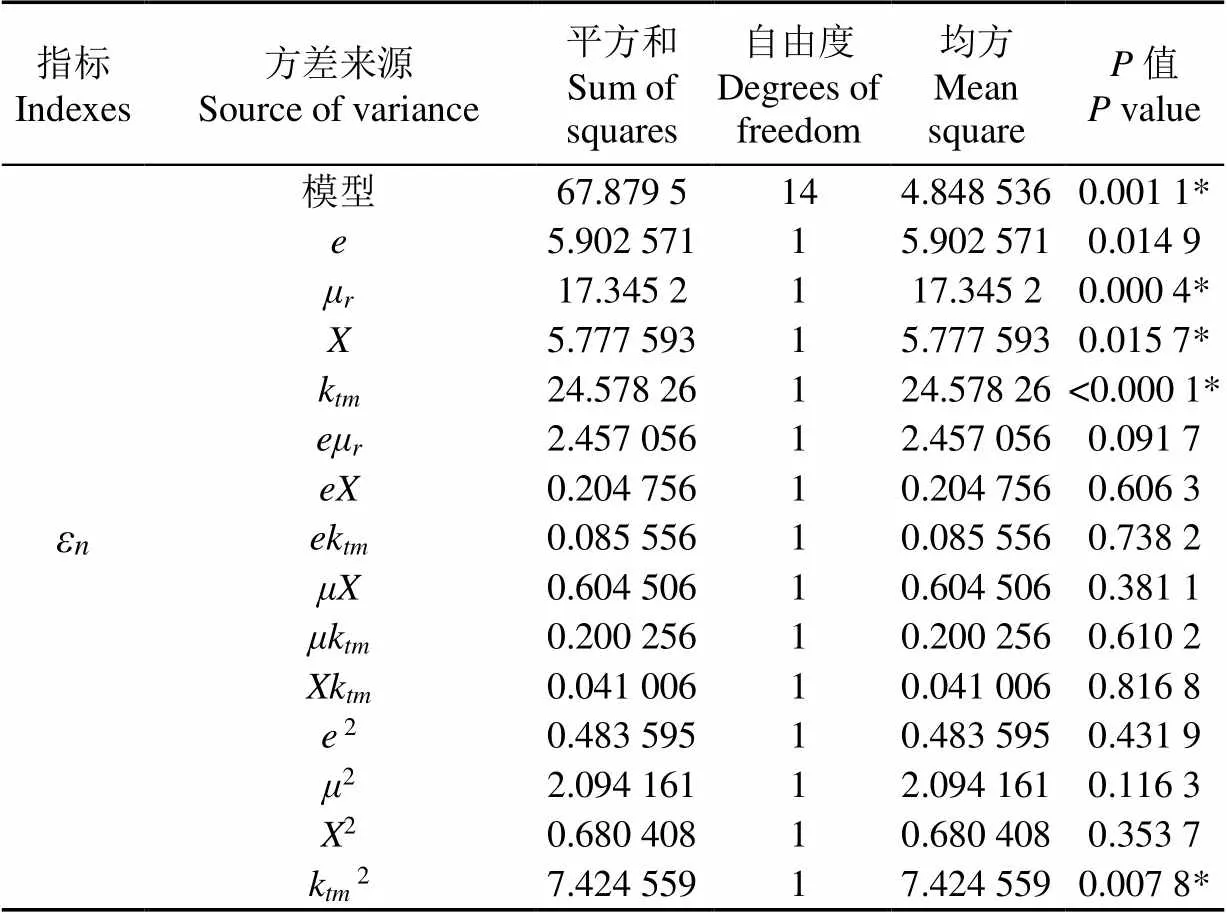
表8 黏弹塑性指标方差分析

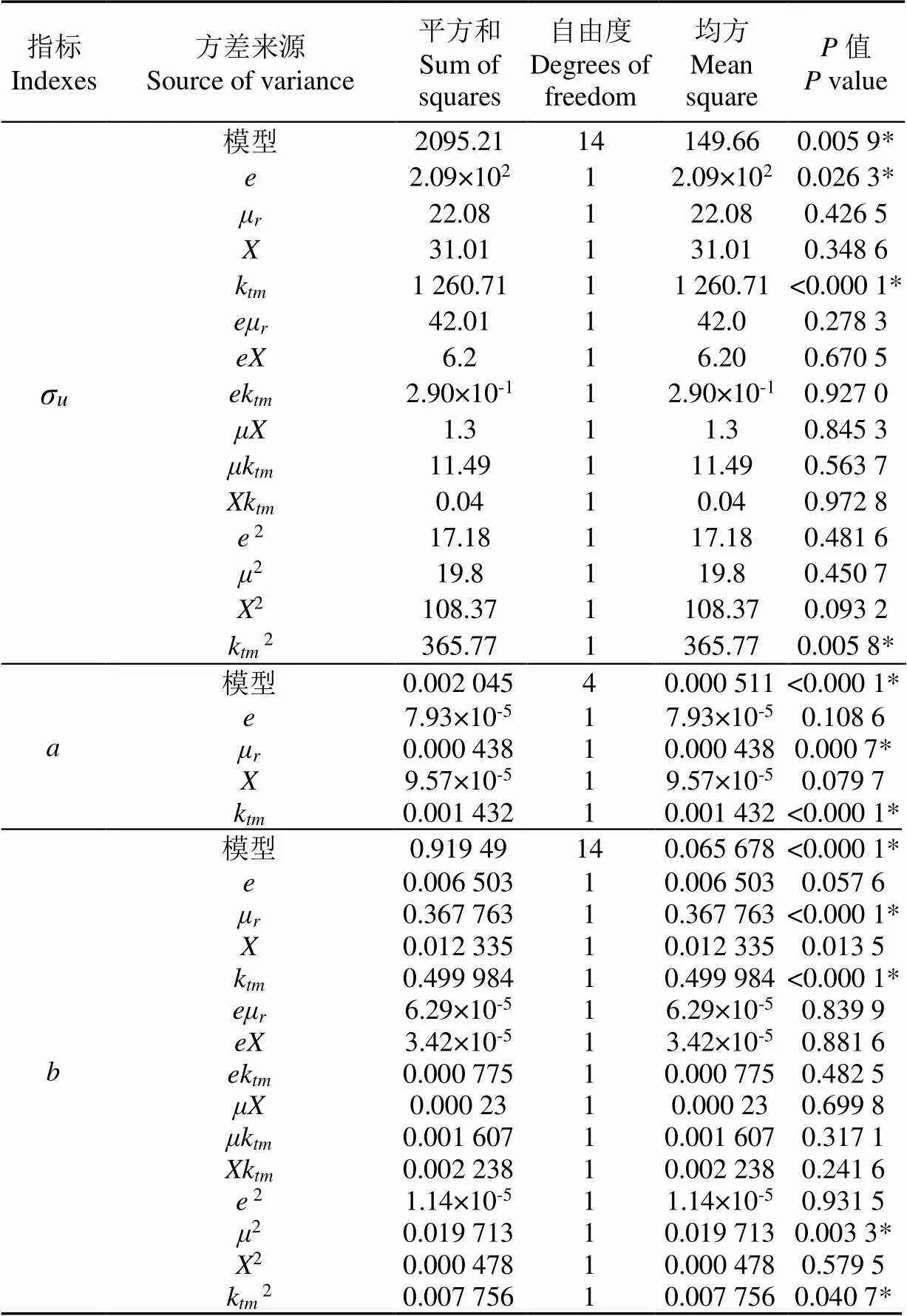
续表

3 标定结果验证

根据黏塑性参数和弹性参数标定结果，利用EDEM_v2018软件建立离散元仿真模型，进行单轴密闭压缩仿真试验和无侧限抗压强度仿真试验，以验证标定结果的可信度。试验重复3次，结果如表9所示。

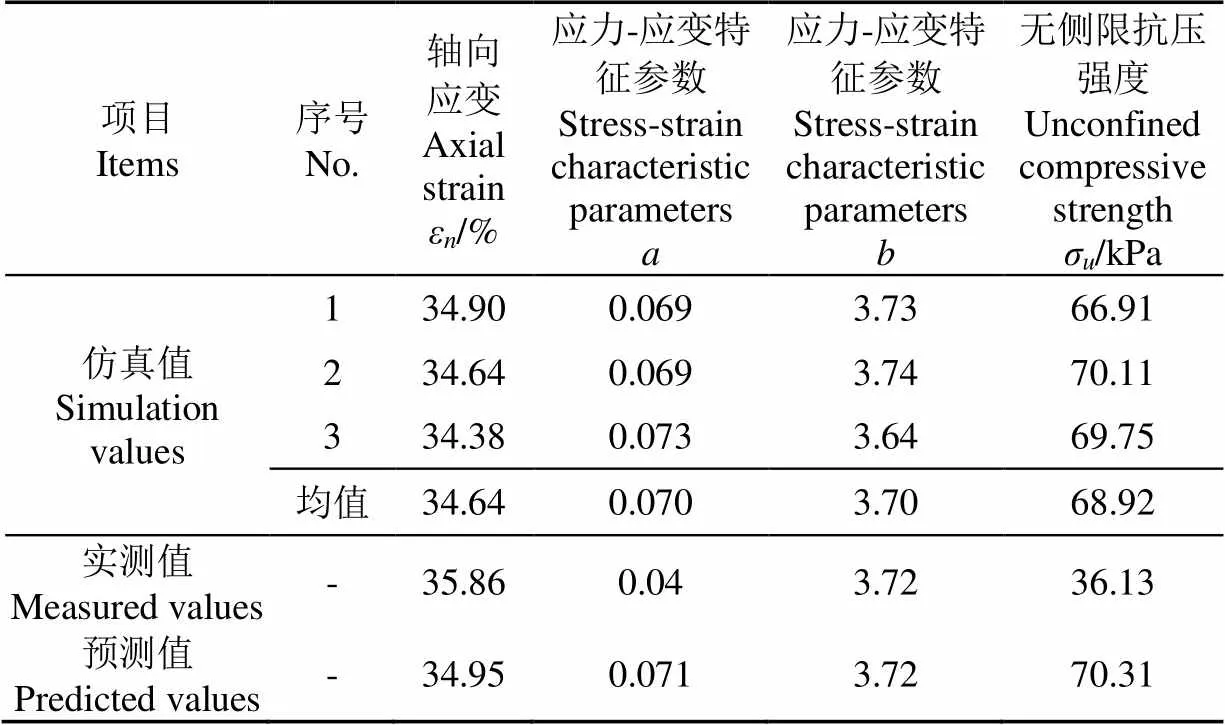
表9 单轴密闭压缩和无侧限抗压强度验证试验结果

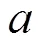
将表9中第一组单轴密闭压缩仿真试验的轴向压力-轴向应变曲线与实测的土壤轴向压力-轴向应变曲线对比，如图5所示。利用Orign Pro8.5软件，将仿真值与实测值对轴向应变积分求差，取其相对轴向应变的平均值，得到仿真轴向压力与实测值平均误差约为1.95 N。积分差值相对实测值积分误差约为3.3%。故可以认为，在3%～45%的轴向应变内仿真试样的应力-应变行为与实际情况基本一致。

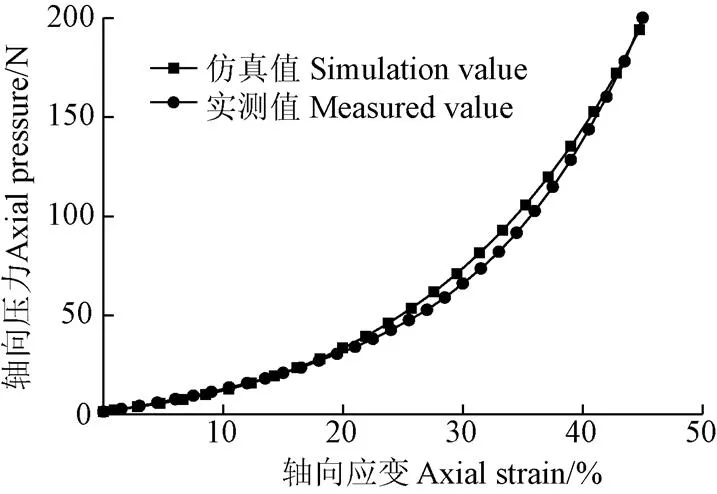
图5 标定区间的应力-应变曲线对比

4 结 论

本研究通过Plackett-Burman试验和Central Composite试验标定了EEPA模型参数。结合标定试验与验证试验结果与分析，主要结论如下：

1）Plackett-Burman试验结果表明，模型参数中的塑性变形比对轴向应变影响极显著，对无侧限抗压强度影响显著；表面能对无侧限抗压强度影响极显著。

2）参数标定试验结果表明，轴向应变、无侧限抗压强度关于黏塑性参数的拟合模型均显著。轴向应变、无侧限抗压强度、曲线特征参数关于弹性参数的拟合模型均极显著。对回归模型求解，得到与实测值对应的表面能、塑性变形比、恢复系数、滚动摩擦系数、黏结分支指数、切向刚度因子分别为15.6 J/m2、0.36、0.37、0.26、4.24、0.52。

3）标定结果验证试验结果表明，轴向应变、曲线特征参数的仿真值与实测值的相对误差分别为-3.40%和0.54%，轴向压力仿真值与实测值误差为1.95 N，与实测值积分差值相对误差为3.3%。无侧限抗压强度、曲线特征参数与实测值的差异略大。

对土壤黏塑性指标影响显著的因素不只是表面能和塑性变形比，切向刚度因子对其影响也较大，因而造成标定结果的验证试验中，无侧限抗压强度的仿真值与实测值存在较大差异，后续研究应在Plackett-Burman试验前通过单因素试验确定切向刚度因子的取值范围。

[1] Coetzee C J, Lombard S G. The destemming of grapes: Experiments and discrete element modelling[J]. Biosystems Engineering, 2013, 114(3): 232-248.

[2] Yu Y, Fu H, Yu J. DEM-based simulation of the corn threshing process[J]. Advanced Powder Technology, 2015, 26(5): 1400-1409.

[3] 王立军，冯鑫，郑招辉，等. 玉米清选组合孔筛体设计与试验[J]. 农业机械学报，2019，50(5)：104-113.

Wang Lijun, Feng Xin, Zheng Zhaohui, et al. Design and test of combined sieve of maize screening[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(5): 104-113. (in Chinese with English abstract)

[4] 王立军，武振超，冯鑫，等. 玉米收获机清选曲面筛设计与试验[J]. 农业机械学报，2019，50(2)：90-101.

Wang Lijun, Wu Zhenchao, Feng Xin, et al. Design and experiment of curved screen for maize grain harvester[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(2): 90-101. (in Chinese with English abstract)

[5] 王立军，张传根，丁振军. 玉米收获机清选筛体结构优化[J]. 农业机械学报，2016，47(9)：108-114.

Wang Lijun, Zhang Chuangen, Ding Zhenjun. Structure optimization of cleaning screen for maize harvester[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(9): 108-114. (in Chinese with English abstract)

[6] 赵淑红，刘宏俊，谭贺文，等. 仿旗鱼头部曲线型开沟器设计与性能试验[J]. 农业工程学报，2017，33(5)：32-39.

Zhao Shuhong, Liu Hongjun, Tan Hewen, et al. Design and performance experiment of opener based on bionic sailfish head curve[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(5): 32-39. (in Chinese with English abstract)

[7] 郑侃，何进，李洪文，等. 基于离散元深松土壤模型的折线破土刃深松铲研究[J]. 农业机械学报，2016，47(9)：62-72.

Zheng Kan, He Jin, Li Hongwen, et al. Research on polyline soil-breaking blade subsoiler based on subsoiling soil model using discrete element method[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(9): 62-72. (in Chinese with English abstract)

[8] 张锐，李建桥，周长海，等. 推土板表面形态对土壤动态行为影响的离散元模拟[J]. 农业工程学报，2007，23(9)：13-19.

Zhang Rui, Li Jianqiao, Zhou Changhai, et al. Simulation of dynamic behavior of soil ahead of the bulldozing plates with different surface configurations by discrete element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2007, 23(9): 13-19. (in Chinese with English abstract)

[9] 于建群，钱立彬，于文静，等. 开沟器工作阻力的离散元法仿真分析[J]. 农业机械学报，2009，40(6)：53-57.

Yu Jianqun, Qian Libin, Yu Wenjing, et al. DEM Analysis of the resistances applied on furrow openers[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(6): 53-57. (in Chinese with English abstract)

[10] 马跃进，王安，赵建国，等. 基于离散元法的凸圆刃式深松铲减阻效果仿真分析与试验[J]. 农业工程学报，2019，35(3)：16-23.

Ma Yuejin, Wang An, Zhao Jianguo, et al. Simulation analysis and experiment of drag reduction effect of convex blade subsoiler based on discrete element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(3): 16-23. (in Chinese with English abstract)

[11] Ucgul M, Fielke J M, Saunders C. 3D DEM tillage simulation: Validation of a hysteretic spring (plastic) contact model for a sweep tool operating in a cohesionless soil[J]. Soil and Tillage Research, 2014, 144: 220-227.

[12] Bravo E L, Tijskens E, Suarez M H, et al. Prediction model for non-inversion soil tillage implemented on discrete element method[J]. Comput. Electron. Agric, 2014, 106: 120-127.

[13] Chen Y, Munkholm L J, Nyord T. A discrete element model for soil-sweep interaction in three different soils[J]. Soil and Tillage Research, 2013, 126: 34-41.

[14] Li B, Chen Y, Chen J. Modeling of soil–claw interaction using the discrete element method (DEM)[J]. Soil and Tillage Research, 2016, 158: 177-185.

[15] Katterfeld A, Wensrich C. Understanding granular media: from fundamentals and simulations to industrial application[J]. Granular Matter, 2017, 19(4).

[16] Roessler T, Richter C, Katterfeld A, et al. Development of a standard calibration procedure for the DEM parameters of cohesionless bulk materials-part I: Solving the problem of ambiguous parameter combinations[J]. Powder Technology, 2019, 343: 803-812.

[17] Karkala S, Davis N, Wassgren C, et al. Calibration of discrete- element-method parameters for cohesive materials using dynamic-yield-strength and shear-cell experiments[J]. Processes, 2019, 7(5): 278.

[18] Janda A, Ooi J Y. DEM modeling of cone penetration and unconfined compression in cohesive solids[J]. Powder Technology, 2016, 293: 60-68.

[19] 王宪良，胡红，王庆杰，等. 基于离散元的土壤模型参数标定方法[J]. 农业机械学报，2017，48(12)：78-85.

Wang Xianliang, Hu Hong, Wang Qingjie, et al. Calibration method of soil contact characteristic parameters based on DEM theory[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(12): 78-85. (in Chinese with English abstract)

[20] Xia R, Li B, Wang X, et al. Measurement and calibration of the discrete element parameters of wet bulk coal[J]. Measurement, 2019, 142: 94-95.

[21] Ucgul M, Fielke J M, Saunders C. Three-dimensional discrete element modelling of tillage: Determination of a suitable contact model and parameters for a cohesionless soil[J]. Biosystems Engineering, 2014, 121:105-117.

[22] Barrios G K P, Carvalho R M, Kwade A, et al. Contact parameter estimation for DEM simulation of iron ore pellet handling[J]. Powder Technology, 2013, 248:84-93.

[23] Coetzee C. Calibration of the discrete element method and the effect of particle shape[J]. Powder Technol, 2016, 297: 50-70.

[24] Ucgul M, Fielke J M, Saunders C. Three-dimensional discrete element modelling (DEM) of tillage: Accounting for soil cohesion and adhesion[J]. Biosystems Engineering, 2015, 129: 298-306.

[25] 李俊伟，佟金，胡斌，等. 不同含水率黏重黑土与触土部件互作的离散元仿真参数标定[J]. 农业工程学报，2019，35(6)：130-140.

Li Junwei, Tong Jin, Hu Bin, et al. Calibration of parameters of interaction between clayey black soil with different moisture content and soil-engaging component in northeast China[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(6): 130-140.

[26] Thakur S C, Morrissey J P, Sun J, et al. Micromechanical analysis of cohesive granular materials using the discrete element method with an adhesive elasto-plastic contact model[J]. Granular Matter, 2014, 16(3): 383-400.

[27] Tomas J. Adhesion of ultrafine particles: A micromechanical approach[J]. Chemical Engineering Science, 2007, 62(7): 1997-2010.

[28] Cleary P W. DEM prediction of industrial and geophysical particle flows[J]. Particuology, 2010, 8(2): 106-118.

Calibration of discrete element parameters of soils based on unconfined compressive strength test

Xie Fangping1,2, Wu Zhengyang1, Wang Xiushan1,2, Liu Dawei1,2, Wu Bei1,2, Zhang Zhengzhong1

(1.,410128,;2.410128,)

In order to calibrate the discrete element parameters of viscoplastic soil based on the Edinburgh Elasto-Plastic Adhesion (EEPA) model, two constants to describe the stress-strain behavior of the sample soils were defined in this study. The axial strain of the soil under a load of 300 kPa was used to characterize the plasticity of the soil in the uniaxial closed compression test. First, two EEPA model parameters based on the physical properties of the soil and other scholars’ research were determined, i.e. the constant pull-off force and the load branch index. Then, another two factors, surface energy and plastic deformation ratio, that had significant effects on axial strain and unconfined compressive strength based on the Plackett-Burman test results were described. Next, the central composite test based on the response surface method was designed, and the two factors that matched the actual measured axial strain and unconfined compressive strength based on the test results were determined.According to the test results. the four discrete element parameters corresponding to the two measured constants, unconfined compressive strength and axial strain were solved. Finally, the soil discrete element parameters were calibrated based on the EEPA model,and those were that plastic deformation ratio of 0.36, surface energy of 15.6 J/m2, static friction coefficient of 0.6, rolling friction coefficient of 0.26, recovery coefficient of 0.37, adhesion branch index of 4.24 and tangential stiffness factor of 0.52.Verification test results showed that the EEPA model parameters calibrated based on the response surface method could simulate the plastic deformation of the sample soil under a load of 300 kPa and the stress-strain behavior within 3%-45% of the axial strain. In addition, the results of Quadratic orthogonal rotation combined test were analyzedand it showed that the tangential stiffness factor was one of the key parameters affecting axial strain and unconfined compressive strength, and the random error of the unconfined compressive strength simulation test was also one of the reasons. Moreover, it was found that the limit of the value range of the tangential stiffness factor was the cause of the huge difference between the simulation and the measured values of the unconfined compressive strength.

soils;stress; strain;discrete element method; calibration; plastic deformation; unconfined compressive strength

谢方平，吴正阳，王修善，等. 基于无侧限抗压强度试验的土壤离散元参数标定[J]. 农业工程学报，2020，36(13)：39-47.doi：10.11975/j.issn.1002-6819.2020.13.005 http://www.tcsae.org

Xie Fangping, Wu Zhengyang, Wang Xiushan, et al. Calibration of discrete element parameters of soils based on unconfined compressive strength test[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(13): 39-47. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.13.005 http://www.tcsae.org

2019-12-18

2020-06-07

湖南省农机装备创新发展项目（湘财农指（2018）175号）

谢方平，教授，主要从事农业机械性能试验与创新设计。Email：hunanxie2002@163.com

10.11975/j.issn.1002-6819.2020.13.005

O347.7

A

1002-6819(2020)-13-0039-09